初中一对一精品辅导讲义:正弦定理与余弦定理
- 格式:docx
- 大小:386.61 KB
- 文档页数:8

此为三角函数最为基础的知识,在以后的多学科学习中都能用到,需要学生熟练掌握,并灵活运用。
解三角形【考点及要求】 1. 掌握正弦定理、余弦定理; 2. 并能初步应用正弦定理、余弦定理解决三角形中的有关问题. 【基础知识】在C B A c b a ABC ∠∠∠∆、、分别是、、中,所对的边,ABC R ∆为的外接圆半径,则有,1.正弦定理:R CcB b A a 2sin sin sin =∠=∠=∠; 2.余弦定理:bca cb A 2cos 222-+=A bc c b a cos 2222-+=⇔ ac b c aB 2cos 222-+=B ac c a b cos 2222-+=⇔ abc b a C 2cos 222-+=C ab b a c cos 2222-+=⇔ 3.常用公式:(1)π=++C B A ;(2)B ac A bc C ab S sin 21cos 21sin 21===知识点一:解直角三角形【典型例题讲练】例1 在ΔABC 中,已知a=3,b=2,B=45°,求A,C 及边c .【变式训练】 1.在△ABC 中,已知a=3,b=2,B=45°,求A 、C 和c.知识点二:正、余弦定理的运用【典例精析】 例1、(2010辽宁文数)在ABC ∆中,a b c 、、分别为内角A B C 、、的对边,且2sin (2)sin (2)sin a A b c B c b C =+++. (Ⅰ)求A 的大小;(Ⅱ)若sin sin 1B C +=,试判断ABC ∆的形状.例2、(2010重庆文数)设ABC ∆的内角A 、B 、C 的对边长分别为a 、b 、c,且32b +32c -32a =42bc . (Ⅰ) 求sinA 的值;(Ⅱ)求2sin()sin()441cos 2A B C Aππ+++-的值.例3、在△ABC 中,a 、b 、c 分别是角A ,B ,C 的对边,且CB cos cos =-ca b +2.(1)求角B 的大小; (2)若b=13,a+c=4,求△ABC 的面积.例4、在△ABC中,角A、B、C的对边分别为a、b、c,已知a+b=5,c=7,且4sin22BA+-cos2C=27.(1)求角C的大小;(2)求△ABC的面积.【变式训练】1.(2010天津文数)在∆ABC中,coscosAC B AB C=。

第一课时 正弦定理与余弦定理知识点梳理1、ABC ∆中,45,60,10,A B a === 则b 等于( )A 52B 102 C1063D 56 2、在△ABC 中,已知8=a ,B=060,C=075,则b 等于A.64B.54C.34D.322 3、已知ABC ∆中,c b a 、、分别是角C B A 、、的对边, 60,3,2===B b a ,则A = A. 135 B. 45 C. 135或 45 D.904、在△ABC 中,a b c 、、分别是三内角A B C 、、的对边, ︒=︒=45,75C A ,2b =,则此三角形的最小边长为( )A .46 B .322 C .362 D . 425、在中,B=,C=,c=1,则最短边长为( ) A .B .C .D .ABC ∆30︒45︒63221232课前检测正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即sin sin a b A B =sin cC=(1)正弦定理说明同一三角形中,边与其对角的正弦成正比,且比例系数为同一正数,即存在正数k 使sin a k A =,sin b k B =,sin c k C =;(2)sin sin a b A B =sin c C =等价于sin sin a b A B =,sin sin c b C B =,sin a A =sin cC从而知正弦定理的基本作用为:①已知三角形的任意两角及其一边可以求其他边,如sin sin b Aa B=; ②已知三角形的任意两边与其中一边的对角可以求其他角的正弦值,如sin sin aA B b=。
一般地,已知三角形的某些边和角,求其他的边和角的过程叫作解三角形。
例题 .在ABC ∆中,已知3=a , 2=b , B=450.求A 、C 和c. 解:004590B =< 且 ,b a <∴A 有两解.由正弦定理,得23245sin 3sin sin 0=∙==b B a A 0012060==∴A A 或 1) 当A=600时,C=1800-A-B=75, 00sin 2sin 7562sin 2sin 45b Cc B+===2) 当A=1200时,C=1800-A-B=150, 0sin 2sin1562sin 2sin 45b C c B -===(1)定理的表示形式:sin sin abAB=sin cC==()0sin sin sin a b ck k A B C++=>++;或sin a k A =,sin b k B =,sin c k C =(0)k >(2)正弦定理的应用范围:①已知两角和任一边,求其它两边及一角; ②已知两边和其中一边对角,求另一边的对角。


第一课时 1.1.1 正弦定理教学要求:通过对任意三角形边长和角度关系的探索,掌握正弦定理的内容及其证明方法;会运用正弦定理与三角形内角和定理解斜三角形的两类基本问题.教学重点:正弦定理的探索和证明及其基本应用.教学难点:已知两边和其中一边的对角解三角形时判断解的个数. 教学过程:一、复习准备:1. 讨论:在直角三角形中,边角关系有哪些?(三角形内角和定理、勾股定理、锐角三角函数)如何解直角三角形?那么斜三角形怎么办?2. 由已知的边和角求出未知的边和角,称为解三角形. 已学习过任意三角形的哪些边角关系?(内角和、大边对大角) 是否可以把边、角关系准确量化? →引入课题:正弦定理 二、讲授新课:1. 教学正弦定理的推导:①特殊情况:直角三角形中的正弦定理: sin A =ca sin B =cb sin C =1 即c =sin sin sin a b cA B C==. ② 能否推广到斜三角形? (先研究锐角三角形,再探究钝角三角形) 当∆ABC 是锐角三角形时,设边AB 上的高是CD ,根据三角函数的定义,有sin sin CD a B b A ==,则sin sin a bA B=. 同理,sin sin a cA C=(思考如何作高?),从而sin sin sin a b cA B C==. ③*其它证法:证明一:(等积法)在任意斜△ABC 当中S △ABC =111sin sin sin 222ab C ac B bc A ==. 两边同除以12abc 即得:sin a A =sin bB =sin c C.证明二:(外接圆法)如图所示,∠A =∠D ,∴2sin sin a a CD R A D===, 同理sin bB=2R ,sin c C =2R .证明三:(向量法)过A 作单位向量j 垂直于AC ,由AC +CB =AB 边同乘以单位向量j 得…..④ 正弦定理的文字语言、符号语言,及基本应用:已知三角形的任意两角及其一边可以求其他边;已知三角形的任意两边与其中一边的对角可以求其他角的正弦值. 2. 教学例题:① 出示例1:在∆ABC 中,已知045A =,060B =,42a =cm ,解三角形.分析已知条件 → 讨论如何利用边角关系 → 示范格式 → 小结:已知两角一边② 出示例2:045,2,,ABC c A a b B C ∆===中,求和.分析已知条件 → 讨论如何利用边角关系 → 示范格式 → 小结:已知两边及一边对角③练习:060,1,,ABC b B c a A C ∆===中,求和.在∆ABC 中,已知10a =cm ,14b =cm ,040=A ,解三角形(角度精确到01,边长精确到1cm )④ 讨论:已知两边和其中一边的对角解三角形时,如何判断解的数量? 3. 小结:正弦定理的探索过程;正弦定理的两类应用;已知两边及一边对角的讨论.三、巩固练习:1.已知∆ABC 中,∠A =60°,a =,求sin sin sin a b cA B C++++.2. 作业:教材P5 练习1 (2),2题. 第二课时 1.1.2 余弦定理(一)教学要求:掌握余弦定理的两种表示形式及证明余弦定理的向量方法,并会运用余弦定理解决两类基本的解三角形问题.教学重点:余弦定理的发现和证明过程及其基本应用. 教学难点:向量方法证明余弦定理. 教学过程:一、复习准备:1. 提问:正弦定理的文字语言? 符号语言?基本应用?2. 练习:在△ABC 中,已知10c =,A =45︒,C =30︒,解此三角形. →变式3. 讨论:已知两边及夹角,如何求出此角的对边? 二、讲授新课:1. 教学余弦定理的推导:① 如图在ABC ∆中,AB 、BC 、CA 的长分别为c 、a 、b .∵AC AB BC =+,∴()()AC AC AB BC AB BC •=+•+222AB AB BC BC =+•+222||||cos(180)AB AB BC B BC =+•-+222cos c ac B a =-+.即2222cos b c a ac B =+-,→② 试证:2222cos a b c bc A =+-,2222cos c a b ab C =+-.③ 提出余弦定理:三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.用符号语言表示2222cos a b c bc A =+-,…等; → 基本应用:已知两边及夹角④ 讨论:已知三边,如何求三角? →余弦定理的推论:222cos 2b c a A bc+-=,…等.⑤ 思考:勾股定理与余弦定理之间的关系? 2. 教学例题:① 出示例1:在∆ABC 中,已知=a c 060=B ,求b 及A . 分析已知条件 → 讨论如何利用边角关系 → 示范求b→ 讨论:如何求A ?(两种方法) (答案:b =060A =) → 小结:已知两边及夹角②在∆ABC 中,已知13a cm =,8b cm =,16c cm =,解三角形.分析已知条件 → 讨论如何利用边角关系 → 分三组练习 → 小结:已知两角一边 3. 练习:① 在ΔABC 中,已知a =7,b =10,c =6,求A 、B 和C .② 在ΔABC 中,已知a =2,b =3,C =82°,解这个三角形.4. 小结:余弦定理是任何三角形边角之间存在的共同规律,勾股定理是余弦定理的特例;余弦定理的应用范围:①已知三边求三角;②已知两边及它们的夹角,求第三边.三、巩固练习:1. 在∆ABC 中,若222a b c bc =++,求角A . (答案:A =1200)2. 三角形ABC 中,A =120°,b =3,c =5,解三角形. → 变式:求sin B sin C ;sin B +sin C .3. 作业:教材P8 练习1、2(1)题.第三课时 1.1 正弦定理和余弦定理(练习)教学要求:进一步熟悉正、余弦定理内容,能熟练运用余弦定理、正弦定理解答有关问题,如判断三角形的形状,证明三角形中的三角恒等式. 教学重点:熟练运用定理.教学难点:应用正、余弦定理进行边角关系的相互转化.教学过程:一、复习准备:1. 写出正弦定理、余弦定理及推论等公式.2. 讨论各公式所求解的三角形类型. 二、讲授新课:1. 教学三角形的解的讨论:① 出示例1:在△ABC 中,已知下列条件,解三角形.(i ) A =6π,a =25,b =; (ii ) A =6π,a =,b =; (iii ) A =6π,ab =; (iiii ) A =6π,a =50,b =.分两组练习→ 讨论:解的个数情况为何会发生变化? ② 用如下图示分析解的情况. (A 为锐角时)已知边a,b 和∠A有两个解仅有一个解无解CH=bsinA<a<b a=CH=bsinAa<CH=bsinA② 练习:在△ABC 中,已知下列条件,判断三角形的解的情况. (i ) A =23π,a =25,b =; (ii ) A =23π,a =25,b =2. 教学正弦定理与余弦定理的活用:① 出示例2:在△ABC 中,已知sin A ∶sin B ∶sin C =6∶5∶4,求最大角的余弦.分析:已知条件可以如何转化?→ 引入参数k ,设三边后利用余弦定理求角.② 出示例3:在ΔABC 中,已知a =7,b =10,c =6,判断三角形的类型.分析:由三角形的什么知识可以判别? → 求最大角余弦,由符号进行判断结论:活用余弦定理,得到:=+⇔⇔∆>+⇔⇔∆<+⇔⇔222222222是直角是直角三角形是钝角是钝角三角形是锐角a b c A ABC a b c A ABC a b c A ∆是锐角三角形ABC③ 出示例4:已知△ABC 中,cos cos b C c B =,试判断△ABC 的形状.分析:如何将边角关系中的边化为角? → 再思考:又如何将角化为边?3. 小结:三角形解的情况的讨论;判断三角形类型;边角关系如何互化.三、巩固练习:1. 已知a 、b 为△ABC 的边,A 、B 分别是a 、b 的对角,且sin 2sin 3A B =,求a bb+的值2. 在△ABC 中,sin A :sin B :sin C =4:5:6,则cos A :cos B :cos C = .3. 作业:教材P11 B 组1、2题.教学设计(首页)学科:历史 教师:教学难点交通工具发展的对社会生活的影响教学用具文字、图片资料、多媒体课件教学方法讲述法、讨论法归纳法、小组讨论课时安排1板书设计教学反思2016 年 4 月30 日教学设计(续页)2016 年 4 月30日教学设计(续页)2016 年 4 月30日教学设计(续页)2016 年 4 月30日中国的铁路营运总里程已跃居亚洲第一位,世界第四位机车制造取得很大进展,1997年以来全国铁路实现了六次大提速教学设计(续页)2016 年 4 月30日教学设计(续页)2016 年 4 月30日教学设计(首页)学科:历史教师:教学用具文字、图片资料、多媒体课件教学方法讲述法、讨论法归纳法、小组讨论课时安排1板书设计教学反思2016 年 4 月30 日教学设计(续页)2016 年 4 月30日教学设计(续页)2016 年 4 月30日教学设计(续页)2016 年 4 月30日中国的铁路营运总里程已跃居亚洲第一位,世界第四位机车制造取得很大进展,1997年以来全国铁路实现了六次大提速教学设计(续页)2016 年 4 月30日教学设计(续页)2016 年 4 月30日。

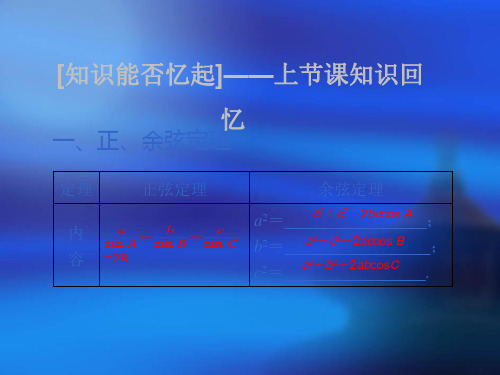
正弦定理和余弦定理讲义课前双击巩固1.正弦定理和余弦定理定理正弦定理余弦定理公式asinA= ==2R (其中R 是△ABC 的外接圆的半径)a 2= ,b 2= , c 2=定理的变形 a=2RsinA ,b= ,c=,a∶b∶c=cos A= , cos B= , cos C=2.在△ABC 中,已知a,b 和A 时,解的情况如下:A 为锐角A 为钝角或直角图形关系式a=bsin Absin A<a<b a ≥ba>b解的个数3.三角形面积公式(1)S=12ah (h 表示边a 上的高);(2)S=12bcsin A=12acsin B=12absin C ; (3)S=12r (a+b+c )(r 为三角形的内切圆半径). 常用结论1.三角形内角和定理:在△ABC 中,A+B+C=π;变形:A+B 2=π2-C 2.2.三角形中的三角函数关系:(1)sin(A+B)=sin C;(2)cos(A+B)=-cos C; (3)sinA+B 2=cos C 2;(4)cosA+B 2=sin C2.3.三角形中的射影定理在△ABC 中,a=bcos C+ccos B;b=acos C+ccos A;c=bcos A+acos B.题组一 常识题1.[教材改编] 在△ABC 中,B=45°,C=60°,c=2,则最短边的边长等于 .2.[教材改编] 在△ABC 中,已知a=5,b=2√3,C=30°,则c= .3.[教材改编] 在△ABC 中,已知a 2-c 2+b 2=ab ,则C 等于 .4.[教材改编] 在△ABC 中,已知a=3√2,b=2√3,cos C=13,则△ABC 的面积为 . 题组二 常错题◆索引:在△ABC 中角与角的正弦的关系;正弦定理求角时解的个数;余弦定理、面积公式中边与角的三角函数的对应关系.5.在△ABC 中,若sin A=sin B ,则A ,B 的关系为 ;若sin A>sin B ,则A ,B 的关系为 .6.在△ABC 中,若A=60°,a=4√3,b=4√2,则B 等于 .7.在△ABC 中,a=2,b=3,C=60°,则c= ,△ABC 的面积等于 .8.在△ABC 中,角A ,B ,C 满足sin Acos C-sin Bcos C=0,则三角形的形状为 .课堂考点探究探究点一 利用正弦﹑余弦定理解三角形1 △ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2c-a=2bcos A. (1)求角B 的大小;(2)若b=2√3,求a+c的最大值.[总结反思](1)正弦定理、余弦定理的作用是在已知三角形部分元素的情况下求解其余元素,基本思想是方程思想,即根据正弦定理、余弦定理列出关于未知元素的方程,通过解方程求得未知元素;(正弦定理、余弦定理的另一个作用是实现三角形边角关系的互化,解题时可以把已知条件化为角的三角函数关系,题时,常利用基本不等式或表示为三角形的某一内角的三角函数形式求解.式题(1)在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且满足(a-b)(sin A+sin B)=(c-b)sin C,若a=√3,则b2+c2的取值范围是( )A.(5,6]B.(3,5)C.(3,6]D.[5,6](2)如图3-22-1,在△ABC中,D是边AC上的点,且AB=AD,2AB=√3BD,BC=2BD,则sin C的值为.图3-22-1探究点二利用正弦﹑余弦定理判定三角形的形状2如图3-22-2所示,图3-22-2在△ABC中,D是BC的中点,已知∠BAD+∠C=90°,则△ABC的形状是.[总结反思]判断三角形形状实质上是在缺少部分条件的情况下解三角形,此时三角形的各个元素虽然不能具体确定,但可以确定其中某些元素的等量或者不等量关系,据此对三角形形状作出判断.式题在△ABC中,若sin A=2cos Bsin C,则△ABC的形状是.探究点三与三角形面积有关的问题3已知锐角三角形ABC的内角A,B,C的对边分别为a,b,c,且满足cos2B-cos2C-sin2A=-sin Asin B,sin(A-B)=cos(A+B).(1)求角A,B,C;(2)若a=√2,求三角形ABC的边长b的值及三角形ABC的面积.[总结反思](1)若已知一个角(角的大小或该角的正弦值、余弦值),一般结合题意求夹这个角的两边或两边之积,再代入公式求解;(2)若已知三边,可先求一个角的余弦值,再求正弦值,代入,一般表示为一个内角的三角函数,,或结合基本不等式求解.式题△ABC的内角A,B,C的对边分别为a,b,c,已知a(sin A-sin B)=(c-b)(sin C+sin B).(1)求角C;(2)若c=√7,△ABC的面积为3√3,求△ABC的周长.2课时作业一、 填空题1.设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若a =2,c =23,cos A =32且b <c ,则b 等于________.2.已知△ABC ,a =5,b =15,A =30°,则c =________.3.已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c,23cos 2A +cos 2A =0,a =7,c =6,则b 等于________.4.设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若bcosC +ccosB =asinA ,则△ABC 的形状为________.5.在某次测量中,在A 处测得同一平面方向的B 点的仰角是50°,且到A 的距离为2,C 点的俯角为70°,且到A 的距离为3,则B 、C 间的距离为________.6.△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .若B =2A ,a =1,b =3,则c =________. 7.在△ABC 中,∠ABC =π4,AB =2,BC =3,则sin ∠BAC =________.8.在△ABC 中,内角A ,B ,C 所对应的边分别是a ,b ,c .若c 2=(a -b )2+6,C =π3,则△ABC 的面积是________.9.在△ABC 中,AC =3,A =45°,C =75°,则BC =________.10.设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且a =2,cos C =-14,3sin A =2sin B ,则c=________.11.在△ABC 中,a =3,b =6,A =2π3,则B =________.二、解答题12.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知△ABC 的面积为315,b -c =2,cos A =-14.(1)求a 和sin C 的值;(2)求cos ⎝⎛⎭⎫2A +π6的值.13.已知a ,b ,c 分别为△ABC 内角A ,B ,C 的对边,sin 2B =2sin A sin C . (1)若a =b ,求cos B ;(2)设B =90°,且a =2,求△ABC 的面积.。
铭智教育一对一个性化教案学生姓名教师姓名授课日期授课时段课题正弦定理和余弦定理重难点1.正弦定理和余弦定理2.正弦定理和余弦定理的灵活应用教学步骤及教学内1.正弦定理:asin A=bsin B=csin C=2R,其中R是三角形外接圆的半径.由正弦定理可以变形:(1)a∶b∶c =sin_A∶sin_B∶sin_C;(2)a=2R sin_A,b=2R sin_B,c=2R sin_C;(3)sin A=a2R,sin B=b2R,sin C =c2R等形式,以解决不同的三角形问题.2.余弦定理:a2=b2+c2-2bc cos_A,b2=a2+c2-2ac cos_B,c2=a2+b2-2ab cos_C.余弦定理可以变形:cos A=b2+c2-a22bc,cos B=a2+c2-b22ac,cos C=a2+b2-c22ab.3.S△ABC=12ab sin C=12bc sin A=12ac sin B=abc4R=12(a+b+c)·r(r是三角形内切圆的半径),并可由此计算R、r.4.在△ABC中,已知a、b和A时,解的情况如下:A为锐角A为钝角或直角教育要对民族的未来负责教育要对民族的未来负责容图形关系式 a =b sin A b sin A <a <b a ≥b a >b 解的个数一解两解一解一解[难点正本 疑点清源]1.在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ABC 中,A >B ⇔a >b ⇔sin A >sin B .2. 根据所给条件确定三角形的形状,主要有两种途径:(1)化边为角;(2)化角为边,并常用正弦(余弦)定理实施边、角转换.1. 在△ABC 中,若A =60°,a =3,则a +b +csin A +sin B +sin C=________.答案 2解析 由正弦定理及等比性质知a sin A =b sin B =csin C =a +b +c sin A +sin B +sin C =2R , 而由A =60°,a =3,得a +b +c sin A +sin B +sin C=2R =a sin A =3sin 60°=2.2. (2012·福建)已知△ABC 的三边长成公比为2的等比数列,则其最大角的余弦值为________.答案 -24解析 设三角形的三边长从小到大依次为a ,b ,c , 由题意得b =2a ,c =2a . 在△ABC 中,由余弦定理得cos C =a 2+b 2-c 22ab =a 2+2a 2-4a 22×a ×2a=-24.教育要对民族的未来负责3. (2012·重庆)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且cos A =35,cos B =513,b =3,则c=________. 答案145解析 在△ABC 中,∵cos A =35>0,∴sin A =45.∵cos B =513>0,∴sin B =1213.∴sin C =sin [π-(A +B )]=sin(A +B ) =sin A cos B +cos A sin B =45×513+35×1213=5665. 由正弦定理知b sin B =csin C ,∴c =b sin Csin B =3×56651213=145.4. (2011·课标全国)在△ABC 中,B =60°,AC =3,则AB +2BC 的最大值为________.答案 27解析 由正弦定理知AB sin C =3sin 60°=BCsin A, ∴AB =2sin C ,BC =2sin A .又A +C =120°,∴AB +2BC =2sin C +4sin(120°-C ) =2(sin C +2sin 120°cos C -2cos 120°sin C ) =2(sin C +3cos C +sin C )=2(2sin C +3cos C )=27sin(C +α), 其中tan α=32,α是第一象限角, 由于0°<C <120°,且α是第一象限角, 因此AB +2BC 有最大值27.教育要对民族的未来负责5. 已知圆的半径为4,a 、b 、c 为该圆的内接三角形的三边,若abc =162,则三角形的面积为( )A .2 2B .8 2 C. 2D.22答案 C解析 ∵a sin A =b sin B =c sin C =2R =8,∴sin C =c8,∴S △ABC =12ab sin C =116abc =116×162= 2.题型一 利用正弦定理解三角形例1 在△ABC 中,a =3,b =2,B =45°.求角A 、C 和边c .思维启迪:已知两边及一边对角或已知两角及一边,可利用正弦定理解这个三角形,但要注意解的个数的判断.解 由正弦定理得a sin A =b sin B ,3sin A =2sin 45°,∴sin A =32. ∵a >b ,∴A =60°或A =120°.当A =60°时,C =180°-45°-60°=75°,c =b sin C sin B =6+22;当A =120°时,C =180°-45°-120°=15°, c =b sin Csin B =6-22.探究提高 (1)已知两角及一边可求第三角,解这样的三角形只需直接用正弦定理代入求解即可. (2)已知两边和一边对角,解三角形时,利用正弦定理求另一边的对角时要注意讨论该角,这是解题的难点,应引起注意.已知a ,b ,c 分别是△ABC 的三个内角A ,B ,C 所对的边,若a =1,b =3,A +C =2B ,则角A 的大小为________. 答案 π6教育要对民族的未来负责解析 ∵A +C =2B 且A +B +C =π,∴B =π3.由正弦定理知:sin A =a sin B b =12,又a <b ,∴A <B ,∴A =π6.题型二 利用余弦定理求解三角形例2 在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,且cos B cos C =-b2a +c.(1)求角B 的大小;(2)若b =13,a +c =4,求△ABC 的面积.思维启迪:由cos B cos C =-b2a +c ,利用余弦定理转化为边的关系求解.解 (1)由余弦定理知:cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab .将上式代入cos B cos C =-b2a +c 得:a 2+c 2-b 22ac ·2ab a 2+b 2-c 2=-b 2a +c , 整理得:a 2+c 2-b 2=-ac . ∴cos B =a 2+c 2-b 22ac =-ac 2ac =-12.∵0<B <π,∴B =23π.(2)将b =13,a +c =4,B =23π代入b 2=a 2+c 2-2ac cos B ,得b 2=(a +c )2-2ac -2ac cos B , ∴13=16-2ac ⎝⎛⎭⎫1-12,∴ac =3. ∴S △ABC =12ac sin B =334.教育要对民族的未来负责探究提高 (1)根据所给等式的结构特点利用余弦定理将角化边进行变形是迅速解答本题的关键. (2)熟练运用余弦定理及其推论,同时还要注意整体思想、方程思想在解题过程中的运用.已知A ,B ,C 为△ABC 的三个内角,其所对的边分别为a ,b ,c ,且2cos 2A2+cos A =0.(1)求角A 的值;(2)若a =23,b +c =4,求△ABC 的面积. 解 (1)由2cos 2A2+cos A =0,得1+cos A +cos A =0,即cos A =-12,∵0<A <π,∴A =2π3.(2)由余弦定理得,a 2=b 2+c 2-2bc cos A ,A =2π3,则a 2=(b +c )2-bc ,又a =23,b +c =4,有12=42-bc ,则bc =4, 故S △ABC =12bc sin A = 3.题型三 正弦定理、余弦定理的综合应用例3 (2012·课标全国)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,a cos C +3a sin C -b -c =0. (1)求A ;(2)若a =2,△ABC 的面积为3,求b ,c .思维启迪:利用正弦定理将边转化为角,再利用和差公式可求出A ;面积公式和余弦定理相结合,可求出b ,c .解 (1)由a cos C +3a sin C -b -c =0及正弦定理得sin A cos C +3sin A sin C -sin B -sin C =0. 因为B =π-A -C ,所以3sin A sin C -cos A sin C -sin C =0. 由于sin C ≠0,所以sin ⎝⎛⎭⎫A -π6=12.教育要对民族的未来负责又0<A <π,故A =π3.(2)△ABC 的面积S =12bc sin A =3,故bc =4.而a 2=b 2+c 2-2bc cos A ,故b 2+c 2=8. 解得b =c =2.探究提高 在已知关系式中,若既含有边又含有角.通常的思路是将角都化成边或将边都化成角,再结合正、余弦定理即可求角.在△ABC 中,内角A ,B ,C 所对的边长分别是a ,b ,c .(1)若c =2,C =π3,且△ABC 的面积为3,求a ,b 的值;(2)若sin C +sin(B -A )=sin 2A ,试判断△ABC 的形状. 解 (1)∵c =2,C =π3,∴由余弦定理c 2=a 2+b 2-2ab cos C 得a 2+b 2-ab =4. 又∵△ABC 的面积为3,∴12ab sin C =3,ab =4.联立方程组⎩⎪⎨⎪⎧a 2+b 2-ab =4,ab =4,解得a =2,b =2.(2)由sin C +sin(B -A )=sin 2A , 得sin(A +B )+sin(B -A )=2sin A cos A ,即2sin B cos A =2sin A cos A ,∴cos A ·(sin A -sin B )=0, ∴cos A =0或sin A -sin B =0, 当cos A =0时,∵0<A <π, ∴A =π2,△ABC 为直角三角形;当sin A -sin B =0时,得sin B =sin A , 由正弦定理得a =b ,教育要对民族的未来负责即△ABC 为等腰三角形.∴△ABC 为等腰三角形或直角三角形.代数化简或三角运算不当致误典例:(12分)在△ABC 中,若(a 2+b 2)sin(A -B )=(a 2-b 2)·sin(A +B ),试判断△ABC 的形状.审题视角 (1)先对等式化简,整理成以单角的形式表示.(2)判断三角形的形状可以根据边的关系判断,也可以根据角的关系判断,所以可以从以 下两种不同方式切入:一、根据余弦定理,进行角化边;二、根据正弦定理,进行边化 角.规范解答解 ∵(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ),∴b 2[sin(A +B )+sin(A -B )]=a 2[sin(A +B )-sin(A -B )], ∴2sin A cos B ·b 2=2cos A sin B ·a 2, 即a 2cos A sin B =b 2sin A cos B .[4分]方法一 由正弦定理知a =2R sin A ,b =2R sin B , ∴sin 2A cos A sin B =sin 2B sin A cos B , 又sin A sin B ≠0,∴sin A cos A =sin B cos B , ∴sin 2A =sin 2B .[8分]在△ABC 中,0<2A <2π,0<2B <2π,∴2A =2B 或2A =π-2B ,∴A =B 或A +B =π2.∴△ABC 为等腰或直角三角形.[12分] 方法二 由正弦定理、余弦定理得: a 2bb 2+c 2-a 22bc =b 2a a 2+c 2-b 22ac,[6分] ∴a 2(b 2+c 2-a 2)=b 2(a 2+c 2-b 2),教育要对民族的未来负责∴(a 2-b 2)(a 2+b 2-c 2)=0, ∴a 2-b 2=0或a 2+b 2-c 2=0.[10分] 即a =b 或a 2+b 2=c 2.∴△ABC 为等腰或直角三角形.[12分]温馨提醒 (1)利用正弦、余弦定理判断三角形形状时,对所给的边角关系式一般都要先化为纯粹的边之间的关系或纯粹的角之间的关系,再判断.(2)本题也可分析式子的结构特征,从式子看具有明显的对称性,可判断图形为等腰或直角三角形. (3)易错分析:①方法一中由sin 2A =sin 2B 直接得到A =B ,其实学生忽略了2A 与2B 互补的情况,由于计算问题出错而结论错误.方法二中由c 2(a 2-b 2)=(a 2+b 2)(a 2-b 2)不少同学直接得到c 2=a 2+b 2,其实是学生忽略了a 2-b 2=0的情况,由于化简不当致误.②结论表述不规范.正确结论是△ABC 为等腰三角形或直角三角形,而不少学生回答为:等腰直角三角形.高考中的解三角形问题典例:(12分)(2012·辽宁)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .角A ,B ,C 成等差数列.(1)求cos B 的值;(2)边a ,b ,c 成等比数列,求sin A sin C 的值.考点分析 本题考查三角形的性质和正弦定理、余弦定理,考查转化能力和运算求解能力. 解题策略 根据三角形内角和定理可直接求得B ;利用正弦定理或余弦定理转化到只含角或只含边的式子,然后求解. 规范解答解 (1)由已知2B =A +C ,A +B +C =180°,解得B =60°, 所以cos B =12.[4分](2)方法一 由已知b 2=ac ,及cos B =12,根据正弦定理得sin 2B =sin A sin C ,[8分] 所以sin A sin C =1-cos 2B =34.[12分]教育要对民族的未来负责方法二 由已知b 2=ac ,及cos B =12,根据余弦定理得cos B =a 2+c 2-b 22ac =a 2+c 2-ac 2ac =12,解得a =c ,[8分]所以A =C =B =60°,故sin A sin C =34.[12分]解后反思 (1)在解三角形的有关问题中,对所给的边角关系式一般要先化为只含边之间的关系或只含角之间的关系,再进行判断.(2)在求解时要根据式子的结构特征判断使用哪个定理以及变形的方向.方法与技巧1.应熟练掌握和运用内角和定理:A +B +C =π,A 2+B 2+C 2=π2中互补和互余的情况,结合诱导公式可以减少角的种数.2.正、余弦定理的公式应注意灵活运用,如由正、余弦定理结合得sin 2A =sin 2B +sin 2C - 2sin B ·sin C ·cos A ,可以进行化简或证明. 失误与防范1.在利用正弦定理解已知三角形的两边和其中一边的对角求另一边的对角,进而求出其他的边和角时,有时可能出现一解、两解,所以要进行分类讨论.2.利用正、余弦定理解三角形时,要注意三角形内角和定理对角的范围的限制.A 组 专项基础训练 (时间:35分钟,满分:57分)一、选择题(每小题5分,共20分)1. (2012·广东)在△ABC 中,若∠A =60°,∠B =45°,BC =32,则AC 等于( )A .4 3B .2 3 C. 3 D.32答案 B教育要对民族的未来负责解析 在△ABC 中,AC sin B =BCsin A, ∴AC =BC ·sin Bsin A =32×2232=2 3.2. (2011·浙江)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若a cos A =b sin B ,则sin A cos A +cos 2B 等于( )A .-12B.12C .-1D .1答案 D解析 ∵a cos A =b sin B ,∴sin A cos A =sin B sin B , 即sin A cos A -sin 2B =0,∴sin A cos A -(1-cos 2B )=0, ∴sin A cos A +cos 2B =1.3. 在△ABC 中,a ,b ,c 分别为角A ,B ,C 所对的边,若a =2b cos C ,则此三角形一定是( )A .等腰直角三角形B .直角三角形C .等腰三角形D .等腰三角形或直角三角形答案 C解析 因为a =2b cos C ,所以由余弦定理得a =2b ·a 2+b 2-c 22ab ,整理得b 2=c 2,因此三角形一定是等腰三角形.4. (2012·湖南)△ABC 中,AC =7,BC =2,B =60°,则BC 边上的高等于( )A.32B.332C.3+62D.3+394答案 B解析 设AB =a ,则由AC 2=AB 2+BC 2-2AB ·BC cos B 知7=a 2+4-2a ,即a 2-2a -3=0,∴a =3(负值舍去).∴BC 边上的高为AB ·sin B =3×32=332. 二、填空题(每小题5分,共15分)教育要对民族的未来负责5. (2011·北京)在△ABC 中,若b =5,∠B =π4,sin A =13,则a =________.答案523解析 根据正弦定理应有a sin A =b sin B, ∴a =b sin Asin B =5×1322=523.6. (2011·福建)若△ABC 的面积为3,BC =2,C =60°,则边AB 的长度等于________.答案 2解析 由于S △ABC =3,BC =2,C =60°, ∴3=12×2·AC ·32,∴AC =2,∴△ABC 为正三角形.∴AB =2.7. 在△ABC 中,若AB =5,AC =5,且cos C =910,则BC =________.答案 4或5解析 设BC =x ,则由余弦定理AB 2=AC 2+BC 2-2AC ·BC cos C 得5=25+x 2-2·5·x ·910,即x 2-9x+20=0,解得x =4或x =5. 三、解答题(共22分)8. (10分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足cos A 2=255,AB →·AC →=3.(1)求△ABC 的面积; (2)若b +c =6,求a 的值.解 (1)∵cos A 2=255,∴cos A =2cos 2A 2-1=35,∴sin A =45.又AB →·AC →=3,∴bc cos A =3,∴bc =5.∴S △ABC =12bc sin A =12×5×45=2.(2)由(1)知,bc =5,又b +c =6,教务处签字:日期:年月日课后评价一、学生对于本次课的评价○特别满意○满意○一般○差二、教师评定1、学生上次作业评价:○好○较好○一般○差2、学生本次上课情况评价:○好○较好○一般○差作业布置.s.5.u.根据余弦定理得a2=b2+c2-2bc cos A=(b+c)2-2bc-2bc cos A=36-10-10×35=20,∴a=2 5.教育要对民族的未来负责教师留言教师签字:家长意见家长签字:日期:年月日教育要对民族的未来负责。