下载文档原格式
圆外一点做圆切线的作图法(仅直尺)利用直尺和圆规过已知圆外一点作这个圆的切线，是一个比较简单的作图问题．但是，如果只利用直尺来完成这个作图问题，想必是中学时候未曾想过的问题事实上这是可以的,下面我们就来说明这样的一个事情:作法：1．作圆的三条割线PEC、PFD、PGH，交点如图示．2．连结DE、CF交于X，连结DG、HF交于Y．3．作直线XY交圆于A、B．4．作直线PA、PB，则PA、PB就是所求作的圆的切线．那么我们接下来就对其进行证明:首先引入两个引理：先给出一个定理引理1：在圆内接六边形ABCDEF中，若AB·CD·EF=FA·BC·DE，则AD、BE、CF相交于一点．证明设AD、BE相交于G，连结FG，并延长FG交⊙O于C＇，再连结BC＇、C＇D．易知△AGB∽△EGD，△C＇GD∽△AGF，△EGF∽△C＇GB.所以有',,'AB BG C D DG EF FG DE DG AF FG BC BG === 由之可得'1'AB C D EF DE AF BC ⋅⋅=，即''AB C D EF FA BC DE ⋅⋅=⋅⋅与已知式子相比较得''C D BC CD BC =即''CD BC BC C D ⋅=⋅ (1)连结CC ’、BD ，在园内接四边形BCC ’D 中，由托勒密定理，得'''CD BC BC C D BD CC ⋅=⋅+⋅ (2)(1)(2),那么可知 '0BD CC ⋅= 即 '0CC =从而可知C 、C ’两点重合，于是AD 、BE 、CF 相交于一点． # 注：托勒密定理：圆内接四边形中，两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和)．已知：圆内接四边形ABCD ，求证：AC·BD＝AB·CD ＋AD·BC．证明：如上图，过C 作CP 交BD 于P ，使∠1=∠2，又∠3=∠4，∴△ACD∽△BCP．得AC ：BC=AD ：BP ，AC·BP=AD·BC ①。
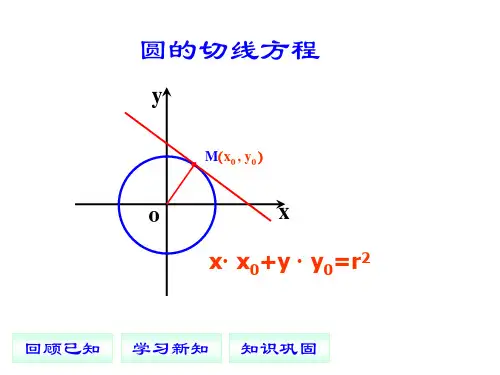
关于圆的切线方程的推导已知⊙O 的方程为()()222r b y a x =-+-以及一点()00,y x P ，求过点P 的⊙O 的切线方程.①当点P 在⊙O 上时，连接OP ，如图所示设直线OP 的方程为111m x k y +=，由()b a O ,和()00,y x P 得a xb y k y m k x b m ak --=⇒⎩⎨⎧=+=+001011011，从而有过点P 的圆的切线方程的斜率为by a x k ---='001 因为点P 在圆上，所以有()0000x x b y a x y y ----=-，展开得000002020=----+++yy xx by ax by ax y x将上式整理得 ()()()()20000r b y y y a x x x =--+--②当点P 在⊙O 外时，存在两条关于⊙O 的切线方程，如图所示设⊙O 的切线方程为222m x k y +=，由于切线过点()00,y x P 得00222y x k x k y +-=，化为一般式000222=+--y x k y x k由方程()()222r b y a x =-+-得点O 的坐标为()b a ,因为直线与圆相切，所以点O 到切线的距离等于圆的半径r 故有()()2002222222002211y x k b ak k r r k y x k b ak +--=+⇒=++-- 022222222220202002020220222022222=---++-++--+r r k by y b y x k x bk y ak abk x ak x k k a()()()022220202000022020222=--+++-----+r by y b y x bx ay ab k r ax x a k ()[]()()[]022200000222022=--++-----r y b y x bx ay ab k r x a k ()()()()2202202000002r x a r b y a x r y x bx ay ab k ----+-±+--=由上述方程00222y x k x k y +-=得 ()()()()()()()()22002000002202202000002r x a b y a x r y x bx ay ab x r x a r b y a x r y x bx ay ab y ---+-±+-------+-±+--=文 - 汉语汉字 编辑词条 文，wen ，从玄从爻。
过点作圆的切线1. 引言在几何学中，切线是一条与曲线相切的直线。
本文将讨论如何求解过给定点作圆的切线方程。
这个问题在数学和物理学中都有广泛的应用，尤其是在曲线的研究和问题求解中。
2. 基本概念在讨论过点作圆的切线之前，我们先来了解一些基本概念。
2.1 圆圆是一个平面上所有到一个固定点距离相等的点所组成的集合。
这个固定点被称为圆心，而所有到圆心距离相等的距离被称为半径。
2.2 切线切线是一条与曲线相切且只与曲线有一个公共交点的直线。
在几何学中，我们经常使用切线来研究曲线的性质和求解相关问题。
3. 求解过点作圆的切线方程3.1 圆心和半径已知情况下假设我们已知一个圆心坐标为(a,b)，半径为r，以及一个外部点P(x0,y0)。
我们需要求解过点P作圆的切线方程。
首先，我们需要确定点P与圆的位置关系。
根据勾股定理，点P到圆心的距离为：d=√(x0−a)2+(y0−b)2如果d<r，则点P在圆内；如果d=r，则点P在圆上；如果d>r，则点P在圆外。
对于切线方程的求解，我们只需要考虑d<r的情况。
在这种情况下，我们可以得到两条切线。
设切线与x轴的夹角为θ1和θ2由图可知，tan(θ1)=tan(θ2)=y0−bx0−a因此，θ1=arctan(y0−bx0−a)θ2=arctan(y0−bx0−a)+π其中arctan()是反正切函数。
根据直线与x轴夹角和斜率之间的关系，我们可以得到切线的斜率：k1=tan(θ1)k2=tan(θ2)因此，切线方程可以表示为：y−y0=k1(x−x0)y−y0=k2(x−x0)将切线方程整理为一般形式：y=k1x+(y0−k1x0)y=k2x+(y0−k2x0)这样，我们就得到了过点P作圆的两条切线方程。
3.2 圆上一点已知情况下现在假设我们已知一个圆心坐标为(a,b)，半径为r，以及一个圆上的点Q(x q,y q)。
我们需要求解过点Q作圆的切线方程。
与前面类似，首先我们需要确定点Q与圆的位置关系。
过圆外一点求圆的切线方程在数学中，求解过圆外一点的切线方程是一个经典问题。
我们首先需要明确一些基本概念。
圆是由一组等距离于圆心的点组成的集合。
一个圆由其圆心和半径确定。
圆心是圆的中心点，而半径是从圆心到圆上任意一点的距离。
切线是与圆相切的直线。
它只与圆相交于切点，并且在切点处与圆相切。
切线与圆的切点处的切线向量与圆的半径向量垂直。
现在，我们来考虑如何求解过圆外一点的切线方程。
假设我们有一个圆，已知其圆心坐标为（a，b），半径为r。
我们还有一个点P，其坐标为（x，y），且点P在圆的外部。
我们需要找到点P到圆心的距离。
根据勾股定理，点P到圆心的距离可以表示为：√((x - a)^2 + (y - b)^2)接下来，我们需要找到过点P的切线的斜率。
切线的斜率可以通过计算点P到圆心的连线与切线的夹角来得到。
根据几何性质，点P 到圆心的连线与切线的夹角等于切线与圆的半径的夹角。
因此，我们可以使用以下公式来计算切线的斜率：斜率 = -((x - a) / (y - b))接下来，我们需要找到切线的截距。
我们可以使用点斜式来表示切线的方程，其中切线的斜率为m，切点的坐标为（x0，y0）。
切线的方程可以表示为：y - y0 = m(x - x0)我们已经找到了切线的斜率和一个切点，即点P。
我们可以将切线的方程表示为：y - y1 = m(x - x1)其中，m是切线的斜率，（x1，y1）是点P的坐标。
现在，我们已经成功地求解了过圆外一点的切线方程。
通过这个方程，我们可以得到切线的斜率和截距，从而可以确定切线的方程。
经过圆一点的切线方程
本篇文章将介绍如何求解经过圆上一点的切线方程。
首先，我们需要了解圆的基本概念和性质。
圆是一个由一条固定的曲线组成的几何图形，其中每个点到圆心的距离都相等。
圆的切线是一个经过圆上一点的直线，与圆的切点处切线与圆的切线垂直。
要求解经过圆上一点的切线方程，我们需要使用以下公式：
1. 圆的标准方程：$(x-a)^2 + (y-b)^2 = r^2$
其中，$(a,b)$是圆心的坐标，$r$是圆的半径。
2. 切线的斜率公式：$y = mx + n$
其中，$m$是切线的斜率，$n$是切线的截距。
3. 切线与圆的切点处切线垂直：$m = -frac{1}{k}$
其中，$k$是圆的切点处的切线斜率。
基于以上公式，我们可以按照以下步骤求解经过圆上一点的切线方程：
步骤1：找到圆心的坐标和圆的半径。
步骤2：找到经过圆上一点的直线的斜率。
步骤3：计算圆上切点处切线的斜率。
步骤4：结合切线的斜率公式和切线与圆的切点处切线垂直的条件，求解切线的截距。
步骤5：用切线的斜率和截距，得到切线的方程。
通过以上步骤，我们可以求解经过圆上一点的切线方程，进而更好地理解圆的性质和特点。
