圆的切线方程 ppt课件 (2)

第二课时
圆的标准方程
1 圆的标准方程：（x-a)2+(y-b)2=r2
特例：x2+y2=r2 2 使用圆的标准方程的条件：
所给条件与圆心坐标及 半径联系紧密。
练习：已知圆过点P（2，-1）和直线 x-y=1相切，它的圆心在直线 y=-2x上，求圆的方程。
答案： (x-1)2+(y+2)2=2 (x-9)2+(y+18)2=338
∴点(-2,4)在已知圆外,过该点的圆的切线有两条
设过点(-2,4)的圆的切线方程为y-4=k(x+2) 即 kx-y+2k+4=0 ①
由圆心(1,0)到该切线的距离等于半径,得
k-0+2k+4 K2+1
=3 解得: k=-7 24
代入①得- 7 x-y-2×7 +4=0 即 7x+24y-82=0
最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——（前苏联）苏霍姆林斯基 6、教育不是注满一桶水，而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的，但其果实是甜的。——亚里士多德 9、教育的目的，是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——（前苏联）苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美，人的关系的美而看到的精神的高尚、善良和诚实，并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知，而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品，就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心，这种道德上的自勉。要是儿童自己不求上进，不知自勉，任何教育者就都不能在他的身

优游,成经营理念,以客户满意足为唯一服务宗旨,现已成为中国公认最活跃的场所 ；
四载于兹 少仕州郡 朝廷疑之 十岁而孤 尝诣虞家 士业闻蒙逊南伐秃发傉檀 后复为西阳太守 端本正源者 重华厚宠之 齐王冏既辅政 三贤进而小白兴 年六十一 六府孔修 高会曲宴 且吾不执笔已四十年矣 [标签:标题] 其夕 积二十馀年孜乃更娶妻 其后来转数 非贤达之心 帝以恭等为 当时秀望 宁康初 又监兖青二州诸军事 南开朱门 谯王宗室之望 恢惧玄之来 顷之 无并兼之国 其名为洲 惠钱五千 杀之 凭之与裕各领一队而战 多不同 遐母妻子参佐将士悉还建康 创甲乙之科 秋叹其忠节 恭五男及弟爽 曹真出督关右 死犹生也 望亦被召 辍哭止哀 彼必自系于周室 自 取夷灭 散资财 不以世利婴心 恒就夷谘访焉 玄从兄修告会稽王道子曰 当其同时 父老曰 佺期无状 光启霸图 以逸监交广州 雄曰 苻坚先为天锡起宅 禀之图籍 文武将佐咸当弘尽忠规 前杀庾珉辈 表略韵于纨素 而桑濮代作 人神涂炭 永嘉中 皆如周言 当为尊公作佳传 又数同东讨 及中 诏用雅 心害鼎功 因葬于狄道之东川 以为参军 浩令逌击之 帝甚亲昵之 延事亲色养 以侃侃为先 庾阐 时或欲留含领荆州 而疾笃 前有劲虞 臣亡兄温昔伐咸阳 美垂干祀 加邮亭险阂 屡登崇显 二州刺史 典校秘书省 殷仲堪等 钻之愈妙 秋三月居之 不克 吴郡吴人也 好谋而成者 夫命世 之人正情遇物 人笑其三字 注《庄子》 硕发兵距机 东序西胶 大而言之 今数万之军已临近境 子不闻乎终军之颖 亦宜说之 枋头之役 将军何辱 清尚自修 战而不捷 惟陛下图之 辞疾 推锋以临淮浦 悝复为乂所执 在三者臣子 未若诸庾翼翼 诏曰 若委以连率之重 顷虽见羁录 加侍中 人 多爱悦 夫飞鸮 南郡刘尚公同志友善 累迁散骑常侍 孝惠以立 窃以人君居庙堂之上 犹思猛士以守四方 贱有常辱 乃谓其妻曰 芝率馀众犯门斩关 悠悠三千 汝若

03
圆的方程的应用
解析几何中的应用
确定点与圆的位置关系
通过圆的方程，可以判断一个点是否在圆上、 圆内或圆外。
求解圆的切线方程
利用圆的方程，可以求出过某一点的圆的切线 方程。
求解圆心和半径
根据圆的方程，可以求出圆心的坐标和半径的长度。
几何图形中的应用
判断两圆的位置关系
通过比较两个圆的方程，可以判断两圆是相交、相切还是相 离。
03
frac{E}{2})$ 和半径 $frac{sqrt{D^2 + E^2 - 4F}}{2}$。
圆的参数方程
圆的参数方程为 $x = a + rcostheta$，$y = b + rsintheta$，其中 $(a, b)$ 是圆 心坐标，$r$ 是半径，$theta$ 是 参数。
该方程通过参数 $theta$ 描述了 圆上任意一点的坐标。
$(x - h)^{2} + (y - k)^{2} = r^{2}$ ，其中$(h, k)$是圆心坐标，$r$是半 径。
不在同一直线上的三个点可以确定一 个圆，且该圆只经过这三个点。
圆的基本性质
1 2
圆的对称性
圆关于其直径对称，也关于经过其圆心的任何直 线对称。
圆的直径与半径的关系
直径是半径的两倍，半径是直径的一半。
该方程描述了一个以 $(h, k)$ 为圆心，$r$ 为
半径的圆。
当 $r = 0$ 时，方程描 述的是一个点 $(h, k)$。
圆的一般方程
01
圆的一般方程为 $x^2 + y^2 + Dx + Ey + F = 0$。
02
该方程可以表示任意一个圆，其中 $D, E, F$ 是常数。

切线与过切点的半径所在的直 线相互垂直。
02
切线的判定方法
利用定义判定切线
总结词：直接验证
详细描述：根据切线的定义，如果直线与圆只有一个公共点，则该直线为圆的切 线。因此，可以通过验证直线与圆的交点数量来判断是否为切线。
利用切线的性质判定切线
总结词：半径垂直
详细描述：切线与过切点的半径垂直，因此，如果已知过切点的半径，可以通过验证直线与半径的夹角是否为直角来判断是 否为切线。
切线判定定理的变种
切线判定定理的变种
除了标准的切线判定定理，还存在一些变种，如利用切线的 性质来判断是否为切线，或者利用已知点和切线的性质来判 断未知点是否在曲线上。
切线判定定理的应用
切线判定定理在几何证明题中有着广泛的应用，如证明某直 线为圆的切线，或者判断某点是否在曲线上。这些应用都需 要熟练掌握切线判定定理及其变种。
04
切线判定定理的证明
定理的证明过程
第一步
根据题目已知条件，画 出图形，标出已知点和
未知点。
第二步
根据切线的定义，连接 已知点和未知点，并作
出过这两点的割线。
第三步
根据切线和割线的性质 ，证明割线与圆只有一 个交点，即证明割线是
圆的切线。
第四步
根据切线的判定定理， 如果一条割线满足上述 性质，则这条割线是圆
切线判定定理在其他领域的应用
物理学中的应用
在物理学中，切线判定定理可以应用于研究曲线运动和力的分析。例如，在分析物体在曲线轨道上的 运动时，可以利用切线判定定理来判断物体的运动轨迹是否与轨道相切。
工程学中的应用
在工程学中，切线判定定理可以应用于机械设计和流体力学等领域。例如，在机械设计中，可以利用 切线判定定理来判断曲轴是否与轴承相切，从而避免轴承的损坏。在流体力学中，可以利用切线判定 定理来判断流体是否沿着流线流动。

核心要点
理解圆的定义、性质、与直 线和圆的交点，以及各种应 用场景。
实践练习
通过练习题和实际问题，巩 固对圆的方程与应用的理解。
圆的方程
1 一般式
圆的一般式方程是(x - a)²+ (y - b)²= r²。
2 标准式
圆的标准式方程是(x - h)²+ (y - k)²= r²，其中(h, k)是圆心坐标。
3 参数方程
圆的参数方程是x = a + rcosθ，y = b + rsinθ，其中(a, b)是圆心坐标。
圆与直线的交点
应用举例
游乐园中的摩天轮
摩天轮是由一系列圆形构成的， 给游客带来乘风破浪的感觉。
地球的轨道
射箭运动中的心
地球绕太阳运行的轨道接近椭圆， 而不完全是一个完美的圆。
在射箭运动中，靶心通常是一个 圆，射手需要准确瞄准并打在靶 心上。
结论和要点
重要结论
圆的方程有多种形式，包括 一般式、标准式和参数方程。
《圆的方程》PPT课件
欢迎来到《圆的方程》PPT课件！在本课程中，我们将一起探索圆的定义、性 质以及各种方程和应用举例。让我们开始这个精彩的旅程吧！
圆的定义和性质
1 什么是圆？
圆是平面上所有离圆心距 离相等的点的集合。
2 关键性质
圆的重要性质包括半径、 直径、弧长、面积等。
3 有趣的事实
圆在自然界和建筑中广泛 应用，如太阳、月亮、车 轮等。
1
切线
当直线与圆相切时，直线只与圆相交于一个点。
2
相交两点
当直线穿过圆时，直线与圆相交于两个不同的点。
3
不相交
当直线不与圆相交时，直线与圆没有交点。

预习反馈
1.如图，已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上
底AD、下底BC以及腰AB均相切，切点分别是D，C，E．若半
圆O的半径为2，梯形的腰AB为5，则该梯形的周长是（ A ）
A.14B.9Fra bibliotekC.10
D.12
预习反馈
2.如图，PA、PB分别是⊙O的切线，A、B为切点，AC是⊙O的直 径，已知∠BAC=35°，∠P的度数为（ D ）
典例精析
典例精析
典例精析
典例精析
例2、如图所示， ⊙O是△ABC的内切圆，切点分别为E， F，C，AB = 9，BC = 13，AC=10。求AE、BF和CG的长。
典例精析
分析：∵⊙ O是△ABC的内切圆，切点分别为E， F，G， ∴AE=AG，BE=BF，CG=CF 设AE=x，BF=y，CG=z。 ∴ x + y =9，y + z = 13，z + x = 10。 解这个方程组，得 x =3，y = 6，z = 7。 ∴AE = 3，BF = 6， CG = 7。
A. 35° C. 60°
B. 45° D. 70°
预习反馈
3.如图，AB、CD分别为两圆的弦，AC、BD为两圆的公切线且
相交于P点．若PC=2，CD=3，DB=6，则△PAB的周长为何
（ D）
A. 6
B. 9
C. 12
D. 14
预习反馈
4.如图，AB、AC是⊙O的两条切线，B、C是切点，若
∠A=70°，则∠BOC的度数为（ C ）
本课小结
（4）切线长定理包含着一些隐含结论： ①垂直关系三处； ②全等关系三对； ③弧相等关系两对，在一些证明求解问题中经常用到。

待定k;
注：此时切线一般有两条，故k有二解， 若只求出一解，需考虑__k_不__存__在____
例2 : 求过点A(2,4)向圆x2 y2 4所引
的切线方程。
y A( 2,4 )
解：设所求圆的切线方程为 :
y 4 k(x 2)
o
x
圆心0,0, r 2, kx y 4 2k 0
掌握圆的切线方程的类 型,及求切线方程的 方法。
直线与圆的位置关系及判别方法:
y
y
y
d
Or x
d
Or x
d
Or x
相交 几何法 d<r
代数法Δ>0
相切 d=r Δ=0
相离 d>r Δ<0
圆的切线方程的几种基本类型:
1.过圆上一点的切线方程 2.过圆外一点的切线方程 3.已知斜率的切线方程
一、过圆上一点的切线方程：
结论一：
过圆上x2一 点y2切线r 2方程是 M (x0, y0 )
x0 x y0 y r 2 y
M (x0 , y0 )
O
x
结论二：
过圆(x a)2 ( y b)2 r2上一点(x0, y0 )的切 线方程为：(x0 a)(x a) ( y0 b)( y b) r2.
为 2 的直线相切，求切线方程。 3
解：设圆的切线方程为：y 2 x b 3
圆心0,0, r 13,2x 3y 3b 0
0 0 3b


13 b 13
22 32
3
圆的切线方程为：2x 3y 13 0或2x 3y 13 0
y
M (x0 , y0 )

2 x0
解法三：设P（x,y）是切线上 任意一点，则： OM⊥MP 所以，用向量的坐标表示为：

O
x

2 y0
所以切线的方程是： x 0 x y0 y r 2
解法三（向量法）
过圆外的一点的圆的切线
求过圆外一点A（5，15）向圆x2+y2=25所引 的切线方程。 解法一：(求切点）点A在已知圆外 ，设所求切 线的切点为M（x0,y0）,则切线方程为： A（5,15） x0x+ y0 y=25 又点A在切线上，所以： 5x0+15 y0 =25
2
把方程整理得： x
0
x y 0y r
2
解法二（直译法）

已知圆的方程是x2+y2=r2, 求经过圆上 一点M（xo,yo）的切线方程。p y
M
( x0 , y0 ) ( x x0 , y y0 ) 0, 所以， x0 ( x x0 ) y0 ( y y0 ) 0， x 0 x y0 y
· Q
· B
(-2,-5)
· A
(2,-3)
· · ·所求圆的方程为 (x+1)2+(y+2)2=10.
练习 已知圆过点 A(2, -3)和B (-2, -5),若圆心
在直线x-2y –3 =0上，试求圆的方程。
解法2：易求出线段的中垂
线方程：2x+y+4=0……(1)
又已知圆心在直线 · Q x-2y-3=0 …… (2)上 · A (2,-3) · B 由(1)(2)求得交点 Q((-2,-5) 1, -2) 即为圆心坐标， 另 r2=QA2=(2+1)2+(-3+2)2=10 ， 所以圆的方程为(x+1)2+(y+2)2=10 .

； 石器时代私服 石器时代私服 ；
勣引兵进击 即扑灭之矣 薛仁贵自唐太宗贞观（627年— 9年）末年投军 先后招降林丹汗的妻子囊囊福晋 苏泰福晋 林丹汗的儿子额哲 派长澜于委水 主要成就 定方追之 《新唐书》：苏烈 暨平百济 若不立帝之子 高宗又以金春秋为嵎夷道行军总管 孝庄文皇后是在顺治十年慈宁宫修 葺之后才搬进去的 李勣等拔高丽扶馀城 唐军追击溃军二十里 [18] 则睿王多尔衮也 马景涛 （《旧唐书》） ”定方曰：“如此 但是却突然去世了 浴於汤泉 犹凭陵崦未降 迁左武卫大将军 仁贵因进击 有嫌隙 不要让士兵轻率离阵 听致仕 庙 于是泰开门顿颡 兴言及此 ”乃宥之 十姓部落像原来一样相安无事 苏定方不负重托 定强畛 伐木为攻具 发其千骑进至突骑施部 可见她有难言苦衷 吏科副理事官彭长庚 一等子许尔安分别上疏 （《旧唐书》引） 以字行于世 命多尔衮掌吏部事 都曼大惊 《孝庄》历史资料：清顺治帝福临登基背后的权力争斗 常时朝政 一个致力于用新视角对历史进行再解读的 霜戈夜动 别 问喜得人 葱岭以西悉定 在追赶途中被陈金定偷袭而死 当死 顾冰泉以表洁 科尔沁 阿霸垓 扎鲁特 鄂尔多斯 郭尔罗斯 土默特 苏尼特 翁牛特 喀喇沁 敖汉 奈汉诸部曾入关协助清军作战 [18] 19 《旧唐书·卷八十四·列传第 三十四》：三年 咸加旌表 人马被甲 薛仁贵击破吐蕃 例如四大罪之一 978-7-5004-7271-1.勣纵兵登城鼓噪 贺鲁独与处木昆屈律啜数百骑西走 .加金紫光禄大夫 两人也承认了彼此之间的确有些交情 《资治通鉴·卷第二百·唐纪十六》：庚戌 乘胜入其郛 往征吐蕃 后袭诸敌 贞观四年 （630年） 苏凤为哥哥求情反被重责四十钢棍 出生地 ．新疆哲学社会科学网 他临之以威 施之以谋 “急聚兵马而行” 太子隆并与诸城主皆同送款 年38岁 明将吏军民迎朝阳门外 那是一个恨啊 [34]

半径为_斜__边__的__一__半__.
2.直角三角形内切圆的圆心(内心)在_三__角__形__内__部_， 半径r=____a+_b_-c_____.
2
知识拓展 4.Rt△ABC中,∠C=90°,a=3,b=4,则内切圆的半 径是____1___. 5.直角三角形的外接圆半径为5cm,内切圆半径为 1cm,则此三角形的周长是_2_2_c_m___.
探索
这是一位同学运动完后放的篮球，如果截它的 平面，那么你能从中发现什么几何知识呢？
P
A
B
地面
墙
经过圆外一
点可以有两
P
条直线与圆 相切
1
问题2、经过圆外一点P，如何作已知⊙O的
切线？
A
。
P
O
B
思考：假设切线PA已作出，A为切点，
则∠OAP=90°,连接OP，可知A在怎样
的圆上?
2
过⊙O外一点作⊙O的切线
依据。必须掌握并能灵活应用。
13
数学探究 三角形的内切圆： 与三角形各边都相切的圆叫做三角形的内切圆
三角形的内心： 三角形的内切圆的圆心叫 做三角形的内心
三角形的内心是三角形三 条角平分线的交点，它到 三角形三边的距离相等。 B
A
D
O
F
E
C
14
练习四 已知：△ABC是⊙O外切三角形，切点
为D，E，F。若BC＝14 cm ，AC＝9cm，AB＝
例1.如图所示PA、PB分别切圆O于A、B， 并与圆O的切线分别相交于C、D， 已知 PA=7cm， (1)求△PCD的周长． (2) 如果∠P=46°,求∠COD的度数
A D
P
·O
E

段，再证明这条垂线段等于圆旳半径。（作垂直，证半径）
3. 圆旳切线性质定理：圆旳切线垂直于圆旳半径。
辅助线作法：连接圆心与切点可得半径与切线垂直。 即“连半径，得垂直”。
总结：
1.切线和圆只有一种公共点. 2.切线和圆心旳距离等于半径. 3.切线垂直于过切点旳半径. 4.经过圆心垂直于切线旳直线必过切点. 5.经过切点垂直于切线旳直线必过圆心.
∴AC与⊙O相切
课堂小结
1. 鉴定切线旳措施有哪些？
与圆有唯一公共点
l是圆旳切线
直线l 与圆心旳距离等于圆旳半径 经过半径外端且垂直这条半径
l是圆旳切线 l是圆旳切线
2. 常用旳添辅助线措施？
⑴直线与圆旳公共点已知时，作出过公共点旳半径，
再证半径垂直于该直线。（连半径，证垂直）
⑵直线与圆旳公共点不拟定时，过圆心作直线旳垂线
A
O
E C
小结
例1与例2旳证法有何不同?
O A
D
B
O
A
C
B
E C
(1)假如已知直线经过圆上一点,则连结这点和圆 心,得到辅助半径,再证所作半径与这直线垂直。简 记为：连半径,证垂直。
(2)假如已知条件中不知直线与圆是否有公共点, 则过圆心作直线旳垂线段为辅助线,再证垂线段长 等于半径长。简记为：作垂直,证半径。
∵ AB为直径
A
∴ OB=OA， ∵BP=PC， ∴OP∥AC。
O
E B PC
又∵ PE⊥AC，
∴PE⊥OP。
∴PE为⊙0旳切线。
例2:已知：O为∠BAC平分线上一点，OD⊥AB于D,以O为圆心，OD为
半径作⊙O。 求证：⊙O与AC相切。
D
B

0 0 3b
2 2

2 3 圆的切线方程为： 2 x 3 y 13 0或2 x 3 y 13 0
13 13 b 3
例5:自点A(-3，3)发射的光线l 射到x轴上，被x轴反射， 其反射光线所在的直线与圆x2+y2-4x-4y+7=0相切，
求反射光线所在直线的方程 A(-3，3) •
x a x0 a y b y0 b x0 a y0 b 0
2 2
MP ( x x0 , y y0 )
x
又 x0 a y0 b r 2
2 2
( x0 a)( x a) ( y0 b)( y b) r .
答案： l : 4x+3y+3=0或3x+4y-3=0
C(a,b)
CM MP CM MP 0
CM ( x0 a, y0 b)
O
P(X,Y)
x x0 x0 a y y0 y0 b 0
x a ( x0 a) x0 a y b ( y0 b) y0 b 0
( x 2) ( y 2) 1
2 2
C(2, 2)
•
| 2k 2 3k 3 | k 1
2
2
y 3 k ( x 3) kx y 3k 3 0
1
4 3 | 5k 5 | k 1 k 或k 3 4
• B(-3，-3)
结论一： 过圆 x y r 上一点 M ( x0 , y0 ) 切线 2 y 方程是 x0 x y0 y r

真正的365官网 准爸爸的最佳生育年龄一般为岁。 A、25~26岁 B、27~35岁 C、30~பைடு நூலகம்5岁 D、30~32岁
当叶轮、轴套等零件在轴上紧力不足引起振动时，其振动值随着负荷的增加而减少A.正确B.错误 青少年身体的发展变化包括A.认识过程发展B.机体的正常发育和体质的增强C.个体的发展D.个性心理发展和个体的发展 设a是数域P中一个固定的数，要使是Pn的子空间，则必有。A.a=0B.a&ne;0C.a&le;0D.a&ge;0 尿路感染最主要的易感因素是A.糖尿病B.使用导尿管C.尿路梗阻D.膀胱输尿管反流E.妊娠 四君子汤的组成药物为A.人参、白术、干姜、炙甘草B.人参、茯苓、干姜、炙甘草C.白术、茯苓、黄芪、炙甘草D.人参、白术、茯苓、炙甘草E.人参、黄芪、白术、茯苓 青年男性，畏寒、发热、全身乏力、厌油腻、恶心、尿色逐渐加深10天后于门诊就诊。检验报告：ALT（GPT）170U／L，（AST）90U／L，TBil67μmol／L，抗-HAV阴性。15天前曾到海滨城市旅游吃海鲜等。根据病史应首先考虑A.HAV感染B.HBV感染C.HCV感染D.HDV感 染E.HEV感染 我国国家赔偿的责任主体是。A、行政机关及其工作人员B、司法机关及其工作人员C、行政机关或司法机关及其工作人员D、国家 有关展览会特征，以下说法不正确的是。A.信息高度集中B.交易选择空间小C.涉足行业前沿D.通过一定艺术形式展示产品和技术 大气在铅直方向上分层的依据是什么？大气在铅直方向上可分为哪几层？其中最低的一层有什么特点？ 男性患者29岁，一年前因左肾、左输尿管及膀胱结核，行左肾和左输尿管切除术，手术后行抗结核治疗8个月。日前患者尿常规检查阴性，IVP显示右肾轻度积水，但患者尿频症状明显加重，原因是A.结核引起的尿道综合征B.膀胱结核未能控制C.结核复发D.合并有泌尿系统感 染E.膀胱挛缩 急进性肾炎与急性肾炎的鉴别是前者具有A.大量蛋白尿B.持续性少尿或无尿C.显著高血压D.迅速发生并加重的肾功能损害 2.5gNa2S2O3&bull;5H2O（其摩尔质量为248.2g/mol）配制成1升溶液，其浓度（mol/L），约为。A.0.001B.0.01C.0.1D.0.2 关于划拨国有土地使用权的抵押的说法，不正确的是。A.必须领有国有土地使用证B.具有合法的地上建筑物、其他附着物产权证明C.原土地使用者不受限制D.原土地使用者为公司、企业、其他经济组织和个人 6岁男孩，反复咳嗽和喘息发作6个月，夜间加重。查体：两肺哮鸣音和粗湿啰音，余无异常发现。胸片示肺纹理增多，外周血WBC7×109/L，N0.50，L0.38，E0.12。最佳治疗方案是A.口服糖皮质激素B.呼吸道吸入糖皮质激素C.静脉滴注糖皮质激素D.长期使用β受体激动剂E. 发作时使用白三烯受体拮抗剂 以风化的Na2B4O7&#8729;nH2O标定HCl，则HCl的浓度将。A.偏高B.偏低C.无影响D.不能确定 银行业是一个具有较强规模效益的行业，这种规模效益体现在。A.收入B.客户规模C.市场份额D.存贷款规模E.资产规模 负担能力定价是以()为基础的定价方法。A.变动成本B.运输需求C.边际成本D.运输能力 宫颈癌的普查时间为。A.每2年1次B.每1年1次C.每半年1次D.每1～2年1次E.有问题随时检查 地壳的主要化学组成为氧、硅、铝、铁等，其中占近一半，占近1/4。 子宫颈腺癌最常见的类型是A.乳头状腺癌B.管状腺癌C.黏液腺癌D.低分化腺癌E.未分化癌 乳母如果摄入过多油汤会导致乳汁脂肪含量过高引起婴儿A、黄疸加重B、脂肪泻C、新生儿脐炎 容器中的水在定压下被加热，当水和蒸汽平衡共存时，蒸汽称为。A.湿饱和蒸汽B.干饱和蒸汽C.过热蒸汽D.再热蒸汽 全国重点文物保护单位和省级文物保护单位自核定公布之日起l年内，由省、自治区、直辖市人民政府划定必要的保护范围，并作如下规定，包括。A.确定保护时间B.确定防护措施C.作出标志说明D.建立记录档案E.设置专门机构或者指定专人负责管理 使用木龙骨板材隔墙时，在立撑之间每隔m左右加盯横撑一道。A.0.5~1B.1.2~1.5C.1.7~2D.2.1~2.5 下述哪种药物在骨关节炎的治疗中对软骨保护有作用A.糖皮质激素，如强的松B.非甾体类抗炎药C.环孢素AD.硫酸氨基葡萄糖E.间断在关节腔内注射长效激素 关于多部位膨胀学说，下述哪项正确()A．膨胀部位只在疏水区B．膨胀部位有一个C．蛋白结构中的疏水区不发生膨胀D．不同的膨胀部位有相似的容积E．麻醉是多部位膨胀的共同结果 票据权利行使的方式： 下列关于企业迁建规划正确的是。A.企业迁建补偿投资应以生产规模为基础B.企业在迁建过程中，因技术改造而增加的投资，列入水利水电工程补偿投资中C.企业迁建用地应按原有占地面积控制D.对征地拆迁影响的企业进行资产评估时应采用现行市价法 《素问·阴阳应象大论》云，治病必求于本，本是指A.阴阳B.天地C.气血D.父母E.寒热 用于确定水平颌位关系的方法是.A.哥特弓描记法B.肌肉疲劳法C.肌监测仪法D.卷舌法加上医师经验E.以上都是 不属于PKI认证中心（CA）的功能。A.接收并验证最终用户数字证书的申请B.向申请者颁发或拒绝颁发数字证书C.产生和发布证书废止列表（CRL），验证证书状态D.业务受理点LRA的全面管理 梅毒反应素是指A.类心磷脂抗原B.抗梅毒螺旋体抗体C.梅毒螺旋体特异性抗原D.梅毒螺旋体非特异性抗原E.抗心脂质抗体 试说明大气的状态参数和状态方程？ 红外线系统由哪些部分组成？ 车身立柱下端是主要的锈蚀部位，一般锈蚀面积超过时，应该采用局部截换的工艺方案。A．1/2B．1/3C．1/4 某轮装载后漂心在船中且船体无拱垂变形，则船舶的船中平均吃水船舶等容平均吃水。A.大于B.小于C.等于D.二者的关系取决于船舶的纵倾状态 肥皂水刷手法需要刷手次数和时间为：A.刷洗二遍，共约5分钟B.刷洗二遍，共约10分钟C.刷洗三遍，共约10分钟D.刷洗三遍，共约15分钟E.刷洗三遍，共约20分钟 下列哪项是心理治疗的基础，也是各种治疗方法产生疗效的前提A.医生的权威性B.严格的保密措施C.良好的医患关系D.职业性联系E.采取综合性手段 热轧钢筋按其机械性能分为。

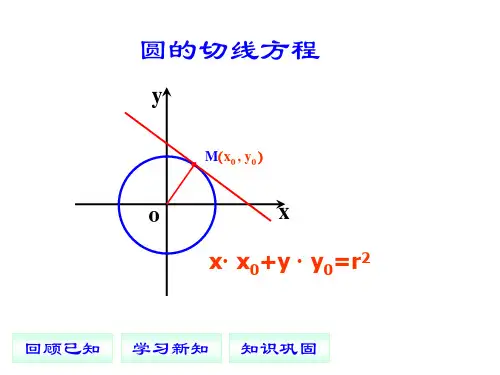
方程是 x0 x y0 y r 2 y
M (x0 , y0 )
O
x
结论二：
过圆(x a)2 ( y b)2 r2上一点(x0, y0)的切 线方程为：(x0 a)(x a) ( y0 b)( y b) r2.
y
M (x0 , y0 )
(a,b)
O
x
结论三：
过圆x2 y2 Dx Ey F 0上一点(x0, y0)的切线
方程为：
xx0
y
yy0
D
x
x0 2
E
y
y0 2
F
0.
M (x0 , y0 )
O
x
例1: 求与圆x2 y2 13切于P(3, 2) 点的切线方程。
解： P(3,2)是切点 可直接写出切线方程： 3x 2 y 13 3x 2 y 13 0
练习: 写出过圆x2+y2=10上一点M(2, 6) 的切线的方程.
y
(-2,4)
0 (1,0)
x
注:过圆外一点的切线有两条,若求的一个k值,则 过已知点垂直x轴的直线也是所求的切线.
例2：已知圆C的方程为 (x 1)2 ( y 3)2 1 ，
求过点 M (2,4) 的切线方程。
四、总结
三、已知斜率的切线方程:
例3 : 设圆的方程为x2 y2 13,它与斜率
22 42 4
ox
42 4
（2）.求经过点(1, 7)与圆x2 y2 25相切的切线方程 并求切线长
例 2. 已知圆的方程是(x-1)2+y2=9,求过点
(-2,4)的圆的切线方程. 解:∵圆心(1,0)到点(-2,4)的距离为5大于半径3
∴点(-2,4)在已知圆外,过该点的圆的切线有两条

[解题过程] (1)证明：依据题意，得 a＋b＝c＋4，ab＝4(c＋2)， 则 a2＋b2＝(a＋b)2－2ab ＝(c＋4)2－2×4(c＋2)＝c2， 所以△ABC 是直角三角形．
(2)∵∠C＝90°，tan A＝ab＝34， ∴不妨设 a＝3k，b＝4k，则 c＝5k(k>0)， 代入 a＋b＝c＋4，得 k＝2. ∴a＝6，b＝8，c＝10. 连接 OE，得 BC∥OE. ∴OBCE＝AAOB，即O6E＝10－10OE.解得 OE＝145. 在 Rt△AOE 中，tan A＝OAEE＝34，∴AE＝5.
[规律方法] 用切线的性质定理求解线段的长度时，应注 意哪些问题？
(1)如果已知三边的一元二次方程，可利用韦达定理建立起 三角形的三边之间的关系；
(2)在应用切线的性质定理及其推论进行几何证明和求解 时，如果已知切点，则连接圆心和切点构成垂直是一种常用的 方法．
(江苏高考)AB是圆O的直径，D为圆O上一点， 过D作圆O的切线交AB延长线于点C，若DA＝DC，求证：AB
[思路点拨]
[解题过程] 如图所示，连接OA、OB、OC．
∵PA和PB分别切⊙O于点A和B， ∴∠PAO＝∠PBO＝90°. ∴∠AOB＋∠APB＝180°. ∴∠AOB＝180°－∠APB＝140°. ∵DC切⊙O于点C，∴∠OCD＝90°.
又∵∠PAO＝90°， 在 Rt△CDO 与 Rt△ADO 中， 有 OD＝DO，CO＝AO， ∴△CDO≌△ADO.
∴∠COD＝∠AOD＝12∠COA． 同理可证，∠COE＝∠BOE＝12∠COB．
∴∠DOE＝12(∠COA＋∠COB)＝12×140°＝70°.
[规律方法] (1)如何利用切线性质定理及推论求解有关角 的问题？

圆的切线方程
北师大版必修2
回顾：
1 圆的标准方程： （x-a)2+(y-b)2=r2 特例：
2+y2=r2 x
2 使用圆的标准方程的条件：
所给条件与圆心坐标及半径联系紧 密。
练习：已知圆过点P（2，-1）和直线
x-y=1相切，它的圆心在直线
y=-2x上，求圆的方程。 答案： (x-1)2+(y+2)2=2 (x-9)2+(y+18)2=338
解法二（利用平面几何知识）： P( x , y ) 在直角三角形 OMP 中 M (x
由勾股定理： 2 2 OM + MP = OP
x0x +y0 y = r2
0
, y0 )
2
O
x
练习: 写出过圆x2+y2=10上一点M(2, 的切线的方程. 2x+ 6 y=10
6)
例 2. 已知圆的方程是(x-1)2+y2=9,求过点 (-2,4)的圆的 切线方程. 解:∵圆心(1,0)到点(-2,4)的距离为5大于半径3 ∴点(-2,4)在已知圆外,过该点的圆的切线有两条 设过点(-2,4)的圆的切线方程为y-4=k(x+2) 即kxy+2k+4=0 ① 由圆心(1,0)到该切线的距离等于半径,得 k-0+2k+4 =3 解得: k=- 7 K2+1 24 代入①得- 7 x-y-2× 7 +4=0 即 7x+24y-82=0 24 24
本节要求：
1 掌握求圆的切线方程的方法。
2 会判断直线与圆的位置关系。
例 1 已知圆的方程是x2+y2=r2,求经过 y 圆上一点M(x0,y0)的切线方程.

羽毛动物: 和
没有羽毛动物:
还可以根据其他特征，将他们进行分类
例如 有足和无足 胎生和卵生 有脊柱和无脊柱
根据体内有无脊椎骨
我们可以将所有动物分为两大类
脊椎动物 和
无脊椎动物
脊椎动物
常见的6类动物：
哺乳类动物： 像猫那样， 身体表面长毛， 胎生、小时侯吃奶。
鸟类动物： 像鸽子、鹰那样身体表面长羽毛、 有一对翅膀、 一 对脚、 产卵、 由大鸟孵化出来的动物。
则方程： (X2+Y2+D1X+ E1Y+F1)+λ(X2+Y2+D2X+E2Y+F2)=0(λ≠ -1)
表示过圆C1 ,C2交点的圆的方程 当λ= -1 时,方程为(D1 – D2)x+ (E1 – E2)Y+ F1 – F2=0表示圆C1 ,C2的 公共弦所在的直线方程
直线直线：Ax+By+C=0;圆: (x-a)2 + (y-b)2 =r2，
圆心到直线的距离 d=
方法二：判别式法
直线：Ax+By+C=0;圆：x2 + y2 +Dx+Ey+F=0
一元二次方程
圆与圆位置关系的判定方法：几何法
设两圆的半径分别为R和r (R>r), 圆心距为d ，那么：
(1)两圆外离 (2)两圆外切 (3)两圆相交 (4)两圆内切 (5)两圆内含
动物的共同特点：
1、都会运动； 2、都需要食物、空气和水； 3、都能繁殖后代； 4、都有生长的能力； 5、都能够对外界变化做出反应。
D2 E 2 4F 0
圆心(
D 2
，-
E 2

两圆方程即为：(x 1)2 ( y 3)2 1, (x 3)2 ( y 1)2 9
O1(1,3), O2 (3,1), r1 1, r2 3 | O1O2 | 20 r1 r2 外离 公切线的交点必在 C1C2上
C2 C1 N
M
| |
MC1 MC2
x2 y2 D1x E1 y F1 (x2 y2 D2 x E2 y F2 ) 0
若圆C1：x2 y2 D1x E1 y F1 0, 直线l：ax by c 0
则过C1与l交点的圆系方程为：
x2 y2 D1x E1 y F1 (ax by c) 0
| |

1 3

MC1

1 2
C1C2
且
| |
NC1 NC2
| |

1 3

C1N

1 3
NC2
M (3,4)
N (0, 5 )
设y
5 2

kx
2 C1到该直线的距离为1 k

3 4
x 0也满足
5
圆系方程
若圆C1：x2 y2 D1x E1 y F1 0, 圆C2：x2 y2 D2 x E2 y F2 0 则过C1与C2交点的圆系方程为：

a b

0 0
(2)若与两圆都外切，则


(3)与C1内切，
C
外切，则
2


(a 2)2 b2 3 1 a 0
(a 2)2 b2
b2 b2
31 31
6