伯努利方程
- 格式:ppt
- 大小:2.13 MB
- 文档页数:38

伯努利流体方程
伯努利方程(Bernoulli's equation)是流体力学基本方程之一,常用于描述静止流体或运动流体在流经不同位置时,压力、速度、高度等物理量的变化关系。
伯努利方程最早由瑞士数学家和物理学家伯努利(Daniel Bernoulli)在1738年提出,被称
为伯努利定理,也称作伯努利方程或伯努利流体方程。
伯努利方程的数学形式为:
P + 1/2ρv^2 + ρgh = constant
其中,P表示流体的压力,ρ表示流体的密度,v表示流体的
速度,g表示重力加速度,h表示流体的高度,constant表示一个常数。
伯努利方程可以表达出一个流体在液体静压力、动能和势能三者之间的平衡状态。
在一个理想的流体中,如果流体穿过一段水管,那么在这段水管的任何位置,液体静压力、动能和势能总和相等。
应用伯努利方程,可以计算液体在不同位置的压力、速度和高度等物理量的变化。
伯努利方程可以应用在气体、液体等不同介质的流体力学问题中,如风力发电机、水压机等。

伯努利方程三种形式公式
第一种形式的伯努利方程公式是:
P₁ + 1/2ρv₁² + ρgh₁ = P₂ + 1/2ρv₂² + ρgh₂
其中P₁和P₂分别表示两个位置的压力,ρ表示流体的密度,v₁和v₂表示两个位置的流速,g为重力加速度,h₁和h₂表示两个位置的高度。
这个公式描述了流体在两个位置之间能量守恒的关系。
等式左边的第
一项表示压力能,第二项表示动能,第三项表示单位质量的重力势能。
等
式右边的三项表示相应位置的压力能、动能和重力势能。
这个公式适用于
流体在不完全关闭的管道、管道两端处于同一高度的情况。
第二种形式的伯努利方程公式是:
P + 1/2ρv² + ρgh = const
这是一个简化形式的伯努利方程,它将两个位置的参数合并成一个常数。
这个公式的物理意义是,当流体在流动过程中没有受到外界力的作用时,流体的总能量保持不变。
这个公式适用于理想的水平管道、无摩擦的
流动。
第三种形式的伯努利方程公式是:
P + 1/2ρv² = const
这是伯努利方程的最简形式,它忽略了重力势能的影响。
这个公式适
用于理想的非粘性流体在无重力情况下的流动,如气体等。
这三种形式的伯努利方程公式分别适用于不同的流体力学问题。
选择
适用的公式取决于具体的流动条件和需要分析的问题。
无论选择哪种形式,
伯努利方程都提供了一个重要的工具,可以帮助我们研究流体力学中的能量转换和守恒。

伯努利方程伯努利方程是描述理想流动的基本方程之一,它是在瑞士数学家伯努利(James Bernoulli)在1738年发表的一篇论文中提出的。
该方程对于理解流体力学以及飞行、水力、空气动力学等领域具有重要的应用。
伯努利方程是基于质量守恒定律、动量守恒定律和能量守恒定律推导而来的方程。
该方程表达式为:P + ½ρv² + ρgh = 常数其中,P为流体的压力,ρ为流体的密度,v为流体的速度,h为流体的高度,g为重力加速度。
伯努利方程是在假设部分没有粘性损失的情况下成立的,也就是无黏性流动。
在实际的情况下,流体会存在一定的粘性损失,因此伯努利方程只适用于无粘流体,但在低速流动下,伯努利方程可近似地应用于粘性流体。
对于伯努利方程,我们可以从以下角度来解释其中的每个项:① P:压力项,它表示了流体在流动过程中所受到的压力。
当流体速度增加时,压力往往会降低,例如在突缩管中,当管道的截面积变小时,流体的速度会增加,而压力会降低。
②½ρv²:动能项,它表示了流体的动能。
在流体的流动过程中,当速度增加时,动能也会增加,例如在水力发电站中,当水流的速度增加时,水的动能也会增加,从而推动水轮发电。
③ρgh:势能项,它表示了流体的势能。
当流体在重力作用下流动时,流体会从高处向低处移动,势能也随之降低。
例如当我们用pump把水从低处抽到高处时,水的势能就会增加。
由于伯努利方程中的常数在同一条流线上保持不变,因此可以利用伯努利方程来分析流体在不同位置的流速、压力和高度之间的关系。
这在飞行、水利及空气动力学等领域的设计和应用中具有重要的作用。
伯努利方程的应用十分广泛。
例如在空气动力学领域中,伯努利方程被用来解释飞机起飞、飞行、着陆过程中的颤振等现象。
在水利工程领域中,伯努利方程被用来计算水流在不同地方的速度、压力和高度等因素,对于设计水坝、水龙头、流量计等工程设施具有重要的作用。
总之,伯努利方程作为理解流体力学基本方程之一,不仅在理论研究中具有广泛的应用,也在实际的设计和应用中具有十分重要的意义。

伯努利方程计算
伯努利方程是应用于流体力学和气体流动的基本方程之一,用于描述沿流体流动方向上的动能、压力和重力势能之间的关系。
伯努利方程可以用以下的数学形式表示:
P + 1/2 ρv² + ρgh = constant
其中,P表示流体的压力,ρ表示流体的密度,v表示流体的
流速,g表示重力加速度,h表示流体的高度。
伯努利方程适用于理想流体在稳定流动时,沿着流动方向,流速变化不大,流线不弯曲,且没有其他外力作用的情况下。
利用伯努利方程可以计算流体在不同位置处的压力和流速。
通过等式中的常数项,可以比较不同位置处的流体状态。
需要注意的是,伯努利方程忽略了一些现实流动的因素,如黏性、湍流和摩擦等,因此只适用于某些特定情况。
在实际应用中,伯努利方程常用于气候学、飞行器设计、水力学、管道流动等领域的计算和分析。

伯努利方程中表示
伯努利方程:p+ρgz+(1/2)*ρv^2=C。
式中p、ρ、v分别为流体的压强、密度和速度;z 为铅垂高度;g为重力加速度.
上式各项分别表示单位体积流体的压力能p、重力势能ρg z和动能(1/2)*ρv ^2,在沿流线运动过程中,总和保持不变,即总能量守恒.但各流线之间总能量(即上式中的常量值)可能不同.对于气体,可忽略重力,方程简化为p+(1/2)*ρv ^2=常量(p0),各项分别称为静压、动压和总压.显然,流动中速度增大,压强就减小;速度减小,压强就增大;速度降为零,压强就达到最大(理论上应等于总压)。
伯努利方程中各项意义如下:
1、理想流体定常流动的动力学方程。
意思为流体在忽略粘性损失的流动中,流线上任意两点的压力势能,动能与位势能的和保持不变。
2、方程中的符号分别表示流体的压强,密度和速度。
剩余符号表示铅垂高度和重力加速度。
同时各项分别表示流体的压力能和重力势能和动能。
3、能量守恒定律在理想流体定常流动中的表现。
它是流体力学的基本规律。
在一条流线上流体质点的机械能守恒是伯努利方程的物理意义。



伯努利方程公式单位伯努利方程可是流体力学中的一个重要家伙呀!它描述了在理想流体沿着一条流线流动时,压力、速度和高度之间的关系。
伯努利方程的公式是:$p + \frac{1}{2}\rho v^2 + \rho gh = 常量$ 这里的“p”表示压强,单位是帕斯卡(Pa);“$\rho$”是流体的密度,单位通常是千克每立方米(kg/m³);“v”代表流体的速度,单位是米每秒(m/s);“g”是重力加速度,一般取值 9.8 米每二次方秒(m/s²);“h”表示高度,单位是米(m)。
我记得有一次给学生们讲这个伯努利方程的时候,那场面可有趣啦!当时我拿着一个 U 型管,里面装着有色的液体,然后用吹风机对着 U型管的一侧吹风。
孩子们都瞪大眼睛看着,充满了好奇。
我就问他们:“猜猜看,这液体的高度会怎么变化?”有的孩子说会升高,有的说会降低,还有的一脸迷茫。
我接着给他们解释伯努利方程,告诉他们风一吹,这一侧的速度变快了,根据方程,压强就会变小,所以另一侧的液体就会被压过来,这边的液面就升高啦。
孩子们恍然大悟的表情,让我特别有成就感。
在实际生活中,伯努利方程的应用那可真是无处不在。
比如说飞机的机翼,上面是弧形,下面是平的。
当飞机飞行时,空气在上面流动的路程长,速度就快,压强小;下面空气流动路程短,速度慢,压强大,这样就产生了向上的升力,飞机才能飞起来。
还有我们家里用的喷雾器,当我们按压喷头时,里面的液体流速加快,压强减小,外面的大气压就把液体压成雾状喷出来了。
再比如足球比赛中的“香蕉球”,运动员踢球时让球旋转起来,一侧的空气流速快,压强小,另一侧压强大,球就会在空中划出一道弯曲的弧线。
伯努利方程不仅仅是一个公式,它更是我们理解和解释很多自然现象和工程应用的有力工具。
无论是小小的喷雾器,还是大大的飞机,都离不开这个神奇的方程。
学习伯努利方程,让我们能更好地理解这个世界,发现那些隐藏在日常生活中的科学奥秘。

伯努利方程常微分方程
伯努利方程是一种常微分方程,是数学中比较重要的方程类型之一。
它在理论研究和应用上都具有非常重要的作用,是数学研究和物
理应用的基础。
伯努利方程的形式是dy/dx + P(x)y = Q(x)y^n,其中P(x)和Q(x)都是已知函数,n是实数。
伯努利方程是一种特殊的非线性方程,因为它的非线性项y^n与y的一次项dy/dx组合在一起。
伯努利方程的解法有很多,其中比较常用的方法是变量代换和分
离变量法。
变量代换的思想是将伯努利方程中的非线性项y^n用另一
个变量z来代换,从而将伯努利方程转化为一般的一阶线性方程。
分
离变量法则是通过将方程中的y和dy/dx分离,从而可以得到y的解
析表达式。
伯努利方程在物理学中的应用也非常广泛。
例如,在空气动力学中,它可以用来描述流体的运动和压力分布。
在生物学中,它可以用
来描述人体器官的运动和生理过程。
在经济学中,它可以用来描述市
场供需的关系和价格变化。
因此,了解伯努利方程的解法和应用对于
理解和掌握这些领域的知识都具有非常重要的指导意义。
总之,伯努利方程是一种具有重要理论和应用价值的常微分方程,是数学、物理、生物、经济等多个领域的基础和核心概念之一。
掌握
伯努利方程的解法和应用对于学术研究和实际应用都具有非常重要的
意义。

伯努利原理公式伯努利原理往往被表述为p+1/2ρv2+ρgh=C,这个式子被称为伯努利方程。
式中p为流体中某点的压强,v为流体该点的流速,ρ为流体密度,g为重力加速度,h为该点所在高度,C是一个常量。
它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。
伯努利方程是丹尼尔•伯努利在 1726 年研究理想液体作稳定流动时提出的。
静压是流体真实存在的压强值,动压也称为速压或速度头,其单位也是Pa。
动压起到调节静压在总压中所占比例的作用:动压越大,静压越小;动压越小,静压越大;动压为零时,即流速为零,静压最大且等于总压值。
因此,伯努利方程式的物理含义也可以说成是流体的压强能和动能之间可以相互转化,但流动的总机械能保持不变。
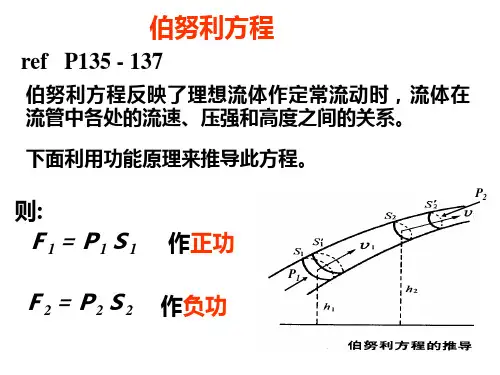
伯努利方程是流体力学的基本方程,它反映了理想液体作稳定流动时,压强、流速和高度三者之间的关系。
答案】一、一般条件下伯努利方程在各项的意义P +1/2ρv2 +ρgh = 常量该方程说明理想流体在流管中作稳定流动时,单位体积的动能1/2ρv2 、重力势能ρgh 、该点的压强P 之和为一个常量.其中1/2ρv2相与流速有关,常称为动压,ρgh 和P 相与流速无关,常称为静压.二、单位重量流体中伯努利方程各项的物理意义ρg =m/u g =mg/u表示单位体积的重力,以ρg 除各项得:p/ρg+v平方/2 g+ h = 常量该方程表示流场中一点上单位重量流体所具有的总机械能. 其中p/ρg表示流场中一点上单位重量流体所具有的压力潜能,也就是压力对单位体积重量流体所做的功,v平方/2 g 表示单位重量流体所具有的动能, h 就是流场中该点的高度.由于v平方/2 g+ p/ρg+ z = 常数,定理中每一项都具有长度的量纲. 所以p/ρg 表示所考察点的压力潜能的同时也可表示它能将流体压升到某一高度的能力.三、单位质量流体中伯努利方程p/ρ项的物理意义以ρ除各项得:p/ρ+1/2 v平方 + gh = 常量该方程中:p/ρ项表示流场中某一点上单位质量流体所具有的压力或弹性势能,从能量的角度讨论p/ρ项也可理解为单位质量流体相对于p = 0 状态所蕴涵的能量.综上所述:通过以上的分析推导可以看出伯努利方程是能量方程式,尽管分析问题所用的动力学原理不同,但导出方程的意义是完全相同的,说明在管内作稳定流动的理想液体具有压力能、势能和动能三种形式的能量,在适合限定条件的情况下,流场中的三种能量都可以相互转换,但其总和却保持不变,这三种能量统称为机械能. 由此可以得出:伯努利方程在本质上是机械能的转换与守恒.。
伯努利方程高数
伯努利方程是一种常微分方程,它可以用来描述一个物体在某一时刻的变化情况,它的一般形式为:
\frac{dy}{dt}=f(y,t)
其中,y表示物体的状态变量,t表示时间,f(y,t)表示物体在时刻t时的变化率。
解伯努利方程的方法有很多,其中最常用的是高数方法。
高数方法是指将伯努利方程化为一个积分方程,然后用积分的方法求解。
例如,设伯努利方程为:
\frac{dy}{dt}=y^2-t^2
将其化为积分方程:
\int \frac{dy}{y^2-t^2}=\int dt
用积分的方法求解:
\frac{1}{2}\ln|y^2-t^2|=t+C
其中C为积分常数。
最后,将C代入上式,得到:
y^2-t^2=e^{2(t+C)}
即:
y=\pm \sqrt{e^{2(t+C)}+t^2}。
伯努利方程介绍
伯努利方程是流体力学中一个重要的方程,它描述了流体在运动过程中压强、速度和密度之间的关系。
在流体的运动过程中,伯努利方程可以表示为:p1 + ρ1(v1)^2/2 + g1z1 = p2 + ρ2(v2)^2/2 + g2z2。
其中,p1和p2分别表示流体的压强,ρ1和ρ2分别表示流体的密度,v1和v2分别表示流体的速度,g1和g2分别表示流体的重力加速度,z1和z2分别表示流体的位置高度。
在伯努利方程中,等号左边表示流体的总能量(包括压能和动能),等号右边表示流体的总能量(也包括压能和动能)。
因此,伯努利方程描述的是流体在运动过程中能量的守恒。
在流体运动中,伯努利方程具有非常广泛的应用。
例如,在管道中流动的流体,如果管道截面突然变小,流体的速度会增加,而压强会减小。
这是因为流体的总能量是守恒的,当管道截面变小时,流体的流速会增加,动能增加,而压能减小。
因此,伯努利方程可以帮助我们理解和预测流体运动中的各种现象。
此外,伯努利方程还可以用于解释飞机飞行的原理。
当飞机在空中飞行时,机翼上方的空气流速大于下方的空气流速,导致机翼上方的压强小于下方的压强,从而产生向上的升力。
这也是伯努利方程的应用之一。
总之,伯努利方程是流体力学中的一个重要方程,它描述了流体在运动过程中能量的守恒。
通过理解和掌握伯努利方程,我们可以更好地理解流体运动中的各种现象,并为实际应用提供重要的理论支持。
伯努利方程知识点伯努利方程是流体力学中最重要的方程之一。
它描述了沿流体流动方向的速度变化、压力变化以及液体高度的变化之间的关系。
伯努利方程在解决各种流体问题时都起着重要的作用,例如管道流动、飞行器设计和气象学等。
伯努利方程表示为:[ P + v^2 + gh = ]其中,P是流体的压力,ρ是流体的密度,v是流体的速度,g是重力加速度,h是流体的高度。
这个方程可以从动能定理、连续性方程和静力学平衡等基本原理推导出来。
接下来,我们将逐步解释伯努利方程的各个部分。
1.压力项(P):压力是流体分子对容器壁或其他物体施加的力。
在伯努利方程中,压力项表示流体的动能转化为静能的过程中产生的压力变化。
2.动能项:动能项((v^2))表示流体的动能,其中ρ是流体的密度,v是流体的速度。
这一项表示流体速度的平方与流体密度的乘积,即动能密度。
当流体速度增加时,动能项也会增加。
3.重力项:重力项((gh))表示流体由于高度变化而产生的重力势能。
ρ是流体的密度,g是重力加速度,h是流体的高度。
当流体高度增加时,重力项也会增加。
4.常数项:伯努利方程右侧的常数项表示在流体流动过程中保持不变的量。
这个常数可以代表某个特定位置的流体状态,或者是在某个位置上的初始状态。
伯努利方程的应用非常广泛,下面我们将通过几个具体的例子来说明。
1.管道流动:伯努利方程可以用来分析管道内的液体或气体流动。
当液体或气体通过管道时,速度、压力和高度会发生变化。
通过应用伯努利方程,我们可以计算出流体在不同位置上的压力或速度。
2.飞行器设计:伯努利方程在飞行器的设计中起着重要作用。
例如,在飞机的机翼上方存在着较快的气流速度,而底部的气流速度较慢。
根据伯努利方程,较快的气流速度会导致较低的气压,而较慢的气流速度会导致较高的气压。
这种压差会产生升力,使飞机能够飞行。
3.气象学:伯努利方程也可以用来解释气象现象。
例如,当风穿过山谷或峡谷时,由于流速增加,气压会降低。