第三章2伯努利方程及其工程应用

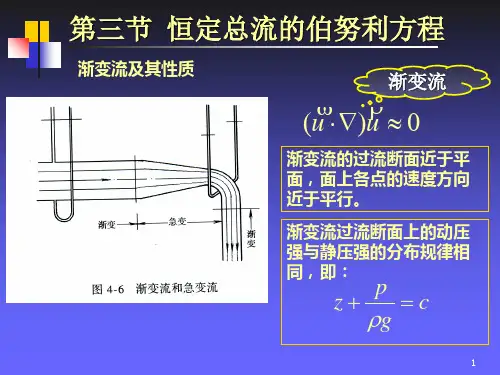
伯努利方程原理及其应用伯努利方程是流体力学中的重要原理之一，描述了沿着流体流动方向的速度、压力和高度之间的关系。

该方程是瑞士科学家丹尼尔·伯努利在18世纪中叶所提出的，并以他的名字命名。

伯努利方程原理基于流体的连续性和能量守恒定律，可以用来解决许多与流动相关的问题。

其基本形式可以表示为：P + 1/2ρv^2 + ρgh =常数其中，P表示压力，ρ表示流体的密度，v表示流体的速度，h表示流体的高度，g表示重力加速度。

此方程表明，在沿着流体流动方向的区域中，压力、速度和高度之间存在一种平衡关系，当一方发生变化时，其他两方也会随之发生相应的变化。

伯努利方程的应用非常广泛，下面我们将介绍其在多个领域中的具体应用。

1.液体流动伯努利方程可以应用于液体在管道和河流中的流动问题。

例如，在水力工程中，可以根据伯努利方程来计算水的压力和速度，从而确定水流是否顺畅。

此外，伯努利方程还可以应用于液体泵抽水的计算和涡轮机工作原理的分析，以及血液在动脉和静脉中的流动研究等。

2.汽车空气动力学伯努利方程在汽车设计中有重要的应用。

例如，在高速行驶时，汽车前进方向上的气流速度会增加，根据伯努利方程，气流速度增加就意味着压力降低。

这就解释了为什么汽车行驶时，车顶、车窗等地方的压力较低，从而产生了吸力，有利于汽车行驶稳定。

3.飞行器气动力学伯努利方程在飞行器气动力学中的应用非常重要。

在飞行过程中，飞机可以通过改变机翼形状和改变进气口的面积来调节气流速度和压力的分布，从而实现升力和稳定性的控制。

伯努利方程提供了一种描述飞行器气动表现的重要工具。

4.涡旋产生与气旋的形成伯努利方程也可以解释涡旋的产生和气旋的形成。

当流体经过结构物表面或物体尖部时，流体速度会增加，从而使压力降低。

这种速度增加和压力降低导致了涡旋产生。

类似地，大气中气流速度和气压的变化也会导致气旋的形成。

伯努利方程的应用还远不止于上述几个领域，例如喷射器的工作原理、风力发电工程中的风能转换等。

第30卷　第7期2001年7月 中学物理教学参考Ph ysics T each ing in M iddle Schoo l Vo l.30　No.7J u l.2001●教材教法●伯努利及伯努利方程的应用余学昌(河南省罗山县高级中学　464200) 高中《物理》(试验必修)教材中,增加了伯努利方程为选学内容.笔者在此对伯努利与伯努利方程的运用略作介绍如下.一、伯努利与伯努利方程1700年1月29日,伯努利出生于瑞士尼德兰的格罗宁根.他曾在海得尔贝格斯脱思堡和巴塞尔等大学学习哲学、伦理学、医学. 1721年取得医学硕士学位.在1725～1732年,伯努利在圣彼得堡大学教数学.1733年他担任巴塞尔大学解剖学教授,1750年成为物理学教授.他不仅是一位物理学家,还是一位数学家.18世40年代末,他出版了著名的著作《流体力学》一书.书中用能量守恒定律解决流体的流动问题,他分析流体流动时压强和流速的关系并得出方程,这就是后来以他的名字命名的“伯努利方程”.书中伯努利还明确叙述了分子动理论,认为气体作用在器壁上压力可以用大量的分子快速来回运动来解释.他还发表了海水潮汐、弦振动问题等论文.在有关微积分、微元方程和概率论等数学方面,他也做出了卓越的贡献.在1725～1749年期间,伯努利曾十次荣获法国科学院年度奖.1782年3月17日,伯努利在瑞士巴塞尔逝世.伯努利通过实验得出:理想流体在做稳定流动时,流速大的地方压强小,流速小的地方压强大(但并非反比关系).其数学表达式为p+Θv2�2+Θg h=常量.(推导见课本,这里从略)这就是著名的伯努利方程.二、伯努利方程的应用在日常生活和工程技术方面,伯努利方程的应用非常广泛正因如此,将这部分知识写进教材内容,体现了编者的独具匠心之处.下面笔者介绍几种比较重要的和常见的应用.11确定静止液面下深度为h处的压强如图1所示,在装着液体的容器里取液面图1上的点A和在液面下深h处的点B来研究.以点B处的水平面作为零(势能)参考面,则h A=h,h B=0,p A=p0,又因液体静止,v1=v2=0,代入伯努利方程,得p B=p A+Θg h=p0+Θg h.21计算液体从小孔中流出的流速设在液面下深为h的容器壁上有一小孔,图2液体从小孔中流出,如图2所示.取在液面上点A和小孔处点B来研究,因为容器的截面比小孔的截面大得多,所以容器中水面的下降很慢,点A处的液体微粒的流速可以不计,即v A=0,以点B处高度为零,则h A=h,h B=0,点A、B处与大气接触,所以p A=p B=p0(大气压),代入伯努利方程,得p0+Θg h=p0+12Θv B2,即v B=2g h.任何液体质粒从小孔中流出的速度与它由高度h处自由落下的速度相等.31测量流体的流速测量流体在管里的流速时,可用如图3所示的仪器,因它常用来测量气流速度,所以又叫做气流速度计分别把必多管(必多管是..A12一根一端封闭的弯管,封闭端A 光滑微尖,并图3在靠近封闭端的侧面上开着很多的小孔)和一个管口朝向气流的管子B (动压管)接在U 形管压强计上,根据U 形管两边的液柱的高度差便可求出气体的流速.假设气体稳定流动的速度是v ,气体的密度是Θ,压强计内液体的密度是Θ0,在管A 上小孔处气体的压强是p A ,管B 中气体的压强是p B ,管B 中气体因受管里液体的阻碍,它的流速等于零,由于管A 与管B 的端口均在同一高度上且处于气体的流动的同一流线上,根据伯努利方程,得p A -Θv 2�2=p B +0,故p B -p A =Θv 2�2.根据U 形管两边的高度差h ,可求出两管中的气体的压强差为p B -p A =Θ0gh ,由以上各式,得 v =2Θ0g h �Θ.因此,测量出h 就可以求出气流的速度.41液流和气流的空吸作用如图4所示,若在水平管的细颈外开一小孔A ,用细管接入容器B 中液体内,流动液体不但不会流出,而且容器B 中液体可以被吸上去,为研究此原理,做如下计算:设左上方容器图4E 很大,流体流动时,液面无显著下降,液面与出液孔的高度差为h ,S A 和S F 分别表示水平管上小孔A 与出液孔F 处的横截面积,用Θ表示液体的密度,液体为理想流体,取容器中液面上的点和水平管上小孔以及出液孔F 处的水作为研究对象,根据伯努利方程,有p C +Θg h =p A +12Θv A 2=p F +12Θv F 2,①又因为p C =p F =p 0,代入①式,有v F 2=Θg h ,②p A -p 0=12Θ(v F 2-v A 2),③根据流体在水平管中做稳定流动时,管中各处的流量Q =ΘvS t 不变,有v F v A =S AS F,④由②、③、④式及S F >S A ,得p A -p 0=12Θg h (1-S F 2S A2)<0.⑤即小孔C 处有一定的真空度,因此可将容器B 中液体吸入,这种现象叫做空吸作用,如果容器E 中液面与出水孔处的高度差和S FS A的比值足够大,且在细颈小孔A 处用的细管接在一封闭的容器上,那么,封闭容器里的空气会被逐渐抽出,最后封闭容器内的气压随之减小,即达到抽真空之目的.不但液流有空吸作用,气流也同样有空吸作用,所遵循的规律也相同.空吸作用的应用很广,化学实验室中的水流抽气机、内燃机的汽化器、蒸汽锅加水所用的射水器都是根据这个原理制成的.51日常生活中的实例飞机能够飞上蓝天,是因飞机机翼上方空气流速大于下方,产生向上的压强差,从而获得向上的压力.河里航行的船只总是被迫向水流较急的一面靠拢,是因当水的流速较大一面压强较小,流速小的一面压强较大,船体受到指向流速较大的一面的水的压力.疾速的汽车在公路上行驶时,路旁的纸屑常吸向汽车,是因高速运动的汽车带动周围的空气运动,在其后尾部形成一低气压区,与周边的空气存在压强差,故路旁的纸屑被迫吸向汽车.高速公路上同向行驶的汽车,河流中并排同向行驶速度较大的船只,均有相互碰撞的危险.究其原因,均可用伯努利方程来解释(收稿日期)E C A .:2000-02-2822。

，伯努利方程及其应用伯努利，1738，瑞士。

动能与压强势能相互转换。

沿流线的伯努利方程将牛顿第二定律应用于控制体内的流体元，沿流线切线方向整理后因为将流体元的加速度转换成欧拉形式的加速度，沿流线的质点导数为则导出得：沿流线积分对于不可压定常流动，则可简化为（3皮托（简称皮托管，为纪念法国人皮托1.5 mm mm）在距前端适B点），在孔后足够长距离处两管弯090成柄状．测速时管轴线沿来流方向放置．设正前方的流速保持为v，静压强为p，流体密度为ρ。

粗细两管中的压强被引入Ｕ形测压计中，Ｕ形管中液体密度ρ。

试求用Ｕ形管液位差h∆m表示流速v的关系式。

解：设流动符合不可压缩无粘性流体定常流动条件。

从皮托管正前方Ａ点到端点Ｏ再到侧壁孔Ｂ点的ＡＯＢ线是一条流线，Ａ点的速度和压强分别为v 和p ，沿流线ＡＯ段按（Ｂ４．３．４）式列伯努利方程A gz v+22+ρρ022p gz pv++=得0p 因v v B =k 解：= ⎝⎛22g 沿流线法向方向的速度压强关系式由牛顿第二定律：得考虑到几何关系，有 整理，得忽略重力，得若密度为常数，则有 RvnA A A n p p A p n A g 2( cos δρδρδδδθδδρ-==∂∂+-+此式为沿流线法向方向的伯努利方程，应用条件为（1）无粘性流体，（2）不可压流体（3）定常流（4）沿流线法向。

如果流线位直线时，曲率半径为无限大，则 此式与静压力公式相同。

沿总流的伯努利方程hg z z g h g m∆-=--∆=)1( )( m34ρρρ应用连续性方程伯努利方程的意义不可压缩粘性流体内流管道入口流动示意图，设管直径为d,管口外均流速度为U 。

从开始，流体在壁面上被滞止，形成边界层。

边界层外仍保持为均流，称为核心流。

由壁面不滑移条件引起壁面附近的流速降低，为满足质量守恒定律，核心流流速增大，速度廓线由平坦逐渐变为凸出。

随着边界层厚度不断增长，核心流不断加速，直至处四周的边界层相遇，核心流消失，整个管腔被边界层流动充满，此后速度廓线不再变化。

伯努利方程及其应用伯努利方程及其应用一、伯努利简介1.生平简介：伯努利，d．(danielbernoulli1700～1782)瑞士物理学家、数学家、医学家。

1700年2月8日生于荷兰格罗宁根。

著名的伯努利家族中最杰出的一位。

他是数学家j．伯努利的次子，和他的父辈一样，违背家长要他经商的愿望，坚持学医，他曾在海得尔贝格、斯脱思堡和巴塞尔等大学学习哲学、论理学、医学。

1721年取得医学硕士学位。

努利在25岁时(1725)就应聘为圣彼得堡科学院的数学院士。

8年后回到瑞士的巴塞尔，先任解剖学教授，后任动力学教授，1750年成为物理学教授。

在1725～1749年间，伯努利曾十次荣获法国科学院的年度奖。

1782年3月17日，伯努利在瑞士巴塞尔逝世，终年82岁。

2.成就简介：(1)在物理学方面：①1938年出版发行了《流体动力学》一书，共13章。

这就是他最重要的著作。

书中用能量守恒定律化解流体的流动问题，写下了流体动力学的基本方程，后人称作“伯努利方程”，明确提出了“流速减少、应力减少”的伯努利原理。

②他还提出把气压看成气体分子对容器壁表面撞击而生的效应，建立了分子运动理论和热学的基本概念，并指出了压强和分子运动随温度增高而加强的事实。

③从1728年起至，他和欧拉还共同研究触感而存有弹性的链和梁的力学问题，包含这些物体的均衡曲线，还研究了弦和空气柱的振动。

④他曾因天文测量、地球引力、潮汐、磁学、洋流、船体航行的平衡、土星和木星的圆形运动和振动理论等成果而得奖。

（2）在数学方面：有关微积分、微分方程和概率论等，他也做了大量而重要的工作二、伯努利方程1.定义：充分反映理想流体运动中速度、应力等参数之间关系的方程式。

伯努利方程就是理想流体定常流动的动力学方程，意为流体在忽略粘性损失的流动中，流线上任意两点的压力势能、动能与位势能之和保持不变。

2.伯努利方程概述：理想单轴流体在有势体积力促进作用UX21LI2677E定常运动时，运动方程沿流线分数而获得的抒发运动流体机械能动量的方程。

伯努利方程及其应用摘要:伯努利方程是为了反应理想流体运动中速度、压强等参数之间关系的方程式，伯努利方程揭示流体在重力场中流动时的能量守恒。

并应用伯努利方程解释其在生活中的应用，例如飞机机翼问题，喷油器的质量流量问题等。

经过了一个学期的物理学习，我们学习了关于物理的试验方法与结论，而我对流体力学的伯努利方程十分感兴趣，进一步了解了一些实际生活中的应用。

关键词:伯努利方程，理想流体力学，机械能守恒，生活中的应用。

参考文献:百度百科，大学物理教程。

伯努利开辟并命名了流体动力学这一学科，区分了流体静力学与动力学的不同概念。

1738年，他发表了十年寒窗写成的《流体动力学》一书。

他用流体的压强、密度和流速等作为描写流体运动的基本概念，引入了“势函数”“势能”(“位势提高”)来代替单纯用“活力’讨论，从而表述了关于理想流体稳定流动的伯努利方程，这实质上是机械能守恒定律的另一形式。

他还用分子与器壁的碰撞来解释气体压强，并指出，只要温度不变，气体的压强总与密度成正，与体积成反比，用此解释了玻意耳定律。

伯努利方程是理想流体定常流动的动力学方程，意为流体在忽略粘性损失的流动中，流线上任意两点的压力势能、动能与位势能之和保持不变。

伯努利方程揭示流体在重力场中流动时的能量守恒。

理想正压流体在有势体积力作用下作定常运动时，运动方程(即欧拉方程)沿流线积分而得到的表达运动流体机械能守恒的方程。

因著名的瑞士科学家D.伯努利于1738年提出而得名。

对于重力场中的不可压缩均质流体，方程为p+ρgh+(1/2)*ρv^2=c 式中p、ρ、v分别为流体的压强、密度和速度;h为铅垂高度;g为重力加速度;c为常量。

上式各项分别表示单位体积流体的压力能 p、重力势能ρgh和动能(1/2)*ρv ^2，在沿流线运动过程中，总和保持不变，即总能量守恒。

但各流线之间总能量(即上式中的常量值)可能不同。

对于气体，可忽略重力，方程简化为p+(1/2)*ρv ^2,常量(p0)，各项分别称为静压、动压和总压。

伯努利方程的应用伯努利方程对于流动体系除了掌握体系的对于流动体系，除了掌握体系的物料衡算关系以外，还必须找出体系各种形式能量之间的转换关系系各种形式能量之间的转换关系。

伯努利(Bernoulli)方程：描述了流体流动过程中各种形式能量之间的转换关系，是流体在定常流动情。

是热力学第一Daniel Bernoulli ，1700-1782况下的能量衡算式是热力学第定律对流体流动过程的具体描述。

流动系统的能量流动系统的能量：流动系统的能量流动系统的能量：(3) 动能：流体以一定的速度运动时便具有一定的动能，大时所需要的功小等于流体从静止加速到流速v时所需要的功。

(4) 静压能：流体进入划定体积时需要对抗压力所做的功。

流体进入划定体积时需要对抗压力所做的功若质量为m的流体体积为，某截面处的静压强为p，截面面积为A，则将质量为m的流体压入划定体积的功为：则将质量为的流体压入划定体积的功为质量为能量还可以通过其他外界条件与流动系统进行交换，包括：：流体通过换热器吸热或放热Q e吸热时为正，放热时为负。

：泵等流体输送机械向系统做功W em 的流体交换热量=m Q e流体接受外功为正流体对外作功为负作功为负的流体所接受的功= mW e以截面两边同除以m单位质量流体稳定流动过程的总能量衡算式，流动系统的力学第一定律表达式系统内能变化系统内能变化：是单位质量流体从截面1-1到截面是单位质量流体从截面1-1到截面2-2流体通过环境直接获得的热量，Q e(1)流体通过环境直接获得的热量流体流动时需克服阻力做功，因而消耗机械能转化为热量，若流体等温流动，这部分热量则散失到系统外部。

设单位流体因克服阻力而损失的，则则不可压缩流体ρ=const=0无外加功W e=0理想流体，Σhf伯努力方程努力方程的有关伯努力方程的讨论(1)伯努力方程的适用条件：不可压缩的理想流体做定常流动而无外功输入的情况，选取截面符合缓变流条件。

单位质量流体在任一截面上所具有的势能、动能和静压能之和是一常数。

伯努利方程原理及其应用伯努利方程原理是流体力学中的一个重要定理，描述了流体在不同位置的压力、速度和高度之间的关系。

它是基于质量守恒和动量守恒定律得出的。

伯努利方程的应用非常广泛，涉及许多领域，如水力工程、航空航天工程、血液循环等。

P + 1/2ρv² + ρgh = 可以称之为 Bernoulli's Principle 分成三个代表量就是 (pressure), (velocity) and (height)其中，P代表流体的压力，ρ代表流体的密度，v代表流体的流速，g代表重力加速度，h代表流体的高度。

这个方程的意义是，当流体在稳定非粘性的情况下沿着流线流动时，流体在不同位置上的压力、速度和高度之间是相互关联的。

1.水力工程：伯努利方程可以用来研究液体在管道流动中的压力和速度变化。

在水力工程中，通过伯努利方程可以计算水管中的液体流速、压力等参数，从而确定水力机械设备的设计和运行参数。

2.航空航天工程：伯努利方程可以用来研究气体在飞行器周围的流动。

当气体流动速度增加时，伯努利方程能够说明气体的压力减小。

这一原理被应用在飞机的翼型设计中，通过加速飞行器周围的气流，可以产生升力，从而使飞机升起。

3.血液循环：伯努利方程可以用来研究血液在血管中的流动。

血液在动脉和静脉中的流速和压力变化可以通过伯努利方程来描述。

在生理学中，伯努利方程被用来分析血管疾病的发生机制，如动脉瘤、血栓形成等。

4.分离气体传输：伯努利方程在管道气体输送过程中也有重要应用。

通过伯努利方程可以计算气体在管道中的流速和压力变化，从而确定管道的设计和运行参数。

此外，伯努利方程还可以应用于喷射器、超声波仪器、气象学中的风场分析等领域。

总的来说，伯努利方程通过描述流体在不同位置的压力、速度和高度之间的关系，为流体力学的研究和应用提供了基础。

通过对伯努利方程进行分析和应用，可以更好地理解和预测流体力学现象的发生和发展。

伯努利方程的应用概述伯努利方程是流体力学中十分重要的方程之一，它描述了在不可压缩和不黏滞的流体中，沿着流线，流速增加时压力减小的现象。

这个方程被广泛应用于各种领域，包括流体力学、空气动力学、水力学、航空航天工程等。

本文将对伯努利方程的应用进行概述。

一、流体力学中的应用：1.流体力学实验：伯努利方程可以用来解释在流体力学实验中观察到的现象。

例如，在喷气装置中，当液体从小孔中喷射出来时，其速度增加，压力减小，这可以通过伯努利方程解释。

2.水力学：伯努利方程在研究液体流动、水流以及水力工程中具有广泛的应用。

例如，在水力发电站中，伯努利方程可以用来计算水流速度、水压力以及能量转换等。

3.管道流动：在管道中的流体流动中，伯努利方程可以用来分析不同位置的压力变化。

例如，在一个升压站或者消防设备中，伯努利方程可以用来计算流体的流速、压力以及流量等。

4.飞行器的气动性能：伯努利方程在航空航天工程中的应用是非常重要的。

例如，它可以用来计算飞机机翼产生的升力以及飞机的飞行性能。

二、空气动力学中的应用：1.喷气发动机：伯努利方程在喷气发动机中的应用是十分重要的。

当高速气流通过喷射嘴时，嘴内速度增加，压力降低，通过伯努利方程可以计算出发动机喷气的动力和效率。

2.空气动力学实验：伯努利方程也可以用来解释空气动力学实验中的现象。

例如，在风洞实验中，通过空气通过不同形状的模型，可以通过伯努利方程计算流体的流速、压力以及飞机的气动性能。

三、航空航天工程中的应用：1.飞行器气动性能分析：伯努利方程可以用来分析飞行器在不同飞行状态下的气动性能，例如飞机的升力、阻力等。

通过伯努利方程，可以对飞行器的设计和改进提供重要的参数和数据支持。

2.火箭发动机推力计算：伯努利方程在火箭发动机的设计和性能分析中也具有重要的应用。

通过伯努利方程，可以计算火箭喷射气流的速度、压力以及推力等。

综上所述，伯努利方程在流体力学、空气动力学以及航空航天工程中的应用是广泛而重要的。

伯努利方程的应用学号：PB05000606 姓名：赵志飞在我们学习流体力学是我们提到一个非常重要的方程，他就是伯努利方程。

伯努利方程在许多方面有着非常广泛的应用，现在我们就其中的某些方面做一些粗浅的介绍。

伯努利方程常量=++p gz v ρρ221 左式称为伯努利方程，由瑞士科学家伯努利（D.Bernoulli,1700-1782）于1738年首先导出。

它实际上是流体运动中的功能关系式，即单位体积流体的机械能的增量等于压力差所做的功。

必须指出，伯努利方程右边的常量，对于不同的流管，其值不一定相同。

相关应用（1） 等高流管中流速与压强的关系根据伯努利方程在水平流管中有常量=+p v 221ρ 故流速v 大的地方压强p 小，反之，流速小的地方压强大。

在粗细不均匀的水平流管中，根据连续性方程，管细处流速大，管粗处流速小，所以管细处压强小，管粗处压强大。

从动力学角度分析，当流体沿水平管道运动时，其质元从管粗处流向管细处将加速，使质元加速的作用力来源于压强差。

水流抽气机和喷雾器就是基于这一原理制成的。

下面是一些实例：水翼艇水翼艇是一种在艇体装有水翼的高速舰艇．在通常情况下水翼艇能以93千米／小时的速度持续航行，最高航速可达110千米／小时．水翼艇之所以速度么快，关键是能在水上飞行．它的飞行，全靠它那副特有的水翼．水翼的上下表面水流速不同，这就在水翼的表面造成了上下的压强差，于是在水翼上就产生了一个向上的举力．当水翼艇开足马力到达一定的速度时，水翼产生的举力开始大于艇体的重力，把艇体托出水面，使艇体与水面保持一定的距离，减小了舰艇在水中的航行阻力．水流抽气机典型的水流抽气机的外观．它的上端较粗的口径处和水龙头的出水口相接．其直下方的开口则为水流出口．在它的侧方的连通管则连接到欲抽气的容器上．当使用时，则为如下图的情形．水流抽气机和水龙头以橡皮管连接，相接处皆以管束栓紧．（下图是管束图片）右侧的连通管亦以管束栓紧橡皮管后再连接到吸滤瓶上．当水管中的水向下流出进入水流抽气机时，因水流抽气机的内部有导流的构造，可使水流经由一较小的通道冲下，造成水流加速的效应．当水的流速加快时，在其近旁的空气分子的运动速率也会加快；由伯努利原理可知：在其侧管内靠近水流的气体压力应较其外侧的气体压力低．因此使得侧管的气体不断地向水流处移动，而产生了抽取其它容器中气体的功能．例：在稳定的流体系统中，谁连续从粗管流入细管。