伯努利方程式

伯努利方程三种形式公式
第一种形式的伯努利方程公式是：
P₁ + 1/2ρv₁² + ρgh₁ = P₂ + 1/2ρv₂² + ρgh₂
其中P₁和P₂分别表示两个位置的压力，ρ表示流体的密度，v₁和v₂表示两个位置的流速，g为重力加速度，h₁和h₂表示两个位置的高度。

这个公式描述了流体在两个位置之间能量守恒的关系。

等式左边的第
一项表示压力能，第二项表示动能，第三项表示单位质量的重力势能。

等
式右边的三项表示相应位置的压力能、动能和重力势能。

这个公式适用于
流体在不完全关闭的管道、管道两端处于同一高度的情况。

第二种形式的伯努利方程公式是：
P + 1/2ρv² + ρgh = const
这是一个简化形式的伯努利方程，它将两个位置的参数合并成一个常数。

这个公式的物理意义是，当流体在流动过程中没有受到外界力的作用时，流体的总能量保持不变。

这个公式适用于理想的水平管道、无摩擦的
流动。

第三种形式的伯努利方程公式是：
P + 1/2ρv² = const
这是伯努利方程的最简形式，它忽略了重力势能的影响。

这个公式适
用于理想的非粘性流体在无重力情况下的流动，如气体等。

这三种形式的伯努利方程公式分别适用于不同的流体力学问题。

选择
适用的公式取决于具体的流动条件和需要分析的问题。

无论选择哪种形式，
伯努利方程都提供了一个重要的工具，可以帮助我们研究流体力学中的能量转换和守恒。

伯努利定律在一个流体系统，比如气流、水流中，流速越快，流体产生的压力就越小，这就是被称为“流体力学之父”的丹尼尔·伯努利1738年发现的“伯努利定律”。

这个压力产生的力量是巨大的，空气能够托起沉重的飞机，就是利用了伯努利定律。

飞机机翼的上表面是流畅的曲面，下表面则是平面。

这样，机翼上表面的气流速度就大于下表面的气流速度，所以机翼下方气流产生的压力就大于上方气流的压力，飞机就被这巨大的压力差“托住”了。

当然了，这个压力到底有多大，一个高深的流体力学公式“伯努利方程”会去计算它。

方程式v=流动速度伯努利定律g=地心加速度(地球)h=流体处于的高度(从某参考点计)p=流体所受的压强ρ=流体的密度伯努利方程伯努利理想正压流体在有势彻体力作用下作定常运动时，运动方程（即欧拉方程）沿流线积分而得到的表达运动流体机械能守恒的方程。

因著名的瑞士科学家D.伯努利于1738年提出而得名。

对于重力场中的不可压缩均质流体，方程为p+ρgz+(1/2)*ρv^2=C式中p、ρ、v分别为流体的压强、密度和速度；z 为铅垂高度；g为重力加速度。

上式各项分别表示单位体积流体的压力能p、重力势能ρg z和动能(1/2)*ρv ^2，在沿流线运动过程中，总和保持不变，即总能量守恒。

但各流线之间总能量（即上式中的常量值）可能不同。

对于气体，可忽略重力，方程简化为p+(1/2)*ρv ^2=常量(p0)，各项分别称为静压、动压和总压。

显然，流动中速度增大，压强就减小；速度减小，压强就增大；速度降为零，压强就达到最大(理论上应等于总压)。

飞机机翼产生举力，就在于下翼面速度低而压强大，上翼面速度高而压强小，因而合力向上。

据此方程，测量流体的总压、静压即可求得速度，成为皮托管测速的原理。

在无旋流动中，也可利用无旋条件积分欧拉方程而得到相同的结果但涵义不同，此时公式中的常量在全流场不变，表示各流线上流体有相同的总能量，方程适用于全流场任意两点之间。

第四章 伯努利方程4.1 伯努利方程4.1.1 理想流体沿流线的伯努利方程1. 伯努利方程的推导将欧拉运动微分方程式积分可以得到流体的压力分布规律，但只能在特殊的条件下，不可能在任何的情况下都可求得其解，故我们需对流场作出如下假设：（1）理想流体（2）定常流动（3）质量力有势（4）不可压缩流体（5）沿流线积分在定常流动的条件下，理想流体的运动微分方程（欧拉运动微分方程）可以写成 ⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂+∂∂+∂∂=∂∂-∂∂+∂∂+∂∂=∂∂-∂∂+∂∂+∂∂=∂∂-z v v y v v x v v z p f z v v y v v x v v y p f z v v y v v x v v x p f z z z y z x z y z y y y x y x z x y x x x ρρρ111 (4.1) 将这个方程沿流线积分，如图4.1所示，可得到伯努利方程。

为此，将式(4.1)的第一式乘以x d 得x zv v x y v v x x v v x x p x f x z x y x x x d d d d 1d ∂∂+∂∂+∂∂=∂∂-ρ （1） 按照流线方程 zy x v z v y v x d d d == 将有，y v x v x y d d =，z v x v x z d d =故式（1）可写成x x x x x x x x x v v z zv v y y v v x x v v x x p x f d d d d d 1d =∂∂+∂∂+∂∂=∂∂-ρ （2） 式(4.1)的另外两式分别乘y d 、z d 后，作类似的代换，可得y y y v v y yp y f d d 1d =∂∂-ρ （3）z z z v v z zp z f d d 1d =∂∂-ρ （4） 将式（2）、（3）和式（4）相加，得 z z y y x x z y x v v v v v v z zp y y p x x p z f y f x f d d d )d d d (1d d d ++=∂∂+∂∂+∂∂-++ρ （5） p 的全微分可以表示为 dz zp dy y p dx x p dp ∂∂+∂∂+∂∂= 质量力有势，则必存在势函数U ，满足y f y f x f z zU y y U x x U U y y x d d d d d d d ++=∂∂+∂∂+∂∂=而 2/d d d d 2v v v v v v v z z y y x x =++式中等号右端的v 为平均速度。

伯努利原理公式伯努利原理往往被表述为p+1/2ρv2+ρgh=C，这个式子被称为伯努利方程。

式中p为流体中某点的压强，v为流体该点的流速，ρ为流体密度，g为重力加速度，h为该点所在高度，C是一个常量。

它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。

伯努利方程是丹尼尔•伯努利在 1726 年研究理想液体作稳定流动时提出的。

静压是流体真实存在的压强值，动压也称为速压或速度头，其单位也是Pa。

动压起到调节静压在总压中所占比例的作用：动压越大，静压越小；动压越小，静压越大；动压为零时，即流速为零，静压最大且等于总压值。

因此，伯努利方程式的物理含义也可以说成是流体的压强能和动能之间可以相互转化，但流动的总机械能保持不变。

伯努利方程是流体力学的基本方程，它反映了理想液体作稳定流动时，压强、流速和高度三者之间的关系。

答案】一、一般条件下伯努利方程在各项的意义P +1/2ρv2 +ρgh = 常量该方程说明理想流体在流管中作稳定流动时,单位体积的动能1/2ρv2 、重力势能ρgh 、该点的压强P 之和为一个常量.其中1/2ρv2相与流速有关,常称为动压,ρgh 和P 相与流速无关,常称为静压.二、单位重量流体中伯努利方程各项的物理意义ρg =m/u g =mg/u表示单位体积的重力,以ρg 除各项得:p/ρg+v平方/2 g+ h = 常量该方程表示流场中一点上单位重量流体所具有的总机械能. 其中p/ρg表示流场中一点上单位重量流体所具有的压力潜能,也就是压力对单位体积重量流体所做的功,v平方/2 g 表示单位重量流体所具有的动能, h 就是流场中该点的高度.由于v平方/2 g+ p/ρg+ z = 常数,定理中每一项都具有长度的量纲. 所以p/ρg 表示所考察点的压力潜能的同时也可表示它能将流体压升到某一高度的能力.三、单位质量流体中伯努利方程p/ρ项的物理意义以ρ除各项得:p/ρ+1/2 v平方 + gh = 常量该方程中:p/ρ项表示流场中某一点上单位质量流体所具有的压力或弹性势能,从能量的角度讨论p/ρ项也可理解为单位质量流体相对于p = 0 状态所蕴涵的能量.综上所述：通过以上的分析推导可以看出伯努利方程是能量方程式,尽管分析问题所用的动力学原理不同,但导出方程的意义是完全相同的,说明在管内作稳定流动的理想液体具有压力能、势能和动能三种形式的能量,在适合限定条件的情况下,流场中的三种能量都可以相互转换,但其总和却保持不变,这三种能量统称为机械能. 由此可以得出:伯努利方程在本质上是机械能的转换与守恒.。

伯努利原理公式推导
伯努利原理是描述流体力学中流体运动的基本原理之一。

它表明在光滑的管道中，流体在速度增加的地方压力会降低，而在速度减小的地方压力会增加。

下面是伯努利原理的公式推导过程：
考虑一个流体在管道中的某一点A和另一点B，流体通过这两个点的截面积分别为A和B，流体的速度为vA和vB，压强为pA和pB。

我们假设流体是不可压缩的，即流体的密度是恒定的。

根据质量守恒定律，单位时间内通过截面A的流体质量等于通过截面B的流体质量，即ρAvA = ρBvB，其中ρ是流体的密度。

根据动量守恒定律，单位时间内通过截面A的动量变化等于通过截面B的动量变化。

流体的动量可以用动量的定义来表示，即动量 = 质量× 速度。

因此，单位时间内通过截面A的动量变化为ρAvA × vA，通过截面B的动量变化为ρBvB × vB。

根据动量守恒定律，我们可以得到以下方程：
ρAvA × vA = ρBvB × vB
将质量守恒定律的方程式ρAvA = ρBvB代入上述方程，可以
得到：
vA^2 = vB^2 + (pB - pA) / ρ
这就是伯努利原理的公式推导过程。

该公式表明流体在两个点
之间的速度平方与压强差和密度的乘积成反比。

如果速度增加，压
强会降低；如果速度减小，压强会增加。

需要注意的是，伯努利原理的推导是建立在一些假设条件下的，例如流体是不可压缩的、流体是理想流体、流体是稳定的等。

在实
际应用中，这些假设条件可能不完全成立，因此在具体问题中需要
综合考虑其他因素。

伯努利方程式
伯努利方程式是一种用来描述随机事件发生概率的数学方程式。

它是在1812年由英国数学家艾伦伯努利发明的，因此得名。

伯努利
方程式的数学表达式是：P(A)=p,P(B)=1-p，其中P(A)和P(B)是A、B事件发生的概率，p∈(0,1)。

这句话的意思是说，A、B两个事件发生的概率为p和1-p。

伯努利方程式具有广泛的应用，它可以用来描述各种随机事件的发生概率，如计算骰子抛掷的概率，解决赌博概率等问题，波兰数学家斯瓦布拉夫斯基有一本著作：《论博弈的数学理论》，就是用伯努利方程式解决赌博概率问题的重要参考书。

伯努利方程式广泛应用于统计学，统计学家和经济学家普遍使用伯努利方程式来解决实际问题。

例如，在市场营销中，伯努利方程式可以用来估计一个新产品成功的概率，以及在竞争中胜出的概率等等。

伯努利方程式还被广泛地应用在生物学上，它在基因遗传学上具有重要的作用。

在单基因遗传模型中，伯努利方程式可以用来估算父母亲的两个遗传物质合并的结果，从而预测子代的数量和性状特征。

通过以上介绍，不难看出，伯努利方程式在不同领域有着广泛的应用，它是一种十分重要的数学方程式。

因此，在理解伯努利方程式之前，我们需要了解数学概念，如概率和概率分布等。

除此以外，我们还应该掌握伯努利方程式解决具体问题的方法，以便在实际应用中更好地灵活运用。

- 1 -。

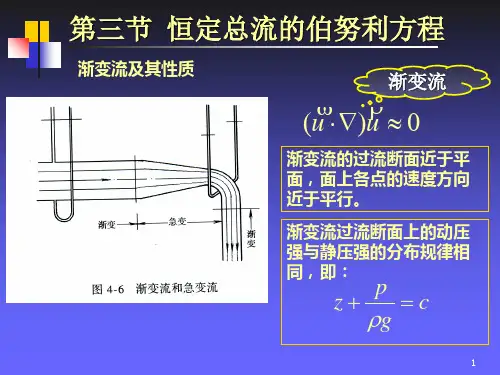
，伯努利方程及其应用伯努利，1738,瑞士。

动能与压强势能相互转换。

沿流线的伯努利方程将牛顿第二定律应用于控制体内的流体元，沿流线切线方向(dp、dS y-pgdA8scos0 + pdA- p + dA = p3\dsdv(a.t)dt整理后八 1 dp dv(a,t)-geos 0 ---------- =p dsdt因为COS0 =—ds将流体元的加速度转换成欧拉形式的加速度，沿流线的质点导数为dv{a,t) _ Dv(s.t) _ dv dt Dt dt 则导出dz 1 dp dv dv —g -- -------- = — + v —ds p dsdtds此式为一维欧拉方程，使用下述关系将方程沿流线积分。

两边乘以ds— ds 二dz. — ds = dp2 = dv dsds ds得：dv 1 , 7 1 7 —ds + vdv + gdz -\— dp — 0 dt p沿流线积分0ds + l + g 卄淫二常数 J dt 2 p此式为欧拉方程的积分式，适合于可压、无粘不定常运动。

对于不可压定常流动，则可简化为2— + gz + —二常数 2 P此式为伯努利方程，三项分别表示单位质量流体具有dv+ v — ds的动能、位置势能和压强势能。

即总机械能守恒。

应用伯努利方程时常采用沿流线上任两点的总机械能值相等的形式。

伯努利方程使用的限制条件（1）无粘性流体，（2） 不可压流体（3）定常流（4）沿流线。

加入能量损失就可适应粘性流体。

皮托（pitot ）测速管：总压强与动压强皮托测速管又称为皮托-静压管，简称皮托管，为纪 念法国人皮托命名。

皮托测速管由粗细两根同轴的圆 管组成，细管（直径约为1・5 mm ）前端开孔（0点）,粗管（直径约为6 mm ）在距前端适当长距离处的侧壁 上开数个小孔（B 点），在孔后足够长距离处两管弯90。

成柄状.测速时管轴线沿来流方向放置.设正前方的 流速保持为…静压强为八 流体密度为°。