当前位置：文档之家 › 运筹学基础与应用第四版胡运权主编课后练习答案

运筹学基础与应用第四版胡运权主编课后练习答案

  • 格式：doc
  • 大小：1.69 MB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

运筹学(胡运权第四版及答案)

运筹学(胡运权第四版及答案)
管理运筹学
主讲：谢先达
2014.09
联系方式 办公室：QL643 87313663 手机： 13600512360 邮箱： xxdhz@
绪
论
绪论
什么是运筹学？
运筹学发展历史 运筹学主要内容 运筹学的基本特征与基本方法
绪论
什么是运筹学？
定义：为决策机构在对其控制下业务活动进行决策 时，提供以数量化为基础的科学方法。
概念：可行解、最优解、最优值
第一章：线性规划及单纯形法
练习：靠近某河流有两个化工厂，流经第一化工厂的河流流量为每天 500万m3，在两个工厂之间有一条流量为每天200万m3支流，第一化工厂每 天排放含有某种有害物质的工业污水2万m3 ，第二化工厂每天排放这种 工业污水1.4万m3 。从第一化工厂排出的工业污水流到第二化工厂以前， 有20%可自净化。根据环保要求，河流中工业污水的含量应不大于0.2%， 这两个工厂都需各自处理一部分工业污水，第一化工厂处理工业污水的 成本是1000元/万m3 。第二化工厂处理污水的的成本是800元/万m3 。现 问在满足环保要求的条件下，每厂各应处理多少工业污水，使这两个工 厂总的处理工业污水费用最小。
-x1+x2+x3 = 4
-2x1+x2-x3 ≤ 6 x1 ≤ 0,x2 ≥ 0, x3取值无约束
第一章：线性规划及单纯形法
线性规划问题及其数学模型 线性规划图解法
单纯形法原理
单纯形法计算步骤
单纯形法的进一步讨论
第一章：线性规划及单纯形法
x2
目标函数： 约束条件： maxz=50x1+100x2 x1+x2≤300 2x1+x2≤400 x2≤250 x1≥0 ，x2≥0

第四版运筹学部分课后习题解答

第四版运筹学部分课后习题解答

运筹学部分课后习题解答P47 1.1 用图解法求解线性规划问题a）12121212min z=23466 ..424,0x xx xs t x xx x++≥⎧⎪+≥⎨⎪≥⎩解：由图1可知，该问题的可行域为凸集MABCN，且可知线段BA上的点都为最优解，即该问题有无穷多最优解，这时的最优值为min 3z=23032⨯+⨯=P47 1.3 用图解法和单纯形法求解线性规划问题a）12121212max z=10x5x349 ..528,0x xs t x xx x++≤⎧⎪+≤⎨⎪≥⎩解：由图1可知，该问题的可行域为凸集OABCO，且可知B点为最优值点，即112122134935282xx xx x x=⎧+=⎧⎪⇒⎨⎨+==⎩⎪⎩，即最优解为*31,2Tx⎛⎫= ⎪⎝⎭这时的最优值为max335z=101522⨯+⨯=单纯形法： 原问题化成标准型为121231241234max z=10x 5x 349..528,,,0x x x s t x x x x x x x +++=⎧⎪++=⎨⎪≥⎩ j c →105B CB Xb 1x2x3x4x0 3x 9 3 4 1 0 04x8[5] 2 0 1 j j C Z -105 0 0 0 3x 21/5 0 [14/5] 1 -3/5 101x8/51 2/5 0 1/5 j j C Z -1 0 -2 5 2x 3/2 0 1 5/14 -3/14 101x11 0 -1/72/7j j C Z --5/14 -25/14所以有*max 33351,,1015222Tx z ⎛⎫==⨯+⨯= ⎪⎝⎭P78 2.4 已知线性规划问题：1234124122341231234max24382669,,,0z x x x x x x x x x x x x x x x x x x x =+++++≤⎧⎪+≤⎪⎪++≤⎨⎪++≤⎪≥⎪⎩求: (1) 写出其对偶问题；（2）已知原问题最优解为)0,4,2,2(*=X ，试根据对偶理论，直接求出对偶问题的最优解。

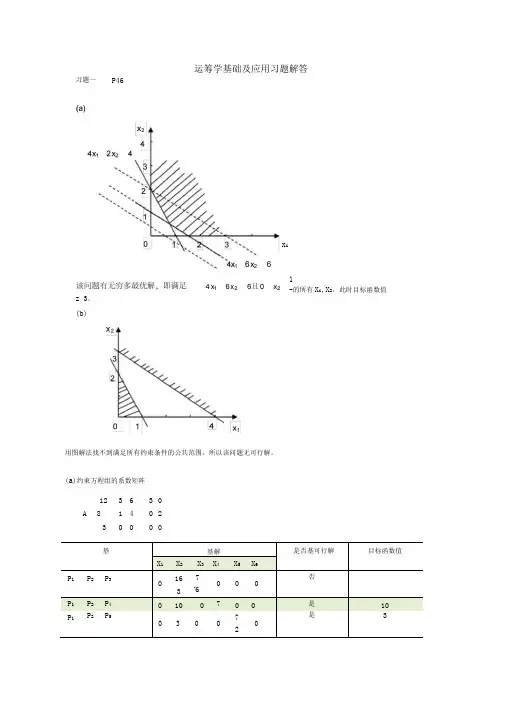
运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用习题解答z 3。

(b)用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解。

(a)约束方程组的系数矩阵12 3 6 3 0A 8 1 4 0 23 0 0 0 0基基解是否基可行解目标函数值X1 X2 X3 X4 X5 X6P1 P2 P3163 7-60 0 0否P1 P2 P4 0 10 0 7 0 0 是10P1 P2 P50 3 0 0 72是 3习题一P46x i1-的所有X i,X2，此时目标函数值o(b)约束方程组的系数矩阵A 12 3 4A2 2 12⑻(1)图解法基 基解 是否基可行解 目标函数值X 1X 2X 3X 4P 1P 24 11否"2P 1P 3 2 0 110 是435 ~5~5P 1P 4111否—36P 2P 312是52P 2P 41否22P 3P 40 0 1 1是5最优解xT2 11 5吋omax z 10x 1 5x 2 0x 3 0x 4 3x i 4X 2 X 3st. 5x 1 2x 2 x 48 9 8 12。

min—,— — 5 3 5C j 105 0 0 C B基b X 1X 2X 3X 421143 0 X 3— 1—"5"5582110X 11C j 105 0 0 C B 基bX 1 X 2 X 3 X 4 0 X 3 9 341 0 0X 48[5] 20 1 C j Z j105令 X iX 20,0,9,8，由此列出初始单纯形表最优解即为3x1 4x2 9的解x5x 1 2x 2 81,-，最大值z 竺 2 2(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式则P 3，P 4组成一个基。

得基可行解xC j Z j0 1221 8320，min14 22新的单纯形表为C j 105 0 0 C B基b X 1X 2X 3X 435 3 5X 2— 01— —2141410X 11121—7525c jZ j14 143*35x i 1, x 2 - , X 3 0, X 4 0。

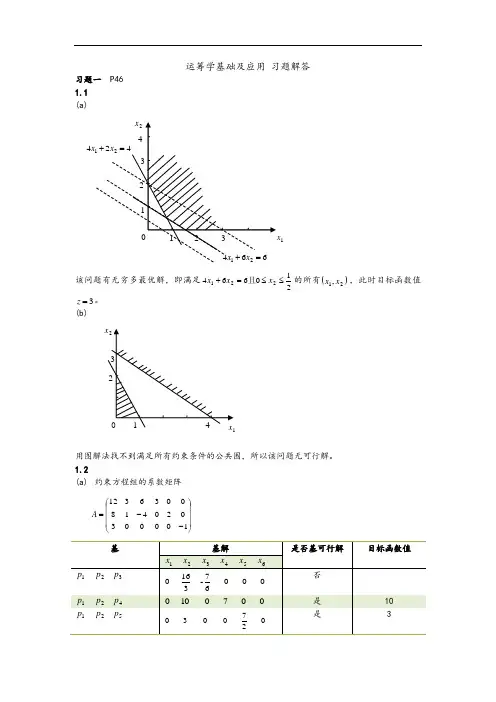
运筹学基础及指导应用第四版胡运权主编课后练习问题详解

运筹学基础及指导应用第四版胡运权主编课后练习问题详解

运筹学基础及应用 习题解答习题一 P46 1.1 (a)该问题有无穷多最优解，即满足210664221≤≤=+x x x 且的所有()21,x x ，此时目标函数值3=z 。

(b)用图解法找不到满足所有约束条件的公共围，所以该问题无可行解。

1.2(a) 约束方程组的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛--=1000030204180036312A4最优解()T x 0,0,7,0,10,0=。

(b) 约束方程组的系数矩阵⎪⎪⎭⎫⎝⎛=21224321A最优解Tx ⎪⎭⎫⎝⎛=0,511,0,52。

1.3(a)(1) 图解法最优解即为⎩⎨⎧=+=+8259432121x x x x 的解⎪⎭⎫⎝⎛=23,1x ，最大值235=z(2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 ⎩⎨⎧=++=+++++=825943 ..00510 max 4213214321x x x x x x t s x x x x z则43,P P 组成一个基。

令021==x x得基可行解()8,9,0,0=x ，由此列出初始单纯形表 21σσ>。

5839,58min =⎪⎭⎫ ⎝⎛=θ02>σ，2328,1421min =⎪⎭⎫ ⎝⎛=θ0,21<σσ，表明已找到问题最优解0 , 0 , 231,4321====x x x x 。

最大值 235*=z (b)(1) 图解法最优解即为⎩⎨⎧=+=+524262121x x x x 的解⎪⎭⎫⎝⎛=23,27x ，最大值217=z(2) 单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式1234523124125max 2000515.. 62245z x x x x x x x s t x x x x x x =+++++=⎧⎪++=⎨⎪++=⎩21=+x x 2621+x x则3P ，4P ，5P 组成一个基。

令021==x x得基可行解()0,0,15,24,5x =，由此列出初始单纯形表21σσ>。

第四版运筹学部分课后习题解答(内容参考)

第四版运筹学部分课后习题解答(内容参考)

运筹学部分课后习题解答P47 1.1 用图解法求解线性规划问题a）12121212min z=23466 ..424,0x xx xs t x xx x++≥⎧⎪+≥⎨⎪≥⎩解：由图1可知，该问题的可行域为凸集MABCN，且可知线段BA上的点都为最优解，即该问题有无穷多最优解，这时的最优值为min 3z=23032⨯+⨯=P47 1.3 用图解法和单纯形法求解线性规划问题a）12121212max z=10x5x349 ..528,0x xs t x xx x++≤⎧⎪+≤⎨⎪≥⎩解：由图1可知，该问题的可行域为凸集OABCO，且可知B点为最优值点，即112122134935282xx xx x x=⎧+=⎧⎪⇒⎨⎨+==⎩⎪⎩，即最优解为*31,2Tx⎛⎫= ⎪⎝⎭这时的最优值为max335z=101522⨯+⨯=单纯形法： 原问题化成标准型为121231241234max z=10x 5x 349..528,,,0x x x s t x x x x x x x +++=⎧⎪++=⎨⎪≥⎩ j c →105B CB X b 1x2x3x4x0 3x 9 3 4 1 0 04x8[5] 2 0 1 j j C Z -105 0 0 0 3x 21/5 0 [14/5] 1 -3/5 101x8/51 2/5 0 1/5 j j C Z -1 0 -2 5 2x 3/2 0 1 5/14 -3/14 101x11 0 -1/72/7j j C Z --5/14 -25/14所以有*max 33351,,1015222Tx z ⎛⎫==⨯+⨯= ⎪⎝⎭P78 2.4 已知线性规划问题：1234124122341231234max24382669,,,0z x x x x x x x x x x x x x x x x x x x =+++++≤⎧⎪+≤⎪⎪++≤⎨⎪++≤⎪≥⎪⎩求: (1) 写出其对偶问题；（2）已知原问题最优解为)0,4,2,2(*=X ，试根据对偶理论，直接求出对偶问题的最优解。

清华大学《运筹学教程》胡运权主编课后习题答案

清华大学《运筹学教程》胡运权主编课后习题答案

3 x1 x2 x5 3
st
4 x1 3 x2 x3 x6
x1
2 x2
x4
4
6
x j 0（, j 1,,4）
cj
CB
xB
b
-M x5 3
-M
x6
6
0
x4
4
cj zj
-4 x1 1
-M x6 2
0
x4
3
cj zj
-4
-1 0
x1
x2
x3
3
1
0
4
3 -1
1
20
7M-4 4M-1 -M
小于0 ,因此已经得到唯一最优解，最优解为：
X * 2 5 ,9 / 5,1,0T
max Z 10x1 15x2 12x3
5x1 3x2 x3 9
(4)
st
5x1 2x1
6x2 x2 x3
15x3 5
15
x j 0（, j 1,,3）
39
1.8 已知某线性规划问题的初始单纯形
表和用单纯形法迭代后得到下面表格,试求括
弧中未知数a∼l值。
项目
X1 X2 X3 X4 X5
X4 6 (b) (c) (d) 1 0
X5 1 -1 3 (e) 0 1
Cj－Zj
a -1 2 0 0
X1 (f) (g) 2 -1 1/2 0
X5 4 (h) (i) 1 1/2 1
Cj－Zj
0 -7 (j) (k) (l)
6 4
x1 , x2 0
无穷多最优解
(蓝 色 线 段 上 的 点 都 是 最优 解 ）
x1
6 5
,
x2

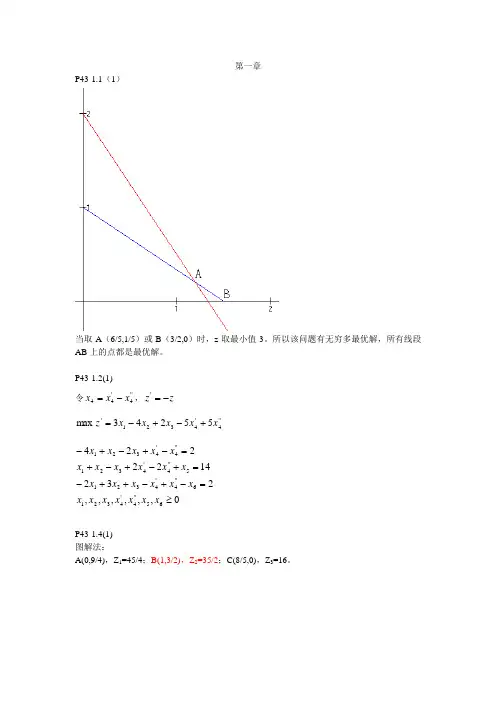
运筹学胡运权 部分课后习题答案

运筹学胡运权 部分课后习题答案

第一章P43-1.1（1）当取A （6/5,1/5）或B （3/2,0）时，z 取最小值3。

所以该问题有无穷多最优解，所有线段AB 上的点都是最优解。

P43-1.2(1)令''4'44x x x -=，z z -='''4'4321'55243max x x x x x z +-+-=,,,,,,232142222465''4'43216''4'43215''4'4321''4'4321≥=-+-++-=+-+-+=-+-+-x x x x x x x x x x x x x x x x x x x x x x x xP43-1.4(1) 图解法：A(0,9/4)，Z 1=45/4；B(1,3/2)，Z 2=35/2；C(8/5,0)，Z 3=16。

单纯形法：10 5 0 0C b X b b x1x2x3x4θ0 x39 3 4 1 0 30 x48 5 2 0 1 8/5δ10 5 0 00 x321/5 0 14/5 1 -3/5 3/210 x18/5 1 2/5 0 1/5 4δ0 1 0 -25 x23/2 0 1 5/14 -3/1410 x1 1 1 0 -1/7 2/7δ0 0 -5/14 -25/14依次相当于：原点；C；B。

P44-1.7(1)2 -1 2 0 0 0 -M -M -MC b X b b x1x2x3x4x5x6x7x8x9θ无界解。

两阶段法：阶段二：P45-1.10证明：CX (0)>=CX*，C*X*>=C*X (0) CX (0)-CX*+C*X*-C*X (0)>=0，即(C*-C)(X*-X (0))>=0。

P45-1.13设饲料i 使用x i （kg ），则543218.03.04.07.02.0m in x x x x x z ++++=s.t. 7001862354321≥++++x x x x x 305.022.05.054321≥++++x x x x x1008.022.05.054321≥++++x x x x x0,,,,54321≥x x x x x第二章P74-2.1(1)321532m ax y y y w ++=22321≤++y y y 243321≤++y y y 4334321=++y y y 无约束321,0,0y y y ≤≥P75-2.4(1),06353322232max 212121212121≥≥≤-≤+≤-≤++=y y y y y y y y y y y y w(2) (8/5,1/5)(3) 无穷多最优解。

清华大学《运筹学教程》胡运权主编课后习题答案

清华大学《运筹学教程》胡运权主编课后习题答案

-4 x1 1
-M x 6 2
0
x4
3
cj zj
-4
-1 0
x1
x2
x3
[3]
1
0
4
3 -1
1
20
7M-4 4M-1 -M
1
1/3 0
0 [5/3] -1
0
5/3 0
0 5M/3+1/3 -M
0 -M -M
i
x4
x5
x6
0
10
1
0
0 1 3/2
1
00
4
0
00
0 1/3 0 3
0 -4/3 1 6/5 1 -1/3 0 9/5 0 -7M/3+4/3 0
0
16/3
-7/6
(x2,x4,x6)
0
10
0
(x2,x5,x6)
0
3
0
(x3,x4,x6)
0
0
-5/2
(x3,x5,x6)
0
0
3/2
(x4,x5,x6)
0
0
0
x4
x5
x6
是否基
Z
可行解
0
0
0
否
-7
0
0
否
0
7/2
0
是
3
0
0
21/4
否
8
0
0
否
0
8
0
是
3
0
0
3
否
3
5
0
是
0
-2
0
15/4
否
0
2
9/4

第四版运筹学部分课后习题解答

第四版运筹学部分课后习题解答

运筹学部分课后习题解答P47 用图解法求解线性规划问题a）12121212min z=23466 ..424,0x xx xs t x xx x++≥⎧⎪+≥⎨⎪≥⎩解：由图1可知，该问题的可行域为凸集MABCN，且可知线段BA上的点都为最优解，即该问题有无穷多最优解，这时的最优值为min3z=23032⨯+⨯= P47 用图解法和单纯形法求解线性规划问题a）12121212max z=10x5x349 ..528,0x xs t x xx x++≤⎧⎪+≤⎨⎪≥⎩<解：由图1可知，该问题的可行域为凸集OABCO，且可知B点为最优值点，即112122134935282xx xx x x=⎧+=⎧⎪⇒⎨⎨+==⎩⎪⎩，即最优解为*31,2Tx⎛⎫= ⎪⎝⎭这时的最优值为max335z=101522⨯+⨯=单纯形法： 原问题化成标准型为121231241234max z=10x 5x 349..528,,,0x x x s t x x x x x x x +++=⎧⎪++=⎨⎪≥⎩ j c →105、B CB X b 1x 2x3x4x0 3x \9 3 4 1 0 04x8[5] 2 .0 1 j j C Z -105 00 0 3x 21/5 .0 [14/5] 1 -3/5 101x8/512/5 0 （1/5 j j C Z -1 0 -25 2x 3/2 0 ；1 5/14 -3/14 101x11 0-1/7 2/7 （j j C Z --5/14-25/14所以有*max 33351,,1015222Tx z ⎛⎫==⨯+⨯= ⎪⎝⎭P78 已知线性规划问题：1234124122341231234max24382669,,,0z x x x x x x x x x x x x x x x x x x x =+++++≤⎧⎪+≤⎪⎪++≤⎨⎪++≤⎪≥⎪⎩求: (1) 写出其对偶问题；（2）已知原问题最优解为)0,4,2,2(*=X ，试根据对偶理论，直接求出对偶问题的最优解。

清华大学胡运权运筹学

清华大学胡运权运筹学

cx°-cx* >0;
V是maxZ = C*X的S优解, 故 /
C*X*-C'X°>0;
Jr
(C*-C)(X*-X°)
= C(X°-X*) + C*(X*-X°)>0
page 25 7 April 2015
25
School of Management
第一章习题解答
1.11考虑线性规划问题
□
minZ =叫 +2JC2 + — 4X4
□
行域的每个顶点依次使目标函数达到最优。 鲤. 锒剎曷錄里姉取妾加下.
c广
cd
0
0
基b Xi x2
x3
d
x2 3/ 0 1
5/14
2
X4 j
-3/4
c
page 14
7 April 2 ns
Xi 1 1 0
Qi—'0
0
-2/14 ^W35
-
3/14d- i
第一章习题解答
□ □
当c/d在3/10到5/2之间时最优解为图中 的A 点；当c/d大于5/2且c大于等于0时最优解 为图中 的B点；当c/d小于3/10且d大于0时最优 解为图中
Bi. ■
规划问题的 maxZ = C1 X (AX =b
□
最优解, 证明[在x >0这两点连线
■
上的所有点也是 对于任何0 < a < 1, 两点连线」:的点¥满足:
X =aX⑴+(l-a)JT2)也是可行解, 且
CTX = CTaXG) +Cf\l-a)X(2y
=CTaXay -aCrX(2} +CrX
School of Management

运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用第四版胡运权主编课后练习答案一、线性规划1. 求解下列线性规划问题：max z = 3x1 + 2x2s.t.2x1 + x2 ≤ 8x1 + 2x2 ≤ 6x1, x2 ≥ 0答案：首先将约束条件化为标准形式，得到：max z = 3x1 + 2x2 + 0s1 + 0s2s.t.2x1 + x2 + s1 = 8x1 + 2x2 + s2 = 6x1, x2, s1, s2 ≥ 0通过单纯形法求解，得到最优解为：x1 = 2, x2 = 2，最优值为8。

2. 求解下列线性规划问题的对偶问题：min z = 2x1 + 3x2s.t.x1 + 2x2 ≥ 42x1 + x2 ≥ 6x1, x2 ≥ 0答案：原问题的对偶问题为：max z' = 4y1 + 6y2s.t.y1 + 2y2 ≤ 22y1 + y2 ≤ 3y1, y2 ≥ 0通过单纯形法求解，得到最优解为：y1 = 1, y2 = 1，最优值为10。

二、非线性规划1. 求解下列非线性规划问题：min f(x) = x^2 + 2x + 3s.t.x ∈ [0, 4]答案：首先求导数，得到f'(x) = 2x + 2。

令导数等于0，得到x = -1。

由于x ∈ [0, 4]，所以只需考虑x = 0和x = 4。

计算f(0) = 3，f(4) = 31。

因此，最小值为3，对应的x = 0。

2. 求解下列非线性规划问题：max f(x) = x^3 - 3x^2 + 4s.t.x ∈ [0, 3]答案：首先求导数，得到f'(x) = 3x^2 - 6x。

令导数等于0，得到x = 0或x = 2。

计算f(0) = 4，f(2) = 2，f(3) = 2。

因此，最大值为4，对应的x = 0。

三、整数规划1. 求解下列整数规划问题：max z = 3x1 + 2x2s.t.x1 + 2x2 ≤ 8x1, x2 ∈ Z答案：通过分支定界法求解，得到最优解为：x1 = 2, x2 = 3，最优值为10。

运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用 习题解答习题一 P46 1.1 (a)该问题有无穷多最优解，即满足210664221≤≤=+x x x 且的所有()21,x x ，此时目标函数值3=z 。

(b)用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解。

1.2(a) 约束方程组的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛--=1000030204180036312A4最优解()T x 0,0,7,0,10,0=。

(b) 约束方程组的系数矩阵⎪⎪⎭⎫ ⎝⎛=21224321A最优解Tx ⎪⎭⎫⎝⎛=0,511,0,52。

1.3(a)(1) 图解法最优解即为⎩⎨⎧=+=+8259432121x x x x 的解⎪⎭⎫⎝⎛=23,1x ，最大值235=z(2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式⎩⎨⎧=++=+++++=825943 ..00510 max 4213214321x x x x x x t s x x x x z则43,P P 组成一个基。

令021==x x得基可行解()8,9,0,0=x ，由此列出初始单纯形表 21σσ>。

5839,58min =⎪⎭⎫ ⎝⎛=θ02>σ，2328,1421min =⎪⎭⎫⎝⎛=θ0,21<σσ，表明已找到问题最优解0 , 0 , 23 1,4321====x x x x 。

最大值 235*=z(b)(1) 图解法最优解即为⎩⎨⎧=+=+524262121x x x x 的解⎪⎭⎫⎝⎛=23,27x，最大值217=z(2) 单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式1234523124125max 2000515.. 62245z x x x x x x x s t x x x x x x =+++++=⎧⎪++=⎨⎪++=⎩21=+x x 2621+x x则3P ，4P ，5P 组成一个基。

令021==x x得基可行解()0,0,15,24,5x =，由此列出初始单纯形表21σσ>。

运筹学(胡运权版)第三章运输问题课后习题答案

运筹学(胡运权版)第三章运输问题课后习题答案

P66： 8.某部门有3个生产同类产品的工厂（产地），生产的产品由4个销售点出售，各工厂A 1， A 2，A 3的生产量、各销售点B 1，B 2，B 3，B 4的销售量（假定单位为t ）以及各工厂到销售点的单位运价（元/t ）示于下表中，问如何调运才能使总运费最小？解：一、该运输问题的数学模型为：可以证明：约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解（初始调运方案）1. 最小元素法思想：优先满足运价（或运距）最小的供销业务。

其余（非基）变量全等于零。

此解满足所有约束条件，且基变量（非零变量）的个数为6（等于m+n-1=3+4-1=6).总运费为（目标函数值） ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ij ij x c Z 246685143228116410=⨯+⨯+⨯+⨯+⨯+⨯=2. 伏格尔（Vogel)法伏格尔法的基本思想：运输表中各行各列的最小运价与次小运价之差值（罚数）应尽可能地小。

运筹学基础及应用运输问题胡运权

运筹学基础及应用运输问题胡运权

x12
…
c21
c22
A2
x21
x22
…
Bn c1n
x1n c2n
x2n
产量 a1 a2
┇
Am 销量
┇
┇
┇
cm
cm
1
2
…
xm1
xm2
b1
b1
…
┇
┇
cmn
xmn
am
bn
1.运输规划问题的典例和数学模型 运输问题的求解思路
基本可行解
是
是否最优解
结束
否
换基
2.表上作业法
计算步骤： (1) 找出初始调运方案。即在(m×n)产销平衡表上给出 m+n-1个数字格。(最小元素法、西北角法或伏格尔法）
运筹学基础及应用
Operations Research
运
第三章
决
筹
胜
帷
运输问题
千
幄
里
之
之
中
Transportation Problem
外
1 运输规划问题的典例和数学模型 2 表上作业法 3 运输问题的应用
CONTENTS
目
录
1.运输规划问题的典例和数学模型
例B33，.1各某产公地司的从产两量个、产各地销A地1、的A销2将量物和品各运产往地三运个往销各地销B地1每, B件2, 物品的运费如下表所示，问：应如何调运可使总运输费用最 小？
步骤
描述
方法
第一步 求初始基行可行解（初始调运方案）
最小元素法、西 北角法、 伏格尔法
第二步
求检验数并判断是否得到最优解当非基变量的检验
数σi j全都非负(求min)时得到最优解，若存在检 验数σi j <0，说明还没有达到最优，转第三步。

运筹学胡运权二习题答案PPT课件

运筹学胡运权二习题答案PPT课件

(4增 ) 加一个变 新量的 x6,P6 =11，c6＝7；
最优解
为 x2 ： 2,x6
1,其他 3
变量 0。为
由于x1,x2,x3大于0，上面对偶问题前3个约束取等
号，故得到最优解：
y1=4/5, y2,=3/5,
y3=1, y4=0
第17页/共48页
第二章习题解答
2.8 已知线性规划问题A和B如下：
问题 A
n
min Z c j x j
影子价格
j 1
n
a1 j x j b1
y1
j1
st .
n
a2 jx j
minW 2y1 y2 2y3
y1 y2 y3 1
(1)对
偶问题st：y1y1 y2y2 y3y3
2 1
y1 0, y2无约束 , y3 0
(2)y1=y3=0,y2=1 时 对 偶 问 题 的 一 个 可 行 解 ， 目 标 函数值为1，故原问题的目标函数值小于等于1。
第13页/共48页
第二章习题解答
y2
20 3
, y3
50 3
,Z
230 3
(4) 略
第24页/共48页
第二章习题解答
2.11 已知线性规划问题：
max Z 2 x1 x2 x3
st.
x1 x2 x3 6 x1 2 x2 4
x
j
0, (
j
1, ,3)
先用单纯形法求出最优解，再分析在下列条件单独变化的情况下 最优解的变化。
0
0
CB 基 b X1
X2
X3
X4
X5
2 X1 6 1
0
-1
4

清华大学《运筹学教程》胡运权主编课后习题答案(第一章)

清华大学《运筹学教程》胡运权主编课后习题答案(第一章)

2)c=0
3)c>0
d<0 d=0 d>0
0
c 3 d 4
A1点 A1点 A3点
A2A3线段
3 c 5 4 d 2
c 5 d 2 c 5 d 2
c 3 d 4
A2点
A1A2线段 A1点
l.6 考虑下述线性规划问题：
max Z c1 x1 c2 x2 a11 x1 a12 x2 b1 st .a21 x1 a22 x2 b2 x1 , x2 0
-1
x2
0
x3
0
x4
-M
x5
-M
x6
CB
xB
x5
x6
x4
i
-M -M 0
3 6 4
[3] 4 1
1 3 2
0 -1 0
0 0 1
1 0 0
0 1 0 0
1 3/2 4 3 6/5 9/5
cj zj
7M-4
1 2 3 1 0 0 0
4M-1
1/3 [5/3] 5/3
5M/3+1/3
-M
0 -1 0 -M
0
0 0 1 0
0
1/3 -4/3 -1/3
-7M/3+4/3
-4 -M 0
x1
0
1 0 0
x6
x4
cj zj
cj
x6
是否基 可行解
Z
(x1,x2,x3)
(x1,x2,x4) (x1,x2,x5) (x1,x2,x6)
0
0 0 7/4
61/3
10 3 -4
-7/6
0 0 0

运筹学基础与应用(第一二章习题解答)

运筹学基础与应用(第一二章习题解答)

运筹学基础及应用 习题解答习题一 P46 1.1 (a)该问题有无穷多最优解，即满足210664221≤≤=+x x x 且的所有()21,x x ，此时目标函数值3=z 。

(b)用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解。

1.2(a) 约束方程组的系数矩阵4⎪⎪⎪⎭⎫ ⎝⎛--=1000030204180036312A最优解()T x 0,0,7,0,10,0=。

(b) 约束方程组的系数矩阵⎪⎪⎭⎫⎝⎛=21224321A最优解Tx ⎪⎭⎫⎝⎛=0,511,0,52。

1.3 (a) (1) 图解法最优解即为⎩⎨⎧=+=+8259432121x x x x 的解⎪⎭⎫⎝⎛=23,1x ，最大值235=z(2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 ⎩⎨⎧=++=+++++=825943 ..00510 max 4213214321x x x x x x t s x x x x z则43,P P 组成一个基。

令021==x x得基可行解()8,9,0,0=x ，由此列出初始单纯形表21σσ>。

5839,58min =⎪⎭⎫ ⎝⎛=θ02>σ，2328,1421min =⎪⎭⎫ ⎝⎛=θ 新的单纯形表为0,21<σσ，表明已找到问题最优解0 , 0 , 231,4321====x x x x 。

最大值 235*=z(b) (1) 图解法最优解即为⎩⎨⎧=+=+524262121x x x x 的解⎪⎭⎫⎝⎛=23,27x ，最大值217=z(2) 单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式1234523124125max 2000515.. 62245z x x x x x x x s t x x x x x x =+++++=⎧⎪++=⎨⎪++=⎩则3P ，4P ，5P 组成一个基。

令021==x x得基可行解()0,0,15,24,5x =，由此列出初始单纯形表21=+x x 2621+x x21σσ>。

(完整版)运筹学基础及应用第四版胡运权主编课后练习答案【精】

(完整版)运筹学基础及应用第四版胡运权主编课后练习答案【精】

运筹学基础及应用习题解答习题一P461.1(a)x244x1 2 x243210123x14x1 6 x26该问题有无量多最优解，即满足 4 x16x26且0x21x1 ,x2，此时目标函数值的所有2z 3 。

(b)x232014x1用图解法找不到满足所有拘束条件的公共范围，因此该问题无可行解。

1.2(a)拘束方程组的系数矩阵1236300A814020300001基基解可否基可行解目标函数值x1x2x3x4x5x6p1p 2p30167000否3-6p1p 2p 40 100700是10p1p 2p503007是3 2p1p 2p 67400021否44p1p3p4005800否2p1p3p5003080是3 2p1p3p6101003否2p1p 4p50 00350是0p1p 4p 65002015否44最优解 x0,10,0,7,0,0T。

(b)拘束方程组的系数矩阵1 2 34A2 2 12基基解x1x2x3x4p1p241100 2p1p3201155p1p41001136p2p30120 2p2p 40102 2p3p 40011211T,0最优解 x,0,。

551.3(a)(1)图解法可否基可行解目标函数值否是435否是5否是5x 24 3 2 1 0123x 1最优解即为3x 1 4x 29的解 x1,3，最大值 z355x 1 2 x 2 822(2) 单纯形法第一在各拘束条件上增加废弛变量，将问题转变为标准形式 max z10x 1 5x 2 0 x 3 0x 43x 1 4x 2 x 39 s.t.5x 1 2x 2x 48则 P 3 , P 4 组成一个基。

令 x 1 x 2 0 得基可行解 x 0,0,9,8 ，由此列出初始单纯形表c j105 0 0c B 基 bx 1x 2x 3x 40 x 3 9 3410 x 4 8[ 5] 2 0 1 c jz j10512。

min 8 ,985 35c j105 0 0 c B 基bx 1x 2x 3x 4x 321 0143551510x 18 12 01 555c j z j0 1 0 20 ，21 8 32min ,214 2新的单纯形表为c j105 0 0 c B基b x 1x 2x 3x 45x 23 015 3 2141410x 1111 277c jz j5 2514141 ,2 0 ，表示已找到问题最优解 x 1 1, x 23 , x 3 0 , x4 0 。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

运筹学基础及应用 习题解答习题一 P46 1.1 (a)该问题有无穷多最优解，即满足210664221≤≤=+x x x 且的所有()21,x x ，此时目标函数值3=z 。

(b)用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解。

1.2(a) 约束方程组的系数矩阵4⎪⎪⎪⎭⎫ ⎝⎛--=1000030204180036312A最优解()T x 0,0,7,0,10,0=。

(b) 约束方程组的系数矩阵⎪⎪⎭⎫⎝⎛=21224321A最优解Tx ⎪⎭⎫⎝⎛=0,511,0,52。

1.3 (a) (1) 图解法最优解即为⎩⎨⎧=+=+8259432121x x x x 的解⎪⎭⎫⎝⎛=23,1x ，最大值235=z(2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 ⎩⎨⎧=++=+++++=825943 ..00510 max 4213214321x x x x x x t s x x x x z则43,P P 组成一个基。

令021==x x得基可行解()8,9,0,0=x ，由此列出初始单纯形表21σσ>。

5839,58min =⎪⎭⎫ ⎝⎛=θ02>σ，2328,1421min =⎪⎭⎫ ⎝⎛=θ 新的单纯形表为0,21<σσ，表明已找到问题最优解0 , 0 , 231,4321====x x x x 。

最大值 235*=z(b) (1) 图解法最优解即为⎩⎨⎧=+=+524262121x x x x 的解⎪⎭⎫⎝⎛=23,27x ，最大值217=z(2) 单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式1234523124125max 2000515.. 62245z x x x x x x x s t x x x x x x =+++++=⎧⎪++=⎨⎪++=⎩则3P ，4P ，5P 组成一个基。

令021==x x得基可行解()0,0,15,24,5x =，由此列出初始单纯形表21=+x x 2621+x x21σσ>。

245min ,,461θ⎛⎫=-= ⎪⎝⎭02>σ，1533min ,24,522θ⎛⎫== ⎪⎝⎭新的单纯形表为0,21<σσ，表明已找到问题最优解11x =，27 2x =，3152x =，40x =，50x =。

最大值 *172z = 1.6(a) 在约束条件中添加松弛变量或剩余变量，且令()0,0 ''2'2''2'22≥≥-=x x x x x ，z z x x -=-=' ,3'3该问题转化为⎪⎪⎩⎪⎪⎨⎧≥=-+-=---+=++-+++-+--=0,,,,,633824124332x ..0023' max 54'3''2'21'3''2'215'3''2'214'3''2'2154'3''2'21x x x x x x x x x x x x x x x x x x x t s x x x x x x z其约束系数矩阵为⎪⎪⎪⎭⎫⎝⎛------=003113102114014332A在A 中人为地添加两列单位向量87,P P ⎪⎪⎪⎭⎫ ⎝⎛------100031130110211400014332 令7654'3''2'210023' max Mx Mx x x x x x x z --++-+--= 得初始单纯形表(b) 在约束条件中添加松弛变量或剩余变量，且令()''''''333330,0x x x x x =-≥≥，'z z =-该问题转化为'''123345'''12334'''12335'''1233'''123345max '3500x 2623316.. 5510,,,,,0z x x x x x x x x x x x x x x x s t x x x x x x x x x x =--+-++⎧++--=⎪+--+=⎪⎨++-=⎪⎪≥⎩其约束系数矩阵为121110************A --⎛⎫⎪=-- ⎪⎪-⎝⎭在A 中人为地添加两列单位向量87,P P121110102133010011550001--⎛⎫ ⎪- ⎪ ⎪-⎝⎭令'''12334567max '3500z x x x x x x Mx Mx =--+-++-- 得初始单纯形表1.7(a)解1：大M 法在上述线性规划问题中分别减去剩余变量468,,,x x x 再加上人工变量579,,,x x x 得123456789max 22000z x x x x Mx x Mx x Mx =-++-+-+-1234513672389123456789622,,20,,,,,,,,0x x x x x x x x x s t x x x x x x x x x x x x x ++-+=⎧⎪-+-+=⎪⎨--+=⎪⎪≥⎩其中M 是一个任意大的正数。

据此可列出单纯形表由单纯形表计算结果可以看出，40σ>且40(1,2,3)i a i <=，所以该线性规划问题有无界解解2：两阶段法。

现在上述线性规划问题的约束条件中分别减去剩余变量468,,,x x x 再加上人工变量579,,,x x x 得第一阶段的数学模型据此可列出单纯形表第一阶段求得的最优解*T 377X (,,,0,0,0,0,0,0)442=,目标函数的最优值*0ω=。

因人工变量5790x x x ===，所以*T 377(,,,0,0,0,0,0,0)442X =是原线性规划问题的基可行解。

于是可以进行第二阶段运算。

将第一阶段的最终表中的人工变量取消，并填入原问题的目标函数的系数，进行第二阶段的运算，见下表。

由表中计算结果可以看出，40σ>且40(1,2,3)i a i <=，所以原线性规划问题有无界解。

(b)解1：大M 法在上述线性规划问题中分别减去剩余变量468,,,x x x 再加上人工变量579,,,x x x 得1234567min 2300z x x x x x Mx Mx =+++++-123461257123456789428326,,,,,,,,,,0x x x x x x x x x s t x x x x x x x x x ++-+=⎧⎪+-+=⎪⎨⎪⎪≥⎩其中M 是一个任意大的正数。

据此可列出单纯形表由单纯形表计算结果可以看出，最优解*T (,,0,0,0,0,0)55X =，目标函数的最优解值*4923755z =⨯+⨯=。

X 存在非基变量检验数30σ=，故该线性规划问题有无穷多最优解。

解2：两阶段法。

现在上述线性规划问题的约束条件中分别减去剩余变量45,,x x 再加上人工变量67,,x x 得第一阶段的数学模型67min x x ω=+123461257123456789428326,,,,,,,,,,0x x x x x x x x x s t x x x x x x x x x ++-+=⎧⎪+-+=⎪⎨⎪⎪≥⎩ 据此可列出单纯形表第一阶段求得的最优解*T (,,0,0,0,0,0)55X =,目标函数的最优值*0ω=。

因人工变量670x x ==，所以T49(,,0,0,0,0,0)55是原线性规划问题的基可行解。

于是可以进行第二阶段运算。

将第一阶段的最终表中的人工变量取消，并填入原问题的目标函数的系数，进行第二阶段的运算，见下表。

由单纯形表计算结果可以看出，最优解*T (,,0,0,0,0,0)55X =，目标函数的最优解值*4923755z =⨯+⨯=。

由于存在非基变量检验数30σ=，故该线性规划问题有无穷多最优解。

1.8表1-23表1-241.10最后一个表为所求。

习题二 P76 2.1 写出对偶问题 (a)⎪⎪⎩⎪⎪⎨⎧≥=++≤+++≥++++=无约束3213214321321321,0,534332243 ..422 min x x x x x x y x x x x x x t s x x x z 对偶问题为：⎪⎪⎩⎪⎪⎨⎧≤≥=++≤++≤++++=无约束321321321321321,0,0433424322 ..532max y y y y y y y y y y y y t s y y y w (b)⎪⎪⎩⎪⎪⎨⎧≤≥≤++≥-+-=++++=0,0,837435522 ..365max 321321321321321x x x x x x x x x x x x t s x x x z 无约束 对偶问题为： ⎪⎪⎩⎪⎪⎨⎧≥≤≤+-≥++=+-++=0,0,332675254 ..835 min 321321321321321y y y y y y y y y y y y t s y y y w 无约束 2.2(a)错误。

原问题存在可行解，对偶问题可能存在可行解，也可能无可行解。

(b)错误。

线性规划的对偶问题无可行解，则原问题可能无可行解，也可能为无界解。

(c)错误。

(d)正确。

2.6 对偶单纯形法(a)⎪⎩⎪⎨⎧≥≥+≥+++=0,,522 33 ..18124 min 3213231321x x x x x x x t s x x x z 解：先将问题改写为求目标函数极大化，并化为标准形式()⎪⎩⎪⎨⎧=≥-=+---=+--++---=5,,10522 3 3 ..0018124'max 53243154321 i x x x x x x x t s x x x x x z i列单纯形表，用对偶单纯形法求解，步骤如下最优解为Tx ⎪⎭⎫ ⎝⎛=23,1,0， 目标值39=z 。

(b)⎪⎩⎪⎨⎧≥≥++≥++++=0,,1053642 3 ..425 min 321321321321x x x x x x x x x t s x x x z 解：先将问题改写为求目标函数极大化，并化为标准形式()⎪⎩⎪⎨⎧=≥-=+----=+---++---=5,,101053642 3 ..00425'max 5321432154321 i x x x x x x x x x t s x x x x x z i列单纯形表，用对偶单纯形法求解最优解为()T x 2,0,0=， 目标值8=z 。