第39讲统计量和常用统计量

统计量公式统计量是一种用于描述和总结数据集的数值指标或函数。

它们可以对数据进行量化和比较，从而得到有关数据分布和关系的信息。

以下是一些常见的统计量和它们的公式：1.平均数（Mean）：平均数是一组数据的总和除以数据的个数。

公式为：μ = (x₁ + x₂ + ... + xₙ) / n，其中x₁，x₂，...，xₙ为数据集中的观测值，n为观测值的个数。

拓展：除了算术平均数，还有几种不同的平均数，如加权平均数、几何平均数和调和平均数。

2.中位数（Median）：中位数是将一组数据按升序或降序排列后，位于中间位置的观测值。

若数据个数n为奇数，则中位数为第(n+1)/2个观测值；若n为偶数，则中位数为第n/2和n/2+1个观测值的平均值。

拓展：除了中位数，还有四分位数、百分位数等分位数，从而可以描述数据的分布和位置。

3.方差（Variance）：方差衡量了数据集的离散程度，它表示每个观测值与平均值之间的差异的平方的平均值。

公式为：σ² = Σ (xᵢ- μ)² / n，其中xᵢ为观测值，μ为平均数，n为观测值的个数。

拓展：方差的开平方称为标准差，它将方差的测量单位换成了与原始观测值相同的单位，更易于解释和比较。

4.相关系数（Correlation coefficient）：相关系数衡量了两个变量之间的线性关系的强度和方向。

常用的是皮尔逊相关系数，其公式为：r = Σ (xᵢ - μₓ)(yᵢ - μᵧ) / (nσₓσᵧ)，其中xᵢ和yᵢ为两个变量的观测值，μₓ和μᵧ为两个变量的平均值，σₓ和σᵧ为两个变量的标准差。

拓展：除了皮尔逊相关系数，还有斯皮尔曼等级相关系数和判定系数等其他类型的相关系数。

这些统计量广泛用于统计学和数据分析中，可以帮助我们理解和解释数据的特征和关系。

同时，也有其他更多的统计量公式和概念，根据不同的数据类型和问题，可以选择适当的统计量来进行分析。

.统计量
统计量是统计理论中用来对数据进行分析、检验的变量。

宏观量是大量微观量的统计平均值，具有统计平均的意义，对于单个微观粒子，宏观量是没有意义的．相对于微观量的统计平均性质的宏观量也叫统计量．需要指出的是，描写宏观世界的物理量例如速度、动能等实际上也可以说是宏观量，但宏观量并不都具有统计平均的性质，因而宏观量并不都是统计量．
数理统计的基本概念。

指不含未知参数的样本函数。

如样本x 1，x 2，…，x n的算术平均数(样本均值)＝1n(x 1+x 2+…+x n)就是一个统计量。

从样本构造统计量，实际上是对样本所含总体的信息提炼加工；根据不同的推断要求，可以构造不同的统计量。

统计量有众数，平均数，中位数等等
2.抽样分布
统计量是样本的函数，它是一个随机变量。

统计量的分布称为抽样分布。

它可分为正态总体下与非正态总体下两种情况来讨论。

是由样本n个观察值计算的统计量的概率分布。

从一个总体中随机抽出容量相同的各种样本，从这些样本计算出的某统计量所有可能值的概率分布，称为这个统计量的抽样分布。

简单随机抽样，系统抽样，分层抽样。

具体的去查高三数学最后一册吧，实在是太复杂了：）。

4.统计量的概念样本是总体的代表和反映，也是统计推断的依据．为了对总体的分布或数字特征进行各种统计推断，还需要对样本作加工处理，把样本中应关心的事物和信息集中起来，针对不同的问题构造出样本的不同函数，这种样本的函数我们称其为统计量．统计量的定义.由样本（X1, X2,…, X n）所确定的函数f(X1, X2,…, X n)称为统计量．若(x1, x2,…, x n)是一个样本观测值，则称f(x1, x2,…, x n)是统计量f(X1, X2,…, X n)的一个观测值．显然，统计量不仅是一个随机变量，而且还不含有未知参数．例3.6.4设(X1，X2，X3)是由服从正态分布Ｎ(μ,σ2)的总体X中抽取的一个容量为3的样本，其中μ、σ是未知参数，因此(X1+X2+X3)/3-μ，(X1+X2+X3)/σ都不是统计量，而X1+X2+5，X12+X22都是统计量．设（X1, X2,…, X n）是总体X中的一个样本，下面是数理统计中常用的几个统计量及其观测值：(1)样本均值.;它的观测值为：.(2)样本方差.;它的观测值为.(3)样本标准差.;它的观测值为.例3.6.5 为了了解某一课程自学考试的情况, 现从全体考生中抽查120名学生，记录其成绩如下：试按下列要求进行简单的统计分析.(1)在区间[40,100]之间，将数据分成组距为5分的12组，在此条件下，求频数分布、频率分布、累计频率分布；(2)求样本均值与样本方差；(3)作图:修正后的频率直方图、累计频率直方图．解. (1)根据已知数据，把频数分布、频率分布、累计频率分布列成表如下（(除了最后一组外，每组不包括上限)． (2)样本均值和样本方差的观测值分别是,(3)根据取值区间及相应频率作修正后的频率直方图和累计频率直方图.有了统计量的概念以后，下面我们再介绍几个在应用中有重要作用的常用的分布．实验题：学习者可以随机抽取某科考试成绩进行如下统计推断.(1) 先把数据分组,在此条件下,求频数分布、频率分布、累计频率分布;(2) 求样本均值与样本方差;(3) 画出频率直方图和累计频率直方图.。

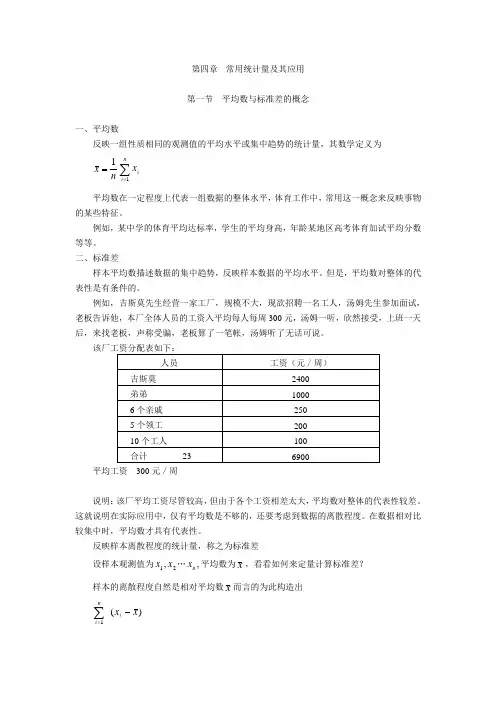
第四章 常用统计量及其应用第一节 平均数与标准差的概念一、平均数反映一组性质相同的观测值的平均水平或集中趋势的统计量，其数学定义为nx 1=∑=ni ix1平均数在一定程度上代表一组数据的整体水平，体育工作中，常用这一概念来反映事物的某些特征。

例如，某中学的体育平均达标率，学生的平均身高，年龄某地区高考体育加试平均分数等等。

二、标准差样本平均数描述数据的集中趋势，反映样本数据的平均水平。

但是，平均数对整体的代表性是有条件的。

例如，吉斯莫先生经营一家工厂，规模不大，现欲招聘一名工人，汤姆先生参加面试，老板告诉他，本厂全体人员的工资入平均每人每周300元，汤姆一听，欣然接受，上班一天后，来找老板，声称受骗，老板算了一笔帐，汤姆听了无话可说。

平均工资 300元／周说明：该厂平均工资尽管较高，但由于各个工资相差太大，平均数对整体的代表性较差。

这就说明在实际应用中，仅有平均数是不够的，还要考虑到数据的离散程度。

在数据相对比较集中时，平均数才具有代表性。

反映样本离散程度的统计量，称之为标准差设样本观测值为21,x x …,n x 平均数为x ，看看如何来定量计算标准差？ 样本的离散程度自然是相对平均数x 而言的为此构造出)(1x x i ni -∑=但上式各项有正有负，正负抵消)(1x x i ni -∑=＝0所以要反映离散程度的大小可以让上式各项加以绝对值或求平方，但带绝对值后不便于处理，所以，选择后者从而有21)(x x i ni -∑=上式与样本含量的大小有关，所以，求平均的n121)(x x i ni -∑=在实际应用中，上式对总体离散程度的估计往往偏小若以自由度（1-n ）代替n ，则是无偏的因此，构造221ˆ)(11s x x n in i =--∑= 上式中2s 称为样本方差，还原成原来的量纲 则有21)(11x x n S i ni --=∑= S 称为标准差，反映样本的离散程度。

结束语：样本平均数反映样本数据的整体水平，但是要结合标准差，标准差反映样本数据的离散程度对于运动成绩，表现为成绩的稳定性。

总结统计量什么是统计量在统计学中，统计量是用来总结和描述数据分布特征的量。

它是数据样本的函数，通过对数据进行计算和处理，可以得到一些指标来揭示数据的统计特征。

常见的统计量包括平均值、中位数、方差、标准差、最大值、最小值等等。

常用的总结统计量平均值平均值是最常见的总结统计量之一。

它是一组数据值的算术平均值，通常用符号 $\\overline{x}$ 表示。

计算平均值的方法是将所有数据值相加，然后除以数据的个数。

\begin{equation} \overline{x} = \frac{1}{n}\sum_{i=1}^{n}x_i \end{equation} 其中，x i代表第 i 个数据值，n 代表数据的个数。

平均值可以直观地反映数据的集中趋势。

中位数中位数是按照数据从小到大的顺序排列后，处于中间位置的数值。

它可以用来反映数据的中心位置。

当数据的个数为奇数时，中位数就是排列后的中间值；当数据的个数为偶数时，中位数是排列后中间两个数的平均值。

计算中位数的方法是首先将数据从小到大排序，然后根据数据的个数分情况计算。

方差方差用来度量数据的离散程度。

它是数据偏离平均值的平方的平均值，通常用符号s2表示。

\begin{equation} s^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \overline{x})^2\end{equation}其中，x i代表第i 个数据值，n 代表数据的个数，$\\overline{x}$ 代表平均值。

方差的单位是原数据单位的平方。

标准差标准差是方差的平方根，用符号 s 表示。

它是衡量数据离散程度的常用指标。

标准差越大，代表数据越分散；标准差越小，代表数据越集中。

标准差的计算公式如下：\begin{equation} s = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \overline{x})^2} \end{equation}极差极差是一组数据中，最大值与最小值的差。