第四章 常用统计量的计算

统计量的计算与应用总结统计量是用来衡量数据集中的特征或者描述数据分布情况的指标。

在统计学中，通过计算各种统计量可以对数据进行描绘和分析，从而得出结论和做出决策。

本文将总结统计量的计算方法和应用。

一、均值均值是最基本的统计量之一，用来描述数据的集中趋势。

计算均值的公式是将所有数据相加然后除以总数。

均值的计算方法适用于数字型数据。

均值广泛应用于各个领域，如金融、经济学、医学等。

它可以用来描述一个样本或总体的平均水平。

二、中位数中位数是将数据按照大小顺序排列后，位于中间的数值。

如果数据个数为奇数，则中位数就是最中间的值；如果数据个数为偶数，则中位数是最中间两个数的平均值。

中位数在处理数据含有极端值或者数据分布不对称时更有稳定性，相较于均值更能反映数据的真实情况。

三、众数众数是数据集中出现次数最多的数值。

对于分类数据或存在多个峰值的连续数据，众数是一个很有用的统计量。

在市场调研、社会调查等领域中，众数常被用于描述受访者对某个问题的最常见回答。

四、标准差标准差是描述数据离散程度的统计量。

标准差越大，说明数据分布越分散；标准差越小，说明数据越集中。

标准差的计算方法包括先计算方差，然后取方差的平方根。

标准差在金融领域的风险评估、质量管理中的过程控制等方面都有重要应用。

五、偏度与峰度偏度是描述数据分布偏斜程度的统计量。

正偏表示数据分布尾部向右拉长，负偏表示数据分布尾部向左拉长。

峰度是描述数据分布峰态的统计量。

正峰表示数据分布呈现尖峭的峰态，负峰表示数据分布呈现平坦的峰态。

偏度和峰度的计算公式较为复杂，常用于判断数据的分布形状和性质。

六、相关系数相关系数用于衡量两个变量之间的线性相关性。

常用的相关系数有皮尔逊相关系数和斯皮尔曼等级相关系数。

相关系数的取值范围在-1到1之间，接近1表示正相关，接近-1表示负相关，接近0表示无相关性。

相关系数在金融、社会科学等领域具有重要应用，可以帮助我们了解变量之间的关联关系。

七、置信区间置信区间是用来估计总体参数的一个区间范围。

初中数学知识归纳统计量的计算与应用统计量是统计学中用于度量和描述数据集合特征的数值指标。

在初中数学中，我们经常会遇到统计量的计算与应用。

本文将对常见的统计量进行归纳，并介绍它们在实际问题中的应用。

一、平均数平均数是一组数据的总和除以数据的个数。

计算平均数时，首先将所有数据求和，然后除以数据的个数。

平均数常用于表示一组数据的“典型”或“平衡”值。

例如，某班级6位学生的考试分数分别为85、90、78、92、88、95。

我们可以先将这些分数相加，得到85+90+78+92+88+95=528，然后再将总分528除以学生人数6，得到平均分88。

平均数在生活中有很多应用。

比如，我们可以通过计算某商品的平均价格来了解其市场价格水平；又比如，平均年龄可以用来衡量一个国家或地区的人口结构。

二、中位数中位数是按照从小到大的顺序排列后，处于中间位置的那个数。

当数据个数为奇数时，中位数为排序后的中间值；当数据个数为偶数时，中位数为排序后中间两个数的平均值。

对于数据集合{3，7，2，9，1}，将其排序得到{1，2，3，7，9}，可以看出中间位置的数是3，因此中位数为3。

中位数在应用中经常用于衡量数据的“中心位置”，尤其对于有异常值的数据集合更具有稳定性。

比如，某公司员工的年龄数据{23，25，27，29，100}，若使用平均数来衡量，那么受到100这个异常值的影响会使平均年龄看起来很大；而计算中位数时，这个异常值并不能对结果产生显著影响。

三、众数众数是一组数据中出现频次最高的数值。

一个数据集合可能会有一个或多个众数，也可能没有众数。

比如，某班级8位学生的考试分数分别为85、90、78、92、88、95、90、90。

在这个数据集合中，90出现的频次最高，因此众数为90。

众数在统计学中常用于描述数据的“集中趋势”。

例如，通过分析一项产品销售数据中的众数，可以帮助企业了解市场需求，进而调整产品供应。

四、极差极差是一组数据的最大值减去最小值得到的差值。

统计量公式统计量是一种用于描述和总结数据集的数值指标或函数。

它们可以对数据进行量化和比较，从而得到有关数据分布和关系的信息。

以下是一些常见的统计量和它们的公式：1.平均数（Mean）：平均数是一组数据的总和除以数据的个数。

公式为：μ = (x₁ + x₂ + ... + xₙ) / n，其中x₁，x₂，...，xₙ为数据集中的观测值，n为观测值的个数。

拓展：除了算术平均数，还有几种不同的平均数，如加权平均数、几何平均数和调和平均数。

2.中位数（Median）：中位数是将一组数据按升序或降序排列后，位于中间位置的观测值。

若数据个数n为奇数，则中位数为第(n+1)/2个观测值；若n为偶数，则中位数为第n/2和n/2+1个观测值的平均值。

拓展：除了中位数，还有四分位数、百分位数等分位数，从而可以描述数据的分布和位置。

3.方差（Variance）：方差衡量了数据集的离散程度，它表示每个观测值与平均值之间的差异的平方的平均值。

公式为：σ² = Σ (xᵢ- μ)² / n，其中xᵢ为观测值，μ为平均数，n为观测值的个数。

拓展：方差的开平方称为标准差，它将方差的测量单位换成了与原始观测值相同的单位，更易于解释和比较。

4.相关系数（Correlation coefficient）：相关系数衡量了两个变量之间的线性关系的强度和方向。

常用的是皮尔逊相关系数，其公式为：r = Σ (xᵢ - μₓ)(yᵢ - μᵧ) / (nσₓσᵧ)，其中xᵢ和yᵢ为两个变量的观测值，μₓ和μᵧ为两个变量的平均值，σₓ和σᵧ为两个变量的标准差。

拓展：除了皮尔逊相关系数，还有斯皮尔曼等级相关系数和判定系数等其他类型的相关系数。

这些统计量广泛用于统计学和数据分析中，可以帮助我们理解和解释数据的特征和关系。

同时，也有其他更多的统计量公式和概念，根据不同的数据类型和问题，可以选择适当的统计量来进行分析。

统计量的计算与分析教案统计量的计算与分析一、引言统计量是统计学中用来描述和度量数据特征的工具。

在数据分析和研究中，我们经常需要计算和使用各种统计量来对数据进行描述和分析。

本教案将介绍统计量的计算方法和其在数据分析中的应用。

二、均值与方差均值是描述数据集中趋势的统计量，它表示数据的平均水平。

计算一个样本的均值，我们可以将所有数据相加并除以样本大小。

样本均值的计算公式如下：\[ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \]其中，\( \bar{x} \) 表示样本均值，\( n \) 表示样本大小，\( x_i \) 表示第 \( i \) 个观测值。

方差是衡量数据分散程度的统计量，它表示数据与均值之间的差异。

计算一个样本的方差，我们可以将每个数据与均值的差平方后相加并除以样本大小减一。

样本方差的计算公式如下：\[ s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 \]其中，\( s^2 \) 表示样本方差。

三、标准差与标准误标准差是方差的平方根，它衡量数据的离散程度。

标准差的计算公式如下：\[ s = \sqrt{s^2} \]标准误是样本均值的抽样变异度的估计。

它表示样本均值与真实总体均值的差异。

标准误的计算公式如下：\[ SE = \frac{s}{\sqrt{n}} \]其中，\( SE \) 表示标准误。

四、相关系数与回归分析相关系数是衡量两个变量之间线性关系强弱的统计量。

相关系数的计算方法有多种，其中最常用的是皮尔逊相关系数。

皮尔逊相关系数的取值范围在-1到1之间，接近-1表示负相关，接近1表示正相关，接近0表示无相关。

计算皮尔逊相关系数的公式如下：\[ r = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i -\bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2 \sum_{i=1}^{n}(y_i -\bar{y})^2}} \]其中，\( r \) 表示相关系数，\( x_i \) 和 \( y_i \) 分别表示两个变量的观测值。

统计量公式统计量是统计学中常用的概念，它用来描述和总结数据的特征和分布情况。

统计量可以帮助我们更好地理解数据，并从中提取出有用的信息。

在实际应用中，统计量是进行数据分析和推断的重要工具，它们可以帮助我们做出准确的决策和预测。

常见的统计量包括均值、中位数、众数、标准差、方差、偏度和峰度等。

下面分别介绍这些统计量的计算公式和含义。

1. 均值：均值是一组数据的平均数，用于表示数据的集中趋势。

计算公式为：均值 = 总和 / 观测值的个数。

均值可以帮助我们了解数据的平均水平，并可以用来对比不同数据集之间的差异。

2. 中位数：中位数是一组数据排序后的中间值，它能够较好地反映数据的分布情况，相对于均值更具有鲁棒性。

如果数据个数为奇数，中位数就是排序后的中间值；如果数据个数为偶数，中位数就是排序后中间两个数的平均值。

3. 众数：众数是一组数据中出现频率最高的值，用于描述数据的集中程度。

一个数据集可能存在多个众数，也可能没有众数。

4. 标准差：标准差衡量了数据的波动程度，也就是数据的离散程度。

标准差越大，数据的离散程度就越大；标准差越小，数据的离散程度就越小。

标准差的计算公式为：标准差 = 平方根（方差）。

5. 方差：方差衡量了数据的离散程度，它是各个观测值与均值之差的平方和的平均值。

方差越大，数据的离散程度也越大；方差越小，数据的离散程度也越小。

6. 偏度：偏度用于衡量数据分布的不对称程度。

如果数据分布左偏，即数据的尾部向左拉长，偏度为负数；如果数据分布右偏，即数据的尾部向右拉长，偏度为正数。

7. 峰度：峰度用于衡量数据分布的尖锐程度。

正态分布的峰度为3，如果数据分布的峰度大于3，则分布更为尖锐；如果峰度小于3，则分布较为平缓。

统计量的计算和使用可以帮助我们深入了解数据，从而做出正确的决策。

在不同的领域和问题中，我们可以根据需要选择相应的统计量来分析数据，并且可以结合其他统计方法进行更深入的研究。

同时，统计量的计算结果也需要综合考虑其他因素，如样本的大小和数据的分布特点，以保证统计结果的可靠性和有效性。

统计量的概念统计量是指用来描述和总结一组数据特征的指标，它可以帮助我们更好地理解数据的分布和特征，从而进行更深入的数据分析和推断。

在数据分析中，统计量起着至关重要的作用，它们可以帮助我们发现数据中的规律和趋势，从而为决策和预测提供依据。

本文将从统计量的概念、常见的统计量及其计算方法以及统计量在数据分析中的应用等方面进行探讨。

一、统计量的概念。

统计量是对数据的一种数值描述，它可以用来描述数据的集中趋势、离散程度、分布形状等特征。

常见的统计量包括均值、中位数、众数、标准差、方差、偏度、峰度等。

这些统计量可以帮助我们更好地理解数据的特征，从而进行更深入的数据分析和推断。

均值是一组数据的平均值，它可以反映数据的集中趋势。

中位数是一组数据中间位置的数值，它可以反映数据的位置关系。

众数是一组数据中出现次数最多的数值，它可以反映数据的分布情况。

标准差和方差是用来衡量数据的离散程度的统计量，它们可以反映数据的波动情况。

偏度和峰度是用来描述数据分布形状的统计量，它们可以反映数据的分布情况。

二、常见的统计量及其计算方法。

1. 均值的计算方法。

均值是一组数据的平均值，它可以通过以下公式进行计算：\[ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \]其中，\(\bar{x}\)表示均值，\(n\)表示数据的个数，\(x_i\)表示第\(i\)个数据。

2. 中位数的计算方法。

中位数是一组数据中间位置的数值，它可以通过以下方法进行计算：如果数据个数\(n\)为奇数，则中位数为第\(\frac{n+1}{2}\)个数据；如果数据个数\(n\)为偶数，则中位数为第\(\frac{n}{2}\)个数据和第\(\frac{n}{2}+1\)个数据的平均值。

3. 众数的计算方法。

众数是一组数据中出现次数最多的数值，它可以通过统计数据的频数来确定。

4. 标准差和方差的计算方法。

标准差和方差是用来衡量数据的离散程度的统计量，它们可以通过以下公式进行计算：\[ s = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i \bar{x})^2} \]\[ s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i \bar{x})^2 \]其中，\(s\)表示标准差，\(s^2\)表示方差，\(\bar{x}\)表示均值，\(n\)表示数据的个数，\(x_i\)表示第\(i\)个数据。

统计学中的常用统计量统计学是一门关于数据收集、分析和解释的学科，它提供了一系列的统计量来总结和描述数据的特征。

这些统计量可以帮助我们理解数据的分布、趋势和关联性。

在本文中，我们将介绍统计学中的一些常用统计量及其应用。

一、中心位置的统计量1. 均值（Mean）：均值是一组数据的平均值。

计算均值的方法是将所有观测值相加，然后除以观测值的总数。

均值对异常值非常敏感，所以在一些情况下，中位数可能更适合作为中心位置的度量。

2. 中位数（Median）：中位数是将一组数据按照大小顺序排列后的中间值。

如果数据集中的观测值为奇数个，则中位数就是中间的观测值；如果观测值为偶数个，则中位数是中间两个观测值的平均数。

中位数对异常值不敏感，因此在分析偏态数据时常常使用。

二、离散程度的统计量3. 方差（Variance）：方差衡量了数据的离散程度，计算方式为每个数据与均值之差的平方的平均值。

方差的单位是原数据单位的平方，所以为了更好地描述数据的离散程度，常用标准差作为方差的平方根。

4. 标准差（Standard Deviation）：标准差是方差的平方根，它衡量了数据相对于均值的平均偏离程度。

标准差越大，数据的离散程度越大。

5. 百分位数（Percentiles）：百分位数是将数据按照大小排序后，某个特定百分比处的数值。

例如，第25百分位数是将数据按照从小到大排序后，处于25%位置上的观测值。

三、数据分布形态的统计量6. 偏度（Skewness）：偏度衡量了数据分布的对称性。

当数据分布左偏时，偏度为负值；当数据分布右偏时，偏度为正值。

偏度为0表示数据分布对称。

7. 峰度（Kurtosis）：峰度衡量了数据分布的尖锐程度。

正态分布的峰度为3，如果峰度大于3，表示分布的尖锐程度高于正态分布；如果峰度小于3，表示分布的尖锐程度低于正态分布。

四、相关性的统计量8. 相关系数（Correlation Coefficient）：相关系数衡量了两个变量之间的线性关系强度和方向。

统计量的计算与应用统计学作为研究和分析数据的一门学科，涉及到许多计算和应用方法。

在统计学中，统计量是一种用来总结和描述数据的量化指标。

本文将介绍统计量的计算方法以及其在实际应用中的重要性。

一、统计量的计算方法1. 平均值（Mean）：平均值是最常见的统计量之一，计算公式为将所有观测值相加，然后除以观测值的数量。

平均值可以反映数据的集中趋势。

2. 中位数（Median）：中位数是将数据按大小排序后，处于中间位置的观测值。

如果数据数量为奇数，则中位数就是排序后的中间值；如果数据数量为偶数，则中位数是中间两个观测值的平均值。

中位数适用于有离群值的数据集。

3. 众数（Mode）：众数是指数据中出现频率最高的观测值。

一个数据集可能有一个或多个众数，也可能没有众数。

4. 标准差（Standard Deviation）：标准差是数据的离散程度的度量，它衡量的是每个数据点与平均值的差距。

标准差越大，数据的离散程度就越大。

5. 方差（Variance）：方差是标准差的平方，它描述了每个数据点与平均值之间的平均差异程度。

二、统计量的应用1. 描述性统计分析：统计量广泛应用于描述性统计分析中，可以帮助我们了解数据的集中趋势、离散程度和形状。

例如，通过计算平均值和标准差，我们可以得出一组数据的一般特征。

2. 推断统计分析：统计量在推断统计分析中也有着重要的应用。

通过计算样本均值和样本标准差，可以进行参数估计和假设检验，从而得出关于总体的推断。

3. 质量控制：在生产工艺中，统计量被广泛应用于质量控制。

通过监测平均值、方差和其他统计量，可以评估和改进产品的质量水平。

4. 风险分析：统计量在风险分析和金融领域也有重要应用。

例如，价值-at-风险（Value-at-Risk）是一种常用的风险测量指标，它可以帮助投资者评估投资组合的风险水平。

5. 统计模型建立：在建立统计模型时，统计量可以用于选择适当的模型、估计模型参数和评估模型拟合优度。

统计量公式范文统计量是用来描述样本或总体特征的量，可以帮助我们理解和分析数据。

不同的统计量有不同的公式和计算方法，下面将详细介绍一些常用的统计量及其公式。

1. 均值（Mean）：均值是统计样本或总体数据的中心位置的度量，用于表示数值变量的集中趋势。

对于总体来说，均值的公式为：μ=（ΣXi）/N其中，μ为总体平均值，Xi表示总体中的每个变量，Σ表示求和符号，N为总体大小。

对于样本来说，均值的公式为：x̄=（ΣXi）/n其中，x̄为样本平均值，Xi表示样本中的每个变量，Σ表示求和符号，n为样本大小。

2. 中位数（Median）：中位数是一组数据中间的值。

当数据被排序后，中位数是位于中间的值，也就是将数据分为较小和较大两部分的分界点。

对于总体来说，中位数的计算公式为：中位数=（N+1）/2对于样本来说，中位数的计算公式为：中位数=（n+1）/23. 众数（Mode）：众数是一组数据中出现次数最多的值，可以有一个或多个众数。

4. 方差（Variance）：方差是用来衡量数据的离散程度或变异程度。

方差值越大，表示数据越离散；方差值越小，表示数据越集中。

对于总体来说，方差的计算公式为：σ²=Σ（Xi-μ）²/N其中，σ²为总体方差，Σ表示求和符号，Xi表示总体中的每个变量，μ为总体平均值，N为总体大小。

对于样本来说，方差的计算公式为：s²=Σ（Xi-x̄）²/(n-1)其中，s²为样本方差，Σ表示求和符号，Xi表示样本中的每个变量，x̄为样本平均值，n为样本大小。

5. 标准差（Standard Deviation）：标准差是方差的平方根，用来度量数据的离散程度或变异程度。

对于总体来说，标准差的计算公式为：σ=√(Σ（Xi-μ）²/N)其中，σ为总体标准差，Σ表示求和符号，Xi表示总体中的每个变量，μ为总体平均值，N为总体大小。

对于样本来说s=√(Σ（Xi-x̄）²/(n-1))其中，s为样本标准差，Σ表示求和符号，Xi表示样本中的每个变量，x̄为样本平均值，n为样本大小。

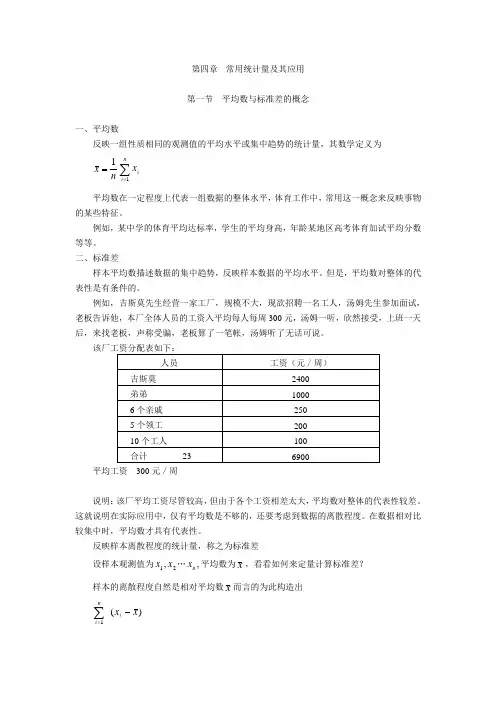
第四章 常用统计量及其应用第一节 平均数与标准差的概念一、平均数反映一组性质相同的观测值的平均水平或集中趋势的统计量，其数学定义为nx 1=∑=ni ix1平均数在一定程度上代表一组数据的整体水平，体育工作中，常用这一概念来反映事物的某些特征。

例如，某中学的体育平均达标率，学生的平均身高，年龄某地区高考体育加试平均分数等等。

二、标准差样本平均数描述数据的集中趋势，反映样本数据的平均水平。

但是，平均数对整体的代表性是有条件的。

例如，吉斯莫先生经营一家工厂，规模不大，现欲招聘一名工人，汤姆先生参加面试，老板告诉他，本厂全体人员的工资入平均每人每周300元，汤姆一听，欣然接受，上班一天后，来找老板，声称受骗，老板算了一笔帐，汤姆听了无话可说。

平均工资 300元／周说明：该厂平均工资尽管较高，但由于各个工资相差太大，平均数对整体的代表性较差。

这就说明在实际应用中，仅有平均数是不够的，还要考虑到数据的离散程度。

在数据相对比较集中时，平均数才具有代表性。

反映样本离散程度的统计量，称之为标准差设样本观测值为21,x x …,n x 平均数为x ，看看如何来定量计算标准差？ 样本的离散程度自然是相对平均数x 而言的为此构造出)(1x x i ni -∑=但上式各项有正有负，正负抵消)(1x x i ni -∑=＝0所以要反映离散程度的大小可以让上式各项加以绝对值或求平方，但带绝对值后不便于处理，所以，选择后者从而有21)(x x i ni -∑=上式与样本含量的大小有关，所以，求平均的n121)(x x i ni -∑=在实际应用中，上式对总体离散程度的估计往往偏小若以自由度（1-n ）代替n ，则是无偏的因此，构造221ˆ)(11s x x n in i =--∑= 上式中2s 称为样本方差，还原成原来的量纲 则有21)(11x x n S i ni --=∑= S 称为标准差，反映样本的离散程度。

结束语：样本平均数反映样本数据的整体水平，但是要结合标准差，标准差反映样本数据的离散程度对于运动成绩，表现为成绩的稳定性。

基本统计量的计算统计学是一门研究收集、整理、分析和解释数据的学科。

在统计学中，计算和理解基本统计量是非常重要的，它们能够帮助我们更好地理解数据集的特征和分布，从而做出准确的判断和决策。

一、平均值平均值是数据集中所有观测值的总和除以观测值的数量。

计算平均值的公式如下：平均值 = 总和 / 观测值的数量例如，有一个数据集包括以下观测值：5, 8, 6, 4, 9。

计算这些观测值的平均值，首先将它们相加得到总和：5 + 8 + 6 + 4 + 9 = 32。

然后将总和除以观测值的数量（5个）：32 / 5 = 6.4。

所以，这些观测值的平均值是6.4。

二、中位数中位数是将数据集中的观测值按照大小顺序排列后，处于中间位置的值。

如果数据集的观测值数量为奇数，则中位数就是中间位置的观测值；如果数据集的观测值数量为偶数，则中位数是中间两个观测值的平均值。

例如，有一个数据集包括以下观测值：5, 8, 6, 4, 9。

将这些观测值按照大小顺序排列：4, 5, 6, 8, 9。

这个数据集的观测值数量是奇数，中位数就是处于中间位置的观测值，即6。

三、众数众数是数据集中出现次数最多的观测值。

一个数据集可能有一个众数，也可能有多个众数，甚至没有众数。

例如，有一个数据集包括以下观测值：6, 8, 6, 4, 9。

在这个数据集中，观测值6出现了两次，而其他观测值只出现了一次，所以6是这个数据集的众数。

四、范围范围是数据集中最大观测值和最小观测值之间的差值。

计算范围的公式如下：范围 = 最大观测值 - 最小观测值例如，有一个数据集包括以下观测值：5, 8, 6, 4, 9。

这个数据集中的最大观测值是9，最小观测值是4，所以范围是9 - 4 = 5。

五、方差和标准差方差和标准差能够帮助我们了解数据集的离散程度。

方差是观测值与平均值之间差异的平方和的平均值，计算方差的公式如下：方差= ∑（观测值 - 平均值）² / 观测值的数量标准差是方差的平方根，计算标准差的公式如下：标准差= √方差方差和标准差的数值越大，表示数据集中的观测值离平均值越远，数据的离散程度就越大。

统计量的计算与解读统计学是一门研究收集、整理、分析和解释大量数据的学科。

统计量是指在统计分析中使用的数值度量，用于总结和描述数据的特征。

本文将介绍统计量的计算方法和解读，并探讨其在实际应用中的意义。

一、均值均值是统计学中最常用的统计量，用于表示数据的集中趋势。

计算均值的方法是将所有观测值相加，然后除以观测值的个数。

均值的计算公式如下：均值 = (观测值1 + 观测值2 + ... + 观测值n) / n通过计算均值，我们可以得出数据的平均水平，进而对数据进行比较和推断。

例如，在一项市场调研中，我们可以计算出某个产品的平均满意度，从而评估其市场竞争力。

二、中位数中位数是统计学中描述数据的另一个常用统计量，用于表示数据的中间位置。

计算中位数的方法是将数据按照大小进行排序，然后取中间位置的观测值作为中位数。

如果数据个数为奇数，中位数即为排序后的中间值；如果数据个数为偶数，中位数则为排序后中间两个值的平均值。

中位数的计算方法简单直观，能够较好地反映数据的典型特征。

例如，在一组收入数据中，中位数可以用来表示人群的收入水平，较为准确地反映出整体的收入情况。

三、众数众数是指在数据中出现频率最高的数值，反映了数据分布的集中程度。

众数的计算方法是统计各个数值出现的频次，然后找出频次最高的数值作为众数。

众数在处理离散型数据时具有重要意义。

例如，在一组考试成绩中，众数可以帮助我们了解哪个成绩分数出现的次数最多，进而了解哪个分数段的学生占比较高。

四、方差方差是统计学中衡量数据变异程度的统计量，用于反映数据的离散程度。

方差的计算方法是将每个观测值与均值的差值进行平方，然后求平均值。

方差越大，说明数据的波动性越高，反之则说明数据的波动性较低。

例如，在研究某个投资组合的风险时，方差可以用来评估该投资组合的波动性和不确定性。

五、标准差标准差是方差的平方根，用于衡量数据的离散程度。

标准差的计算方法是对方差进行开方。

标准差是一种常用的度量指标，可以帮助我们判断数据的稳定性和可靠性。

求统计量的方法总结统计学是一门研究如何从数据中提取有效信息的学科。

在进行统计分析时，我们通常需要根据数据的特点和目标来选择相应的统计量。

本文将对常见的统计量和计算方法进行总结。

一、中心位置的统计量中心位置的统计量用于描述数据集的集中程度，常见的统计量包括均值、中位数和众数。

1. 均值（Mean）是指将所有观察值相加后再除以观测值的数量。

计算公式：均值 = 总和 / 观测值数量。

2. 中位数（Median）是指将数据按照大小排序后，位于中间位置的值。

若观测值数量为奇数，则中位数即为中间值；若为偶数，则中位数为中间两个数的平均值。

3. 众数（Mode）是指在数据集中出现频率最高的值。

二、离散程度的统计量离散程度的统计量用于描述数据集的分散程度，常见的统计量包括方差、标准差和极差。

1. 方差（Variance）是指观测值与均值之间的差异程度的平均值。

计算公式：方差= (∑(观测值-均值)^2) / 观测值数量。

2. 标准差（Standard Deviation）是方差的算术平方根，用于衡量观测值离均值的平均距离。

3. 极差（Range）是指数据集中最大值与最小值之间的差异。

计算公式：极差 = 最大值 - 最小值。

三、数据分布的统计量数据分布的统计量用于描述数据集的分布形态，常见的统计量包括偏度和峰度。

1. 偏度（Skewness）用于描述数据分布的偏斜程度。

偏度为正表示分布向右偏斜，为负表示分布向左偏斜，为0表示分布对称。

2. 峰度（Kurtosis）用于描述数据分布的尖峰程度。

高峰度表示分布曲线较陡峭，低峰度表示分布曲线较平缓。

四、相关性的统计量相关性的统计量用于描述两个或多个变量之间的关联程度，常见的统计量包括相关系数和回归分析。

1. 相关系数（Correlation Coefficient）用于衡量变量之间线性相关的强度和方向。

常用的相关系数有皮尔逊相关系数、斯皮尔曼相关系数和切比雪夫相关系数等。