《曲边梯形的面积定积分》练习题.doc

预习导航1．函数的极值(1)已知函数y＝f(x)，设x0是定义域(a，b)内任一点，如果对x0附近的所有点x，都有f(x)＜f(x0)，则称函数f(x)在点x0处取极大值，记作y极大＝f(x0)，并把x0称为函数f(x)的一个极大值点．如果在x0附近都有f(x)＞f(x0)，则称函数f(x)在点x0处取极小值，记作y极小＝f(x0)，并把x0称为函数f(x)的一个极小值点．(2)极大值与极小值统称为极值，极大值点与极小值点统称为极值点．思考1 (1)极大值(极小值)是否就是函数在定义域内最大的值(最小的值)?(2)函数是否一定存在极值？若存在，是否是唯一的？(3)极大值是否一定比极小值大？(4)函数的极值点是否可以出现在区间的端点？提示：(1)极值是一个局部概念．由定义知，极值只是某个点的函数值与它附近点的函数值比较是最大或最小，并不意味着它在函数的整个定义域内最大或最小．(2)在一个给定的区间上，函数可能存在若干个极值，也可能不存在极值；函数可以只有极大值，没有极小值，或者只有极小值没有极大值，也可能既有极大值，又有极小值．(3)极大值与极小值之间无确定的大小关系，即一个函数的极大值未必大于极小值．(4)不可以，函数在一个区间的端点处一定不可能取得极值，因为不符合极值点的定义．2．求函数y＝f(x)极值的步骤第1步：求导数f′(x)；第2步：求方程f′(x)＝0的所有实数根；第3步：考察在每个根x0附近，从左到右，导函数f′(x)的符号如何变化．如果f′(x)的符号由正变负，则f(x0)是极大值；如果由负变正，则f(x0)是极小值．如果在f′(x)＝0的根x＝x0的左、右侧，f′(x)的符号不变，则f(x0)不是极值．思考2 (1)导数为0的点一定是函数的极值点吗？(2)函数在极值点处的导数一定等于0吗？提示：(1)不一定，例如对于函数f(x)＝x3，虽有f′(0)＝0，但x＝0并不是f(x)＝x3的极值点，要使导数为0的点成为极值点，还必须满足其他条件．(2)不一定，例如函数f(x)＝|x－1|，它在x＝1处取得极小值，但它在x＝1处不可导，就更谈不上导数等于0了．但对可导函数来说，极值点处的导数值一定等于0.3．函数的最值函数f(x)的最大(小)值是函数在指定区间上的最大(小)的值．点拨函数极值与最值的联系与区别：(1)函数的极值是表示函数在某一点附近的变化情况，是在局部上对函数值的比较，具有相对性；而函数的最值则是表示函数在整个定义区间上的情况，是对整个区间上的函数值的比较，具有绝对性．(2)函数在一个闭区间上若存在最大值或最小值，则最大值或最小值最多只能各有一个，具有唯一性；而极大值和极小值可能多于一个，也可能没有，例如：常函数就没有极大值，也没有极小值．(3)极值只能在函数的定义域内部取得，而最值可以在区间的端点处取得．有极值的不一定有最值，有最值的不一定有极值，极值有可能成为最值，最值只要不是在端点处取到，则一定是某个极值．4．求函数y＝f(x)在[a，b]上的最大(小)值的步骤第1步：求f(x)在开区间(a，b)内所有使f′(x)＝0的点．第2步：计算函数f(x)在区间(a，b)内使f′(x)＝0的所有点和端点的函数值，其中最大的一个为最大值，最小的一个为最小值．思考3如果函数f(x)在闭区间[a，b]上是单调函数，如何求其最值？提示：如果函数f(x)在闭区间[a，b]上恰好是单调函数，那么函数的最值恰好在两个端点处取到．当f(x)在闭区间[a，b]上递增时，f(a)是最小值，f(b)是最大值；当f(x)在闭区间[a，b]上递减时，f(a)是最大值，f(b)是最小值．点拨函数f(x)在开区间上最值的求法：如果要研究函数在开区间上的最值情况，那么就要与闭区间加以区别．由于是开区间，所以函数的最值不能在端点处取得，而只能在极值点处取得，当函数在开区间上只有一个极值时，这个极值也必然是最值．如果在无穷区间(－∞，＋∞)上函数只有一个极值，那么这个极值也就是最值．此外，还要注意研究函数值的变化趋势，必要时应画出函数的大致图象，结合图象分析函数的最值．。

自主广场我夯基 我达标1.在求由x=a,x=b(a ＜b),y=f(x)［f(x)≥0］及y=0围成的曲边梯形的面积S 时，在区间［a,b ］上等间隔地插入n-1个分点，分别过这些分点作x 轴的垂线，把曲边形分成n 个小曲边形，下列说法中正确的个数是( )①n 个小曲边形的面积和等于S②n 个小曲边形的面积和小于S③n 个小曲边形的面积和大于S④n 个小曲边形的面积和与S 之间的大小关系无法确定A.1B.2C.3D.4思路解析：根据“化整为零”“积零为整”的思想，知①是正确的.答案:A2.函数f(x)=x 2在区间［ni n i ,1-］上,则( ) A.f(x)的值变化很小 B.f(x)的值变化很大C.f(x)的值不变化D.当n 很大时，f(x)的值变化很小思路解析：因为分割得越细，越接近原函数值，所以当n 很大时，f(x)的值变化很小. 答案:D3.设函数f(x)在区间［a,b ］上连续，用分点a=x 0＜x 1＜…＜x i-1＜x i ＜…＜x n =b ，把区间［a,b ］等分成n 个小区间，在每个小区间［x i-1,x i ］上任取一点ξi (i=1,2,…,n)，作和式I n =∑=n i i f 1)(ξΔx(其中Δx 为小区间的长度)那么I n的大小( ) A.与f(x)和区间［a,b ］有关，与分点的个数n 和ξi 的取法无关B.与f(x)、区间［a,b ］和分点个数n 有关，与ξi 的取法无关C.与f(x)、区间［a,b ］和ξi 的取法有关，与分点的个数n 无关D.与f(x)、区间［a,b ］、分点的个数n 、ξi 的取法都有关思路解析：根据定积分的定义可知n 越大即分点越多，与f(x)的值越接近，与ξi 的取法也有关.答案:D4.⎰10dx 等于( ) A.0 B.1 C.21 D.2 思路解析：1010|x dx =⎰,故⎰10dx =1. 答案:B5.下列等式成立的是( )A.⎰-=b a a b xdx 0 B.⎰=b a xdx 21 C.⎰⎰=-1011||2||dx x dx x D.⎰⎰=+b a ba xdx dx x )1(思路解析：根据定积分的定义可知⎰⎰=-1011||2||dx x dx x . 答案:C我综合 我发展6.计算定积分⎰-50.)63(dx x 思路分析：利用定积分的定义和性质求解.解：如下图，计算可得A 的面积为227，B 的面积为6，从而 2156227)63(50=-=-⎰dx x .7.利用定积分求n 趋近于+∞时121++++ααααnn (α＞0)的值. 思路分析：根据定积分的定义和性质求解.解：∑=+•=+++n i n ni n n 111)(21ααααα =αααα+=•+=+⎰11|1110110x dx x .。

X曲边梯形面积与定积分得分 ________一、选择题(共12小题，每小题5分,共60分) 21.函数y=x cosx 的导数,,,,,,,,,,,,,,, 【A. y =2xcosx — x 1 2s inx2 .B. y =2xcosx+x snx2C. y' =x cosx — 2xsi nx 2 .D. y =xcosx — x sinx 2.下列结论中正确的是 ，,,,,,,,,,,,,,,,,,, 【 A.导数为零的点一定是极值点B. 如果在X o 附近的左侧f'(x) 0，右侧f'(x) ::: 0，那么f (X o )是极大值C. 如果在X 。

附近的左侧f '(x)，右侧f'(x) :: 0，那么f(Xo )是极小值D. 如果在x 0附近的左侧f'(x) ：：：0,右侧f'(x)・0，那么f(x 0)是极大值3兀3. 曲线y=cosx(0—X "，与坐标轴围成的面积是，，，，，”，,”2【 】5A.4B.C.3D.2234. 函数 f(x) =3x-4x , [0,1]的最大值是，”,，，，，，，，，，，，，【1A.1B.C.0D.-1[25.如果10N 的力能使弹簧压缩10cm ，为在弹性限度内将弹簧从平衡位置拉到离平衡位置 6cm 处，则克服弹力所做的功为 ，,,,,,,,,,,,,,,,,,,,,，【A . 0.28JB. 0.12JC. 0.26JD. 0.18J6.给出以下命题: b⑴若 f (x)dx 0，则 f(x)>0 ；asin xdx 二4 ；⑶f(x)的原函数为F(x)，且F(x)是以aT 为周期的函数，则.f (x)dx-a TT f(x)dx ；其中正确命题的个数为,A. 1B. 2C. 3D. 0 7.若函数f (X) x 2 mx 1 是 R 上的单调函数，则实数 m 的取值范围是A. 】1 (-+oc ) (3，)1 B.(一：弓 8.设 0< a <b ，且 1亠 1亠x f (X) = 1——」，则下列大小关系式成立的是9.函数f(x) =ax3 4-b 在区间(v ,0)内是减函数，贝U a,b 应满足”,”，”,【 】A. a ::: 0且 b = 0且b R10. f (x)与g(x)是R 定义在上的两个可导函数，若f(x)与g(x)满 足八))))))))))))))))))))))))))))))))))【】A. f(X)二 g(x)B. f(x)-g(x)为常数函数c. f (x)二g(x) =0D. f(x) g(x)为常数函数211. (2007江苏)已知二次函数f (x) = ax bx c 的导数为f (x)， f (0) 0 ,对于任意实数x，有f(x > ),则f (1 昇 的丿 最小值0 )为丿 7 )))))))))))))))))))))))))【】53A. 3B.c. 2D.2212. (2007江西理)设函数f (x)是R 上以 5为周期的可导偶函数，则曲线 y = f(x)在 x =5处的切线的斜率为( )11A.--B. 0c.—D .555二、填空题(共4小题，每小题5分，共20分)13. 10.曲线y=2x 3— 3x 2共有 _____ 个极值.16.已知函数f (x) = x3ax 2 bx c 在x = -2处取得极值，并且它的图象与直线2y= _3x ' 3在点(1, 0)处相切，则函数 f (x)的表达式为 _____________ ____ __ m.314.已知 f (x)为一次函数，且 _______________ f (x) =x +2J ° f(t)dt ，贝U f (x) =a +bI —A.f(a )< f ()<f( ab )2— a ■ bC. f ( ..ab )< f ()<f (a )a + brB. f ()<f (b)< f (. ab )2a + b[~~c. a ■ 0 且 b = 0 D . a ■ 0f (x)与g (x)满足 f (x) = g (x)，则 15.若 f (x) = ef (1 -2t) -f(1)三、解答题(共74分)17.(本小题满分10分)一物体沿直线以速度v(t) = 2t-3 (t的单位为秒,v的单位为：米/秒)的速度作变速直线运动，求该物体从时刻t=0秒至时刻t=5秒间运动的路程？18.(本小题满分12分)已知曲线y = x3+ x—2在点P o处的切线11平行直线4x—y—仁0 ,且点P o在第三象限，⑴求P o的坐标；⑵若直线I _ h ,且I也过切点P o ,求直线l的方程.3 219.(本小题满分12分)已知函数f(x)二ax (a -1)x 48(^ 2)x b的图象关于原点成中心对称，试判断f(x)在区间1-4,4上的单调性，并证明你的结论•120.(本小题满分14 分)已知函数f(x)=l nx (x 式0),函数g(x)=—；—+ af"(x)(x^0) f(x)⑴当x = 0时，求函数y = g(x)的表达式；⑵若a 0,函数y=g(x)在(0,=)上的最小值是2 ,求a的值;27y x 与函数y = g(x)的图象所围成图形的面积⑶在⑵的条件下，求直线3 621. (本小题满分 12 分)设 a > 0 , f(x)=x_1_ln 2x 2alnx(x .O).(I)令F(x)二xf (x)，讨论F(x)在(0,^)内的单调性并求极值； (H)求证：当 x 1 时，恒有 x .In 2x_2alnx J .22. (本小题满分14分)已知函数 f(x)=e x-kx, x R(I)若k 二e ,试确定函数f (x)的单调区间；(n)若k 0，且对于任意R , f(x) 0恒成立，试确定实数 k 的取值范围；n(川)设函数 F(x) = f(x) f(-x)，求证：F(1)F(2)|||F(n) (e n12円n N ).3、将半径为R 的球加热，若球的半径增加 R ，则球体积的平均变化率为(2 ^4 3^4A 4 兀 R 2"A R +4兀 R +_ 兀(A R )B 、 4 兀 R 2+4兀 R 边R +_ 兀33数学科学段测试(导数部分)一、选择题(12小题，共36分)1、 设曲线y = x 2A (0,- 2)2、 抛物线y=x?在点M (— 2 B 、45°A 30° •x -2在点M 处切线斜率为3,则点M 的坐标为B 、( 1,1、4C 0) C 、(0, 0)D 的切线的倾斜角是 ()、(1,1) (、60° D 、90° 3“R )2C4. R 2R D 、4. R 24、 函数y=x 3— 3x 在［—1, 2］上的最小值为 （）A 2B 、一 2C 、0D — 45、 设函数f x 的导函数为f x ，且f x = x 22x f 1 ,则f 0等于（）A 0B 、_4C 、_2D 、26已知曲线y 」x 3在点P （2,8），则过P 点的切线方程为（）3 3 A 、3x -12y _16 二 0 B 、12x-3y -16=0 C 、 3x-12y 16 = 0 D 12x_3y16=07、 已知f （x ） = x 3+ ax 2+ （a + 6）x + 1有极大值和极小值，则a 的取值范围为（）A 、— 1<a<2B 、— 3<a<6C 、a<— 1 或 a>2D 、a<— 3 或 a>68、 设函数f （x ）在定义域内可导，y=f （x ）的图象如下图所示，贝U 导函数 y=f0） 可能为 （）值范围是1 1A 、kB 0 ：：： k _ —3 310、 函数y=xlnx 的单调递减区间是A 、（ e 4，+x ）B 、（ — X ，e 4） 11、 方程x 3— 6x 2+9x — 10=0的实根个数是A . 3B . 2C . 112、对于R 上可导的任意函数f （x ），且f '（1） = 0若满足（x — 1） f（ x ）>0,则 必有（）A f (0) + f (2) ：(1)B 、f (0) + f ⑵ -2f (1)C 、f (0) + f (2) >2f (1) D、f (0) + f (2) -2f (1)二、填空题（4小题，共16分）13、【文】已知函数y=x 3-3x ，则它的单调递增区间是 _________________13、【理】 计算定积分： 2（x sinx ）dx = _________________14、 已知函数y =lnsinx 和y 二a 2x 的导函数分别是 ___________ 、 ____________ < 15、 【文】一质点在直线上从时刻t=0秒以速度v （t ）二t 2-4t • 3 （米/秒）运动,则该质点在时刻t=3秒时运动的路程为 ___________________ 。

曲边梯形面积与定积分一、选择题1.给出如下命题：①错误！超链接引用无效。

(错误！超链接引用无效。

为常数且错误!超链接引用无效。

)；②错误！超链接引用无效.；③曲线错误！超链接引用无效。

,错误！超链接引用无效。

错误!超链接引用无效.，与直线错误!超链接引用无效.围成的两个封闭区域的面积之和为错误！超链接引用无效。

其中真命题的错误!超链接引用无效.个数为（）Ａ.错误！超链接引用无效。

Ｂ。

错误！超链接引用无效。

Ｃ。

错误!超链接引用无效。

Ｄ.错误!超链接引用无效.答案:Ｂ2.错误!超链接引用无效。

等于()Ａ。

错误！超链接引用无效。

Ｂ.错误！超链接引用无效。

Ｃ.错误！超链接引用无效。

Ｄ。

错误！超链接引用无效。

答案：Ｃ3。

若某产品一天内的产量是时间错误！超链接引用无效。

的函数，若已知产量的变化率为错误!超链接引用无效。

，那么从第3小时到第6小时期间内的产量为（）Ａ.错误！超链接引用无效。

Ｂ。

错误！超链接引用无效.Ｃ.错误！超链接引用无效。

Ｄ.错误！超链接引用无效。

答案：Ｄ4.错误！超链接引用无效。

,则错误！超链接引用无效。

的最大值是(）Ａ.错误!超链接引用无效。

Ｂ.错误！超链接引用无效。

Ｃ.错误！超链接引用无效.Ｄ。

错误！超链接引用无效。

答案：Ｂ二错误!超链接引用无效.、填空题错误！超链接引用无效。

5.若错误!超链接引用无效。

是一次函数,且错误！超链接引用无效。

,错误！超链接引用无效.,那么错误！超链接引用无效。

的值是。

答案:错误！超链接引用无效.6。

物体按照规律错误！超链接引用无效。

错误！超链接引用无效。

做直线运动,设介质的阻力与速度成正比,且速度等错误！超链接引用无效.于错误！超链接引用无效。

时,阻力为错误！超链接引用无效.,则物体从错误!超链接引用无效。

到错误!超链接引用无效。

阻力所做的功等于.答案:错误！超链接引用无效。

三、解答题7。

在曲线错误!超链接引用无效。

上某一点错误！超链接引用无效.处作一切线使之与曲线以及错误！超链接引用无效。

《曲边梯形的面积定积分》练习题一、选择题1．将和式的极限)0(.......321lim1>+++++∞→p n n P pp p p n 表示成定积分（ ）A ．dx x ⎰101B ．dx x p ⎰1C ．dx x p ⎰10)1(D ．dx n x p⎰10)(2．下列等于1的积分是 （ ）A ．dx x ⎰1B ．dx x ⎰+1)1(C ．dx ⎰101D ．dx ⎰10213．曲线]23,0[,cos π∈=x x y 与坐标周围成的面积（ ） A ．4B ．2C ．25D ．34．dx e e x x ⎰-+1)(=（ ）A ．ee 1+B ．2eC ．e2D ．ee 1-5． 若()f x 是[,]a a -上的连续偶函数，则 ()d aaf x x -=⎰（ ）A ．0()d a f x x -⎰B ．0C ．02()d a f x x -⎰D ．0()d af x x ⎰6． 1321(tan sin )x x x x dx -++⎰=（ ）A ．0B..13202(tan sin )x x x x dx ++⎰C ．03212(tan sin )x x x x dx -++⎰D..13202|tan sin |x x x x dx ++⎰7、已知f (x )为偶函数且60⎰f (x )d x ＝8，则66-⎰f (x )d x 等于 ( )A ．0B ．4C ．8D ．16 8．设连续函数f(x)>0,则当a<b 时，定积分()d b af x x ⎰的符号（ ）A ．一定是正的B ．一定是负的C ．当0<a<b 时为正，当a<b<0时为负D ．以上结论都不正确9．求由1,2,===y x e y x 围成的曲边梯形的面积时，若选择ｘ为积分变量，则积分区间为（ ） A ．［0，2e ］ B ．［0，2］ C ．［1，2］ D ．［0，1］ 10．由直线1,+-==x y x y ，及ｘ轴所围成平面图形的面积为（）A ．()[]dy y y ⎰--11B.()[]dx x x ⎰-+-2101C ．()[]dy y y ⎰--2101D.()[]dx x x ⎰+--10111． 若()f x 与()g x 是[,]a b 上的两条光滑曲线，则由这两条曲线及直线x =a , x =b 所围图形的面积（ ）A ．()()d ba f x g x x -⎰B ．(()())d baf xg x x -⎰C ．(()())d b ag x f x x -⎰ D ．(()())d baf xg x x -⎰12. 如图所示，在一个边长为1的正方形AOBC 内，曲线2y x y x ==和曲线围成一个叶形图（阴影部分），向正方形AOBC 内随机投一点（该点落在正方形AOBC 内任何一点是等可能的），则所投的点落在叶形图内部的概率是 （ ） A ．13 B ．23 C ．14 D ．34二、填空题1、给出下列定积分：①20sin xdx π⎰ ②02sin xdx π-⎰ ③23xdx -⎰ ④231x dx -⎰其中为负值的有 2、给出下列命题： ①若()ba f x dx ⎰＞0，b ＞a ，则f(x)＞0；②若f(x)＞0，b ＞a ，则()baf x dx ⎰＞0；③若()baf x dx ⎰=0，b ＞a ，则f(x)=0；④若f(x)=0，b ＞a ，则()baf x dx ⎰=0；⑤若|()|baf x dx ⎰=0，b ＞a ，则f(x)=0。

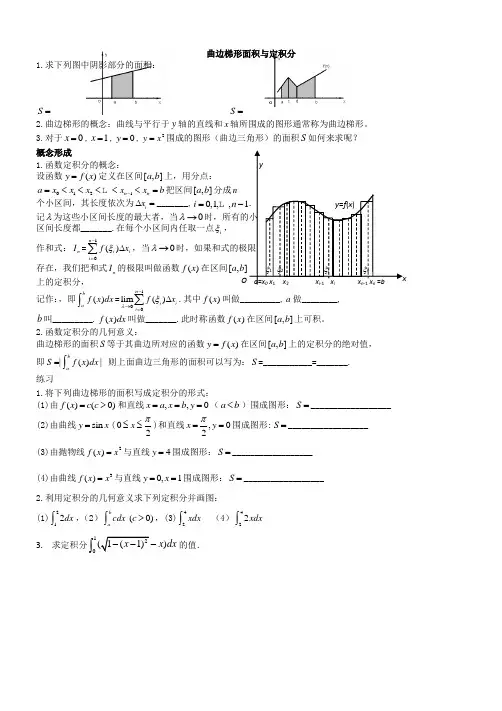
a =x 0 x 1 x 2 x i -1 x i x n -1 x n =b ξiO ξn ξ1 ξ2 y =f (x )x y曲边梯形面积与定积分1.求下列图中阴影部分的面积：___________________S = ___________________S =2.曲边梯形的概念：曲线与平行于y 轴的直线和x 轴所围成的图形通常称为曲边梯形。

3.对于0x =,1x =,0y =,2y x =围成的图形（曲边三角形）的面积S 如何来求呢？ 概念形成1.函数定积分的概念：设函数()y f x =定义在区间[,]a b 上，用分点： 0121n n a x x x x x b -=<<<<<= 把区间[,]a b 分成n个小区间，其长度依次为i x ∆=_______,0,1,,1i n =- .记λ为这些小区间长度的最大者，当0λ→时，所有的小区间长度都_______.在每个小区间内任取一点i ξ，作和式：n I =10()n i i i f x ξ-=∆∑，当0λ→时，如果和式的极限存在，我们把和式n I 的极限叫做函数()f x 在区间[,]a b 上的定积分，记作：，即()b a f x dx ⎰=100lim ()n i i i f x λξ-→=∆∑.其中()f x 叫做_________,a 做________, b 叫_________.()f x dx 叫做_______.此时称函数()f x 在区间[,]a b 上可积。

2.函数定积分的几何意义：曲边梯形的面积S 等于其曲边所对应的函数()y f x =在区间[,]a b 上的定积分的绝对值， 即|()|ba S f x dx =⎰ 则上面曲边三角形的面积可以写为：S =___________=_______. 练习1.将下列曲边梯形的面积写成定积分的形式：(1)由()(0)f x c c =>和直线,,0x a x b y ===（a b <）围成图形：S =__________________(2)由曲线sin y x =(02x π≤≤)和直线,02x y π==围成图形:S =__________________(3)由抛物线2()f x x =与直线4y =围成图形：S =__________________(4)由曲线3()f x x =与直线0,1y x ==围成图形：S =__________________2.利用定积分的几何意义求下列定积分并画图：(1)212dx ⎰，（2）b a cdx ⎰(0)c >，(3)42xdx ⎰ （4）422xdx ⎰ 3. 求定积分120(1(1))x x dx ---⎰的值．。

22、定积分22．1 曲边梯形地面积与定积分【知识网络】1．了解定积分地实际背景.2．初步了解定积分地概念，并能根据定积分地意义计算简单地定积分.【典型例题】[例1]<1）已知和式当n→+∞时，无限趋近于一个常数A，则A可用定积分表示为<）A．B．C．D．<2）下列定积分为1是<）A．B．C．D．<3）求由围成地曲边梯形地面积时，若选择ｘ为积分变量，则积分区间为<）A．［0，］B．［0，2］C．［1，2］D．［0，1］<4）由y=cosx 及x 轴围成地介于0与2π之间地平面图形地面积，利用定积分应表达为． <5）计算=.[例2]①利用定积分地几何意义，判断下列定积分地值是正是负？ <1）； <2）； <3）．②利用定积分地几何意义，比较下列定积分地大小．，，.[例3]计算下列定积分：；；；. [例4] 利用定积分表示图中四个图形地面积：A ．B.C.D. 2． =<） A ．0B.(1> (2>(3>(4>C． D.3．设连续函数f(x>＞0，则当a＜b时，定积分地符号<）A．一定是正地B．当0<a<b时为正，当a<b<0时为负C．一定是负地D．当0<a<b时为负，当a<b<0时为正4．由直线，及ｘ轴所围成平面图形地面积为<）A． B.C． D.5．和式当n→+∞时，无限趋近于一个常数A，则A用定积分可表示为.6．曲线，所围成地图形地面积可用定积分表示为．7．计算曲边三角形地面积地过程大致为：分割；以直代曲；作和；逼近.试用该方法计算由直线x=0，x=1，y=0和曲线y=x2所围成地曲边三角形地面积.<下列公式可供使用：12+22+…+n2=）8．求由曲线与所围地图形地面积.9．计算，其中,10．弹簧在拉伸过程中，力与伸长量成正比，即力F(x>=kx<k是正地常数，x是伸长量），求弹簧从平衡位置拉长b所做地功.22、定积分22．1 曲边梯形地面积与定积分A组若是上地连续偶函数，则1．）<A．B．0C．D．2．变速直线运动地物体地速度为v(t>，初始t=0时所在位置为，则当秒末它所在地位置为< ）A．B．C．D．3．由直线，及ｘ轴所围成平面图形地面积为<）A．B．C．D．4．设且，，给出下列结论：①A＞0；②B＞0；③；④.其中所有正确地结论有.5．设函数f (x>地图象与直线x =a, x =b及x轴所围成图形地面积称为函数f(x>在[a，b]上地面积.已知函数y＝sinnx在[0，]<n∈N*）上地面积为.①y＝sin3x在[0,]上地面积为；②y＝sin<3x－π）＋1在[，]上地面积为.6．求由曲线与所围地图形地面积.7．试根据定积分地定义说明下列两个事实：①；②.8．物体按规律<m）作直线运动，设介质地阻力与速度成正比，且速度等于10<m/s）时阻力为2<N），求物体从x=0到x=2阻力所做地功地积分表达式．22、定积分22．1 曲边梯形地面积与定积分B组1．如果1kg力能拉长弹簧1cm，为了将弹簧拉长6cm，则力所作地功为）<A．0.18kg·m D．0.28kg·mC．0.12kg·mB．0.26kg·m2．<已知b＞a，下列值：，，||地大小关系为）A．||≥≥B.≥||≥C．= ||=D．= ||≥3．若与是上地两条光滑曲线，则由这两条曲线及直线x=a, x=b所围图形地面积<）A．B．C．D．4．给出下列命题：①若＞0，b＞a，则f(x>＞0；②若f(x>＞0，b＞a，则＞0；③若=0，b＞a，则f(x>=0；④若f(x>=0，b＞a，则=0；⑤若=0，b＞a，则f(x>=0.其中所有正确命题地序号为.5．给出下列定积分：①②③④其中为负值地有.6．求由曲线所围图形地面积. 7．计算：.8．试问下面地结论是否成立？若函数f(x>在区间[a，b]上是单调增函数，则.若成立，请证明之；若不成立，请说明理由.参考答案22．1 曲边梯形地面积与定积分【典型例题】[例1]<1）B．<2）C．B.3．<4）或.<5）.提示：这是求单位圆落在第一象限内部分地面积. [例2]①<1）正 (2>正 (3>负.②≥≥.[例3](1>； (2>；(3>0 ；(4>0.[例4](1>；(2>；(3>；(4>．【课内练习】C.1．2．A.提示：被积函数为奇函数，且积分区间又关于原点对称，利用定积分地几何意义知，面积地代数和为0.3． A.4． C.5．.6．.7．.提示：请参看教材P42~44.8． 6.9． 6.10．可用“分割；以直代曲；作和；逼近”求得：.22．1 曲边梯形地面积与定积分A组C.1．B.2．3．C.①③④.4．①；②.5．6．.7．定积分地定义实质反映了计算地过程，也就是：分割；以直代曲；作和；逼近.可尝试用这四步进行说明或证明.8．变力作功公式中，F(x>是用x表示地，而此题中只有x对t地关系式，故首先将F表示出来．依题意得：F＝kv，但这不是x地函数，应将v用x表示．∵v=x＇=8t，而，∴．另外，此题F是与物体运动方向相反地，∴．B组A.1．B.2．A.3．②④⑤.4．②③.5．.6．2π.提示：问题即求上半圆地面积.7．结论成立.说明可按照定积分地定义进行.8．个人收集整理-仅供参考申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途.11 / 11。

曲边梯形面积与定积分得分一、选择题(共12小题，每小题5分,共60分）1、函数y=x2co sx的导数为…………………………………………………………………【】A、y′=2x co sx－x2s i nxB、y′=2x co sx+x2s i nxC、y′=x2co sx－2xs i nxD、y′=x co sx－x2s i nx2、下列结论中正确的是……………………………………………………………………【】A、导数为零的点一定是极值点…………………………………………………………【】B、如果在错误！超链接引用无效.附近的左侧错误！超链接引用无效。

，右侧错误！超链接引用无效。

，那么错误！超链接引用无效。

是极大值C、如果在错误！超链接引用无效.附近的左侧错误！超链接引用无效.,右侧错误!超链接引用无效。

,那么错误！超链接引用无效.是极小值D、如果在错误!超链接引用无效。

附近的左侧错误！超链接引用无效。

，右侧错误!超链接引用无效。

，那么错误！超链接引用无效。

是极大值3、曲线错误！超链接引用无效。

与坐标轴围成的面积是…………………………………【】A、4B、错误！超链接引用无效。

C、3D、24、函数错误!超链接引用无效.,错误!超链接引用无效.的最大值是…………………………………………【】A、1B、错误！超链接引用无效。

C、0 错误！超链接引用无效。

D、-15、如果10N的力能使弹簧压缩10cm，为在弹性限度内将弹簧从平衡位置拉到离平衡位置6cm处,则克服弹力所做的功为…………………………………………………………【】A 、0、28J B、0、12J C、0、26J D、0、18J6、给出以下命题:⑴若错误！超链接引用无效。

，则f(x)>0; ⑵错误!超链接引用无效。

;⑶f （x)的原函数为F(x）,且F（x）是以T为周期的函数，则错误！超链接引用无效。

；其中正确命题的个数为…【】A、1B、2C、3D、07、若函数错误！超链接引用无效.是R上的单调函数，则实数m的取值范围是………【】A、错误!超链接引用无效。

1.5 定积分1.5.1 曲边梯形的面积 1.5.2 定积分5分钟训练 （预习类训练，可用于课前）1.在求由x=a,x=b(a<b),y=f(x)［f(x)≥0］及y=0围成的曲边梯形的面积S 时，在区间［a,b ］上等间隔地插入n-1个分点，分别过这些分点作x 轴的垂线，把曲边形分成n 个小曲边形，下列说法中正确的个数是…（ ） ①n 个小曲边形的面积和等于S ②n 个小曲边形的面积和小于S ③n 个小曲边形的面积和大于S④n 个小曲边形的面积和与S 之间的大小关系无法确定A.1B.2C.3D.4 答案：A解析:根据“化整为零”“积零为整”的思想，知①是正确的. 2.函数f(x)=x 2在区间［n i 1-,ni］上,则（ ） A.f(x)的值变化很小 B.f(x)的值变化很大C.f(x)的值不变化D.当n 很大时，f(x)的值变化很小 答案：D解析:因为分割得越细，越接近原函数值，所以当n 很大时，f(x)的值变化很小. 3.定积分的性质 (1)⎰ba kf (x)dx=____________⎰bax f )(dx.(2)⎰±ba x fx f )]()([21dx=⎰baf 1(x)dx____________.(3)⎰bax f )(dx=⎰cax f )(dx+____________(a<c<b).答案：(1)k· (2)±⎰baf 2(x)dx(3)⎰bax f )(dx10分钟训练 （强化类训练，可用于课中）1.设函数f(x)在区间［a,b ］上连续，用分点a=x 0<x 1<…<x i-1<x i <…<x n =b ，把区间［a,b ］等分成n 个小区间，在每个小区间［x i-1,x i ］上任取一点ξi (i=1,2,…,n)，作和式I n =∑=ni if 1)(ξΔx(其中Δx 为小区间的长度)那么I n 的大小（ ）A.与f(x)和区间［a,b ］有关，与分点的个数n 和ξi 的取法无关B.与f(x)、区间［a,b ］和分点个数n 有关，与ξi 的取法无关C.与f(x)、区间［a,b ］和ξi 的取法有关，与分点的个数n 无关D.与f(x)、区间［a,b ］、分点的个数n 、ξi 的取法都有关 答案：D解析:根据定积分的定义可知n 越大即分点越多，与f(x)的值越接近，与ξi 的取法也有关.2.⎰1dx ∫10dx 等于（ ）A.0B.1C.21D.2 答案：B 解析:⎰1dx =x 10,故⎰1dx =1.3.下列等式成立的是（ ） A.⎰baxdx 0=b-a B.⎰baxdx =21C.⎰-11||x dx=2⎰10||x dx D.⎰+bax )1(dx=⎰b axdx答案：C解析:根据定积分的定义可知⎰-11||x dx=2⎰1||x dx.4.当n 很大时，函数f(x)=x 2在区间［n i 1-,ni］上的值，可以用____________近似代替（ ） A.f(n 1) B.f(n 2) C.f(ni) D.f(0)答案：C 5.定积分⎰bax f )(dx 的大小（ ）A.与f(x)和积分区间［a,b ］有关，与ξi 的取法无关B.与f(x)有关，与区间［a,b ］以及ξi 的取法无关C.与f(x)以及ξi 的取法有关，与区间［a,b ］无关D.与f(x)、区间［a,b ］和ξi 的取法都有关 答案：A 6.证明⎰+b a x g x f )]()([dx=⎰bax f )(dx+⎰bax f )(dx.证明:⎰+b ax g x f )]()([dx=nab g f ni i i -+∑=1)]()([ξξ =∞→n lim∑=-+ni i i nab g f 1)]()([ξξ =])()([lim 11∑∑==∞→-+-n i i ni i n n a b g n a b f ξξ=∑∑==∞→∞→-+-n i i ni n i n n a b g n a b f 11)(lim )(limξξ=⎰bax f )(dx+⎰bax g )(dx.30分钟训练 （巩固类训练，可用于课后） 1.下列结论中成立的个数是（ ）①⎰103x dx=∑=ni n i 133·n 1 ②⎰103x dx=∑=∞→-n i m n i 13)1(lim ·n 1 ③⎰103x dx=∞→m lim ∑=ni n i 13)(·n 1A.0B.1C.2D.3答案：C2.下列等式成立的个数是（ ） ①⎰bax f )(dx=∑=ni f 1(ξi )n a b - ②⎰b a x f )(dx=∞→m lim f(ξi )nab - ③⎰b a x f )(dx=∞→m lim∑=ni f1(ξi )nab - A.0 B.1 C.2 D.3 答案：B 3.已知⎰bax f )(dx=6,则⎰bax f )(6dx 等于（ ）A.6B.6（b-a ）C.36D.不确定 答案：C 4.已知⎰31)(x f dx=56,则（ ）A.⎰21)(x f dx=28 B.⎰32)(x f dx=28C.⎰21)(2x f dx=56 D.⎰21)(x f dx+∫32f(x)dx=56答案：D 5.计算⎰1031x 2dx.解:⎰1031x 2dx=⎰10231x dx=∑=∞→ni n n i 12)(lim 31·n 1=36)12)(1(lim 31nn n n n ++∞→=91. 6.求抛物线y=x 2与直线x=0,x=1,y=0所围成的平面图形的面积S. 解:（1）分割在区间［0，1］上等间隔地插入n-1个点，将它等分成n 个小区间：［0，n 1］,［n 1,n2］,…, ［nn 1-,1］, 记第i 个区间为［n i 1-,n i ］(i=1,2,…,n),其长度为Δx=n i n i 1--=n1. 分别过上述n-1个分点作x 轴的垂线，把曲边梯形分成n 个小曲边梯形，它们的面积记作：ΔS 1,ΔS 2,…,ΔS n .S=∑=∆ni iS1.(2)近似代替记f(x)=x 2.当n 很大，即Δx 很小时，在区间［n i 1-,ni］上，可以认为f （x ）=x 2的值变化很小，近似地等于一个常数，不妨认为它近似地等于左端点n i 1-处的函数值f(ni 1-)，就是用平行于x 轴的直线段近似地代替小曲边梯形的曲边.这样，在区间［n i 1-,ni］上，用小矩形的面积ΔS i ′近似地代替ΔS i ，即在局部小范围内“以直代曲”，则有 ΔS i ≈ΔS i ′=f(n i 1-)Δx=(ni 1-)2·Δx =(n i 1-)2·n1(i=1,2,…,n).① （3）求和 由①，得S n =∑=∆n i iS 1'=∑=ni f 1(n i 1-)Δx=∑=-ni n i 12)1(·n 1 =［0·n 1+(n 1)2·n 1+…+(n n 1-)2·n1］ =31n［12+22+…+（n-1）2］ =6)12()1(13--n n n n =31(1n 1-)(1n21-). 从而得到S 的近似值 S≈S n =31(1n 1-)(1n21-). (4)取极限分别将区间［0，1］等分成8，16，20,…等份，可以看到，随着n 的不断增大，即Δx 越来越小时，S n =31(1n 1-)·(1n21-)越来越趋向于S,从而有 S=∞→n lim S n =∞→n lim∑=ni n 11f(n i 1-) =∞→n lim31(1n 1-)(1n 21-)=31. 7.某物体做变速直线运动，设该物体在时刻t 的速度为v(t)=7-t 2,试计算这个物体在0≤t≤1这段时间内运动的路程s.解:s=∞→n lim ∑=ni v 1(n i 1-)Δt=∞→n limn n i ni 1)]1(7[1∑=--=∞→n lim ［76)12()1(13---n n n n ］=731-=320. 8.利用定积分的定义，计算⎰10xdx 的值.解：(1)分割：在区间［0，1］上等间隔地插入n-1个分点，把区间［0，1］等分成n 个小区间［n i 1-,ni］(i=1,2,…,n),每个小区间的长度为Δx=x i -x i-1=n i -n i 1-=n1.(2)近似代替、求和： 取ξi =ni(i=1,2,…,n),则 ⎰1xdx ≈S n=∑=ni f 1(n i)·Δx=∑=ni n i 1·n1 =∑=ni i n121=1i=21n·2)1(+n n =n n 21+. (3)取极限：⎰1xdx =∞→n lim S n =∞→n limn n 21+=21.。

1.4.1 曲边梯形面积与定积分课后训练1．当n 很大时，函数f (x )＝x 2在区间1,i i n n -⎡⎤⎢⎥⎣⎦上的值，可以用下列中的哪一项来近似代替( )．A ．1()f n B ．2()f n C ．()if n D ．f (0)2．下列等式成立的是( )．A ．ba ⎰0d x ＝b －aB ．1d 2b a x x =⎰C ．11-⎰|x |d x ＝210⎰|x |d xD ．ba ⎰(x ＋1)d x ＝b a ⎰x d x3．由曲线y ＝x 2－1，直线x ＝0，x ＝2和x 轴围成的封闭图形(如图)的面积是()．A ．20⎰(x 2－1)d xB ．2201d x x (-)⎰C ．20⎰|x 2－1|d xD ．11-⎰(x 2－1)d x ＋21⎰(x 2－1)d x4．用定积分表示下列阴影部分的面积(不要求计算)：(1)S 1＝__________(图①)；(2)S 2＝__________(图②)；(3)S 3＝__________(图③)．5．不用计算，根据图形，用大于、小于号连接下列各式：(1)10⎰x d x ________10⎰x 2d x (图①)； (2)10⎰x d x ________21⎰x d x (图②)．6．若π20⎰cos x d x ＝1，则由x ＝0，x ＝π，f (x )＝sin x 及x 轴围成的图形的面积为________．7．利用定积分的几何意义计算20⎰(2x ＋1)d x . 8．利用定义计算定积分10⎰(x 2＋2)d x .参考答案1.答案：C 任一函数在1,i in n-⎡⎤⎢⎥⎣⎦上的值均可以用ifn⎛⎫⎪⎝⎭近似代替．2.答案：C3.答案：C4.答案：(1)ππ3⎰sin x d x(2)2241d2x x-⎰(3)1924()dx x--⎰5.答案：(1)＞(2)＜6.答案：2 由正弦函数与余弦函数的图象，知f(x)＝sin x，x[0，π]的图象与x轴围成的图形的面积等于g(x)＝cos x，xπ0,2⎡⎤⎢⎥⎣⎦的图象与x轴围成的图形的面积的2倍．所以答案应为2.7.答案：分析：通过数形结合思想求曲边形的面积，相当于求f(x)在区间[a，b]上的定积分(或定积分的绝对值)．解：如图，所求定积分为阴影部分的面积，且面积为12×(1＋5)×2＝6 ∴2⎰(2x＋1)d x＝6.8.答案：分析：按照由定义求定积分的步骤求解即可．解：把区间[0,1]分成n等份，分点和小区间的长度分别为x i＝in(i＝1，2，…，n－1)，Δx i＝1n(i＝1,2，…，n)，取ξi＝in(i＝1,2，…，n)，作积分和()1ni iif xξ=∆∑＝21(2)ni iixξ=∆∑＋＝2112niin n=⎡⎤⎛⎫+⋅⎢⎥⎪⎝⎭⎢⎥⎣⎦∑＝1023112iin=+∑＝3116n⋅n(n＋1)(2n＋1)＋2＝11112+26n n⎛⎫⎛⎫++⎪⎪⎝⎭⎝⎭.∵λ＝1n，当λ→0时，n→＋∞，∴1⎰(x2＋2)d x＝()limni inif xξ→∞=∆∑＝limn→∞11112+26n n⎡⎤⎛⎫⎛⎫++⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦＝13＋2＝73.。