一阶谓词逻辑word版本
- 格式:ppt
- 大小:136.50 KB
- 文档页数:38





一阶谓词逻辑部分——一阶语法:1定义字母表的定义一个一阶语言L的字母表由以下符号组成:1)一组非逻辑符号,其中包含:i)一个(可能空的)个体常项集;{a1,a2,…}ii)对每个n ≥1, 一个(可能空的)n元谓词集;{F11,F12,…,F21,F22,…,F n1,F n2,…,…}iii)对每个n ≥1, 一个(可能空的)n元函数符号集{f11,f12,…,f21,f22,…,f n1,f n2,…,…}2)一组固定的逻辑符号,其中包含:i)个体变项x0, x1, x2,…(可数无穷多);ii)量词∀,[∃];iii)联结词⌝,→,[∧,∨,↔];iv)等词[≡];v)括号),(。
注1:我们上面定义的,可以叫做带等词的一阶语言的字母表。
形式语言对其字母集(及其每个子类)的大小做了限定,要求它(它们)是可数的。
这是因为,对不可数集合,一般没有一个能行的方法来判定一个对象是否属于它。
注2:所有一阶语言有共同的逻辑符号,它们的字母表的差别完全由非逻辑符号决定,所以,在不引起误解的情况下,我们不妨把一个一阶语言就简单地看成它的非逻辑符号集。
注3:一个语言(的字母表)虽然可能是为了描述某个特殊的结构而设计的,但字母表一旦给定,这个语言也可以用来描述其他的结构,只要这些结构的组成与这些字母(的一部分)相匹配就行。
注4:在谈论一个一阶语言的时候,我们需要一些元语言的变项来代表这个(对象)语言字母表中的任意某类符号。
我们约定,在元语言中用x, y, z等代表一阶语言的个体变项;c, d, e等代表一阶语言的个体常项;P, Q, R等代表一阶语言的谓词;f, g, h等代表一阶语言的函数符号。
2 项的归纳定义下一步我们要从字母表中构造一阶语言的词项(以下简称项)。
项的作用是指称或表示结构中的个体,所以个体常项是一种项,个体变项是另一种项,而函数,如f(x) = x的母亲,其函数值也代表个体,所以函数表达式也是项。




知识表⽰之⼀阶谓词逻辑表⽰⾸先引⼊知识概念:知识(Knowledge)是⼈们在改造客观世界的实践中形成的对客观事物(包括⾃然的和⼈造的)及其规律的认识,包括对事物的现象、本质、状态、关系、联系和运动等的认识。
知识是把有关的信息关联在⼀起,形成的关于客观世界某种规律性认识的动态信息结构。
知识=事实+规则+概念:事实就是指⼈类对客观世界、客观事物的状态、属性、特征的描述,以及对事物之间关系的描述;规则是指能表达在前提和结论之间的因果关系的⼀种形式;概念主要指事实的含义、规则、语义、说明等。
所谓知识表⽰(Knowledge Representation),就是把知识⽤计算机可接受的符号并以某种形式描述出来。
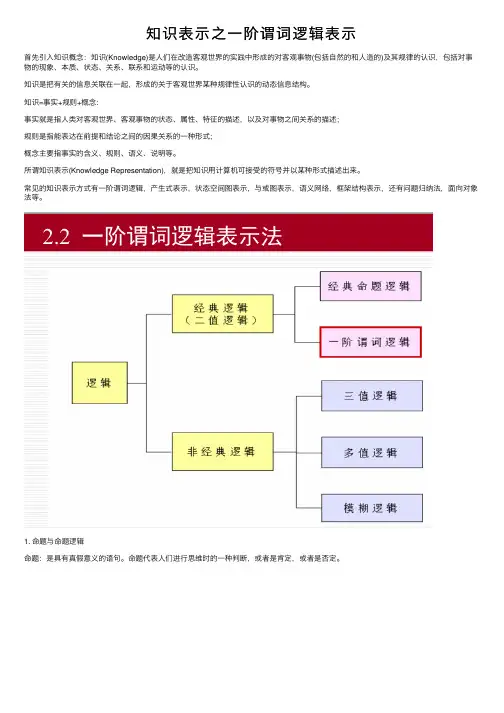
常见的知识表⽰⽅式有⼀阶谓词逻辑,产⽣式表⽰,状态空间图表⽰,与或图表⽰,语义⽹络,框架结构表⽰,还有问题归纳法,⾯向对象法等。
1. 命题与命题逻辑命题:是具有真假意义的语句。
命题代表⼈们进⾏思维时的⼀种判断,或者是肯定,或者是否定。
命题逻辑:“命题逻辑”是“谓词逻辑”的基础。
在现实世界中,有些陈述语句在特定情况下都具有“真”或“假”的含义,在逻辑上称这些语句为“命题”。
如:A. 天在下⾬ B. 天晴 C. ⽇照的天⽓很宜⼈ D. 我们在⾟苦于远程研修中。
表达单⼀意义的命题称为“原⼦命题”。
命题逻辑就是研究命题和命题之间关系的符号逻辑系统。
命题逻辑的联结词:原⼦命题可通过“联结词”构成“复合命题”,联结词有5种,定义为:﹁表⽰否定,复合命题“﹁Q”即“﹁Q”∧表⽰合取,复合命题“P∧Q”表⽰“P与Q”∨表⽰析取,复合命题“P∨Q”表⽰“P或Q”→表⽰条件(蕴含),复合命题“P→Q”表⽰“如果P,那么Q”↔表⽰双条件(等价),复合命题“P↔Q”即表⽰“P当且仅当Q”2. 谓词与谓词逻辑谓词逻辑是命题逻辑的扩充和发展,它将⼀个原⼦命题分解成个体和谓词两个组成部分。
在谓词公式 P(x) 中,P 称为谓词,x 称为个体变元,若 x 是⼀元的,称为⼀元谓词, P(x,y) 称为⼆元谓词。
第二章 一阶谓词逻辑一阶谓词逻辑在计算机科学中有着广泛的应用,它不仅是程序设计理论、程序逻辑研究的重要基础,而且还是程序正确性证明、定理机器证明和知识表示技术的有力工具。
一阶谓词逻辑和命题逻辑也是研究其它逻辑系统的内核和基础,其它逻辑系统都可看作是它们的扩充和推广。
在命题逻辑中原子命题是研究问题的基本概念,原子命题是构筑命题逻辑的基本单位。
原子命题具有怎样的内部结构或逻辑形式我们并未分析。
其实,讨论一类各命题之间的逻辑关系并不简单地体现在原子命题之间而往往体现在构成原子命题的内部成分之间,体现在命题结构更深的层次之上。
从后文的一个例子我们将看到,尽管在命题逻辑中研究了命题间的有效推理,但是一些常见的推理却不能得到表达。
运用命题逻辑的知识,我们能完成下述推理: 若厂方拒绝增加工资(P),则罢工不会停止(¬Q),除非罢工超过一年(S)且工厂经理辞职(R)。
如果厂方拒绝增加工资而罢工又持续不久(S),问在这种情况下罢工能否停止(Q ?Q ?)。
¬¬ H 1:(P ∧(S ∧R))→¬¬QH 2:PH 3:S¬ C : Q ?Q ?¬ 形式方法论证:G 1:S ¬P 规则,引入H 3G 2:R ∨S ¬¬T 规则,对G 1附加G 3:(R ∧S) ¬T 规则,对G 2反演G 4:P P 规则,引入H 2 - 65 -¬T规则,对G4,G3合成G5:P∧(R∧S)¬¬Q P规则,引入H1G6:(P∧(R∧S))→¬T规则,对G5,G6假言推理G7:Q但在命题逻辑中我们无法完成下述推理:凡人皆有死(P),苏格拉底是人(Q),所以苏格拉底有死(R)。
H1:PH2:QC:R?如果P,Q⇒R,那末P∧Q→R是重言式,但P∧Q→R不是重言式,所以P,Q R。
/⇒这说明了什么呢?命题(有真假意义之一的陈述句)作为论证的基础,只能构筑人们思维论证的一个方面。