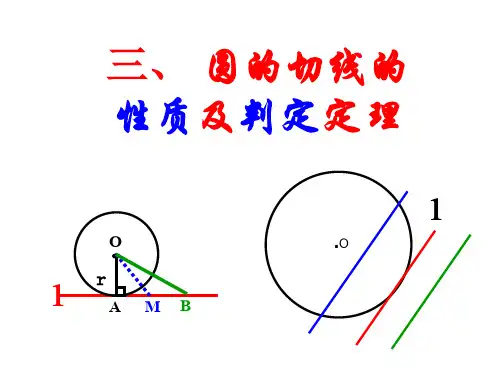
切线的定义和判定定理

即B一定点在圆外．由点B的任意性可知，圆与直线 只有一个公共点，因此l 是圆的切线．由此可得：
切线的判定定理：
经过半径的外端并且垂直于这 条半径的直线是圆的切线．
O
l
AB
例1 如图,AB是⊙O的直径, ⊙O过BC的中点D, DE⊥AC.求证:DE是⊙O是切线.
证明:连接OD.
∵BD=CD,OA=OB, ∴OD是△ABC的中位线,
D C
A
O
B
P322
思考:切线的性质定理逆命题“经过半径的外端并且 垂直于这条半径的直线是圆的切线．”是否成立?
已知：点A是⊙O与直线l 的公共点,且 l ⊥OA .
求证：圆与直线只有一个公共点 证明：在l 上任取异于点A的点B,则△OAB是Rt△
而OB是Rt△ OAB的斜边，因此，都有OB>OA,
C P321
∴OD//AC.
又∵∠DEC=90º ∴∠ODE=90º 又∵D在圆周上,
∴DE是⊙O是切线..E D NhomakorabeaB
A
O
三、 圆的切线的 性质及判定定理
O
r
l A MB
l
.O
1 切线的性质定理：圆的切线垂直于经过切点的半径．
l
AM
反证法
假设不垂直, 作OM⊥l
因“垂线段最 故OA>OM,
O
即短圆”心, 到直线距离小于半径.
这与线圆相切矛盾.
因为经过一点只有一条直线与已知直线垂直，所 以经过圆心垂直于切线的直线一定过切点；反之,过切 点且垂直于切线的直线也一定过圆心.由此得到：
推论1: 经过圆心且垂直于切线的直线必经过切点.
推论2: 经过切点且垂直于切线的直线必经过圆心.

切线证明法切线的性质定理： 圆的切线垂直于经过切点的半径切线的性质定理的推论１: 经过圆心且垂直于切线的直线必经过切点． 切线的性质定理的推论２: 经过切点且垂直于切线的直线必经过圆心 切线的判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线．切线长定理: 从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。

一、要证明某直线是圆的切线，如果已知直线过圆上的某一个点，那么作出过这一点的半径，证明直线垂直于半径．【例1】如图1，已知AB 为⊙O 的直径，点D 在AB 的延长线上，BD ＝OB ,点C 在圆上，∠CAB ＝30º．求证:DC 是⊙O 的切线．思路:要想证明DC 是⊙O 的切线，只要我们连接OC ，证明∠OCD ＝90º即可． 证明：连接OC ，BC ．∵AB 为⊙O 的直径，∴∠ACB ＝90º．∵∠CAB ＝30º，∴BC ＝21AB ＝OB ．∵BD ＝OB ，∴BC ＝21OD ．∴∠OCD ＝90º．∴DC 是⊙O 的切线．【评析】一定要分清圆的切线的判定定理的条件与结论，特别要注意“经过半径的外端”和“垂直于这条半径”这两个条件缺一不可，否则就不是圆的切线．【例2】如图2，已知AB 为⊙O 的直径,过点B 作⊙O 的切线BC ,连接OC ,弦AD ∥OC ．求证：CD 是⊙O 的切线．思路：本题中既有圆的切线是已知条件，又证明另一条直线是圆的切线．也就是既要注意运用圆的切线的性质定理，又要运用圆的切线的判定定理．欲证明CD 是⊙O 的切线，只要证明∠ODC ＝90º即可．图1图2证明：连接OD ．∵OC ∥AD ，∴∠1＝∠3，∠2＝∠4． ∵OA ＝OD ，∴∠1＝∠2．∴∠3＝∠4． 又∵OB ＝OD ，OC ＝OC ，∴△OBC ≌△ODC ．∴∠OBC ＝∠ODC ．∵BC 是⊙O 的切线，∴∠OBC ＝90º．∴∠ODC ＝90º． ∴DC 是⊙O 的切线．【例3】如图2,已知AB 为⊙O 的直径,C 为⊙O 上一点，AD 和过C 点的切线互相垂直，垂足为D ．求证:AC 平分∠DAB ．思路：利用圆的切线的性质--与圆的切线垂直于过切点的半径．证明：连接OC ．∵CD 是⊙O 的切线，∴OC ⊥CD ．∵AD ⊥CD ，∴OC ∥AD ．∴∠1＝∠2． ∵OC ＝OA ，∴∠1＝∠3．∴∠2＝∠3． ∴AC 平分∠DAB ．【评析】已知一条直线是某圆的切线时,切线的位置一般是确定的．在解决有关圆的切线问题时，辅助线常常是连接圆心与切点，得到半径，那么半径垂直切线．【例4】 如图1,B 、C 是⊙O 上的点，线段AB 经过圆心O ，连接AC 、BC ，过点C 作CD ⊥AB 于D ,∠ACD =2∠B ．AC 是⊙O 的切线吗？为什么？解：AC 是⊙O 的切线． 理由：连接OC , ∵OC =OB ， ∴∠OCB =∠B ．图3 OABCD2 31∵∠COD是△BOC的外角,∴∠COD=∠OCB+∠B=2∠B．∵∠ACD=2∠B，∴∠ACD=∠COD．∵CD⊥AB于D,∴∠DCO+∠COD=90°．∴∠DCO+∠ACD=90°．即OC⊥AC．∵C为⊙O上的点，∴AC是⊙O的切线．【例5】如图2,已知⊙Ｏ是△ABC的外接圆，AB是⊙Ｏ的直径,D是AB的延长线上的一点，AE⊥DC交DC的延长线于点E，且AC平分∠EAB．求证：DE是⊙O的切线．证明:连接OC,则OA=OC，∴∠CAO=∠ACO，∵AC平分∠EAB，∴∠EAC=∠CAO=∠ACＯ,∴AE∥CO,又AE⊥DE，∴CO⊥DE，∴DE是⊙O的切线．二、直线与圆的公共点未知时须通过圆心作已知直线的垂直线段，证明此垂线段的长等于半径【例6】如图3，AB=AC，OB=OC，⊙O与AB边相切于点D．证明：连接OD，作OE⊥AC，垂足为E．∵AB=AC，OB=OC．∴AO为∠BAC角平分线，∠DAO=∠EAO∵⊙O与AB相切于点D，∴∠BDO=∠CEO=90°．∵AO=AO∴△ADO≌△AEO，所以OE=OD．∵OD是⊙O的半径,∴OE是⊙O的半径．∴⊙O与AC边相切．【例7】如图,在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于E，B为切点的切线交OD延长线于F.求证：EF与⊙O相切.证明：连结OE,AD。

切线与过切点的半径所在的直 线相互垂直。
02
切线的判定方法
利用定义判定切线
总结词：直接验证
详细描述：根据切线的定义，如果直线与圆只有一个公共点，则该直线为圆的切 线。因此，可以通过验证直线与圆的交点数量来判断是否为切线。
利用切线的性质判定切线
总结词：半径垂直
详细描述：切线与过切点的半径垂直，因此，如果已知过切点的半径，可以通过验证直线与半径的夹角是否为直角来判断是 否为切线。
切线判定定理的变种
切线判定定理的变种
除了标准的切线判定定理，还存在一些变种，如利用切线的 性质来判断是否为切线，或者利用已知点和切线的性质来判 断未知点是否在曲线上。
切线判定定理的应用
切线判定定理在几何证明题中有着广泛的应用，如证明某直 线为圆的切线，或者判断某点是否在曲线上。这些应用都需 要熟练掌握切线判定定理及其变种。
04
切线判定定理的证明
定理的证明过程
第一步
根据题目已知条件，画 出图形，标出已知点和
未知点。
第二步
根据切线的定义，连接 已知点和未知点，并作
出过这两点的割线。
第三步
根据切线和割线的性质 ，证明割线与圆只有一 个交点，即证明割线是
圆的切线。
第四步
根据切线的判定定理， 如果一条割线满足上述 性质，则这条割线是圆
切线判定定理在其他领域的应用
物理学中的应用
在物理学中，切线判定定理可以应用于研究曲线运动和力的分析。例如，在分析物体在曲线轨道上的 运动时，可以利用切线判定定理来判断物体的运动轨迹是否与轨道相切。
工程学中的应用
在工程学中，切线判定定理可以应用于机械设计和流体力学等领域。例如，在机械设计中，可以利用 切线判定定理来判断曲轴是否与轴承相切，从而避免轴承的损坏。在流体力学中，可以利用切线判定 定理来判断流体是否沿着流线流动。

切线长定理—知识讲解（基础）责编：康红梅【学习目标】1.了解切线长定义；理解切线的判定和性质；理解三角形的内切圆及内心的定义；2.掌握切线长定理；利用切线长定理解决相关的计算和证明.【要点梳理】要点一、切线的判定定理和性质定理1．切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线.要点诠释：切线的判定方法：（1）定义：直线和圆有唯一公共点时，这条直线就是圆的切线；（2）定理：和圆心的距离等于半径的直线是圆的切线；（3）判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线.（切线的判定定理中强调两点：一是直线与圆有一个交点，二是直线与过交点的半径垂直，缺一不可）.2．切线的性质定理：圆的切线垂直于过切点的半径.要点诠释：切线的性质：（1）切线和圆只有一个公共点；（2）切线和圆心的距离等于圆的半径；（3）切线垂直于过切点的半径；（4）经过圆心垂直于切线的直线必过切点；（5）经过切点垂直于切线的直线必过圆心.要点二、切线长定理1．切线长：经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长.要点诠释：切线长是指圆外一点和切点之间的线段的长，不是“切线的长”的简称.切线是直线，而非线段.2．切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.要点诠释：切线长定理包含两个结论：线段相等和角相等.3．圆外切四边形的性质：圆外切四边形的两组对边之和相等.要点三、三角形的内切圆1．三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆.2．三角形的内心：三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心.要点诠释：(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形；(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即(S 为三角形的面积，P 为三角形的周长，r 为内切圆的半径).【典型例题】 类型一、切线长定理1．如图，PA 、PB 、DE 分别切⊙O 于A 、B 、C ，⊙O 的半径长为6 cm ，PO ＝10 cm ，求△PDE 的周长．【答案与解析】连结OA ，则OA ⊥AP ． 在Rt △POA 中，PA ＝22OA OP -＝22610-＝8（cm ）．由切线长定理，得EA ＝EC ，CD ＝BD ，PA ＝PB ，∴ △PDE 的周长为PE ＋DE ＋PD ＝PE ＋EC ＋DC ＋PD ，＝PE ＋EA ＋PD ＋DB＝PA ＋PB ＝16（cm ）．【总结升华】本题考查切线长定理、切线的性质、勾股定理．注意：在有关圆的切线长的计算中，往往利用切线长定理进行线段的转换．【高清ID号：356967 关联的位置名称（播放点名称）：方法总结及例题1-2】2．（2015•柳州）如图，已知四边形ABCD是平行四边形，AD与△ABC的外接圆⊙O恰好相切于点A，∠DAE=∠ABE,边CD与⊙O相交于点E，连接AE，BE．（1）求证：AB=AC；（2）若过点A作AH⊥BE于H，求证：BH=CE+EH．【思路点拨】（1）根据圆周角定理证明∠ABC=∠ACB，得到答案；（2）作AF⊥CD于F，证明△AEH≌△AEF，得到EH=EF，根据△ABH≌△ACF，得到答案．【答案与解析】证明：（1）∵∠ABE=∠DAE，又∠EAC=∠EBC，∴∠DAC=∠ABC，∵AD∥BC，∴∠DAC=∠ACB，∴∠ABC=∠ACB，∴AB=AC；（2）作AF⊥CD于F，∵四边形ABCE是圆内接四边形，∴∠ABC=∠AEF，又∠ABC=∠ACB，∴∠AEF=∠ACB，又∠AEB=∠ACB，∴∠AEH=∠AEF，在△AEH和△AEF中，，∴△AEH≌△AEF，∴EH=EF，∴CE+EH=CF，在△ABH和△ACF中，，∴△ABH≌△ACF，∴BH=CF=CE+EH．【总结升华】本题考查的是切线的性质和平行四边形的性质以及全等三角形的判定和性质，运用性质证明相关的三角形全等是解题的关键，注意圆周角定理和圆内接四边形的性质的运用．举一反三：【变式】（2015•青海）如图，在△ABC中，∠B=60°，⊙O是△ABC的外接圆，过点A作⊙O的切线，交CO的延长线于点M，CM交⊙O于点D．（1）求证：AM=AC；（2）若AC=3，求MC的长．【答案】（1）证明：连接OA，∵AM是⊙O的切线，∴∠OAM=90°，∵∠B=60°，∴∠AOC=120°，∵OA=OC，∴∠OCA=∠OAC=30°，∴∠AOM=60°，∴∠M=30°，∴∠OCA=∠M，∴AM=AC；（2）作AG⊥CM于G，∵∠OCA=30°，AC=3，∴AG=，由勾股定理的，CG=，则MC=2CG=3．类型二、三角形的内切圆3．已知：如图，△ABC的三边BC=a，CA=b，AB=c，它的内切圆O的半径长为r．求△ABC 的面积S．【答案与解析】设内切圆与三角形的三边AB 、AC 、BC 分别交于D 、E 、F ，连接OE 、 OF 、OD 、AO 、BO 、CO.∴△ABC=△AO B +△AO C +△BO C=12r(a+b+c). 【总结升华】考虑把△ABC 的面积分割成3个以圆的半径为高的三角形面积的和，从而求出△ABC 的面积.举一反三：【高清ID 号：356967 关联的位置名称（播放点名称）：切线长定理及例3】【变式】已知如图，△ABC 中，∠C=90°，BC=4，AC=3，求△ABC 的内切圆⊙O 的半径r.【答案】连结OA 、OB 、OC ，∵△ABC 中，∠C=90°，BC=4，AC=3，∴AB=5.则S △AOB +S △COB +S △AOC =S △ABC ，即11115+4+3=34=12222r r r r ⨯⨯⨯⨯⨯，类型三、与相切有关的计算与证明4．（2016•自贡）如图，⊙O 是△ABC 的外接圆，AC 为直径，弦BD=BA ，BE ⊥DC 交DC 的延长线于点E ．（1）求证：∠1=∠BAD ；（2）求证：BE 是⊙O 的切线．【思路点拨】（1）根据等腰三角形的性质和圆周角定理得出即可；（2）连接BO ，求出OB ∥DE ，推出EB ⊥OB ，根据切线的判定得出即可；【答案与解析】证明：（1）∵BD=BA ，∴∠BDA=∠BAD ，∵∠1=∠BDA ，∴∠1=∠BAD ；（2）连接BO ，∵∠ABC=90°，又∵∠BAD +∠BCD=180°，∴∠BCO +∠BCD=180°，∵OB=OC ，∴∠BCO=∠CBO ，∴∠CBO+∠BCD=180°，∴OB∥DE，∵BE⊥DE，∴EB⊥OB，∵OB是⊙O的半径，∴BE是⊙O的切线．【总结升华】本题考查了三角形的外接圆与外心，等腰三角形的性质，切线的判定，熟练掌握切线的判定定理是解题的关键．。

2、已知：如图：AB是⊙O的弦， AC 切 ⊙ 于 点 A ， 且 ∠ BAC=54° ， 求∠OBA的度数。
例1、求证：经过直径的两端点的圆的切
线互相平行。
已知：如图，AB是圆
A
C
O的直径，直线
AC,BD分别是过点A,B
O
的圆O的切线。
求证 : AC BD
证明：如图，
D
B
∵AC、BD是⊙O的切线 AB 是⊙O的直径
求证：ＡＣ平分∠ＤＡＢ
D
C
A
B
O
变式训练（１） 已知ＡＢ是⊙Ｏ的直径， ＡＣ平分∠ＤＡＢ，ＤＣ与⊙Ｏ切于的 点Ｃ，求证：ＡＤ⊥ＣＤ
D C
A
பைடு நூலகம்
B
O
• 变式训练（２）如图，ＡＢ是⊙Ｏ的 直径，，ＣＤ与⊙Ｏ切于点Ｃ，ＡＤ ⊥ＣＤ于Ｄ，ＢＣ、ＡＤ的延长线交 于点Ｅ，且ＡＥ＝ＢＥ，求∠Ａ的度 数。
E
D
c
A
B
切线的性质定理
1.圆的切线垂直于经过切点的半径
2.经过圆心且垂直于切线的直线必经过切点 3.经过切点且垂直于切线的直线必经过圆心
1、按图填空：(口答) (1). 如果AB切⊙O于A， 那么 OA⊥ AB.
(2). 如果半径OA⊥AB， 那么AB是 ⊙O的切线
B A
O
(3).如果AB是⊙O的切线，OA⊥AB，那么A是 切点
求∠ABD的度数.
C
B
解：∵ AB为直径
∴∠ABC=90°
BC为切线
∠ADB=90°
∵ △ABC为直角三角形 AD=DC
∴△ABD为等腰直角三角形
∴AD=DB ∠ADC=90°
∴∠ABD=45°

小试牛刀
例2：如图，已知：AB=AC，点O在AB上，⊙O过点B，分别与边BC、AB交于D、E两点，过D点作DF⊥AC于F， （1）求证：DF是⊙O的切线；
证明：连结OD， ∵OB=OD，∴∠ODB=∠B 又∵AB=AC，∴∠C=∠B ∴∠ODB=∠C ∴OD∥AC 又∵DF⊥AC ∴∠DFC=90° ∴∠ODF=∠DFC=90° ∴DF⊥OD ∴DF为⊙O的切线
注意：确定唯一公共点，可证明直线和圆相切
例1：直线l和⊙O的公共点的个数为m，且m满足方程 m2+2m- 3=0, 试判断直线l和⊙ O的位置关系，并 说明理由.
例3．如图，直线y=－ x+4与y轴交于点A，与x轴交于 点B，以点C（ ，0）为圆心，OC的长为半径作⊙C， 证明：AB是⊙C的切线。 M 分析：由于不知AB和⊙C是否有公共点，故考虑过C作CM⊥AB于M，再证CM为⊙C的半径即可
小结一
确定唯一公共点，证切线
无交点，作垂直，证半径
有交点，连半径，证垂直
证明切线的一般方法简单表述为：
小试牛刀
例3：如图，已知：AB=AC，点O在AB上，⊙O过点B，分别与边BC、AB交于D、E两点，过D点作DF⊥AC于F，
（2）连结OP ∵AC与⊙O相切于点P，∴OP⊥AC 由（1）可知OD∥AC，且DF⊥AC， 故四边形ODFP为正方形 ∴PF=OD=OB=3 设AC=x，则在Rt△APO中有 AP2+OP2=OA2 即(x－4)2+32=(x－3)2 解得x=8 ∴AC=8
是圆的切线
是圆的切线
是圆的切线
3、圆的切线性质定理：圆的切线垂直于经过切点的半径。 辅助线作法：连接圆心与切点可得半径与切线垂直。 即“连半径，得垂直”。

切线的判定和性质
切线的性质与判定
1.主要性质
（1）切线和圆只有一个公共点；
（2）切线和圆心的距离等于圆的半径；
（3）切线垂直于经过切点的半径；
（4）经过圆心垂直于切线的直线必过切点；
（5）经过切点垂直于切线的直线必过圆心；
（6）从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

其中（1）是由切线的定义得到的，（2）是由直线和圆的位置关系定理得到的，（6）是由相似三角形推得的，也就是切割线定理。

2.判定
切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。

圆的切线垂直于这个圆过切点的半径。

（打印3份）圆----切线的性质和判定（11月12）A、知识点、方法归纳总结知能点1：切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。

切线的识别方法有三种：（1）和圆只有一个公共点的直线是圆的切线。

（2）和圆心的距离等于圆的半径的直线是圆的切线。

（3）切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线辅助线的作法：证明一条直线是圆的切线的常用方法：当直线和圆有一个公共点时，把圆心和这个公共点连接起来,则得到半径，然后证明直线垂直于这条半径，记为“连半径，证垂直。

”知能点2：切线的性质定理：圆的切线垂直于过切点的半径。

辅助线的作法：有圆的切线时，常常连接圆心和切点得切线垂直半径。

记为“见切线，连半径，得垂直。

”中考考点点击：切线的判定和性质在中考中是重点内容，试题题型灵活多样，填空、选择、作图、解答题较多。

B、证明圆的切线方法及例题一、若直线l过⊙O上某一点A，证明l是⊙O的切线，只需连OA，证明OA⊥l就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直.例1 如图，在△ABC 中，AB=AC ，以AB 为直径的⊙O 交BC 于D ，交AC 于E ，B 为切点的切线交OD 延长线于F.求证：EF 与⊙O 相切. 证明：连结OE ，AD. ∵AB 是⊙O 的直径， ∴AD ⊥BC. 又∵AB=BC ， ∴∠3=∠4.∴BD=DE，∠1=∠2. 又∵OB=OE ，OF=OF ， ∴△BOF ≌△EOF （SAS ）. ∴∠OBF=∠OEF. ∵BF 与⊙O 相切， ∴OB ⊥BF. ∴∠OEF=900. ∴EF 与⊙O 相切.说明：此题是通过证明三角形全等证明垂直的例2 如图，AD 是∠BAC 的平分线，P 为BC 延长线上一点，且PA=PD.求证：PA 与⊙O 相切. 证明一：作直径AE ，连结EC. ∵AD 是∠BAC 的平分线，∴∠DAB=∠DAC. ∵PA=PD ， ∴∠2=∠1+∠DAC. ∵∠2=∠B+∠DAB ， ∴∠1=∠B. 又∵∠B=∠E ， ∴∠1=∠E∵AE 是⊙O 的直径， ∴AC ⊥EC ，∠E+∠EAC=900. ∴∠1+∠EAC=900.⌒ ⌒即OA ⊥PA.∴PA 与⊙O 相切.说明：此题是通过证明两角互余，证明垂直的，解题中要注意知识的综合运用. 变式练习： 如图，AB=AC ，AB 是⊙O 的直径，⊙O 交BC 于D ，DM ⊥AC 于M 求证：DM 与⊙O 相切.例3 如图，已知：AB 是⊙O 的直径，点C 在⊙O 上，且∠CAB=300，BD=OB ，D 在AB 的延长线上.求证：DC 是⊙O 的切线 证明：连结OC 、BC. ∵OA=OC ， ∴∠A=∠1=∠300. ∴∠BOC=∠A+∠1=600. 又∵OC=OB ，∴△OBC 是等边三角形. ∴∠CBO=600. OB=BC. ∵OB=BD ， ∴BC=BD.∴∠CDO=300∴∠OCD=180°-300-600=900. ∴OC ⊥CD.∴DC 是⊙O 的切线.变式练习：如图，ABCD是正方形，G是BC延长线上一点，AG交BD于E，交CD于F.求证：CE与△CFG的外接圆相切.二、若直线l与⊙O没有已知的公共点，又要证明l是⊙O的切线，只需作OA⊥l，A为垂足，证明OA是⊙O的半径就行了，简称：“作垂直；证半径”例4 如图，AB=AC，D为BC中点，⊙D与AB切于E点.求证：AC与⊙D相切.证明一：连结DE，作DF⊥AC，F是垂足.∵AB是⊙D的切线，∴DE⊥AB.∵DF⊥AC，∴∠DEB=∠DFC=900.∵AB=AC，∴∠B=∠C.又∵BD=CD，∴△BDE≌△CDF（AAS）∴DF=DE.∴F在⊙D上.∴AC是⊙D的切线变式练习： 已知：如图，AC ，BD 与⊙O 切于A 、B ，且AC ∥BD ，若∠COD=900. 求证：CD 是⊙O 的切线.C 、作业部分1、如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于D ，且CO=CD ，则∠PCA=（ ）A ．30° B ．45° C ．60° D ．67.5°2、O ，并使较长边与O 相切于点C .假设角尺的较长边足够长，角尺的顶点B ，较短边8cm AB .若读得BC 长为cm a ，则用含a 的代数式表示r 为 .3、如图，已知AB 是⊙O 的一条直径，延长AB 至C 点，使得AC=3BC ，CD 与⊙O 相切，切点为D.若CD=3，则线段BC 的长度等于__________.4、如图，已知AB是⊙O的直径，锐角∠DAB的平分线AC交⊙O于点C，作CD⊥AD，垂足为D，直线CD与AB的延长线交于点E．（1）求证：直线CD为⊙O的切线；（2）当AB＝2BE，且CE＝3时，求AD的长．5如图，在Rt△ABC中，∠C=90°，O、D分别为AB、BC上的点．经过A、D两点的⊙O分别交AB、AC于点E、F，且D为弧EF的中点．求证：BC与⊙O相切；6、如图，已知AB 是⊙O 的直径，C 是AB 延长线上一点，BC ＝OB ，CE 是⊙O 的切线，切点为D ，过点A 作AE ⊥CE ，垂足为E ，求CD ：DE 的值7、如图，AB 是半圆O 的直径，点C 是⊙O 上一点（不与A ，B 重合），连接AC ，BC ，过点O 作OD ∥AC 交BC 于点D ，在OD 的延长线上取一点E ，连接EB ，使∠OEB=∠ABC ． ⑴求证：BE 是⊙O 的切线；⑵若OA=10，BC=16，求BE 的长．EB8、如图，⊙ O经过点B、D、E，BD是⊙ O的直径，∠C＝90°，BE 平分∠ABC. (1)试说明直线AC是⊙ O的切线；(2)当AE＝4，AD＝2时，求⊙ O的半径及BC的长．9、如图，在⊙O中，AB为直径，AC为弦，过点C作CD⊥AB 与点D，将△ACD沿AC翻折，点D落在点E处，AE交⊙O于点F ,连接OC、(1）求证：CE是⊙O的切线。

切线长定理—知识讲解（提高）责编：康红梅【学习目标】1.了解切线长定义；理解切线的判定和性质；理解三角形的内切圆及内心的定义；2.掌握切线长定理；利用切线长定理解决相关的计算和证明.【要点梳理】要点一、切线的判定定理和性质定理1．切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线.要点诠释：切线的判定方法：（1）定义：直线和圆有唯一公共点时，这条直线就是圆的切线；（2）定理：和圆心的距离等于半径的直线是圆的切线；（3）判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线.（切线的判定定理中强调两点：一是直线与圆有一个交点，二是直线与过交点的半径垂直，缺一不可）.2．切线的性质定理：圆的切线垂直于过切点的半径.要点诠释：切线的性质：（1）切线和圆只有一个公共点；（2）切线和圆心的距离等于圆的半径；（3）切线垂直于过切点的半径；（4）经过圆心垂直于切线的直线必过切点；（5）经过切点垂直于切线的直线必过圆心.要点二、切线长定理1．切线长：经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长.要点诠释：切线长是指圆外一点和切点之间的线段的长，不是“切线的长”的简称.切线是直线，而非线段.2．切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.要点诠释：切线长定理包含两个结论：线段相等和角相等.3．圆外切四边形的性质：圆外切四边形的两组对边之和相等.要点三、三角形的内切圆1．三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆.2．三角形的内心：三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心. 要点诠释：(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形； (2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即(S 为三角形的面积，P 为三角形的周长，r 为内切圆的半径).(3) 三角形的外心与内心的区别：名称 确定方法 图形性质外心(三角形外接圆的圆心)三角形三边中垂线的交点(1)OA=OB=OC ；(2)外心不一定在三角形内部内心(三角形内切圆的圆心)三角形三条角平分线的交点(1)到三角形三边距离相等；(2)OA 、OB 、OC 分别平分 ∠BAC 、∠ABC 、∠ACB ； (3)内心在三角形内部.【典型例题】类型一、切线长定理1. 如图，等腰三角形ABC 中，6AC BC ==，8AB =．以BC 为直径作⊙O 交AB 于点D ，交AC 于点G ，DF AC ⊥，垂足为F ，交CB 的延长线于点E ．求证：直线EF 是⊙O 的切线.DFGCO B E A【答案与解析】如图，连结OD 、CD ，则90BDC ∠=︒．∴CD AB ⊥． ∵ AC BC =，∴AD BD =． ∴D 是AB 的中点． ∵O 是BC 的中点， ∴DO AC ∥． ∵EF AC ⊥于F ． ∴EF DO ⊥．∴EF 是⊙O 的切线． 【总结升华】连半径，证垂直.举一反三：【变式】已知：如图，在梯形 ABCD中，AB∥DC，∠B=90°，AD=AB+DC，AD是⊙O的直径．求证：BC和⊙O相切．【答案】作OE⊥BC，垂足为E，∵ AB∥DC，∠B=90°，∴ OE∥AB∥DC，∵ OA=OD，∴ EB=EC，∴ BC是⊙O的切线．2.已知：如图，AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于弦AD，求证：DC是⊙O的切线．【答案与解析】连接OD．∵ OA=OD，∴∠1=∠2．∵ AD∥OC，∴∠1=∠3，∠2=∠4．因此∠3=∠4．又∵ OB=OD，OC=OC，∴△OBC≌△ODC．∴∠OBC=∠ODC．∵BC是⊙O的切线，∴∠OBC=90°，∴∠ODC=90°，∴ DC是⊙O的切线．【总结升华】因为AB是直径，BC切⊙O于B，所以BC⊥AB．要证明DC是⊙O的切线，而DC和⊙O 有公共点D，所以可连接OD，只要证明DC⊥OD．也就是只要证明∠ODC=∠OBC.而这两个角分别是△ODC和△OBC的内角，所以只要证△ODC≌△OBC．这是不难证明的．举一反三：【高清ID号：356967 关联的位置名称（播放点名称）：练习题精讲】【变式】已知：∠MAN=30°，O为边AN上一点，以O为圆心、2为半径作⊙O，交AN于D、E两点，设AD=x，⑴如图⑴当x取何值时，⊙O与AM相切；⑵如图⑵当x为何值时，⊙O与AM相交于B、C两点，且∠BOC=90°．【答案】（1）设AM与⊙O相切于点B，并连接OB，则OB⊥AB；在△AOB中，∠A=30°，则AO=2OB=4，所以AD=AO-OD，即AD=2．x=AD=2.（2）过O点作OG⊥AM于G∵OB=OC=2，∠BOC=90°，∴BC=222，2∴OA=22∴x=AD=22 2类型二、三角形的内切圆3.（2015•西青区二模）已知四边形ABCD中，AB∥CD，⊙O为内切圆，E为切点．（Ⅰ）如图1，求∠AOD的度数；（Ⅱ）如图1，若AO=8cm，DO=6cm，求AD、OE的长；（Ⅲ）如图2，若F是AD的中点，在（Ⅱ）中条件下，求FO的长．【答案与解析】解：（Ⅰ）∵⊙O为四边形ABCD的内切圆，∴AD、AB、CD为⊙O的切线，∴OD平分∠ADC，OA平分∠BAD，即∠ODA=∠ADC，∠OAD=∠BAC，∵AB∥CD，∴∠ADC+∠BAC=180°，∴∠ODA+∠OAD=90°，∴∠AOD=90°；（Ⅱ）在Rt△AOD中，∵AO=8cm，DO=6cm，∴AD==10（cm），∵AD切⊙O于E，∴OE⊥AD，∴OE•AD=OD•OA，∴OE==（cm）；（Ⅲ）∵F是AD的中点，∴FO=AD=×10=5（cm）．【总结升华】本题考查了三角形的内切圆与内心，也考查了切线长定理．类型三、与相切有关的计算与证明4.（2016•三明）如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB 于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．（1）判断直线DE与⊙O的位置关系，并说明理由；（2）若AC=6，BC=8，OA=2，求线段DE的长．【思路点拨】（1）直线DE与圆O相切，理由如下：连接OD，由OD=OA，利用等边对等角得到一对角相等，等量代换得到∠ODE为直角，即可得证；（2）连接OE，设DE=x，则EB=ED=x，CE=8﹣x，在直角三角形OCE中，利用勾股定理列出关于x的方程，求出方程的得到x的值，即可确定出DE的长．【答案与解析】解：（1）直线DE与⊙O相切，理由如下：连接OD，∵OD=OA，∴∠A=∠ODA，∵EF是BD的垂直平分线，∴EB=ED，∴∠B=∠EDB，∵∠C=90°，∴∠A+∠B=90°，∴∠ODA+∠EDB=90°，∴∠ODE=180°﹣90°=90°，∴直线DE与⊙O相切；（2）连接OE，设DE=x，则EB=ED=x，CE=8﹣x，∵∠C=∠ODE=90°，∴OC2+CE2=OE2=OD2+DE2，∴42+（8﹣x）2=22+x2，解得：x=4.75，则DE=4.75．【总结升华】此题考查了直线与圆的位置关系，以及线段垂直平分线定理，熟练掌握直线与圆相切的性质是解本题的关键．。

O l A
切线必须同时满足两条：①经过半径 外端；②垂直于这条半径．
如图，如果直线l是⊙O的切线，切点为A， 那么半径OA与直线l是不是一定垂直呢？
∵ l是⊙O的切线，切点为A
O
l A
∴ l ⊥OA
切线的性质定理：圆的
切线垂直于过切点的半径。
数学语言：
O l A
∵ l是⊙O的切线，切点为A
∴ l ⊥OA
A P
C B
O
如图，已知：在△ABC中，∠B＝90°，O是AB上一 点，以O为圆心，OB为半径的圆交AB于点E，切AC 与点D。求证：DE∥OC
C 证明：连接ＢＤ． ∵∠ＡＢＣ＝９０°，ＯＢ为⊙Ｏ的半径 ∴ＣＢ是⊙Ｏ的切线 ∵ＡC是⊙Ｏ的切线，Ｄ是切点 ∴ＣＤ＝ＣＢ，∠１＝∠２ ∴ＯＣ⊥ＢＤ ∵ＢＥ是⊙Ｏ的直径 ∴∠ＢＤＥ＝９０°，即ＤＥ⊥ＢＤ ∴ＤＥ∥ＯＣ A E D O
勾股（逆）定理 切 线 判 定
∴C(-2,0), P(0,-4) 数据“放入”图中。猜想直线 又∵ D(0,1) OC=2, OP=4 ,OD=1, DP=5 PC 与⊙ D∴ 相切。怎么证？联 又∵在Rt△COD中, CD2=OC2+OD2=4+1=5 想证明切线的两种方法。点 在Rt△COP中, CP2=OC2+OP2=4+16=20 C 在圆上，即证：∠ DCP=90° 在△ CPD中, CD2+CP2=5+20=25, DP2=25 2 2 2 ∴ CD +CP =DP 利用勾股及逆定理可得。
即：△CDP为直角三角形,且∠DCP=90° ∴PC为⊙D的切线.
已知,如图,D(0,1),⊙D交y轴于A、B两点,交x轴负 半轴于C点,过C点的直线:y=－2x－4与y轴交于P. ⑵判断在直线PC上是否存在点E，使得S△EOC= 4S△CDO,若存在，求出点E的坐标；若不存在， 请说明理由.

圆的切线的判定定理的证明
1．圆的切线的判定定理的证明
【知识点的知识】
1、直线和圆的位置关系：
相交：直线与圆有两个公共点时，叫做直线和圆相交，这时直线叫做圆的割线．
相切：直线和圆有唯一公共点时，叫做直线和圆相切，这时直线叫做圆的切线，唯一的公共点叫做切点．相离：直线和圆没有公共点时，叫做直线和圆相离．
2、切线的性质定理：圆的切线垂直于过切点的直径（或半径）．
3、由直线与圆的位置关系和切线的性质定理推理总结出切线的判定定理：
切线的判定定理：经过半径（或直径）的外端并且垂直于这条半径（直径）的直线是圆的切线．
注意：“经过半径（或直径）的外端”和“垂直于这条半径（或直径）”这两个条件缺一不可．
4、切线的判定方法：
①直线到圆心的距离等于该圆的半径（直线与圆的位置关系）；
②线与圆有唯一公共点（切线定义）；
③切线的判定定理．
1/ 1。

直线和圆的位置关系判定方法
直线和圆的位置 图形 公共点个数 圆心到直线距离 d与半径r的关系 相交 r •d
O
相切
O
相离 r• d 0
O
r d
•
l
2
1
d<r
交点
d=r
切点
d>r
无 无
公共点名称
直线名称
割线
切线
1、定义： 与圆有且只有一个公 共点的直线是圆的切线.
2、数量关系： 与圆心的距离等于半径 的直线是圆的切线.
B
例1 如图，已知：直线AB经过⊙O上的点C，并 OA=OB，CA=CB。 求证：直线AB是⊙O的切线。
证明：连结OC CA=CB ∵ OA=OB，
O A C B
∴ AB⊥OC于C ∴ 直线AB是⊙O的切线
练一练
1、如图，线段AB经过圆心O，交⊙O于
点A、C，∠BAD＝∠B＝30°，边BD交
圆于点D。BD是⊙O的切线吗？为什么？
F A E
B
O
C
切线的判定方法：
1、定义：和圆有且只有一个公共点的直线是圆的切线。
2、数量关系： 与圆心的距离等于半径的直线是圆的切线。 3、切线的判定定理：
经过半径的外端并且垂直于这条半径的直线是圆的切线。
中考链接
2010北京中考试题
3、如图：在∆ABC中，AB=AC，AE平分 ∠BAC交AB于点E，BM平分∠ABC交AE 于点M，经过B 、M两点的⊙O交BC于点 G，交AB于点F，FB恰好为⊙O的直径. C 求证：AE与⊙O相切.
分析：由于AB过⊙O上的点C，所
以连接OC，只要证明AB⊥OC 即可。
例1 如图，已知：直线AB经过⊙O上的点C，并 OA=OB，CA=CB。 求证：直线AB是⊙O的切线。 证明： 连结OC 在△ AOC和△BOC中 ∵ ∴

切线的概念、切线的判定和性质-人教版九年级数学上册教案一、切线的概念1. 切线的定义在圆上取一点P，连接P与圆心O，若通过点P的直线与圆相交于点P，则这条直线称为该圆在点P处的切线。

2. 切线的性质切线只与圆相交于切点，且垂直于半径。

二、切线的判定1. 判定方法1在圆上任取一点P，连接P与圆心O。

若连接P与圆心O的线段与已知直线L 垂直，则L与圆的交点就是切点，而L即为此点处的切线。

2. 判定方法2在圆上任取一点P，连接P与圆心O。

作过点P并与已知直线L平行的直线，与圆相交于点Q。

再连接点Q与圆心O，则Q与L的交点即为圆在点P处的切点，L即为点P处的切线。

三、切线性质的应用1. 切线定理若一条直线与圆相交于点A、B，则与这条直线垂直的切线分别过点A、B。

2. 判定定理在圆上任取两点P、Q，以这两点为端点连一条线段，若该线段平分圆周角，则它的延长线必过圆的圆心。

3. 弦割定理两条互相垂直的弦互相垂直。

4. 弦长定理两条互相垂直的弦所对圆周的两段弧相等。

5. 弧上点角定理圆周上一点的任意两个角所对的弧长相等。

四、练习题1.已知圆O，半径为3.4cm，P为圆上一点，PA为一条直线，且PA=8.1cm。

求PA的垂线与OP的夹角。

2.已知圆的直径是20cm，D,E,F,G均在圆上。

若DE⊥FG，DE=12cm，FG=9cm，求DG的长。

3.已知圆心角ACB的弧度是20度，线段AB上一点D是圆上的一点，求角ADC的角度。

五、课堂小结1.切线的定义和性质。

2.切线判定方法和定理。

3.切线性质的应用。

4.练习题的解答。

六、作业1.完成课堂练习题。

2.独立思考，将切线定理、判定定理、弦割定理、弦长定理和弧上点角定理的证明写出来。

切线知识点总结一、切线的定义切线是指在几何图形中，与该图形的曲线或曲面相切的直线。

具体来说，在平面上，如果一条直线与一个圆相交，且相交点只有一个，那么这条直线就是圆的切线；在三维空间中，如果一个平面与一个曲面相切，那么这个平面就是曲面的切平面，切平面与曲面交线称为曲面的切线。

二、切线的判定在平面几何中，判断一条直线是否为圆的切线可以采用如下两种方法：1. 使用切线判定定理进行判定。

切线判定定理指出，一条直线与一个圆相切的充分必要条件是这条直线与圆的圆心之间的距离等于圆的半径，即直线与圆的圆心的距离刚好等于圆的半径时，这条直线就是圆的切线。

2. 使用直线方程和圆的方程进行判定。

设圆的方程为(x-a)²+(y-b)²=r², 如果直线的方程为y=kx+m，那么当直线与圆的方程联立时，求得的交点满足系统方程同时成立，那么直线就是圆的切线。

在空间中，判断一个平面是否为曲面的切平面也可以采用相似的方法进行判定。

三、切线的性质1. 切线和圆相切于圆上的点处互相垂直。

如果直线与圆相切于圆上的点处，那么这条直线与圆的切点处的切线互相垂直。

2. 切线与半径的夹角是直角。

在圆的切点处，切线和半径的夹角是90度。

3. 切线的斜率等于曲线在切点处的导数。

在函数的图像中，切线的斜率等于曲线在切点处的导数值。

四、切线的求解1. 在平面几何中，求解一个直线与一个圆的切点位置可以采用切线判定定理，根据直线与圆的方程，通过联立方程求解直线与圆的交点，求得的交点就是切点的位置。

2. 在空间几何中，求解一个平面与一个曲面的切线可以采用类似的方法，根据平面与曲面的方程，求解平面与曲面的交线即可得到曲面的切线。

五、切线的应用1. 在几何学中，切线经常用于证明几何性质，如证明两个圆相切、证明曲线的凹凸性等；2. 在物理学中，切线常用于描述运动过程中的速度、加速度等；3. 在工程学中，切线常用于计算曲线的斜率、弧长等。

切线的判定切线的判定定理 ： 几何符号表达：1、已知：直线AB 经过⊙O 上的点C ，并且OA=OB ，CA=CB 。

求证：直线AB 是⊙O 的切线。

2、已知：O 为∠BAC 平分线上一点，OD ⊥AB 于D,以O 为圆心，OD 为半径作⊙O 。

求证：⊙O 与AC 相切。

总结：(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。

简记为 。

(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。

简记为 。

3、如图，△AOB 中，OA ＝OB ＝10，∠AOB ＝120°，以O 为圆心，5为半径的⊙O 与OA 、OB 相交。

求证：AB 是⊙O 的切线。

4、如图,△ABC 中，AB=AC ，以AB 为直径的⊙O 交边BC 于P ， PE ⊥AC 于E 。

求证:PE 是⊙O 的切线。

A OB C OA BC D O BA COA BCEP5、如图，AB 是⊙O 的直径，OD ⊥弦BC ，∠AEC=∠ODB ，判断直线BD 与⊙O 的位置关系，并给出证明6、已知：如图，在△ABC 中，D 是AB 边上一点，圆O 过D 、B 、C 三点， ∠DOC =2∠ACD =90°。

求证：直线AC 是圆O 的切线；切线的性质切线的性质定理： 几何符号表达：1、以O 为圆心的两个同心圆中，大圆的弦AB 是小圆的切线，点P 是切点， 求证：AP=BP2、如图，AB 为⊙O 的直径，C 为⊙O 上一点，AD 和过C 点的切线互相垂直，垂足为D .求证:AC 平分∠DABO B A CD变式一：如图,AB 为⊙O 的直径, C 为⊙O 上一点,AD ⊥CD ,AC 平分∠DAB . 求证: CD 是⊙O 的切线变式二：如图,AB 为⊙O 的直径, AC 平分∠DAB ,CD 是⊙O 的切线. 求证:AD ⊥CD3、已知:如图, AB 是⊙O 的直径,⊙O 过BE 的中点C ,CD ⊥AE. 求证:DC 是⊙O 的切线.4、已知AB 为⊙O 的直径,DC 切⊙O 于点C,过D 点作 DE ⊥于点F 。