b8中高一(上)自主学习数学试卷(3)

2011-2012学年江苏省徐州一中高一（上）自主学习数学试卷（3）一、填空题（本大题包括14小题；每小题5分，满分70分）1．（5分）已知f（x）=x2+ax+b，满足f（1）=0，f（2）=0，则f（﹣1）=_________．2．（5分）已知函数f（x）=2x+1，则函数f（x2+1）的值域为_________．3．（5分）函数f（x）=x2﹣2ax，x∈[1，+∞）是增函数，则实数a的取值范围是_________．4．（5分）设y=f（x）在x∈[0，1]上的图象如图所示，且f（x）满足f（1﹣x）=f（1+x），则f（x）在[1，2]上的解析式为_________．5．（5分）函数f（x）=x2﹣4x，x∈[0，a]的值域是[﹣4，0]，则a的取值范围为_________．6．（5分）函数y=x2+ax+3（0＜a＜2）在[﹣1，1]的最大值是_________，最小值是_________．7．（5分）已知，则f（x）=_________．8．（5分）已知函数f（x）=若f（2﹣a2）＞f（a），则实数a的取值范围为_________．9．（5分）（2009•黄冈模拟）函数y=ax2﹣2x图象上有且仅有两个点到x轴的距离等于1，则a的取值范围是_________．10．（5分）若函数的定义域为R，则实数m的取值范围是_________．11．（5分）函数y=﹣x2+4ax在区间[2，4]上为单调函数，则实数a的取值范围是_________．12．（5分）函数f（x）=ax2+bx+3a+b（x∈[a﹣1，2a]）的图象关于y轴对称，则f（x）的值域为_________．13．（5分）（2011•安徽模拟）规定符号“△”表示一种运算，即，其中a、b∈R+；若1△k=3，则函数f （x）=k△x的值域_________．14．（5分）（2008•浙江）已知t为常数，函数y=|x2﹣2x﹣t|在区间[0，3]上的最大值为2，则t=_________．二、解答题（本大题包括3小题；每小题10分，满分30分）解答时要有答题过程！15．（10分）用单调性定义证明：函数在区间（0，1）内单调递减．16．（10分）已知函数y=f（x）=x2+ax+3在区间[﹣1，1]上的最小值为﹣3，求实数a的值．17．（10分）（2013•嘉定区一模）已知a∈R，函数f（x）=x|x﹣a|，（Ⅰ）当a=2时，写出函数y=f（x）的单调递增区间；（Ⅱ）当a＞2时，求函数y=f（x）在区间[1，2]上的最小值；（Ⅲ）设a≠0，函数f（x）在（m，n）上既有最大值又有最小值，请分别求出m、n的取值范围（用a表示）．2011-2012学年江苏省徐州一中高一（上）自主学习数学试卷（3）参考答案与试题解析一、填空题（本大题包括14小题；每小题5分，满分70分）1．（5分）已知f（x）=x2+ax+b，满足f（1）=0，f（2）=0，则f（﹣1）=6．考点：二次函数的性质．专题：计算题．分析：由题设可知，由此能求出f（x）=x2﹣3x+2，进而能够求出f（﹣1）．解答：解：∵f（x）=x2+ax+b，满足f（1）=0，f（2）=0，∴，解得a=﹣3，b=2．∴f（x）=x2﹣3x+2，∴f（﹣1）=1+3+2=6．故答案为：6．点评：本昰考查二次函数的性质和应用，解题时要认真审题，合理地建立方程组，先求出f（x），再解f（﹣1）．2．（5分）已知函数f（x）=2x+1，则函数f（x2+1）的值域为[3，+∞）．考点：函数的值域．专题：计算题．分析：根据已知函数先求出函数f（x2+1），再求出函数的值域即可．解答：解：因为函数f（x）=2x+1所以函数f（x2+1）=2（x2+1）+1=2x2+3因为x2≥0所以f（x2+1）=2x2+3≥3所以函数f（x2+1）的值域为[3，+∞）故答案为：[3，+∞）点评：本题以已知函数为载体，考查二次函数的值域，关键是确定函数的解析式，利用二次函数最值的求解方法求函数的值域．3．（5分）函数f（x）=x2﹣2ax，x∈[1，+∞）是增函数，则实数a的取值范围是（﹣∞，1]．考点：二次函数的性质．专题：计算题．分析：f（x）=x2﹣2ax开口向上，对称轴方程x=a，由x∈[1，+∞）是增函数，可得到a所满足的不等式，从而求出实数a的取值范围．解答：解：∵f（x）=x2﹣2ax，∴抛物线开口向上，对称轴方程x=a，∵x∈[1，+∞）是增函数，∴a≤1．故答案为：（﹣∞，1]．点评：本题考查二次函数的性质的应用，解题时要认真审题，仔细解答，注意对称轴和抛物线单调区间的关系的应用．4．（5分）设y=f（x）在x∈[0，1]上的图象如图所示，且f（x）满足f（1﹣x）=f（1+x），则f（x）在[1，2]上的解析式为f（x）=x，x∈[1，2]．考点：函数解析式的求解及常用方法．专题：计算题．分析：从要求的结论f（x）在[1，2]上的解析式不难知道：本题需要知道利用函数的对称性，恰好题中给出了条件f （1﹣x）=f（1+x），因此可知函数的对称性，所以只需求出f（x）在[0，1]上的解析式即可求解．解答：解：由图知，f（x）在[0，1]上的图象是过两点（1，1），（0，2）的线段，斜率为﹣1，在y轴上的截距为2，其解析式为：f（x）=﹣x+2，x∈[0，1]；∵f（x）满足f（1﹣x）=f（1+x），可得f（x）=f（﹣x+2），当1≤x≤2时，0≤﹣x+2≤1，∴f（﹣x+2）=﹣（﹣x+2）+2=x，∴f（x）=x，x∈[1，2]；故答案为：f（x）=x，x∈[1，2]．点评：本题是中档题．考查函数解析式的求解及常用方法、函数的对称性，是道综合题，其中探讨函数的对称性是难点．5．（5分）函数f（x）=x2﹣4x，x∈[0，a]的值域是[﹣4，0]，则a的取值范围为[2，4]．考点：二次函数在闭区间上的最值．专题：计算题．分析：由已知函数的解析式，我们可以判断出函数图象的形状，单调性及最值，根据函数f（x）=x2﹣4x，x∈[0，a]的值域是[﹣4，0]，易结合二次函数的图象和性质得到答案．解答：解：∵函数f（x）=x2﹣4x的图象是开口方向朝上，以直线x=2为对称轴的抛物线；在区间[0，2]上是减函数，在[2，+∞）上是增函数，且f（0）=f（4）=0，f（x）min=f（2）=﹣4，若定义域为[0，a]，值域为[﹣4，0]，则2≤a≤4故答案为：[2，4]．点评：本题考查的知识点是二次函数的性质，其中根据已知条件确定二次函数的图象和性质，是解答本题的关键．6．（5分）函数y=x2+ax+3（0＜a＜2）在[﹣1，1]的最大值是4+a，最小值是．考点：函数的最值及其几何意义．专题：计算题；数形结合．分析：函数y=x2+ax+3（0＜a＜2）的对称轴为x=﹣∈（﹣1，0），其图象开口向上，故最大值为y，最小值为（1）解答：解：函数y=x2+ax+3（0＜a＜2）的对称轴为x=﹣∈（﹣1，0），其图象开口向上，故最大值在x=1时取到，其值为4+a，最小值在x=﹣处取到，其值为，故答案为：4+a，点评：本题考点是函数的最值及其几何意义，考查由图象特征判断并求出函数的最大值与最小值，二次函数在闭区间上的最值问题是高考的热点，做完本题后应认真总结本题的做题规律．7．（5分）已知，则f（x）=x2+2x+2．考点：函数解析式的求解及常用方法．专题：计算题．分析：把式子分组，然后凑完全平方式，最后把原来的换为x即可．解答：解：因为==所以f（x）=x2+2x+2．故答案为：x2+2x+2．点评：本题主要考查凑完全平方式，拼凑法求函数解析式．8．（5分）已知函数f（x）=若f（2﹣a2）＞f（a），则实数a的取值范围为（﹣2，1）．考点：分段函数的解析式求法及其图象的作法；二次函数的性质．专题：计算题．分析：先根据二次函数的解析式分别研究分段函数在各自区间上的单调性，从而得到函数f（x）的单调性，由此性质转化求解不等式，解出参数范围即可．解答：解：函数f（x），当x≥0 时，f（x）=x2+4x，由二次函数的性质知，它在[0，+∞）上是增函数，当x＜0时，f（x）=4x﹣x2，由二次函数的性质知，它在（﹣∞，0）上是增函数，该函数连续，则函数f（x）是定义在R 上的增函数∵f（2﹣a2）＞f（a），∴2﹣a2＞a解得﹣2＜a＜1实数a 的取值范围是（﹣2，1）故答案为：（﹣2，1）点评：本题是奇偶性与单调性结合的一类最主要的题型，利用单调性将不等式f（2﹣a2）＞f（a）转化为一元二次不等式，求出实数a 的取值范围，属于中档题．9．（5分）（2009•黄冈模拟）函数y=ax2﹣2x图象上有且仅有两个点到x轴的距离等于1，则a的取值范围是a＞1或a=0或a＜﹣1．考点：二次函数的图象．专题：数形结合；分类讨论．分析：将a分成a=0，a＞0，与a＜0三种情形分别研究，再结合图象，把握解题的实质，建立关系式，解之即可．解答：解：当a=0时，函数y=﹣2x图象上有且仅有两个点到x轴的距离等于1，满足条件当a＞0时，使函数的最小值即a＞1当a＜0时，使函数的最大值，即a＜﹣1综上所述：a的取值范围是a＞1或a=0或a＜﹣1故答案为：a＞1或a=0或a＜﹣1点评：本题考查了二次函数的图象，通过讨论开口方向，数形结合有助于我们的解题，形象直观．10．（5分）若函数的定义域为R，则实数m的取值范围是．考点：二次函数的性质；一元二次方程的根的分布与系数的关系．专题：计算题．分析：函数的定义域为R等价于mx2﹣6x+2≥0的解集为R，所以，由此能求出实数m的取值范围．解答：解：当m=0时，不符合题意当m≠0时，∵函数的定义域为R，∴mx2﹣6x+2≥0的解集为R，∴，解得m．故答案为：[）．点评：本题考查函数的定义域的逆运算，解题时要认真审题，注意二次函数的性质和一元二次不等式的性质的灵活运用．11．（5分）函数y=﹣x2+4ax在区间[2，4]上为单调函数，则实数a的取值范围是a≤1或a≥2．考点：二次函数的性质．专题：计算题．分析：由已知中函数的解析式y=﹣x2+4ax，根据二次函数的图象和性质，判断出函数y=﹣x2+4ax在区间（﹣∞，2a]为增函数，在区间[2a，+∞）上为减函数，由函数y=﹣x2+4ax在区间[2，4]上为单调函数，可得区间在对称轴的同一侧，进而构造关于a的不等式，解不等式即可得到实数a的取值范围．解答：解：∵函数y=﹣x2+4ax的图象是开口方向朝下，且以x=2a为对称轴的抛物线故函数y=﹣x2+4ax在区间（﹣∞，2a]为增函数，在区间[2a，+∞）上为减函数若函数y=﹣x2+4ax在区间[2，4]上为单调函数，则2a≤2，或2a≥4解得a≤1或a≥2故答案为：a≤1或a≥2点评：本题考查的知识点是二次函数的性质，其中根据函数y=﹣x2+4ax在区间[2，4]上为单调函数，判断出区间在对称轴的同一侧，进而构造关于a的不等式是解答本题的关键．12．（5分）函数f（x）=ax2+bx+3a+b（x∈[a﹣1，2a]）的图象关于y轴对称，则f（x）的值域为．考点：二次函数的性质；二次函数在闭区间上的最值．专题：计算题．分析：由题意可知函数一定为二次函数即a≠0，图象关于y轴对称可判断出b=0，即函数解析式化简成f（x）=ax2+3a，由定义域[a﹣1，2a]关于Y轴对称，得出a的值，求f（x）的值域．解答：解：由题意可知函数一定为二次函数即a≠0，而图象关于y轴对称可判断出b=0，即函数解析式化简成f（x）=ax2+3a．由定义域[a﹣1，2a]关于Y轴对称，故有a﹣1+2a=0，得出a=，即函数解析式化简成f（x）=x2+1，x∈[﹣，]f（x）的值域为[1，]．故答案为：[1，]．点评：此题主要考查函数二次函数图象对称的性质以及二次函数的值域的求法，求解的关键是熟练掌握二次函数的性质，本题理解对称性很关键．13．（5分）（2011•安徽模拟）规定符号“△”表示一种运算，即，其中a、b∈R+；若1△k=3，则函数f （x）=k△x的值域[1，+∞）．考点：函数的值域．专题：计算题；压轴题．分析：先根据1△k=，求得，进而求得k．把k代入f（x）=k△x得出f（x）=+x+1，进而可求得函数f（x）的定义域，再利用配方法求得函数f（x）的值域．解答：解：1△k=，解得=1，∴k=1∴f（x）=k△x==+x+1对于需x≥0，∴对于f（x）=+x+1=（+）2+≥1故函数f（x）的值域为[1，+∞）故答案为：[1，+∞）点评：本题主要考查了函数的值域的问题，以及考查阅读题意的能力，属于创新题．14．（5分）（2008•浙江）已知t为常数，函数y=|x2﹣2x﹣t|在区间[0，3]上的最大值为2，则t=1．考点：分段函数的解析式求法及其图象的作法．专题：压轴题．分析：本题应先画出函数的大体图象，利用数形结合的方法寻找解题的思路．画出大体图象后不难发现函数的最大值只能在x=1或x=3处取得，因此分情况讨论解决此题．解答：解：记g（x）=x2﹣2x﹣t，x∈[0，3]，则y=f（x）=|g（x）|，x∈[0，3]f（x）图象是把函数g（x）图象在x轴下方的部分翻折到x轴上方得到，其对称轴为x=1，则f（x）最大值必定在x=3或x=1处取得（1）当在x=3处取得最大值时f（3）=|32﹣2×3﹣t|=2，解得t=1或5，当t=5时，此时，f（0）=5＞2不符条件，当t=1时，此时，f（0）=1，f（1）=2，符合条件．（2）当最大值在x=1处取得时f（1）=|12﹣2×1﹣t|=2，解得t=1或﹣3，当t=﹣3时，f（0）=3＞2不符条件，当t=1此时，f（0）=1，f（1）=2，符合条件．综上t=1时故答案为：1．点评：本题主要考查二次函数的图象性质和绝对值对函数图象的影响变化．二、解答题（本大题包括3小题；每小题10分，满分30分）解答时要有答题过程！15．（10分）用单调性定义证明：函数在区间（0，1）内单调递减．考点：函数单调性的判断与证明．专题：证明题．分析：任取区间（0，1）内两个实数x1，x2，且x1＜x2，进而根据函数，作差f（x1）﹣f（x2），分解因式后，根据实数的性质，判断f（x1）﹣f（x2）的符号，进而根据函数单调性的定义，即可得到结论．解答：证明：任取区间（0，1）内两个实数x1，x2，且x1＜x2则x1+x2＜2＜，即x1+x2﹣＜0，x1﹣x2＜0 则f（x1）﹣f（x2）=（）﹣（）=（x1+x2﹣）（x1﹣x2）＞0即f（x1）＞f（x2）故函数在区间（0，1）内单调递减点评：本题考查的知识点是函数单调性的判断与证明，其中对作差后的式子，进行因式分解，是利用定义法（作差法）证明函数单调性的难点．16．（10分）已知函数y=f（x）=x2+ax+3在区间[﹣1，1]上的最小值为﹣3，求实数a的值．考点：二次函数在闭区间上的最值．专题：计算题；分类讨论．分析：函数f（x）=x2+ax+3在区间[﹣1，1]上有最小值3，对函数进行配方，对对称轴是否在区间内进行讨论，从而可知函数在何处取得最小值，利用最小值为3建立方程，解出相应的a的值．解答：解：，（1），解得：a=7（2）当，即﹣2≤a≤2时，，解得（舍去）（3）当，即a＜﹣2时，y min=f（1）=4+a=﹣3，解得：a=﹣7．综合（1）（2）（3）可得：a=±7．点评：考查二次函数在闭区间上的最值问题中的动轴定区间上的最值问题，体现了分类讨论和运动变化的思想方法，属中档题．17．（10分）（2013•嘉定区一模）已知a∈R，函数f（x）=x|x﹣a|，（Ⅰ）当a=2时，写出函数y=f（x）的单调递增区间；（Ⅱ）当a＞2时，求函数y=f（x）在区间[1，2]上的最小值；（Ⅲ）设a≠0，函数f（x）在（m，n）上既有最大值又有最小值，请分别求出m、n的取值范围（用a表示）．考点：函数的最值及其几何意义；函数的单调性及单调区间．专题：综合题；数形结合；转化思想；数形结合法；综合法．分析：（I）将a=2代入函数的解析得出f（x）=x|x﹣2|，将其变为分段函数，利用二次函数的图象与性质研究其单调性即可（Ⅱ）当a＞2时，函数y=f（x）在区间[1，2]上解析式是确定的，去掉绝对号后根据二次函数的性质确定其单调性，再求最值．（Ⅲ）a≠0，函数f（x）在（m，n）上既有最大值又有最小值说明在函数最值不在区间端点处取得，在这个区间内必有两个极值，由函数的性质确定出极值，由于极值即为最值，故可借助函数的图象得m、n的取值范围．解答：解：（Ⅰ）当a=2时，f（x）=x|x﹣2|=由二次函数的性质知，单调递增区间为（﹣∞，1]，[2，+∞）（开区间不扣分）（Ⅱ）因为a＞2，x∈[1，2]时，所以f（x）=x（a﹣x）=﹣x2+ax=当1＜≤，即2＜a≤3时，f（x）min=f（2）=2a﹣4当，即a＞3时，f（x）min=f（1）=a﹣1∴（Ⅲ）①当a＞0时，图象如上图左所示由得∴，②当a＜0时，图象如上图右所示由得∴，点评：本题考点是函数的最值及其几何意义，综合考查了二次函数的图象，最值等知识以及配方法求最值的技巧．解题时数形结合，转化灵活，综合性很强．。

4．D
解析：D 【解析】
由 x2 2x 8 >0 得：x∈(−∞,−2)∪(4,+∞)，
令 t= x2 2x 8 ，则 y=lnt，
∵x∈(−∞,−2)时,t= x2 2x 8 为减函数；
x∈(4,+∞)时,t= x2 2x 8 为增函数；
y=lnt 为增函数，
故函数 f(x)=ln( x2 2x 8 )的单调递增区间是(4,+∞)，
本题选择 B 选项.
6．B
解析：B 【解析】 【分析】 由函数的解析式可得函数 f（x）＝x2﹣4x+5＝（x﹣2）2+1 的对称轴为 x＝2，此时，函数取 得最小值为 1，当 x＝0 或 x＝4 时，函数值等于 5，结合题意求得 m 的范围． 【详解】 ∵函数 f（x）＝x2﹣4x+5＝（x﹣2）2+1 的对称轴为 x＝2，此时，函数取得最小值为 1， 当 x＝0 或 x＝4 时，函数值等于 5． 且 f（x）＝x2﹣4x+5 在区间[0，m]上的最大值为 5，最小值为 1， ∴实数 m 的取值范围是[2，4]， 故选：B． 【点睛】 本题主要考查二次函数的性质应用，利用函数图像解题是关键，属于中档题．
a
a
1 a 1. 2
故选：C
【点睛】
本题主要考查对数函数的单调性，涉及到复合函数问题，属于中档题.
2．B
解析：B 【解析】 【分析】 利用换元法求函数解析式，注意换元后自变量范围变化. 【详解】
令 x 2 t ,则 t 2 ，所以 f t t 22 4t 2 5 t2 1,t 2,
则 f x 在[3, 0] 上的解析式为______．
20．己知函数 f x = ax b 的图象经过点(1,3),其反函数 f 1 x 的图象经过点(2.0),则

高一数学自主训练1答案：1-11B A B B B D B A ACBCD ACD12.1（答案不唯一）1314.215.【小问1详解】原式cos cos cos x ===因为π,π2x ⎛⎫∈ ⎪⎝⎭，所以cos 0x <，所以原式cos 1.cos x x ⎛⎫=⋅-=- ⎪⎝⎭【小问2详解】因为1sin cos 5x x +=，所以21(sin cos )25x x +=，即112sin cos 25x x +=，所以12sin cos 25x x =-.所以249(sin cos )12sin cos 25x x x x -=-=.因为π,π2x ⎛⎫∈ ⎪⎝⎭，所以sin 0,cos 0x x ><.所以sin cos 0x x ->.所以7sin cos 5x x -=.所以()()71cos sin cos sin 1cos sin 755tan 12tan sin cos sin cos 1225x x x x x x x x x x x x -⨯-+-=-===-.16.【小问1详解】散点图如下图，最恰当的一个函数模型为②22S av =.将点(30,5)代入22S av =，得2530a =⋅，解得1180a =，所以221180S v =.经检验，表中其余三点的坐标均满足221180S v =，所以最恰当的函数模型为②.【小问2详解】由（1）知，2121115180S S S v v =+=+为v 的增函数.法1：当100v =时，211560100100151809S =⨯+⨯=.因为560519>.所以该车不超速.法2：当51S =时，2115115180v v +=，即212102900v v +-⨯=，所以()()102900v v +-=，又0v ≥.所以90v =.因为90100<.所以该车未超速行驶.17.【小问1详解】依题意，设函数表达式为()32sin 2d A t ωϕ=++，水轮半径为3m ，所以振幅3A =，水轮每分钟按逆时针方向转动1.5圈，故角速度为 1.52ππ6020ω⨯==，水轮上点P 从水中浮现时开始计时，所以π3sin 0020ϕ⎛⎫⨯+= ⎪⎝⎭，且ππ22ϕ-<<，解得π4ϕ=-，所以函数表达式为ππ3sin 2042d t ⎛⎫=-+ ⎪⎝⎭，故ππ323,,,2042A K ωϕ===-=.【小问2详解】根据题意，令πππ2042t -=，可得()15s t =.所以盛水筒出水后至少约15s 就可到达最高点.18.【小问1详解】令0x y ==，代入()()()f x y f x f y +=+可得()00f =，令y x =-，代入()()()f x y f x f y +=+，可得()()()00f x f x f +-==，所以()()f x f x -=-，可得函数()f x 为奇函数；任取12,x x ∈R ，且1221,0x x x x <->，因为()()()f x y f x f y +-=，即()()()()f x y f x f x y x f y ⎡⎤+-=+-=⎣⎦，令21,x x y x x =+=，则21y x x =-，可得()()()2121f x f x f x x -=-，又因为0x >时，()0f x <，且210x x ->，所以()210f x x -<，所以()()210f x f x -<，即()()21f x f x <，所以函数()f x 是R 上的减函数.【小问2详解】()()fx f x -=-，即()()22f x f x -=-，()()()()()()()()22222g x f x m f x f x m f x f x m f x f x =--=-+-=-+-+-()22f x x m =--，令()0g x =，即()()2200f x x m f --==，因为函数()f x 是R 上的减函数，所以220x x m --=，即22m x x =-，令()2222,0,22,0,x x x h x x x x x x ⎧-≥=-=⎨+<⎩则函数()h x 的图象，如图所示，结合图象，可得：当()1,0m ∈-时，函数()g x 有4个零点，即实数m 的取值范围为()1,0-.19.【小问1详解】因为()()1f x f x =--恒成立，得()()111ln 1ln 1x x x a x a x x +--+⎛⎫⎛⎫+=--+ ⎪ ⎪--⎝⎭⎝⎭()()1ln 1ln 1x x x a x a x x +⎛⎫⎛⎫+=--+ ⎪ ⎪+⎝⎭⎝⎭()()11ln 1ln x x x a x a x x ++⎛⎫⎛⎫+=+- ⎪ ⎪⎝⎭⎝⎭所以1a a =-，即12a =.【小问2详解】因为0a =，所以()1ln x f x x x +⎛⎫= ⎪⎝⎭，1ln ln x x t x +⎛⎫= ⎪⎝⎭，得1xx t x +⎛⎫= ⎪⎝⎭1111ln ln ln ln x x x x x sx x x ++++⎛⎫⎛⎫⎛⎫+== ⎪ ⎪ ⎝⎭⎝⎭⎝⎭得11x x s x ++⎛⎫= ⎪⎝⎭因为()111111ln ln ln ln x xx t xx x x x s t s x x x x ++++++⎛⎫⎛⎫⎛⎫===⎪ ⎪⎪⎝⎭⎝⎭⎝⎭；()111111ln ln ln ln x x xsx x x x x t s t x x x x ++++++⎛⎫⎛⎫⎛⎫=== ⎪⎪⎪⎝⎭⎝⎭⎝⎭所以t s s t =.。

【高一】2021 2021学年高一数学上册第一阶段考试题(含答案)【高一】2021-2021学年高一数学上册第一阶段考试题(含答案)天水市市1中学2022年级2022-2022学年第一学期中期考试数学一、（本主题共有10个子主题，每个子主题4分，共40分）1.已知全集，，，则等于（）a、不列颠哥伦比亚省。

2.已知集合，则下列式子表示正确的有（）①②③④a．1个b.2个c.3个d.4个3.给定a={1,2，a2-3a-1}，B={1,3}，a{3,1}，然后a等于（）a．-4或1b．-1或4c．-1d．44.以下四幅图中，功能图为（）a．（1）、（2）、b．（1）、（3）、（4）c．（1）、（2）、（3）d．（3）、（4）5.在以下函数中，区间的递增函数为（）a.b.c.d.6.以下功能组相同（）①与，②与，③与，④与A.①②B①③C②④D①④7.已知a=,b=,c=,则a、b、c的大小关系是（）a、 c>a>bb.c>b>ac.a>b>cd.b>a>c8.如果函数在区间上单调递减，那么实数的取值范围是（）a、不列颠哥伦比亚省。

9.的分数指数幂表示为()a、 b.a3c。

d、都不是10.偶函数在区间[0，4]上单调递减，则有（）a、 b。

c.d.二、问题（本主要问题共有4个子问题，每个子问题4分，共16分）11.函数的定义域为12.如果是主要功能，则13.函数在区间[-3，0]上的值域为14.已知的函数是奇数函数，当时的解析式是三、解答题（共44分）15.（这道题的满分是10分）设,其中xr,如果ab=b，求实数的取值范围．16.（这道题的满分是10分）已知集合，，若，求实数的取值范围。

17.（这道题的满分是12分）已知函数（1）定义领域；(2)判断的奇偶性；18.（这道题的满分是12分）已知函数在闭区间上有最小值3，求实数的值。

一、：acbbdcaaca二、题：11、，12、，13、[-4，0]14、三、解答题15.解：a={0，-4}，ab=B，so ba（i）b=时，4（a+1）2-4(a2-1)<0，得a(ii)b={0}或b={-4}时，0得a=-1；解决方案是（a=.III），{B=.4}综上所述实数a=1或a-1．16.解决方案：（1）当时，有（2）当时有又，则有从上面可以看出17、（1），（2）奇函数18、。

高一数学自主训练4答案1-11B B D B C D C B AC ACDBC12.()23，13.-214.715.⑴当8m =时，(8,3)OC = ，设OC xOA yOB =+ 则1433OC OA OB ∴=-+ ⑵ A 、B 、C 三点能构成三角形,AB AC ∴ 不共线又(1,1),(2,4)AB AC m ==- 141(2)0,6m m ∴⨯-⨯-≠∴≠.16.解：（1）4411()cos cos sin 22f x x x x x m =-+()()22221cos sin cos sin 22x x x x x m =+-+()221cos sin 22x x x m =-++1cos 2222x x m =++πsin 26x m ⎛⎫=++ ⎪⎝⎭.当πsin 216x ⎛⎫+= ⎪⎝⎭时，函数()f x 取到最大值32，所以312m +=，即12m =，令ππ22π,62x k k +=+∈Z ，得ππ,6x k k =+∈Z ，所以当函数()f x 取到最大值时x 的集合为ππ,6x x k k ⎧⎫=+∈⎨⎬⎩⎭Z ∣.（2）由（1）得π1()sin 262f x x ⎛⎫=++ ⎪⎝⎭，所以令222,26πππππ2k x k k -≤+≤+∈Z ，得,3πππ6πk x k k -≤≤+∈Z ，所以函数()f x 的单调递增区间为πππ,π()36k k k ⎡⎤-+∈⎢⎥⎣⎦Z .17.（1）因为02πα<<，3444πππα∴<+<，又1cos 43πα⎛⎫+= ⎪⎝⎭，所以sin 4πα⎛⎫+= ⎪⎝⎭∴1sin sin sin cos cos cos 4444443ππππππαααα⎫⎡⎤⎛⎫⎛⎫⎛⎫=+-=+-+⎪ ⎪ ⎪ ⎪⎢⎪⎝⎭⎝⎭⎝⎭⎣⎦⎝⎭（2）因为cos 243βπ⎛⎫-= ⎪⎝⎭211sin cos cos 22cos 1212242433πβπβπββ⎡⎤⎛⎫⎛⎫⎛⎫=-=-=--=⨯-=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，又因为02πβ-<<，所以cos 3β==，由（1）知，4cos cos cos cos sin sin 4444446ππππππαααα⎡⎤+⎛⎫⎛⎫⎛⎫=+-=+++= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，所以()1cos cos cos sin sin 3αβαβαβ⎛⎫-=+-= ⎪⎝⎭因为02πα<<，02πβ-<<，则0αβπ<-<，所以4αβ-=π．18.解（1）由已知()152,022a b ⎛⎛+=+= ⎝⎭⎝⎭，所以a b+=1414a b +=⎭，即a b + 方向的单位向量为1414⎛ ⎝⎭；（2）由已知1a b ⋅= ，2,1a b == ，所以()()()22222722772157ta b a tb ta t a b tb t t +⋅+=++⋅+=++ ，因为向量27ta b + 与向量a tb + 的夹角为钝角，所以()()270ta b a tb ++< ，且向量27ta b + 不与向量a tb + 反向共线，设()()270ta b k a tb k +=+< ，则27t k kt =⎧⎨=⎩，解得2t =-，从而2215702t t t ⎧++<⎪⎨≠⎪⎩，解得17,,222t ⎛⎛⎫∈--⋃-- ⎪ ⎪⎝⎭⎝⎭.19.解：（1）原方程等价于43155x x⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭43(),()(2)1552x x x x x ϕϕϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭∴=令则是减函数，又.(若直接写出答案扣2分)（2）令()0F x =得33log (31)log (31)x x x a +=+-，∴(31)0x a ->，且2313(31)(33)x x x x x a a +=⋅-=-，整理得23(1)310x x a a ⋅-+-=，令3x t =，则2()(1)1g t at a t =-+-有且仅有一个零点，(0)10g =-<，(1)20g =-<，①当0a >时，0x >，此时，(1,)t ∈+∞且()g t 开口向上，∴()g t 在(1,)+∞上有且仅有一个零点；②当a<0时，0x <，此时，(0,1)t ∈且()g t 开口向下且对称轴方程为11(12x a =+，(0)10g =-< ，(1)20g =-<，故要使()g t 在(0,1)上有且仅有一个零点，只要110112a⎛⎫<+< ⎪⎝⎭且22(1)4610a a a a ∆=++=++=，可得3a =--符合条件；综上：{3(0,)a ∈--⋃+∞.。

高一数学自主训练7答案：1-11B D B D B D D B BCD BC ABC 12.()3,2313.-314.2220232a b +15.【详解】2248343a b ba -+=⋅∴ ，又 ||4a →=，||3b →=，41683943a b ⋅∴⨯-+⨯= ，6a b ∴⋅= 61cos 432b a b a θ⋅∴===⨯ ，又[]0,θπ∈Q ，3πθ∴=；(2)由（1）知：6a b ⋅= ()()a b a b λ-⊥+ ，()()0a b a b λ∴-⋅+= ()2210a a b b λλ⋅∴+--= 即：()166190λλ+--=解得：103λ=.16.【详解】选①，由(2)cos cos b c A a C -=，可得(2sin sin )cos sin cos B C A A C -=，∴()2sin cos sin sin B A A C B =+=，又(0,),sin 0B B π∈≠，∴1cos 2A =，又(0,)A π∈，∴3A π=.选②，由(sin sin )()(sin sin )AB a b cC B +-=-得，()()()a b a b c c b +-=-，∴222b c a bc +-=，∴2221cos 22b c a A bc +-==，又(0,)A π∈，∴3A π=.选③，由题可知ABC π++=，∴()()()tan tan tan 1tan tan tan 1tan tan B C B C B C A B C +=+-=--又tan tan tan 3tan tan A B C B C ++=，∴tan 3A =，又(0,)A π∈，∴3A π=.(2)∵1cos 7B =，即2112sin 27B -=，∴2127sin ,cos 2727B B ==，又点M 在线段AC 上，∠ABM =∠CBM ，573BM =，∴2127sin ,cos 77ABM ABM ∠=∠=，在△ABM 中，327121321sin sin 3272714AMB ABM π⎛⎫∠=+∠=⋅+⋅= ⎪⎝⎭，由正弦定理可得，3213142573c =，∴5c =.17.解：连接ST 、PR ，在RST 中，因为RS PA ⊥，RT PB ⊥，则60SRT ∠= ，由余弦定理可得：22246246cos 6028ST =+-⨯⨯⨯= ，所以，)m ST =.在RST 中，由余弦定理可得，222cos 27ST RT SR STR ST RT +-∠==⋅．在PST 中，()sin sin 90cos PTS STR STR ∠=-∠=∠=由正弦定理可得sin sin120SP ST PTS =∠ ，解得sin sin120ST PTS SP ∠==在直角SPR △中，22222112433PR RS SP ⎛=+=+= ⎝⎭，所以，)m 3PR =.(2)解：因为1sin12024PMN S PM PN PM PN =⋅⋅=⋅ △11462322PMN PRM PRN S S S PM PN PM PN =+=⨯+⨯=+△△△，因为234PM PN PM PN ⋅=+≥，所以，128PM PN ⋅≥，当且仅当PM =)2m 4PMN S PM PN =⋅≥△．18.。

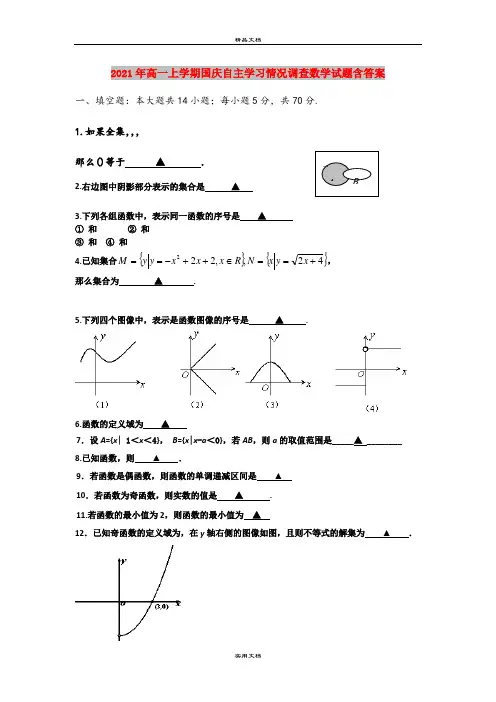
2021年高一上学期国庆自主学习情况调查数学试题含答案一、填空题：本大题共14小题；每小题5分，共70分.1.如果全集，，，那么()等于▲．2.右边图中阴影部分表示的集合是▲3.下列各组函数中，表示同一函数的序号是▲①和②和③和④和4.已知集合{}{}42,,222+==∈++-==xyxNRxxxyyM，那么集合为▲.5.下列四个图像中，表示是函数图像的序号是▲.6.函数的定义域为▲7．设A={x| 1＜x＜4}，B={x|x-a＜0}，若AB，则a的取值范围是_____▲________ 8.已知函数，则▲．9．若函数是偶函数，则函数的单调递减区间是▲10．若函数为奇函数，则实数的值是▲.11.若函数的最小值为2，则函数的最小值为▲12．已知奇函数的定义域为，在y轴右侧的图像如图，且则不等式的解集为▲．UA B13.若的定义域和值域都是[1，]，则▲；14. 函数满足对任意都有成立，则的取值范围是▲ .二、解答题：本大题共6小题；共90分．15、（本题满分14分）已知集合, ,且，求a的值.（答案写在答卷纸上相应的位置）16、（本题满分14分）已知全集为U=，，，求：（1），；（2），.（答案写在答卷纸上相应的位置）17、（本题满分14分）已知函数(1)设集合，求集合；（2）若，求的值域；（3）画出的图象，写出其单调区间。

（答案写在答卷纸上相应的位置）18、（本题满分16分）某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品（百台），其总成本为（万元），其中固定成本为2.8万元，并且每生产1百台的生产成本为1万元（总成本=固定成本+生产成本）．销售收入（万元）满足，假定该产品产销平衡（即生产的产品都能卖掉），根据上述统计规律，请完成下列问题：（1）写出利润函数的解析式（利润=销售收入-总成本）；（2）工厂生产多少台产品时，可使盈利最多？（答案写在答卷纸上相应的位置）19、（本题满分16分）已知函数（Ⅰ）当时，利用函数单调性的定义证明在区间上是单调减函数；（Ⅱ）若函数在区间上是单调增函数，求实数的取值范围。

心尺引州丑巴孔市中潭学校二零二零—二零二壹高一上学期期中自主练习数学试题本卷须知：1.本试题总分值150分，考试时间为120分钟。

2.使用答题纸时，必须使用0.5毫米的黑色签字笔书写，要字迹工整，笔迹清晰。

超出答题区书写的答案无效；在草稿纸、试题卷上答题无效。

3.答卷前将密封线内的工程填写清楚。

一、选择题：本大题共12小题，每题5分，共60分。

在每题给出的四个选项中，只有 一项为哪一项符合题目要求的。

1.集合{}21xA x =>，{}1B x y x ==-，那么()R AC B =A.∅B.(0，1]C.(0，1)D.[1，+∞)2.以下各组函数为相等函数的是A.()f x x =，2()g x x = B.()1f x =，0()(1)g x x =-C.()2()=xf x x，2()()xg x x =D.29()3x f x x -=+，()3g x x =-3.右图是某某年级的三个班在一学期内的六次数学测试的平均成绩y 关于测试序号x 的函数图象，为了容易看出一个班级的成绩变化，将离散的点用虚线连接，根据图象，给出以下结论： ①一班成绩始终高于年级平均水平，整体成绩比较好； ②二班成绩不够稳定，波动程度较大；③三班成绩虽然多数时间低于年级平均水平，但在稳步提升. 其中正确结论的个数为A.OB.1C.2D.34.假设函数2(21)1y x a x =+-+在区间(-∞，2]上是减函数，那么实数a 的取值范围是A.32⎡⎫-+∞⎪⎢⎣⎭， B.3,2⎛⎤-∞-⎥⎝⎦C.3+2⎡⎫∞⎪⎢⎣⎭， D.3,2⎛⎤-∞ ⎥⎝⎦5.假设3log 2a=，lg 0.2b =，0.22c =，那么,,a b c 的大小关系为A.c<b<aB.b<a<cC.a<b<cD.b<c<a6.函数2()2f x ax bx a b =++-是定义在[]1,2a a -上的偶函数，那么a b + =A.13-B.0C.13D.17.幂函数2268()(44)m m f x m m x -+=-+在(0，+∞)为增函数，那么m 的值为A.1或3B.3C.2D.18.函数2220()log 0x x f x x x +⎧≤=⎨>⎩，，，假设0()2f x >，那么0x 的取值范围是A.010x -<≤或04x > B.0014x x <->或 C.004x << D.0-10x <≤9.函数log ()(01)a x xf x a x=<<图象的大致形状是10.函数()lg f x x =，0a b <<，且()()f a f b >，那么A.1ab >B.1ab <C.1ab =D.(1)(1)0a b -->11.设函数1()0x D x x ⎧=⎨⎩，为有理数，为无理数，那么以下结论错误的选项是A.()D x 的定义域为RB.()D x 的值域为{0,1}C.()D x 是偶函数D.()D x 是单调函数A B C D12.设函数()f x 满足对任意的*,N m n ∈，都有()()()f m n f m f n +=⋅，且(1)2f =，那么A.2021B.2017C.4032D.4034二、填空题：本大题共4小题，每题5分，共20分。

高一上期中数学试卷(有答案)高一（上）期中数学试卷一、选择题（共12小题，每小题5分，满分60分）1.已知集合M={1，2，3，4}，N={-2，2}，下列结论成立的是（）A.N⊆MB.M∪N=MC.M∩N=ND.M∩N={2}2.已知集合U=R，P={x|x^2-4x-5≤0}，Q={x|x≥1}，则P∩（∁UQ）（）A.{x|-1≤x＜5}B.{x|1＜x＜5}C.{x|1≤x＜5}D.{x|-1≤x＜1}3.下列函数中表示同一函数的是（）A.y=2x-1B.y=2(x-1)C.y=2x-2D.y=2(x-2)4.已知f(x)=，则f(3)为（）与y=（）4B.y=•D.y=与y=与y=A.3B.4C.1D.25.函数f(x)=2x+x-2的零点所在的一个区间是（）A.（-2，-1）B.（-1，∞）C.（-∞，1）D.（1，2）6.函数g(x)=2015x+m图象不过第二象限，则m的取值范围是（）A.m≤-1B.m<-1C.m≤-2015D.m<-20157.设a=log0.50.9，b=log1.10.9，c=1.10.9，则a，b，c的大小关系为（）A.a＜b＜cB.b＜a＜cC.b＜c＜aD.a＜c＜b8.（）A.（-∞，2]B.（-∞，+∞）C.[2，+∞）D.[0，2]9.一高为H，满缸水量为V的鱼缸截面如图所示，其底部破了一个小洞，缸中水从洞中流出，若鱼缸水深为h时水的体积为v，则函数v=f(h)的大致图象可能是图中四个选项中的（）A。

B。

C。

D。

10.定义在R上的偶函数f(x)满足：对任意的x1，x2∈（-∞，+∞）（x1≠x2），有且f(x1)f(x2)≥0，且对于任意的x∈[0，+∞)，有f(x)f(x+1)≥0，则不等式＜的解集是（）A.（-∞，-2）∪（2，+∞）B.（-∞，-2）∪（1，2）C.（-2，1）∪（2，+∞） D.（-2，1）∪（1，2）11.已知实数a≠0，函数，则f(1-a)=f(1+a)，则a的值为（）A.1B.2C.-1D.-212.设奇函数f(x)在[-1，1]上是增函数，且f(-1)=-1，若对所有的x∈[-1，1]及任意的a∈[-1，1]都满足f(x)≤t^2-2at+1，则t的取值范围是（）A.[-2，2]B.{t|t≤-1或|t|≥1}C.[-∞，∞)D.{t|t≤-2或t≥2或t=0}二、填空题（共4小题，每小题5分，满分20分）13.函数y=|x-a|的图象关于直线x=2对称，则a=2.根据函数$f(x)\geqslant 2$，而且$-x^2-2x+3=-(x+1)^2+4\leqslant 4$，从而求得函数的值域。

阜阳一中2027届高一上学期期中考试数学试题（考试时间：120分钟试卷总分：150分）一、单选题:本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合{}(){}2,128t A xx B t t =≤=≤≤∈Z ∣∣，则A B = （）A ．[]1,3-B ．{}0,1C ．0,2D ．{}0,1,22．命题“[]1,3x ∀∈-，2320x x -+-≤”的否定为（）A ．[]1,3x ∃∈-，0232>-+-x xB ．[]1,3x ∃∈-，2320x x -+-≤C ．[]1,3x ∀∈-，0232>-+-x x D ．[]1,3x ∃∉-，0232>-+-x x 3．“幂函数()()211m f x m m x -=--在()0,∞+单调递减”是“1m =-”的（）A ．充分不必要条件B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件4．下列说法正确的是（）A ．若a b >，则22a b >B ．若22a bc c>，则a b >C ．若a b >，则12a b -<-D ．若a b >，则22ac bc >5．函数e e ex xxy --=的部分图象大致为（）A ．B ．C ．D ．6．若实数a ，b ，c 满足632=⋅=⋅c b a a ，则下列不等关系中不可能成立的是（）A ．c a b<<B ．b c a<<C ．a c b<<D ．a b c<<7．已知函数()f x 的定义域为()()()R,33,63f x f x f -=+=，且(]12,,3x x ∀∈-∞，当12x x ≠时，()()12120f x f x x x ->-，则不等式()263f x x x +->的解集为（）A ．{|1x x <-或>7B ．{}17x x -<<C ．{|0x x <或}6x >D ．{}06x x <<8．从古至今，中国人一直追求着对称美学．世界上现存规模最大、保存最为完整的木质结构——故宫：金黄的宫殿，朱红的城墙，汉白玉的阶，琉璃瓦的顶……沿着一条子午线对称分布，壮美有序，和谐庄严，映衬着蓝天白云，宛如东方仙境．再往远眺，一线贯穿的对称风格，撑起了整座北京城．某建筑物的外形轮廓部分可用函数()f x =+来刻画，满足关于x 的方程()f x b =恰有三个不同的实数根123,,x x x ，且123x x x b <<=（其中,(0,)a b ∈+∞），则b 的值为（）A ．8081-B ．169C ．8081D ．20881二、多选题:本题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9．已知函数1()13xf x =+，则（）A ．31(log 4)5f =B ．()f x 的值域为(,1)-∞C ．()f x 是R 上的减函数D ．函数()f x 图像关于点⎪⎭⎫ ⎝⎛210，对称10．已知0a >，0b >，3a b +=，则（）A ．ab 的最大值为94B C ．3b ba b++的最小值为4D ．2211a b a b +++的最小值为9511．若()f x 定义域为I ，对任意1x I ∈，存在唯一2x I ∈，使得()()121f x f x ⋅=，则称()f x 在定义域上是“倒数函数”，则下列说法正确的是（）A ．1()f x x=是倒数函数B ．1()g x x x=+是倒数函数C ．若21()2x h x x --=+在3,2m ⎡⎤-⎢⎥⎣⎦上是倒数函数，则23m =-D ．若存在0m >，使得2()21(R)s x ax x a =+-∈在定义域[0,]m 上是倒数函数，则1a <-三、填空题：本题共3小题，每小题5分，共15分.12．已知函数()y f x =的定义域为[]0,4，则函数()02y x +=-的定义域是.13．函数21y x ax a =--在12,2⎡⎤--⎢⎥⎣⎦上单调递增，则实数a 的取值范围是.14．设函数()()21,,2,.ax x a f x x x a -+<⎧⎪=⎨-≥⎪⎩若()f x 存在最小值，则a 的取值范围为．四、解答题：本题共5小题，共77分，解答应写出文字说明、证明过程或演算步骤.15．（13分）已知集合{}24A x x =-≤≤，{}322mx B x -=<.（1）当1m =时，求A B ⋂，()A C B U ；（2）当0m >，A B B = 时，求实数m 的取值范围.16．（15分）已知函数()()222,f x ax a x a =-++∈R .(1)对任意[]2,3a ∈，函数()10f x a >-恒成立，求实数x 的取值范围；(2)当a ∈R 时，求不等式()0f x ≥的解集.17．（15分）某文旅公司设计文创作品，批量生产并在旅游景区进行售卖．经市场调研发现，若在旅游季在文创作品的原材料上多投入x 万元()115x ≤≤，文创作品的销售量可增加m 千个，其中14.4,18,120.8,815,xx m x x x ⎧≤<⎪=+⎨⎪-≤≤⎩每千个的销售价格为38m m-万元，另外每生产1千个产品还需要投入其他成本0.5万元．(1)求该文旅公司在旅游季增加的利润y 与x （单位：万元）之间的函数关系；(2)当x 为多少万元时，该公司在旅游季增加的利润最大？最大为多少万元？18．（17分）已知函数21()21x xf x -=+定义域为(1,1)-，函数1()421x xg x m m +=+⋅+-．(1)解不等式(21)(32)0f x f x -+-<；(2)若存在两个不等的实数a ，b 使得()()0f a f b +=，且()()0g a g b +≥，求实数m 的取值范围．19．（17分）已知函数()y f x =与()y g x =的定义域均为D ，若对任意的()1212x x D x x ∈≠､都有()()()()1212g x g x f x f x -<-成立，则称函数()y g x =是函数()y f x =在D 上的“L 函数”.(1)若()43,()2,R f x x g x x D =+==，判断函数()y g x =是否是函数()y f x =在D 上的“L 函数”，并说明理由；(2)若2()21,(),[0,)f x x g x D =-=+∞，函数()y g x =是函数()y f x =在D 上的“L 函数”，求实数m的取值范围；(3)比较a b +和,R a b a b +∈（）的大小，并证明：若()[],0,2f x x D ==，函数()y g x =是函数()y f x =在D 上的“L 函数”，且()()02g g =，则对任意的()1212x x D x x ∈≠､都有()()121g x g x -<阜阳一中2027届高一上学期期中考试数学试题参考答案：1．D【详解】{}{}|2=22A x x xx =≤-≤≤∣，由指数函数的性质可得(){}{}1280,1,2,3t B t t =≤≤∈=Z ∣，所以{}{}{}220,1,2,30,1,2A B xx ⋂=-≤≤⋂=∣.故选：D.2．A【详解】根据全称量词命题的否定形式可知：命题“[]1,3x ∀∈-，2320x x -+-≤”的否定为“[]1,3x ∃∈-，2320x x -+->”，故选：A 3．B【详解】若()f x 为幂函数，则211m m --=，解得1m =-或2m =，因当1m =-时，()2f x x -=在()0,∞+上单调递减，符合题意；当2m =时，()f x x =在()0,∞+上单调递增，不合题意.故由“幂函数()()211m f x m m x -=--在()0,∞+单调递减”当且仅当“1m =-”成立，即“幂函数()()211m f x m m x -=--在()0,∞+单调递减”是“1m =-”的充要条件．故选：B.3．B【分析】ACD 选项可以根据排除法解决，B 选项根据不等式的性质判断.【详解】A 选项，取0,1a b ==-，满足a b >，但是22a b <，A 选项错误；B 选项，显然0c ≠，则20c >，根据不等式的性质，不等式22a bc c>两边同时乘以2c 可得，a b >，B 选项正确；C 选项，取0,1a b ==-，11a -=-，23b -=-，此时12a b ->-，C 选项错误；D 选项，若0c =，则22ac bc =，D 选项错误.故选：B 5．A【详解】e e ()ex xxf x --=定义域为R ，且e e ()()ex xxf x f x ---==-，则原函数为奇函数.排除B.再取特殊值1112e e 1(1)11e e f --==-<，且为正数.排除D.当0x >时，2e e 1()11e ex x xx f x --==-<，x 越大函数值越接近1，排除C.故选：A.6．D【详解】由已知得623b ca==，易知0a >，设直线l ：6y a=，作出2x y =，3x y =，直线l 图象，如图：当61a>时，06a <<，0c b <<，当601a<<时，6a >，0b c <<，所以a b c <<不可能成立，故选:D.7．D【分析】根据函数的对称性、单调性、图象等知识求得不等式的解集.【详解】依题意，函数()f x 的定义域为()()R,33f x f x -=+，所以()f x 的图象关于直线3x =对称，(]12,,3x x ∞∀∈-，当12x x ≠时，()()12120f x f x x x ->-，所以()f x 在区间(],3-∞上单调递增，则()f x 在区间()3,∞+上单调递减，对于不等式()263f x x x +->，即()()236f x x >--，设()()236g x x =--，()g x 的开口向上，对称轴为直线3x =，()()063g g ==，()()()()6333303f f f f =+=-==，由此画出()f x 的大致图象、()g x 的图象如下图所示，由图可知()()f x g x >的解集为{}|06x x <<.故选：D8．B【详解】因为()()2f x a f x +=+==-，所以()f x 关于x a =对称，所以()f x b =的根应成对出现，又因为x 的方程()f x b =恰有三个不同的实数根123,,x x x 且123x x x b <<=，所以该方程的一个根是a ，得1232,,x x b a a x b ==-=，且a b ≠，所以()()f a b f b b⎧===⎪⎨=+=⎪⎩，由()f a b ==得24b a =，当20b a -≥，即2042b b -⨯≥，即02b <≤时，()f b b =+=，①2242b b b -⨯===-，②由①-②得32b =，解得169b =，所以6481a =；当20b a -<，即2042b b -⨯<，即2b >时，()f b b =+=，③222422b bb b ⨯-===-，④由③-④得22b=+，即)220=，解得4b =，此时244b a b ===，不合题意，舍去，综上，6416,819a b ==.故选：B.9．ACD【详解】33log 4111(log 4)14513f ===++，所以选项A 正确；13x y =+的值域是(1,)+∞，故1()13xf x =+的值域是(0,1)，所以选项B 错误；13x y =+恒正且在R 上递增，故113xy =+是R 上的减函数，所以选项C 正确；由于1113()()113131313xx x x xf x f x -+-=+=+=++++，所以选项D 正确．故选：ACD 10．ACD 【详解】A 选项，0a >，0b >，()2944a b ab +≤=，当且仅当32a b ==时，等号成立，A 正确；B 选项，233a b =+++，>B 错误.C 选项，3224b b b a b b b a a b a b a b ++++=+=++≥=，当且仅当b aa b =，即32a b ==时，等号成立，C 正确；D 选项，()()()()2222121111121111a b a b b a b a a b +++=+++-++-++++114111111111a b a b a b =+++++-=++++++，其中0a >，0b >，3a b +=，故11155a b +++=，所以()()11511111121155111515a b a b b b a b a a ++++⎛⎫+⎛⎫+=+ ⎪+=++ ⎭⎪⎝+++⎝++⎭2455≥+=，故22119111115a b a b a b +=++≥++++，当且仅当()()115151a b b a ++=++，即32a b ==时，等号成立，D 正确.故选：ACD 11．ACD【详解】由题意对任意1x I ∈，存在唯一2x I ∈，使得()()121f x f x ⋅=，则称()f x 在定义域上是“倒数函数”，则()f x 在定义域上是“倒数函数”当且仅当对任意1x I ∈，存在唯一2x I ∈，使得()()121f x f x =；即当且仅当()f x 的值域是()()11f x f x =的值域的子集，定义()f x 的值域、()()11f x f x =的值域分别为1,f f R R ，所以()f x 在定义域上是“倒数函数”当且仅当1f f R R ⊆；对于A ，1()f x x=的值域为()(),00,f R ∞∞=-⋃+，而()()11,0f x x x f x ==≠的值域为()()1,00,f R ∞∞=-⋃+，显然满足1f f R R ⊆，故A 正确；对于B ，由对勾函数性质可得，1()g x x x=+的值域为(][),22,g R ∞∞=--⋃+，而()()11g x g x =的值域为111,00,22g R ⎡⎫⎛⎤=-⋃⎪ ⎢⎥⎣⎭⎝⎦，不满足1g g R R ⊆，故B 错误；对于C ，由题意21()2x h x x --=+在3,2m ⎡⎤-⎢⎥⎣⎦上是倒数函数，首先当3,2x m ⎡⎤∈-⎢⎥⎣⎦时，()223213()2222x x h x x x x -++--===-++++单调递减，此时21,42h m R m --⎡⎤=⎢⎥+⎣⎦，由倒数函数定义可知，21,42h m R m --⎡⎤=⎢⎥+⎣⎦不包含0，即2102m m -->+（1）；从而()()11h x h x =在3,2x m ⎡⎤∈-⎢⎥⎣⎦时的值域为112,421h m R m +⎡⎤=⎢⎥--⎣⎦，由题意12112,4,2421h h m m R R m m --+⎡⎤⎡⎤=⊆=⎢⎥⎢⎥+--⎣⎦⎣⎦，所以要满足题意，还需满足211242421m m m m --⎧≥⎪⎪+⎨+⎪≥⎪--⎩（2）；只需（1）（2）式子同时成立即可，所以当且仅当2421m m +=--，解得23m =-，故C 正确；对于D ，必要性：情形一：当0a >时，2()21(R)s x ax x a =+-∈在定义域()[0,],0m m >上单调递增，则()1,s R s m ⎡⎤=-⎣⎦，若2()21(R)s x ax x a =+-∈在定义域[0,]m 上是倒数函数，首先()0s m <，此时()()11s x s x =的值域为()11,1s R s m ⎡⎤=-⎢⎥⎢⎥⎣⎦，同时注意到()()111,,1s s R s m R s m ⎡⎤⎡⎤=-⊆=-⎢⎥⎣⎦⎢⎥⎣⎦不成立，故0a >不符合题意；情形二：当0a =时，()21s x x =-在定义域()[0,],0m m >上单调递增，则()1,s R s m ⎡⎤=-⎣⎦，若2()21(R)s x ax x a =+-∈在定义域[0,]m 上是倒数函数，首先()0s m <，此时()()11s x s x =的值域为()11,1s R s m ⎡⎤=-⎢⎥⎢⎥⎣⎦，同时注意到()()111,,1s s R s m R s m ⎡⎤⎡⎤=-⊆=-⎢⎥⎣⎦⎢⎥⎣⎦不成立，故0a =不符合题意；情形三：当0a <时，注意到2()21(R)s x ax x a =+-∈的对称轴为10x a=->，则()20f f a ⎛⎫=- ⎪⎝⎭，（i ）当20m a<≤-时，()()min 01s x s ==-，由二次函数性质可知存在0[0,]x m ∈使得()()0max s x s x =，即此时()01,s R s x ⎡⎤=-⎣⎦，若2()21(R)s x ax x a =+-∈在定义域[0,]m 上是倒数函数，首先()00s x <，此时()()11s x s x =的值域为()101,1s R s x ⎡⎤=-⎢⎥⎢⎥⎣⎦，同时注意到()()10011,,1s s R s x R s x ⎡⎤⎡⎤=-⊆=-⎢⎥⎣⎦⎢⎥⎣⎦不成立，故20m a <≤-不符合题意；（ii ）当20m a>->时，由二次函数性质可知()()()2minmax1121,1s x s m am m s x s a a ⎛⎫==+-=-=-- ⎪⎝⎭，即此时()1,s R s m s a ⎡⎤⎛⎫=- ⎪⎢⎥⎝⎭⎣⎦，注意到()01s s R =-∈，若2()21(R)s x ax x a =+-∈在定义域[0,]m 上是倒数函数，首先1110s a a ⎛⎫-=--< ⎪⎝⎭，其次结合0a <，可得a 应该满足1a <-；充分性：1a ∀<-，有11110s a a ⎛⎫-<-=--< ⎪⎝⎭，20m a∃>->，使得()22211222111021am am m am m s m am m <-⇒<-⇒+-<-⇒-<=<+-，这表明当1a <-时，存在0m >，使得2()21(R)s x ax x a =+-∈在定义域[0,]m 上是倒数函数，故D 正确.故选：ACD.12．11,2⎡⎫-⎪⎢⎣⎭【详解】21y x ax a =-- 在12,2⎡⎤--⎢⎥⎣⎦上单调递增，∴2()f x x ax a =--在12,2⎡⎤--⎢⎥⎣⎦单调递减，则122a-≤，即1a ≥-，同时需满足1(2)()02f f -->，即1(4)(21)04a a +-<，解得142a -<<，综上可知11,2a ⎡⎫∈-⎪⎢⎣⎭故答案为：11,2⎡⎫-⎪⎢⎣⎭14．01a ≤≤【详解】解：若0a =时，21,0(){(2),0x f x x x <=-≥，∴min ()0f x =；若0a <时，当x a <时，()1f x ax =-+单调递增，当x →-∞时，()f x →-∞，故()f x 没有最小值，不符合题目要求；若0a >时，当x a <时，()1f x ax =-+单调递减，2()()1f x f a a >=-+，当x a >时，min 20(02)(){(2)(2)a f x a a <<=-≥∴210a -+≥或2212a a -+≥-（），解得01a <≤，综上可得01a ≤≤；15．（1）{}24A B x x ⋂=-≤<，(){}4≠=x x A C B U ；（2）()0,1.【详解】（1）当1m =时，322mx -<，即322x -<解得31x -<，即4x <，则{}4B x x =< (3){}24A B x x ∴⋂=-≤<，又{}42><=x x x A C U 或(){}4≠=∴x x A C B U ； (8)（2）由322mx -<解得4mx <，又0m > ，4x m∴<，即4{|}B x x m =<，由A B B = 得A B ⊆， (11)44m∴>，1m <，01m ∴<<，即m 的取值范围是()0,1. (13)16．(1)()(),13,∞∞--⋃+(2)答案见解析【详解】（1）依题意，()22210ax a x a -++>-恒成立，()21280xx a x -+⨯-->恒成立，又因为2213124x x x ⎛⎫-+=-+ ⎪⎝⎭恒大于0，所以()212280x x x -+⨯-->，即()(),13,x ∞∞∈--⋃+. (6)（2）()()()()22212f x ax a x x ax =-++=--，当0a =时，()22f x x =-+，由()0f x ≥，解得1x ≤：当0a ≠时，令()0f x =，解得1221,x x a==.当0a <时，201a<<，即21x x <由()0f x ≥，解得21x a ≤≤；当02a <<时，21>a，即21x x >，解得2x a ≥或1x ≤当2a =时，21a=，由()0f x ≥，解得∈；当2a >时，21a<，即21x x <，由()0f x ≥，解得2x a ≤或1x ≥综上所述：当0a <时，不等式()0f x ≥的解集为2,1a ⎡⎤⎢⎥⎣⎦；当0a =时，不等式()0f x ≥的解集为(],1-∞；当02a <<时，不等式()0f x ≥的解集为(]2,1,a ∞∞⎡⎫-⋃+⎪⎢⎣⎭；当2a =时，不等式()0f x ≥的解集为；当2a >时，不等式()0f x ≥的解集为[)2,1,a ∞∞⎛⎤-⋃+ ⎥⎝⎦ (15)17．(1)368,18144 3.5,815xx x y x x x ⎧--≤<⎪=+⎨⎪-≤≤⎩(2)当5x =（万元）时，该公司在旅游季增加的利润最大，最大为17万元.【详解】（1）本季度增加的利润830.5 2.58y m m x m x m ⎛⎫=---=-- ⎪⎝⎭，当18x ≤<时，14.4362.58811x xy x x x x =⨯--=--++，当815x ≤≤时，()2.520.8844 3.5y x x x =---=-，所以该公司增加的利润y 与x （单位：万元）之间的函数关系式为368,18144 3.5,815xx x y x x x ⎧--≤<⎪=+⎨⎪-≤≤⎩； (7)（2）368,18144 3.5,815xx x y x x x ⎧--≤<⎪=+⎨⎪-≤≤⎩，当18x ≤<时，()363682912921711x y x x x x ⎡⎤=--=-++≤-⎢⎥++⎣⎦，当3611x x =++，即5x =时，等号成立， (11)当815x ≤≤时，44 3.5y x =-是减函数，当8x =时，取得最大值16， (13)因为1716>，所以当5x =（万元）时，该公司在旅游季增加的利润最大，最大为17万元 (15)18．(1)1335x x ⎧⎫<<⎨⎬⎭⎩(2)25+12∞⎛⎫- ⎪⎝⎭，【详解】（1）函数21()21x x f x -=+定义域为(1,1)-，关于原点对称，212122()1212121x x x x xf x +--===-+++，所以易知，()f x 在(1,1)-上单调递增，因为()2112()2112x xx xf x f x -----===-++，()f x 是奇函数，由(21)(32)0f x f x -+-<可得()(21)(32)23f x f x f x -<--=-，所以121112312123x x x x-<-<⎧⎪-<-<⎨⎪-<-⎩，解得：1335x <<.故不等式的解集为：1335x x ⎧⎫<<⎨⎬⎭⎩. (7)（2）由()()0f a f b +=可得()()()f a f b f b =-=-，所以=-b a ，不妨设a b >，则01a <<，因为1()421x x g x m m +=+⋅+-，令122aat =+，则522t <<，所以，11()()()()421421a a a a g a g b g a g a m m m m +--++=+-=+⋅+-++⋅+-211=222222a a a am m ⎛⎫⎛⎫+++- ⎪ ⎪⎝⎭⎝⎭()2210t m t =+-≥， (12)所以222t m t≥-，令()22211=2222111222t h t t t t t ==-⎛⎫--- ⎪⎝⎭，因为522t <<，所以21152t <<，所以2111112222225t ⎛⎫-<--<- ⎪⎝⎭，所以()25212h t -<<-，所以2512m >-所以实数m 的取值范围为：25+12∞⎛⎫- ⎪⎝⎭ (17)19．(1)是，理由见解析(2)116m ≥(3)||||||a b a b +≥+，证明见解析【详解】（1）对任意的12R x x ∈､，且12x x ≠，()()12122g x g x x x -=-，()()12124f x f x x x -=-.显然有()()()()1212g x g x f x f x -<-，所以函数()y g x =是函数()y f x =在D 上的“L 函数”. (3)（2）因为函数()y g x =是函数()y f x =在D 上的“L 函数”，所以()()()()1212g x g x f x f x -<-对任意的[)()12120,x x x x ∞∈+≠､恒成立，22122x x <-对任意的[)()12120,x x x x ∞∈+≠､恒成立，22122x x <-对任意的[)()12120,x x x x ∞∈+≠､恒成立，12>对任意的[)()12120,x x x x ∞∈+≠､恒成立，即12≥，解得116m ≥ (8)（3）因为0a b +≥，0a b +≥，所以()2222a b a b ab ab +-+=-.所以当0ab ≥时，()22220a b a b ab ab +-+=-=.当0ab <时，()222240a b a b ab ab ab +-+=-=->.综上：a b +≥a b +. (11)对于[]120,2x x ∈､，不妨设12x x >，（i ）当1201x x <-≤时，因为函数()y g x =是函数()y f x =在[]0,2上的“L 函数”，所以()()1212|1g x g x x x -<-≤∣.此时()()121g x g x -<成立； (13)（ii ）当121x x ->时，由[]120,2x x ∈､得1212x x <-≤，因为()()02g g =，函数()y g x =是函数()y f x =在[]0,2上的“L 函数，所以()()()()()()121220g x g x g x g g g x -=-+-()()()()1220g x g g g x ≤-+-()()12121220221x x x x x x <-+-=-+=--<，此时()()121g x g x -<也成立，综上，()()121g x g x -<恒成立. (17)。

2021年高一上学期第三次考试数学试题含答案一、选择题（共12小题，每小题5分，共60分）1．已知第一象限角，锐角，小于90°的角，那么关系是（）A．B．C．≠D．2．的值（）A. 小于B. 大于C. 等于D. 不存在3．化简的结果是( )A．B．C．D．4．函数的周期、振幅、初相分别是（）A. B.C. D.5．函数的图象（）A．关于原点对称B．关于点（，0）对称C．关于轴对称D．关于直线对称6．为的一个内角,若,则这个三角形的形状为（）A. 锐角三角形B. 钝角三角形C. 等腰直角三角形D. 等腰三角形7．要得到函数的图象，只需将的图象( )A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度8．（A＞0，ω＞0）在x=1处取最大值，则（）A．一定是奇函数B．一定是偶函数C．一定是奇函数D．一定是偶函数9．已知函数的图象如图所示，则函数的图象可能是（）A. B. C. D.10．当时，不等式的解集是（）A．B．C．D．11．已知函数，又为锐角三角形两锐角则（）A．B．C．D．12．在直角坐标系中, 如果两点在函数的图象上, 那么称为函数的一组关于原点的中心对称点(与看作一组). 函数关于原点的中心对称点的组数为( )A．1 B．2 C．3 D．4二、填空题（共4小题，每小题5分，共20分）13．如图，点O为作简谐振动的物体的平衡位置，取向右O方向为正方向，若振幅为3cm ，周期为4s ，且物体向右运动到距平衡位置最远处时开始计时．则该物体10s 时刻的路程为 cm ．14. 已知函数)||,0,0)(sin()(πϕωϕω<>>+=A x A x f 在一个周期内的图象如图所示,则该函数的解析式为____________________.15.已知函数在区间内至少取得两次最小值，且至多取得三次最大值，则的取值范围是______________16．已知函数，下列命题中正确的是 （写出所有正确命题的序号）①在（）上有3个零点；②的图象关于点对称；③的周期为；④在（）上单调递增．三、解答题（共6小题，共70分）17.（10分）已知，求值：（1）； （2）.18.（12分）已知，且满足，（1）求的值；（2）求的值.19. （12分） 有两个函数()sin(),()tan()(0)34f x a kx g x b kx k ππ=+=->，它们的最小正周期之和为，且满足，求这两个函数的解析式，并求的对称中心坐标及单调区间.20. （12分） 已知点,是函数 图象上的任意两点,且角的终边经过点,若时,的最小值为.（1）求函数的解析式；（2）求函数的单调递增区间；（3）求当时，的值域.21. （12分）已知函数，其中且.（1）当时，求函数的值域；（2）当在区间上为增函数时，求实数的取值范围.22. （12分）已知函数，其中.（1）若，且的最大值为，最小值为，试求函数的最小值；（2）若对任意实数，不等式恒成立，且存在使得成立，求的值；（3）对于问（1）中的，若对任意的，恒有，求的取值范围．南昌二中xx 学年度上学期第三次考试高一数学试卷参考答案1—5 BABDD 6—10 BBDCD 11—12 BB13. 30 14. 15. 16. ②③④17.解：由知，，（1）化简原式；（2）原式18.解：（1）令，则 ∴即等价于，也即解得：或，又∵，舍去，故成立，即（2）233111sin cos (sin cos )(1sin cos )(1)216t t αααααα-+=+-=-=-. 19.解：依题意可得：23,sin(2)tan()32435sin()tan()223124k k k a k b k a k b πππππππππππ⎧+=⎪⎪⎪+=-⎨⎪⎪+=--⎪⎩解得：故()2sin(),())34f x x g x x ππ=+=- 令，得，故的对称中心坐标为，当时，单调递增，即当时，单调递增，无递减区间.20.解：（1）角的终边经过点，， ，.由时,的最小值为，得，即，∴(2）,即,函数的单调递增区间为(3 ) 当时, ，由图像（或由函数单调性），易得，所以函数的值域为.21.解：（1）当时，真数2221111[(1)1]022ax x x x x -+=-+=-+>恒成立，故定义域为，又∵真数，且函数在单调递减∴，即函数的值域为；（2）依题意可知，i ）当时，由复合函数的单调性可知，必须在上递增，且对恒成立故有解得：ii)当时，由同理必须在上递减，且对恒成立故有解得：综上，实数的取值范围为.22.解：(1)由，得，又故当时，；……①当时，；……②由①式+②式，得，又且，∴，带入①式，得∴，则；（2）由题意可知，当且仅当，即时，，也即，得，……③又对恒成立，故 ……④由③式知，代入④式，得，∴ ……⑤又∵,使得成立，也即有解由，讨论如下：i)若，由③，⑤式知，，则22200000(2)221(1)0a x bx c x x x -++-=-+-=--<显然有解，符合题意；ii ）若，由③，⑤式知，，则，显然不存在，舍去；iii) 若,由⑤式知，，又由③式，得，这与条件中矛盾，舍去. 故，也即.（3）由(1)知，，则题意即为，化简为：对恒成立令，则只需成立，也即解得：故的取值范围为.%}23366 5B46 孆 40333 9D8D 鶍X22111 565F 噟24705 6081 悁31403 7AAB 窫34528 86E0 蛠26407 6727 朧ys32211 7DD3 緓。

高一（上）数学期中考试卷（含答案）第I 卷（选择题）一、单选题（本大题共12小题，共48.0分。

在每小题列出的选项中，选出符合题目的一项）1. 已知集合A ={x|x+2x−4≤0}，B ={0,1,2,4,8}，则A ∩B =( ) A. {1,2,4,8} B. {0,1,2} C. {1,2} D. {0,1,2,4}2. 命题“∃x 0∈R,1<2x 0≤2”的否定形式是( )A. ∀x ∈R ，1≥2x >2B. ∃x 0∈R,1<2x 0≤2C. ∃x 0∈R,2x 0≤1或2x 0>2D. ∀x ∈R ，2x ≤1或2x >23. 已知a ，b ∈R ，则“log 2a >log 2b ”是“(13)a <(13)b ”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. 若正数a ，b 满足a +b =1，则9a +1b的最小值为( )A. 16B. 13C. 20D. 155. 若不等式ax 2+bx +c >0的解集为{x|2<x <5}，则不等式cx 2+bx +a >0的( )A. {x|−12<x <−15} B. {x|x <−12或x >−15} C. {x|15<x <12}D. {x|x <15或x >12}6. 在下列四个函数中，与f(x)=x 表示的是同一函数的个数是( )①g(x)=√x 2 ②ℎ(x)=(√x)2 ③m(x)=√x 33④p(x)=x 2xA. 0B. 1C. 2D. 37. 已知f(x)={(5a −1)x +2a,x ≤1log a x,x >1(a >0,a ≠1)是减函数，则a 的取值范围是( ) A. (0,17]B. (0,15)C. [17,1)D. [17,15)8. 已知f(x +2)是偶函数，当2<x 1<x 2时，f(x 2)−f(x 1)x2−x 1>0恒成立，设a =f(12)，b =f(3)，c =f(4)，则a 、b 、c 的大小关系为( )……○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※……○…………内…………○…………装…………○…………订…………○…………线…………○…………A. b <a <cB. c <b <aC. b <c <aD. a <b <c9. 已知幂函数y =(m 2−2m −2)x m2+m−1在(0,+∞)单调递增，则实数m 的值为( )A. −1B. 3C. −1或3D. 1或−310. 已知a =20.1，b =log 0.30.5，c =log 0.50.2，则( )A. c >b >aB. b >c >aC. c >a >bD. a >c >b11. 已知函数f(x 2+1)的定义域为[1,2]，则函数g(x)=f(x)lg(x−2)的定义域为( )A. [2,5]B. (2,3)∪(3,5]C. (2,5]D. [2,3)∪(3,5]12. 已知函数f(x)=x 2−(a +b)x +ab 满足f(1)<0(其中0<a <b)，则函数g(x)=a x +b −1的图象可能为( )A.B.C.D.第II 卷（非选择题）二、填空题（本大题共3小题，共12.0分）13. 计算：log 2.56.25+lg0.001+ln √e +2−1+log 23=______．14. 已知f(x)是奇函数，且当x <0时，f(x)=−e ax .若f(ln2)=8，则a = ．15. 函数f(x)=log 13(6−x −x 2)的单调递增区间是______ ．三、解答题（本大题共4小题，共40.0分。

师大附中高一自主招生考试数学测试题本卷满分150分 考试时间100分钟题号 一 二 三总 分 复 核 1 2 3 4 5 得分 阅卷教师一、选择题（每小题6分，共30分。

每小题均给出了代号为A 、B 、C 、D 的四个选项，其中有且只有一个选项是正确的。

请将正确选项的代号填入题后的括号里，不填、多填或错填均得0分）一、选择题（每小题5分，满分40分。

以下每小题均给出了代号为A ，B ，C ，D 的四个1、已知四边形1S 的两条对角线相等，但不垂直，顺次连结1S 各边中点得四边形2S ，顺次连结2S 各边中点得四边形3S ，以此类推，则2006S 为（ ）A ．是矩形但不是菱形； B. 是菱形但不是矩形； C.既是菱形又是矩形； D.既非矩形又非菱形. 2、方程1)1(32=-++x x x 的所有整数解的个数是（ ） A.．5个 Ｂ．4个 Ｃ．3个 Ｄ．2个3、若1xy ≠，且有272009130x x ++=及213200970y y ++=，则xy的值是 （ ） A ．137 B ．713 C ．20097- D ．200913- 4.如图，△AOB 和△ACD 均为正三角形，且顶点B 、D 均在双曲线)0(4>=x xy 上，则图中S △OBP = ．A .32B .33C .34D .4二、填空题（每小题6分，共36分）（3）=33134=+，f （13）=1131413=+， 1、对于正数x ，规定f （x ）=x1x+,例如f 计算f （12006）+ f （12005）+ f （12004）+ …f （13）+ f （12）+ f （1）+ f （1）+ f （2）+ f （3）+ … + f （2004）+ f （2005）+ f （2006）= .2、函数y ＝224548x x x x +++-+的最小值是____________3．=+++34716251 ．三、解答题（共6题，10+10+13+13+15+15=74分）15、已知关于x 的方程022=-++a a x x 和0)2)(12()13(2=-++--a a x a x 。

2020-2021学年高一数学上学期第一次阶段测试试题一、选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．若集合A 、B 、C 满足A ∩B ＝A ，B ∪C ＝C ，则A 与C 之间的关系是( )A ．A ＝CB ．C ≠AC ．A ⊆CD ．C ⊆A2．已知集合A ，B 均为全集U ＝{1,2,3,4}的子集，且∁U (A ∪B )＝{4}，B ＝{1,2}，则A ∩∁U B ＝( )A ．{3}B ．{4}C ．{3,4}D ．∅3．函数f (x )＝|x －1|的图象是( )4．若函数f (x )满足f (3x ＋2)＝9x ＋8，则f (x )的解析式是( )A ．f (x )＝9x ＋8B ．f (x )＝3x ＋2C ．f (x )＝－3x －4D ．f (x )＝3x ＋2或f (x )＝－3x －45．函数f (x )＝1＋x ＋1x的定义域是( ) A ．[－1，＋∞) B ．(－∞，0)∪(0，＋∞)C ．[－1,0)∪(0，＋∞)D ．R6．已知函数f (x )＝1x在区间[1,2]上的最大值为A ，最小值为B ，则A －B 等于( ) A.12 B ．－12C ．1D ．－1 7．已知偶函数y ＝f (x )在[0,4]上是增函数，则一定有( )A ．f (－3)＞f (π) B．f (－3)＜f (π)C ．f (3)＞f (－π) D．f (－3)＞f (－π)8．函数y ＝f (x )是R 上的偶函数，且在(－∞，0]上是增函数，若f (a )≤f (2)，则实数a 的取值范围是( )A ．a ≤2B ．a ≥－2C ．－2≤a ≤2D ．a ≤－2或a ≥2二、填空题(本大题共2小题，每小题5分，共10分)9．设集合A ＝{x |1＜x ＜2}，B ＝{x |x ＜a }，满足A ⊆B ，则实数a 的取值范围是______．10．设函数f (x )＝⎩⎪⎨⎪⎧ x 2＋2，x ≥2，2x ，x <2，已知f (x 0)＝8，则x 0＝________.三、解答题(本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤)11．(本小题10分)已知全集U ＝{x |x －2≥0或x －1≤0}，A ＝{x |x <1或x >3}，B ＝{x |x ≤1或x >2}，求A ∩B ， (∁U A )∩(∁U B )，12、(本小题12分已知全集U ＝R ，集合A ＝{x |－2≤x ≤5}，B ＝{x |a ＋1≤x ≤2a －1}且A ⊆∁U B ，求实数a 的取值范围．13．(本小题12分)已知函数f (x )＝x ＋m x ，且f (1)＝3.(1)求m ；(2)判断函数f (x )的奇偶性．14．(本小题12分)函数f (x )是R 上的偶函数，且当x >0时，函数的解析式为f (x )＝2x －1. (1)用定义证明f (x )在(0，＋∞)上是减函数；(2)求当x <0时，函数的解析式．15．(本小题12分) 某市乘出租车计费规定：2公里以内5元，超过2公里不超过8公里的部分按每公里1.6元计费，超过8公里以后按每公里2.4元计费．若甲、乙两地相距10公里，则乘出租车从甲地到乙地共需要支付乘车费为多少元？16．(本小题12分) 设函数f (x )的定义域为R ，并且图象关于y 轴对称，当x ≤－1时，y ＝f (x )的图象是经过点(－2,0)与(－1,1)的射线，又在y ＝f (x )的图象中有一部分是顶点在(0,2)，且经过点(1,1)的一段抛物线．(1)试求出函数f (x )的表达式，作出其图象；(2)根据图象说出函数的单调区间，以及在每一个单调区间上函数是增函数还是减函数．高一数学答案一、填空题、CABBCABD 二、选择题、9. {a |a ≥2} 10. 6三、简答题、11. 解：全集U ＝{x |x ≥2或x ≤1}，∴A ∩B ＝A ＝{x |x <1，或x >3}； (∁U A )∩(∁U B )＝∁U (A ∪B )＝{2}；12. 解：若B ＝∅，则a ＋1>2a －1，则a <2，此时∁U B ＝R ，∴A ⊆∁U B ；若B ≠∅，则a ＋1≤2a －1，即a ≥2，此时∁U B ＝{x |x <a ＋1，或x >2a －1}，由于A ⊆∁U B ， 如图，则a ＋1>5，∴a >4，∴实数a 的取值范围为{a |a <2，或a >4}．13解：(1)∵f (1)＝3，即1＋m ＝3，∴m ＝2. (2)由(1)知，f (x )＝x ＋2x，其定义域是{x |x ≠0}，关于原点对称，又f (－x )＝－x ＋2－x ＝－⎝ ⎛⎭⎪⎫x ＋2x ＝－f (x )，所以此函数是奇函数． 14.错误！未找到引用源。

2021高中高一自主招生数学试题1、已知，2a a a a =÷，求a 的值2、已知，x 、y 均为正数，且511=+++yx y x ， 求y x +的最值3、设正数a 、b 满足111=+b a ，求aba b a 25++的最小值4、已知，122=+y x ，求22122-+-++-y x xy x x 的值5、如图，ABCD 为正方形，DE=5，EF=3， DF=4，求正方形的面积6、若5433=+y x ，求y x +的最大值7、若0=++c b a ，求abc c ac b b bc a a +++++222222222的值8、已知正数a 、b 满足14522=-+b ab a ，则22812b ab a -+的最小值是多少9、如图，在矩形ABCD 中，AB=3 ，AE=1， P 是AB 上一动点，EP EF ⊥，G 为PF 的中点，求点G 运动路径的长度10、如图，在ABC ∆中，090=∠ACB ，060=∠B ,CB=2 , D 为AB 上一动点，则2CD+AD 的最小值是多少11、如图，在矩形ABCD 中，AB=20， BC=10，若AC 、 AB 上各取一点M 、N ，使BM+MN 的值最小，求这个最小值。

12、如图，已知平行四边形ABCD ，a AB =，b BC =（b a >） P 为AB 边上的一动点，直线DP 交CB 延长线于Q ，求AP+BQ 的最小值13、等腰直角三角形ABC 中，090=∠ACB ,030=∠CAD ,AD ＝ AC ，则∠DBC= ．14、如图，在四边形ABCD 中，AD=DC=1 ,090=∠=∠DCB DAB ,BC 、AD 的延长线交于P ，求PAB S AB ∆⋅的最大值15、如图，求∠DAC 的度数16、如图，已知正方形ABCD 的边长为1，求阴影部分的面积17、自然数n 使得n 222118++是一个完全平方数，求n18、解方程：2213+=-+x x x19、已知1=xyz ，2=++z y x ，3222=++z y x ，求111111-++-++-+y xz x yz z xy 的值20、ABD ∆是等边三角形，在ABC ∆中，a BC = b CA = 问：当ACB ∠为何值时，CD 两点间的距离最大，最大值是多少21、如图，正方形ABCD 的对角线交于点O ，以AD 为边向外作ADE Rt ∆，090=∠AED ，连OE ，DE=6，OE=28，求AE 的长。

一、选择题6 3 横峰中学高一自招班数学试卷答案 1. C 2.B 3.D 4.B 5.B 6. A 7.B 8.B 9.C 10.C 11.B 12.A二、填空题13. 9 14.15. 16. 2三、解答题 17.解：（1） 角α为第一象限角，且sin α=5 ，5 ∴ cos α=- 3 - 31 - sin 2α==2 5 ，5∴tanα=sinα=1.cosα 21 - (5) 253+ 23sinα+ 2 cosα=3 tanα+ 2 =2（2）原式 == 7 .sinαn n tan α1218. 解：因为数列{a n }是各项均为正数的等比数列，a 3 = 2a 2 +16 ， a 1 = 2 ， 所以令数列{a }的公比为q ， a = a q 2 =2q 2， a = a q = 2q ， n 3 1 2 1所以 2q 2 = 4q +16 ，解得 q = -2 (舍去)或 4 ，所以数列{a }是首项为 2 、公比为 4 的等比数列， a = 2 ⨯ 4n -1 = 22n -1 ．(2)因为b n = log 2 a n ，所以b n = 2n -1， b n +1 = 2n +1， b n +1 - b n = 2 ，所以数列{b n }是首项为1、公差为 2 的等差数列， S n2=1+2n-1´n=n219.解：（1）连结BD交AC 于F ，连结EF．因为底面ABCD 是矩形，所以F 为BD 中点．又因为E 为PB 中点，所以PD / / EF ．因为PD ⊄平面ACE ，EF ⊂平面ACE ，所以PD / / 平面ACE ．（2）取CD 的中点 M ，连结 PM ，因为 PC =PD =点，所以PM ⊥CD ，且PM = 1，因为平面PCD ⊥平面ABCD ，PM ⊂平面PCD ，2，CD = AB = 2 ， M 是CD 的中平面 PCD ∩平面 ABCD = CD ， 所以 PM ⊥ 平面 ABCD ， 因为 E 为 PB 中点，所以V = 1 V=1⨯1⨯1⨯ 2⨯1⨯1 =1．E -ABC 2所以三棱锥E -ABC C 的体积为1．6P ABC2 3 2 620.解：（1）∵2c⋅sin B=3a⋅tan A=3a⋅sin A，cos A∴2c ⋅ sin B ⋅ cos A = 3a ⋅ sin A ，b2 +c2 -a2 2∴2c ⋅b⋅cos A = 3a ⋅a ，∴2cb ⋅= 3a ，2bc∴b2 +c2 = 4a2 ，∴b2 c2 a2= 4 ；（2）a = 1时，b2 +c2 = 4a2 = 4 ，b2 +c2 -a2 3∵cos A ==且2bc ≤b2 +c2 = 4 ，2bc 2bc∴cos A ≥3，∴当角A 最大时，cos A =3，4此时sin A⎧b2 +c2 =⎨⎩b =c24=7，4⇒b =c =，∴S =1bc ⋅ sin A =1⨯ 2 ⨯2 ⨯7=7.ABC2 2 4 421.解：（1）由题意知，3OC =OA + 2OB，即2(OC-OB)=OA-OC，所以2BC =CA，即.uuurACuur =2CB（2）易知OA = (1, cos x) ，OB = (1+ cos x, cos x) ，AB = (cos x, 0) ，则uuuv 2，u u r ，OC = (1+cos x, c os x) 32 14 g ( ) 1 AB = cos x所以 f (x ) = cos 2 x - 2m cos x +1 ，令t = cos x ，则 g (t ) = t 2 - 2mt +1， t ∈[1,1]，其对称轴方程是t = m . 2当 m ≤ 3 时， g (t ) 的最大值为 g (1) = 1- 2m +1 = 3，解得 m = - 1； 4 2 当m > 3 时， g (t ) 的最大值为 1 = 1 - m +1 = 3，解得m = - 7 （舍去）. 4 2 4 4 综上可知，实数 m 的值为- 1 .222.解：（1）根据题意，圆O : x 2 + y 2 = r 2(r > 0) 的圆心为（0，0），半径为 r ， 则圆心到直线 l 的距离 d == ， 1+1 2若直线l : x + y -1 = 0截圆O : x 2 + y 2 = r 2(r > 0) 所得的弦长为 ， 则有 2 r 2 - 1 214 = ，解可得 r = 2 ，则圆的方程为 x 2 + y 2 = 4 ；（2）直线 l 1的方程为(1+ 2m )x + (m -1) y - 3m = 0，即(x - y ) + m (2x + y - 3) = 0， ⎧ x - y = 0 ⎧x = 1 则有 ⎨2x + y - 3 = 0 ，解得⎨y = 1，即 P 的坐标为（1，1）， ⎩ ⎩点 M , N 在圆O 上，且 PM ⊥ PN ， Q 为线段 MN 的中点，则| MN |= 2 | PQ | ， 设 M N 的中点为 Q （x ，y ），则OM 2 = OQ 2 + MQ 2 = OQ 2 + PQ 2 ，即 4 = x 2 + y 2 + (x -1)2 + ( y -1)2 ，⎛ 1 ⎫2 ⎛ 1 ⎫2 3化简可得： x - 2 ⎪ + y - 2 ⎪=即为点 Q 的轨迹方程.2⎝⎭⎝⎭。