圆的切线的判定定理和性质定理

1．切线的性质 (1)性质定理：圆的切线垂直于经 过 切点的半径． 如图，已知AB切⊙O于A点，则 OA ⊥AB.
(2)推论1：经过圆心且 垂直于切线 的直线必经过切点．
(3)推论2：经过切点且 垂直于切线 的直线必经过圆心．
2．圆的切线的判定方法 (1)定义：和圆只有一个公共点的直线是圆的切线．
4.
如图，△ABC 内接于⊙O，点 D 在 OC 的延长线上，sin B 1 ＝ ，∠D＝30° . 2 (1)求证：AD 是⊙O 的切线． (2)若 AC＝6，求 AD 的长．
解：(1)证明：如图，连接 OA， 1 ∵sin B＝ ，∴∠B＝30° ， 2 ∵∠AOC＝2∠B，∴∠AOC＝60° ， ∵∠D＝30° ， ∴∠OAD＝180° －∠D－∠AOC＝90° ， ∴AD 是⊙O 的切线． (2)∵OA＝OC，∠AOC＝60° ， ∴△AOC 是等边三角形，∴OA＝AC＝6， ∵∠OAD＝90° ，∠D＝30° ， ∴AD＝ 3AO＝6 3.
在△OEC 中，因为∠EOC＝∠ECO＝30° ， ∴OE＝EC， 在△BOE 中，因为∠BOE＝90° ，∠EBO＝30° . ∴BE＝2OE＝2EC， CE CD 1 ∴BE＝DA＝ ， 2 ∴AB∥OD，∴∠ABO＝90° ， 故 AB 是△BCD 的外接圆的切线．
要证明某直线是圆的切线，主要是运用切线的判
6. 如图，正方形ABCD是⊙O的内接正方形，延长BA
到 E，使AE＝AB，连接ED.
(1)求证：直线ED是⊙O的切线； (2)连接EO交AD于点F，求证： EF＝2FO.
解：(1)证明：连接 OD. ∵四边形 ABCD 为正方形， AE＝AB， ∴AE＝AB＝AD， ∠EAD＝∠DAB＝90° . ∴∠EDA＝45° ，∠ODA＝45° . ∴∠ODE＝∠ADE＋∠ODA＝90° . ∴直线 ED 是⊙O 的切线． (2)作 OM⊥AB 于 M. ∵O 为正方形的中心，∴M 为 AB 的中点． ∴AE＝AB＝2AM，AF∥OM. EF AE ∴FO＝AM＝2，∴EF＝2FO.

A
O
B
D
练习3 若Rt△ABC内接于⊙O,∠A=30°. 延长斜边AB到D，使BD等于⊙O的半径, 求证：DC是⊙O的切线.
分析:如图
C
300600
. A
300 1200 600 600
O
B
D
练习1.如图A是⊙O外的一点，AO的延长线交 ⊙O于C，直线AB经过⊙O上一点B，且AB＝BC， ∠C＝30°. 求证：直线AB是⊙O的切线.
证明：连结OB,
∵OB=OC,AB=BC,∠C=30°
B
∴∠OBC=∠C=∠A=30° ∴∠AOB=∠C+∠OBC=60°
C O
A
∴∠ABO=180°－(∠AOB+∠A)
O
l
根据作图,直线l是⊙O切线满足两个条件： A B
1.经过半O的半径 OA⊥l于A
l是⊙O的切线.
定理说明：在此定理中，题设是“经过半径的外端” 和“垂直于这条半径”，结论为“直线是圆的切 线”， 两个条件缺一不可，否则就不是圆的切线. 下面两个反例说明只满足其中一个条件的直线不是圆的切线：
例２ 如图，AB是⊙O的直径, C为⊙O上一点， AD和过点C的切线互相垂直，垂足为D. 求证： AC平分∠DAB．
证明：连接OC．
∵CD 是⊙O的切线， ∴OC⊥CD.
D C
又∵AD⊥CD , ∴OC//AD. A
∴∠ACO＝ ∠CAD .
O
B
又∵OC=OD, ∴∠CAO＝ ∠ACO
∴∠CAD＝ ∠CAO , 故AC平分∠DAB．
O.
A
l
O.
A
l
B
３．应用：
例１ 如图，AB是⊙O的直径,⊙O过BC的中点D，

经过半径外端且垂直这条半径
是圆的切线
5、常用的添加辅助线的方法
（1）直线与圆的公共点已知时，作出过公共点的 半径，再证半径垂直于该直线。 有切点，连半径，证垂直 （2）直线与圆的公共点不确定时，过圆心作直线 的垂线段，再证明这条垂线段为圆的半径 无切点，作垂直，证半径
切线的性质
如图，⊙O的切线PC交直径AB的延长线于点P，C为切点， 若∠P＝30°，⊙O的半径为1，则PB的长为_______
无交点，作垂直，证半径
例：如图 ，已知：O 为 BAC 角平分线上一点，
OD AB 于 D ，以 O 为圆心， 为半径作圆。
求证：AC 是⊙ O 的切线。
E
数学解答题P7 数学解答题P9
P9《数学解答题》
切线的性质
P9《数学解答题》
切线的性质
P9《数学解答题》
切线的性质
切线的性质
垂直 于经过切点的半径． 定理：圆的切线________ 技巧：圆心与切点的连线是常用的辅助线．
垂直 于这条半径的直线是圆 定理： 经过半径的外端并且________ 的切线． 证圆的切线技巧： (1)如果直线与圆有交点，连接圆心与交点的半径，证明直 线与该半径垂直，即“有交点，作半径，证垂直”．
(2)如果直线与圆没有明确的交点， 则过圆心作该直线的垂 线段，证明垂线段等于半径，即“无交点，作垂直，证半径”．
切线的判定
作业：《数学解答题》 P7-10第一问
专题复习 与圆的切线有关的证明
1、圆的切线性质定理
圆的切线垂直于经过切点的半径．
2、辅助线： 连接圆心与切点
连半径，得垂直
半径与切线垂直
3、切线判定
定理:经过半径的外端并且垂直于这条半径的 直线是圆的切线。

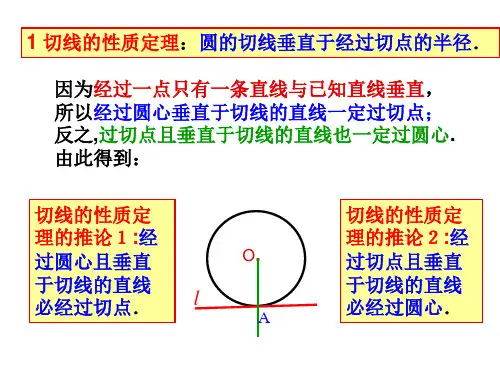
切线证明法切线的性质定理： 圆的切线垂直于经过切点的半径切线的性质定理的推论１: 经过圆心且垂直于切线的直线必经过切点． 切线的性质定理的推论２: 经过切点且垂直于切线的直线必经过圆心 切线的判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线．切线长定理: 从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。

一、要证明某直线是圆的切线，如果已知直线过圆上的某一个点，那么作出过这一点的半径，证明直线垂直于半径．【例1】如图1，已知AB 为⊙O 的直径，点D 在AB 的延长线上，BD ＝OB ,点C 在圆上，∠CAB ＝30º．求证:DC 是⊙O 的切线．思路:要想证明DC 是⊙O 的切线，只要我们连接OC ，证明∠OCD ＝90º即可． 证明：连接OC ，BC ．∵AB 为⊙O 的直径，∴∠ACB ＝90º．∵∠CAB ＝30º，∴BC ＝21AB ＝OB ．∵BD ＝OB ，∴BC ＝21OD ．∴∠OCD ＝90º．∴DC 是⊙O 的切线．【评析】一定要分清圆的切线的判定定理的条件与结论，特别要注意“经过半径的外端”和“垂直于这条半径”这两个条件缺一不可，否则就不是圆的切线．【例2】如图2，已知AB 为⊙O 的直径,过点B 作⊙O 的切线BC ,连接OC ,弦AD ∥OC ．求证：CD 是⊙O 的切线．思路：本题中既有圆的切线是已知条件，又证明另一条直线是圆的切线．也就是既要注意运用圆的切线的性质定理，又要运用圆的切线的判定定理．欲证明CD 是⊙O 的切线，只要证明∠ODC ＝90º即可．图1图2证明：连接OD ．∵OC ∥AD ，∴∠1＝∠3，∠2＝∠4． ∵OA ＝OD ，∴∠1＝∠2．∴∠3＝∠4． 又∵OB ＝OD ，OC ＝OC ，∴△OBC ≌△ODC ．∴∠OBC ＝∠ODC ．∵BC 是⊙O 的切线，∴∠OBC ＝90º．∴∠ODC ＝90º． ∴DC 是⊙O 的切线．【例3】如图2,已知AB 为⊙O 的直径,C 为⊙O 上一点，AD 和过C 点的切线互相垂直，垂足为D ．求证:AC 平分∠DAB ．思路：利用圆的切线的性质--与圆的切线垂直于过切点的半径．证明：连接OC ．∵CD 是⊙O 的切线，∴OC ⊥CD ．∵AD ⊥CD ，∴OC ∥AD ．∴∠1＝∠2． ∵OC ＝OA ，∴∠1＝∠3．∴∠2＝∠3． ∴AC 平分∠DAB ．【评析】已知一条直线是某圆的切线时,切线的位置一般是确定的．在解决有关圆的切线问题时，辅助线常常是连接圆心与切点，得到半径，那么半径垂直切线．【例4】 如图1,B 、C 是⊙O 上的点，线段AB 经过圆心O ，连接AC 、BC ，过点C 作CD ⊥AB 于D ,∠ACD =2∠B ．AC 是⊙O 的切线吗？为什么？解：AC 是⊙O 的切线． 理由：连接OC , ∵OC =OB ， ∴∠OCB =∠B ．图3 OABCD2 31∵∠COD是△BOC的外角,∴∠COD=∠OCB+∠B=2∠B．∵∠ACD=2∠B，∴∠ACD=∠COD．∵CD⊥AB于D,∴∠DCO+∠COD=90°．∴∠DCO+∠ACD=90°．即OC⊥AC．∵C为⊙O上的点，∴AC是⊙O的切线．【例5】如图2,已知⊙Ｏ是△ABC的外接圆，AB是⊙Ｏ的直径,D是AB的延长线上的一点，AE⊥DC交DC的延长线于点E，且AC平分∠EAB．求证：DE是⊙O的切线．证明:连接OC,则OA=OC，∴∠CAO=∠ACO，∵AC平分∠EAB，∴∠EAC=∠CAO=∠ACＯ,∴AE∥CO,又AE⊥DE，∴CO⊥DE，∴DE是⊙O的切线．二、直线与圆的公共点未知时须通过圆心作已知直线的垂直线段，证明此垂线段的长等于半径【例6】如图3，AB=AC，OB=OC，⊙O与AB边相切于点D．证明：连接OD，作OE⊥AC，垂足为E．∵AB=AC，OB=OC．∴AO为∠BAC角平分线，∠DAO=∠EAO∵⊙O与AB相切于点D，∴∠BDO=∠CEO=90°．∵AO=AO∴△ADO≌△AEO，所以OE=OD．∵OD是⊙O的半径,∴OE是⊙O的半径．∴⊙O与AC边相切．【例7】如图,在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于E，B为切点的切线交OD延长线于F.求证：EF与⊙O相切.证明：连结OE,AD。

线段，再证明这条垂线段等于圆的半径。（作垂直， 证半径）
1、知识：切线的判定定理．着重分析了定理成立 的条件，在应用定理时，注重两个条件缺一不 可． 2、判定一条直线是圆的切线的三种方法说明：其 中(2)和(3)本质相同，只是表达形式不同．解题 时，灵活选用其中之一．
22
思考？如图：如果L是⊙O 的切线,切点为A,那么 半径OA与直线L是不 是一定垂直呢? 一定垂直
A
O
B
31
3、如图AB是⊙O的直径.AE是弦, EF是⊙O 的切线,E是切点,AF⊥EF,垂足为F,AE平分 ∠FAB吗?
F E
A
．
O
B
A
32
4、已知，如图AB是⊙O的直径，点P在 BA的延长线上，PD切⊙O于点C， BD⊥PD,垂足为D，连接BC。 (1)求证BC平分∠PBD （2） BC2AB•BD
A、600
B、1200
B
C、600或1200
O
D、1400或600 P
A
C
41
则过圆心作直线的垂线段,再证垂线段长等于半
径长.简记为：无交点,作垂直,证半径.
16
1、如图,△ABC中,AB=AC,AO⊥BC于O，
OE⊥AC于E,以O为圆心,OE为半径作⊙O.
求证：AB是⊙O的切线.
A
F
E
B
O
C
17
2、如图,AB是⊙O的直径,点D在AB的延长 线上,BD=OB,点C在⊙O上, ∠CAB=30°.
求证:AC与⊙O相切.
A
E D
B
O
C
36
3.AB是⊙O的直径,BC是⊙O的切线,切点为B,OC 平行于弦AD. 求证:DC是⊙O的切线.

故 AC＝2AD.
【名师点评】 (1)圆的圆心；②经过切点；③垂直于切 线．用其中的某两点作条件，便能推出第三点．
(2)若题目条件中有圆的切线，可考虑连接圆心和切点，则得 垂直关系．
【名师点评】 (1)判断圆的切线的常用方法： ①和圆只有一个公共点的直线是圆的切线； ②到圆心距离等于半径的直线是圆的切线； ③过圆的半径的外端且与半径垂直的直线是圆的切线． (2)判断一条直线是圆的切线时，常用辅助线的作法： ①如果已知这条直线与圆有公共点，则连接圆心与这个公共 点，设法证明连接所得到的半径与这条直线垂直，简记为“连 半径，证垂直”； ②若题目未说明这条直线与圆有公共点，则过圆心作这条直
考点突破
考点一 圆的切线的判定 例1 如图所示，在△ABC 中，已知 AB＝AC，以 AB 为直径 的⊙O 交 BC 于点 D，DE⊥AC 于点 E. 求证：DE 是⊙O 的切线．
【证明】 连接 OD 和 AD，如图所示． ∵AB 是⊙O 的直径，∴AD⊥BC. 又∵AB＝AC，∴BD＝CD. ∵AO＝OB，∴OD∥AC. ∵DE⊥AC，∴DE⊥OD， ∴DE 是⊙O 的切线．
线的垂线，得垂线段，再证明这条垂线段的长等于半径，简
记“作垂直，证半径”．
考点二 圆的切线的性质 例2 如图，AB 和 BC 分别与圆 O 相切于点 D，C，AC 经过圆 心 O，且 BC＝2OC.求证：AC＝2AD.
【证明】 连接 OD.因为 AB 和 BC 分别与圆 O 相切于点 D，C， 所以∠ADO＝∠ACB＝90°. 又因为∠A＝∠A， 所以 Rt△ADO∽Rt△ACB. 所以OBCD＝AACD. 又 BC＝2OC＝2OD，
圆的切线的性质及判定定理
1．直线与圆的位置关系
直线与圆有两___个_公共点，称直线与圆相交；直线与圆只有一__个__

【典例训练】
1.在Rt△ABC中，∠C=90°，AC=3 cB的关系为( )
(A)相切
(B)相离
(C)相交
(D)无法判断
2.如图所示，CB为⊙O的直径，P是CB的延
长线上一点，且OB=BP，∠AOC=120°，
则PA与⊙O的位置关系是_____.
圆的切线的性质
圆的切线的性质 (1)已知一条直线是圆的切线时,常作出过切点的半径,则该半 径垂直于切线,从而出现了直角. (2)从圆外一点引圆的两条切线,这点与圆心的连线平分这两条 切线的夹角,这点到切点的切线长相等. (3)连接圆的两条平行切线的切点的线段是圆的直径.
【典例训练】 1.如图所示，DB，DC是⊙O的两条切线，A是圆上一点，已知 ∠D=46°，则∠A=_____.
DO AD
AD
2.如图，已知EB是半圆O的直径，A是BE延长线上的一点，AC是 半圆O的切线，D为切点，BC⊥AC于C，若BC=6，AC=8，则 AE=_______.
【解析】1.如图所示，连接OB，OC，
则OB⊥BD，OC⊥CD，
则∠DBO+∠DCO=90°+90°=180°，
则四边形OBDC内接于一个圆，
则有∠BOC=180°-∠D=180°-46°=134°，
【解析】连接OC，∵OA=OB,AC=CB,OC=OC, ∴△OAC≌△OBC, ∴∠OCA=∠OCB=90°, ∴直线AB与⊙O相切. 答案：相切
1.圆的切线的其他相关性质 (1)切线和圆只有一个公共点; (2)切线和圆心的距离等于圆的半径; (3)过圆心且过切点的直线与过该点的切线垂直.
2.切线的判定定理 在切线的判定定理中要分清定理的题设和结论，“经过半径外 端”和“垂直于这条半径”这两个条件缺一不可，否则就不是 圆的切线，如图①②中的例子就不同时满足这两个条件，所以 都不是圆的切线.

判定定理1
直线与圆有唯一公共点时，直线与圆 相切。通过证明直线与圆的交点唯一 ，可以判定直线与圆相切。
判定定理2
圆心到直线的距离等于半径时，直线 与圆相切。利用点到直线的距离公式 ，可以计算出圆心到直线的距离，进 而判定直线与圆的位置关系。
结合多种方法解决复杂问题
在解决复杂问题时，可以结合切线性质定理和判定定理，以及其他数学知识如三角函数、相似三角形等，建立方程或不等式 组，逐步求解。
VS
利用直线与圆的公共点的个数来判断。 若直线与圆只有一个公共点，则该直 线为切线；若有两个公共点，则为割 线。
04 判定定理三：切线长定理
从圆外一点引圆的两条切线
切线的定义
从圆外一点引到圆上的线段 ，如果它的端点在圆上，则 这条线段叫做圆的切线。
切线的性质
圆的切线垂直于过切点的半 径。
切线长的定义
从圆外一点引圆的两条切线 ，它们的切线长分别是从该 点到切点的线段的长度。
它们的切线长相等
切线长定理的表述
从圆外一点引圆的两条切线，它们的切线长相等。
切线长定理的证明
由于两条切线都垂直于过切点的半径，因此它们与半径构成的直角三角形全等，从而得出切线长相等。
圆心和这一点的连线平分两条切线的夹角
01
公共点的存在表明割线与圆有交点， 是判定割线与圆位置关系的重要依据。
割线长度大于切线长度
从圆外一点引两条线，一条是切线，一条是割线，则切线长小于割线长。
切线长是指从圆外一点引到圆上的切线段的长度，而割线长则是指从同一点引到圆上的割线段的长度 。
割线与圆相切判定方法
利用圆心到直线的距离等于半径来判 断。若圆心到直线的距离等于半径， 则该直线为切线；若距离大于半径， 则为割线。

切线的判定和性质
切线的性质与判定
1.主要性质
（1）切线和圆只有一个公共点；
（2）切线和圆心的距离等于圆的半径；
（3）切线垂直于经过切点的半径；
（4）经过圆心垂直于切线的直线必过切点；
（5）经过切点垂直于切线的直线必过圆心；
（6）从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

其中（1）是由切线的定义得到的，（2）是由直线和圆的位置关系定理得到的，（6）是由相似三角形推得的，也就是切割线定理。

2.判定
切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。

圆的切线垂直于这个圆过切点的半径。

证明: 连接OD， BD CD,OA OB OD是ABC的中位线, OD // AC, AED EDO 180 0, AED 900 EDO 900
又 D在圆周上 DE是圆O的切线.
C
D E
B
O
A
例2 如图，AB为圆O的直径，C为圆O上一点，AD和过点C 的切线互相垂直，垂足为D. 求证：AC平分DAB.
证明: 连接OC， CD是圆O的切线， OC CD,
又 AD CD, OC // AD,
CAD ACO OA OC
ACO CAO
CAD CAO. 故AC平分DAB.
D C
B
A
O
小结
1、圆的切线的性质定理 2、圆的切线的判定定理
M A
因此，l与OA一定垂直.
l
O
切线的性质定理
圆的切线垂直于经过切点的半径． A
推论１
l
O
经过圆心且垂直于切线的直线必经过切点．
推论 2
经过切点且垂直于切线的直线必经过圆心．
已知：如图，点 A是圆O与直线l的公共点且 l OA. 求证：直线 l是圆O的切线.
证明：在直线l上任取异于点A的点B，连接OB，
则有，ABO是直角三角形，
OB OA. 因此，点B在圆外.
由点B的任意性，可知
B A
直线与圆只有一个交点， l
因此，l是圆的切线.
O
切线的判定定理
经过半径的外端并且垂直于这条半径的 直线是圆的切线．
例1 如图，AB是圆O的直径，圆 O过BC的中点D，DE AC . 求证： DE 是圆O的切线.
知识回顾
直线与圆的位置关系：
相交 相切 相离
有两个公共点 有一个公共点 没有公共点

切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线几何语言：∵l⊥O A，点 A 在⊙O 上∴直线l 是⊙O 的切线（切线判定定理）切线的性质定理圆的切线垂直于经过切点的半径几何语言：∵OA 是⊙O 的半径，直线l 切⊙O 于点 A∴l⊥O A（切线性质定理）推论 1 经过圆心且垂直于切线的直径必经过切点推论 2 经过切点且垂直于切线的直线必经过圆心切线长定理从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角几何语言：∵直线PA 、PB 分别切⊙O 于A、B 两点∴PA=PB ，∠APO= ∠BPO （切线长定理）证明：连结OA 、OB∵直线PA 、PB 分别切⊙ O 于A、B 两点∴OA ⊥AP 、OB ⊥PB∴∠OAP= ∠OBP=90 °弦切角（即图中 ∠ ACD) 等于它所夹的弧 弧的读数的一半等于完整，图中没有连结 1/2 所夹的弧的圆心角 OC] ( 弧 AC) 对的圆周角等于所夹的 [注，由于网上找得的图不是很几何语言： ∵∠ ACD 所夹的是弧 AC∴∠ ACD= ∠ABC=1/2 ∠ COA=1/2 弧 AC 的度数 ( 弦切角定理）推论 如果两个弦切角所夹的弧相等，那么这两个弦切角也相等几何语言： ∵∠ 1 所夹的是弧 MN ， ∠ 2 所夹的是 PQ ，弧 MN = 弧 PQ∴∠ 1= ∠ 2证明：作 AD ⊥EC∵∠ ADC=90 °∴∠ ACD+ ∠ CAD=90 °在△OPA 和△OPB 中：∠OAP= ∠OBPOP=OPOA=OB=r∴△OPA ≌△OPB （ HL ）∴PA=PB ，∠APO= ∠BPO弦切角概念顶点在圆上，一边和圆相交、另一边和圆相切的角叫做弦切角．它是继圆心角、圆周角之后第三种与圆有关的角．这种角必须满足三个条件：（1））顶点在圆上，即角的顶点是圆的一条切线的切点； （2））角的一边和圆相交，即角的一边是过切点的一条弦所在的射线； （3） ）角的另一边和圆相切，即角的另一边是切线上以切点为端点的一条射线。

切线的三个性质
一、切线的性质与切线的判定
1.切线性质：
①圆的切线垂直于经过切点的半径。

②经过圆心且垂直于切线的直线必经过切点。

③经过切点且垂直于切线的直线必经过圆心。

2.切线的判定：经过半径的外端且垂直于这条半径的直线是圆的切线。

二、切线的判定定理与切线的性质定理的区别
切线的判定定理是在未知相切而要证明相切的情况下使用；切线的性质定理是在已知相切而要推得一些其他结论时使用，两者在使用时不要混淆。

三、常用辅助线
①判定切线时“连圆心和直线与圆的公点”或“过圆心作这条直线的垂线”；
②有切线时，常常“遇到切点连圆心得半径”。

O l A
切线必须同时满足两条：①经过半径 外端；②垂直于这条半径．
如图，如果直线l是⊙O的切线，切点为A， 那么半径OA与直线l是不是一定垂直呢？
∵ l是⊙O的切线，切点为A
O
l A
∴ l ⊥OA
切线的性质定理：圆的
切线垂直于过切点的半径。
数学语言：
O l A
∵ l是⊙O的切线，切点为A
∴ l ⊥OA
A P
C B
O
如图，已知：在△ABC中，∠B＝90°，O是AB上一 点，以O为圆心，OB为半径的圆交AB于点E，切AC 与点D。求证：DE∥OC
C 证明：连接ＢＤ． ∵∠ＡＢＣ＝９０°，ＯＢ为⊙Ｏ的半径 ∴ＣＢ是⊙Ｏ的切线 ∵ＡC是⊙Ｏ的切线，Ｄ是切点 ∴ＣＤ＝ＣＢ，∠１＝∠２ ∴ＯＣ⊥ＢＤ ∵ＢＥ是⊙Ｏ的直径 ∴∠ＢＤＥ＝９０°，即ＤＥ⊥ＢＤ ∴ＤＥ∥ＯＣ A E D O
勾股（逆）定理 切 线 判 定
∴C(-2,0), P(0,-4) 数据“放入”图中。猜想直线 又∵ D(0,1) OC=2, OP=4 ,OD=1, DP=5 PC 与⊙ D∴ 相切。怎么证？联 又∵在Rt△COD中, CD2=OC2+OD2=4+1=5 想证明切线的两种方法。点 在Rt△COP中, CP2=OC2+OP2=4+16=20 C 在圆上，即证：∠ DCP=90° 在△ CPD中, CD2+CP2=5+20=25, DP2=25 2 2 2 ∴ CD +CP =DP 利用勾股及逆定理可得。
即：△CDP为直角三角形,且∠DCP=90° ∴PC为⊙D的切线.
已知,如图,D(0,1),⊙D交y轴于A、B两点,交x轴负 半轴于C点,过C点的直线:y=－2x－4与y轴交于P. ⑵判断在直线PC上是否存在点E，使得S△EOC= 4S△CDO,若存在，求出点E的坐标；若不存在， 请说明理由.

切线长定理的拓展
A
D
OHຫໍສະໝຸດ CPB（1）写出图中所有的垂直关系 （2）图中有哪些线段相等(除半径 外)、弧相等？
o．
．
o．
三角形外接圆
C
三角形内切圆
C
． o
A B B
． o
A
外接圆圆心：三角形三边 垂直平分线的交点。
外接圆的半径：交点到三 角形任意一个定点的距离。
内切圆圆心：三角形三个 内角平分线的交点。 内切圆的半径：交点到三 角形任意一边的垂直距离。
例2 已知：如图, △ABC的内切圆⊙O与 BC 、CA、 AB 分别相交于点D 、 E 、 F ，且AB＝9厘米，BC ＝14厘米,CA ＝ 13厘米,求AF、BD、CE的长。
A E F B D O C
小结：
（1）切线长定理。 （2）连接圆心和切点是我 们解决切线长定理相关问题 时常用的辅助线。
∵PA、PB是⊙o的两条切线，
关键是作辅助 ∴OA⊥AP，OB⊥BP 线~ 根据你的直观判断，猜想图中PA是否等于PB？∠1与∠2又 又OA=OB，OP=OP， 有什么关系？
∴Rt△AOP≌Rt△BOP（HL） ∴PA=PB，∠1=∠2
⌒
P
A
O
P
B
• 切线长定理：
•
从圆外一点引圆的两条切线，它们的切线 长相等，这一点和圆心的连线平分两条切 线的夹角。
复习：
切线的判定：
切线的性质：
问题：
过平面内的一点作圆的切 线，可以作出几条切线？
A
O
P
B
过圆外一点作圆的切线，这点 和切点之间的线段的长，叫做这点 到圆的切线长。
A
O
P

圆的切线
圆切线具有如下性质：
(1)切线与圆只有一个公共点；
(2)切线与圆心的距离等于圆的半径；
(3)切线垂直于过切点的半径；
(4)经过圆心垂直于切线的直线必过切点；
(5)经过切点垂直于切线的直线必过圆心．
从上述5条性质知道：性质(1)是切线的定义；性质(2)是切线判定方法的逆定理；性质(3)、(4)、(5)是切线性质定理及其推论，其中性质(2)、(3)应用较多．
在应用切线性质定理时，如果只有切线，没有半径，要添加辅助线——就是连接过切点的半径，则此半径必垂直于切线．
应用切线的性质能解决几何计算与证明中的有关问题．
(1)利用切线性质计算线段的长度
例1：如图，已知：AB是⊙O的直径，P为延长线上的一点，PC切⊙O于C，CD⊥AB于D，又PC=4，⊙O的半径为3．求：OD的长．
例2：如图，已知：AB是⊙O的直径，CD切⊙O于C，AE⊥CD于E，BC的延长线与AE 的延长线交于F，且AF=BF．求：∠A的度数．
例4：如图，已知：AB是⊙O直径，CO⊥AB，CD切⊙O于D，AD交CO于E．求证：CD=CE．
例5：如图，已知：△ABC中，AB=AC，以AB为直径作⊙O，交BC于D，DE切⊙O于D，交AC于E．求证：DE⊥AC．。

提示：连接AO，DO，作 OE⊥AC 于点E．
E
总结：看到切线，就要连接切点和圆心，利用切线性质．
AB 是 ⊙O 的直径，AE 平分∠BAC 交 ⊙O 于点E，过点 E 作⊙O 的切线交AC 于点D，试判断△AED 的形状，并说明理 由提．示：连接OE．
答案：△AED是直角三角形． 总结：看到切线，就要连接切点和圆心，利用切线性质．
判断一条直线是圆的切线，你现在会有多少种方法? 有以下三种方法： 1．定义法：和圆有且只有一个公共点的直线是圆的切线． 2．数量法（d=r）：圆心到直线的距离等于半径的直线是圆 的切线． 3．判定定理：经过半径外端且垂直于这条半径的直线是圆的 切线．
生活中的切线
1．当你在下雨天快速转
2．砂轮打磨零件时
知识回顾 直线和圆的位置关系
相交
图形
公共点个数 公共点名称 直线名称 距离d与半径r的关系
2个 交点 割线 d＜r
相切
相离
1个 切点 切线 d=r
0个 —— —— d＞r
思考
如图，在 ⊙O 中，经过半径 OA 的外端点 A 作直线 l⊥OA， 则圆心 O 到直线 l 的距离是多少？直线 l 和 ⊙O 有什么位置关 系？
圆的切线垂直于过切点的半径．
切线的性质定理 圆的切线垂直于过切点的半径．
几何表述： ∵ l 与 ⊙O 相切于点 A ∴ OA⊥l
切线的性质定理的证明
证明切线性质定理需要用到反证法：
假设OA与 l 不垂直，
过点O 作OM⊥l，垂足为M．
M
根据垂线段最短的性质，有OM＜OA，
这说明圆心 O 到直线l的距离小于半径OA．
提示：连接OD，证明三角形全等.
补充题

∴OC⊥CD.
D C
又∵AD⊥CD,
∴OC//AD.由此得 ∠ACO=∠CAD. ∵OC=OA. ∴ ∠CAO=∠ACO. ∴ ∠CAD=∠CAO. 故AC平分∠DAB.
A O B
习题2.3
1.如图,△ABC为等腰三角形,O是底边BC的中点, ⊙O与腰AB相切于点D.
求证:AC与⊙O相切.
D
A
E
B
线的性质及它的两个推论 概括出来吗？
如果一条直线具备下列三个条件中的任意两个， 就可以推出第三个：（1）垂直于切线；（2） 过切点；（3）过圆心。
直线经过切点
切线垂直于半径
经过圆心
垂直于切线
直线经过切点 经过圆心
垂直于切线 经过圆心 直线经过切点
练一练
按图填空： (1). 如果AB是⊙O的切线， 那么 OA ⊥ AB. (2). 如果OA⊥AB，那 么AB是 ⊙O的切线
A
O
D E
.
B
F
例1 如图,AB是⊙O的直径, ⊙O过BC的中点D, DE⊥AC.求证:DE是⊙O是切线.
证明:连接OD. ∵BD=CD,OA=OB,
∴OD是△ABC的中位线, ∴OD//AC. 又∵∠DEC=90º
E D C
∴∠ODE=90º
又∵D在圆周上,
A O
B
∴DE是⊙O是切线..
例2 如图. AB为⊙O的直径,C为⊙O上一点,AD和 过C点的切线互相垂直,垂足为D. 求证:AC平分∠DAB. 证明:连接OC, ∵CD是⊙O的切线,
几何语言：∵ l 相切⊙O于Ａ, A是切点, OA是⊙O的半径 ∴l ⊥OA. 提示：切线的性质定理是证明两条直线垂直的重要根据; 作过切点的半径是常用辅助线之一.