第一章作业题答案-xy

《数学物理方法》第一章作业参考解答1. 利用复变函数导数的定义式，推导极坐标系下复变函数),(),()(ϕρϕρiv u z f +=的C-R 条件为∂∂−=∂∂∂∂=∂∂ϕρρϕρρu v vu 11 证：由于复变函数)(z f 可导，即沿任何路径，任何方式使0→∆z 时，z z f z z f ∆−∆+)()(的极限都存在且相等，因此，我们可以选择两条特殊路径，（1）沿径向，0→∆=∆ϕρi e z.ϕϕρρϕρρϕρρϕρϕρϕρρϕρρϕρϕρρi i e v i u e iv u iv u z f f −→∆∂∂+∂∂=∆−−∆++∆+=∆−∆+),(),(),(),(),(),(),(),(lim（2）沿半径为ρ的圆周，()()ϕρρρρϕϕϕϕϕ∆≈−=∆=∆∆+i i i i e i e e e zϕϕϕϕϕρϕϕρϕϕρϕρϕρϕρϕϕρϕϕρρϕρϕρϕϕρϕϕρϕρϕϕρi i i i e u i v ie iv u iv u e e iv u iv u zf f −∆→∆∂∂−∂∂=∆−−∆++∆+=−−−∆++∆+=∆−∆+1),(),(),(),(),(),()1(),(),(),(),(),(),(lim以上两式应相等，因而，ϕρρ∂∂=∂∂vu 1 ϕρρ∂∂−=∂∂u v 1 2. 已知一平面静电场的等势线族是双曲线族C xy =,求电场线族，并求此电场的复势（约定复势的实部为电势）。

如果约定复势的虚部为电势，则复势又是什么？解：0)(2=∇xy xy y x u =∴),(由C-R 条件可得C x x b x y u x b x v x b y y x v y x u y v +−=⇒−=∂∂−=′=∂∂+=⇒=∂∂=∂∂2221)()()(21),(C y x y x v +−−=)(21),(22电场线族为：（或者：由 +−=+−=∂∂+∂∂=222121),(y x d ydy xdx dy y v dx x v y x dv ，得C y x y x v +−−=)(21),(22）iC z i i C y x xy +−=+−−+=2222)(21w 复势为：若虚部为电势，则xy y x v =),(同理由C-R 条件可得Cx x A x y v x A x u x A y y x u y x v y u +=⇒=∂∂=′=∂∂+−=⇒−=∂∂−=∂∂2221)()()(21),(C y x y x u +−=)(21),(22C z ixy C y x +=++−=22221)(21w 复势为：3．讨论复变函数||)(xy iy x z f =+=在0=z 的可导性？（提示：选择沿X 轴、Y 轴和Y=aX 直线讨论）解：考虑当函数沿y=ax 趋近z=0时2)(ax z f = )1()1(||||lim )()(lim00+±=+∆−∆+=∆−∆+→∆→∆ia aia x x a x x a z z f z z f x z 可见上式是和a 有关的，不是恒定值所以该函数在z=0处不可导4.判断函数()()111)(2−++=−+=z z z z z z f 的支点，选定一个单值分支)(0z f ，计算)(0x f ？计算)(0i f −的值？ 解：可能的支点为∞−=,1,1,0z 。

3．2全集与补集学习目标 1.理解全集、补集的概念.2.准确翻译和使用补集符号和Venn图.3.会求补集，并能解决一些集合综合运算的问题．知识点一全集思考老和尚问小和尚：“如果你前进是死，后退是亡，那你怎么办？”小和尚说：“我从旁边绕过去．”在这一故事中，老和尚设定的运动方向共有哪些？小和尚设定的运动方向共有哪些？答案老和尚设定的运动方向只有2个：前进，后退．小和尚偷换了前提：运动方向可以是四面八方任意方向．梳理(1)定义：在研究某些集合时，这些集合往往是某个给定集合的子集，这个给定的集合叫作全集，全集含有我们所要研究的这些集合的全部元素．(2)记法：全集通常记作U.知识点二补集思考实数集中，除掉大于1的数，剩下哪些数？答案剩下不大于1的数，用集合表示为{x∈R|x≤1}．梳理类型一求补集例1(1)若全集U＝{x∈R|－2≤x≤2}，A＝{x∈R|－2≤x≤0}，则∁U A等于()A．{x|0<x<2} B．{x|0≤x<2}C．{x|0<x≤2} D．{x|0≤x≤2}答案 C解析∵U＝{x∈R|－2≤x≤2}，A＝{x∈R|－2≤x≤0}，∴∁U A＝{x|0<x≤2}，故选C.(2)设U＝{x|x是小于9的正整数}，A＝{1,2,3}，B＝{3，4,5,6}，求∁U A，∁U B.解根据题意可知，U＝{1,2,3,4,5,6,7,8}，所以∁U A＝{4,5,6,7,8}，∁U B＝{1,2,7,8}．(3)设全集U＝{x|x是三角形}，A＝{x|x是锐角三角形}，B＝{x|x是钝角三角形}，求A∩B，∁U(A∪B)．解根据三角形的分类可知A∩B＝∅，A∪B＝{x|x是锐角三角形或钝角三角形}，∁U(A∪B)＝{x|x是直角三角形}．反思与感悟求集合的补集，需关注两处：一是认准全集的范围；二是利用数形结合求其补集，常借助Venn图、数轴、坐标系来求解．跟踪训练1(1)设集合U＝{1,2,3,4,5}，集合A＝{1,2}，则∁U A＝________.答案{3,4,5}(2)已知集合U＝R，A＝{x|x2－x－2≥0}，则∁U A＝________.答案{x|－1<x<2}(3)已知全集U＝{(x，y)|x∈R，y∈R}，集合A＝{(x，y)|xy>0}，则∁U A＝________.答案{(x，y)|xy≤0}类型二补集性质的应用命题角度1补集性质在集合运算中的应用例2已知A＝{0,2,4,6}，∁U A＝{－1，－3,1,3}，∁U B＝{－1,0,2}，用列举法写出集合B.解∵A＝{0,2,4,6}，∁U A＝{－1，－3,1,3}，∴U＝{－3，－1,0,1,2,3,4,6}．而∁U B＝{－1,0,2}，∴B＝∁U(∁U B)＝{－3,1,3,4,6}．反思与感悟从Venn图的角度讲，A与∁U A就是圈内和圈外的问题，由于(∁U A)∩A＝v，(∁A)∪A＝U，所以可以借助圈内推知圈外，也可以反推．U跟踪训练2如图所示的V enn图中，A、B是非空集合，定义A*B表示阴影部分的集合．若A＝{x|0≤x≤2}，B＝{y|y＞1}，则A*B＝________________.答案 {x |0≤x ≤1或x ＞2}解析 A ∩B ＝{x |1<x ≤2}，A ∪B ＝{x |x ≥0}， 由图可得A *B ＝∁(A ∪B )(A ∩B )＝{x |0≤x ≤1或x ＞2}．命题角度2 补集性质在解题中的应用 例3 关于x 的方程：x 2＋ax ＋1＝0，① x 2＋2x －a ＝0，② x 2＋2ax ＋2＝0，③若三个方程至少有一个有解，求实数a 的取值范围． 解 假设三个方程均无实根，则有⎩⎪⎨⎪⎧ Δ1＝a 2－4<0，Δ2＝4＋4a <0，Δ3＝4a 2－8<0，即⎩⎪⎨⎪⎧－2<a <2，a <－1，－2<a < 2.解得－2<a <－1，∴当a ≤－2或a ≥－1时，三个方程至少有一个方程有实根， 即a 的取值范围为{a |a ≤－2或a ≥－1}．反思与感悟 运用补集思想求参数取值范围的步骤：(1)把已知的条件否定，考虑反面问题；(2)求解反面问题对应的参数的取值范围；(3)求反面问题对应的参数的取值集合的补集． 跟踪训练3 若集合A ＝{x |ax 2＋3x ＋2＝0}中至多有一个元素，求实数a 的取值范围． 解 假设集合A 中含有2个元素， 即ax 2＋3x ＋2＝0有两个不相等的实数根，则⎩⎪⎨⎪⎧a ≠0，Δ＝9－8a >0，解得a <98且a ≠0，则集合A 中含有2个元素时， 实数a 的取值范围是{a |a <98且a ≠0}．在全集U ＝R 中，集合{a |a <98且a ≠0}的补集是{a |a ≥98或a ＝0}，所以满足题意的实数a 的取值范围是{a |a ≥98或a ＝0}．类型三 集合的综合运算例4 (1)已知集合A ，B 均为全集U ＝{1,2,3,4}的子集，且∁U (A ∪B )＝{4}，B ＝{1,2}，则A ∩(∁U B )等于()A ．{3}B ．{4}C ．{3,4}D ．∅ 答案 A解析 ∵∁U (A ∪B )＝{4}， ∴A ∪B ＝{1,2,3}，又∵B ＝{1,2}，∴∁U B ＝{3,4}， A 中必有3，可以有1,2，一定没有4. ∴A ∩(∁U B )＝{3}．(2)已知集合A ＝{x |x ≤a }，B ＝{x |1≤x ≤2}，且A ∪(∁R B )＝R ，则实数a 的取值范围是________． 答案 {a |a ≥2}解析 ∵∁R B ＝{x |x <1或x >2}且A ∪(∁R B )＝R ， ∴{x |1≤x ≤2}⊆A ，∴a ≥2.反思与感悟 解决集合的混合运算时，一般先计算括号内的部分，再计算其他部分．有限集混合运算可借助Venn 图，与不等式有关的可借助数轴．跟踪训练4 (1)已知集合U ＝{x ∈N |1≤x ≤9}，A ∩B ＝{2,6}，(∁U A )∩(∁U B )＝{1,3,7}， A ∩(∁U B )＝{4,9}，则B 等于( ) A ．{1,2,3,6,7} B ．{2,5,6,8} C ．{2,4,6,9} D ．{2,4,5,6,8,9}答案 B解析 根据题意可以求得U ＝{1,2,3,4,5,6,7,8,9}，画出Venn 图(如图所示)，可得B ＝{2,5,6,8}，故选B.(2)已知集合U＝{x|x≤4}，集合A＝{x|－2<x<3}，B＝{x|－3≤x≤2}，求A∩B，(∁U A)∪B，A∩(∁U B)．解如图所示．∵A＝{x|－2<x<3}，B＝{x|－3≤x≤2}，∴∁U A＝{x|x≤－2或3≤x≤4}，∁U B＝{x|x<－3或2<x≤4}．A∩B＝{x|－2<x≤2}，∴(∁U A)∪B＝{x|x≤2或3≤x≤4}，A∩(∁U B)＝{x|2<x<3}．1．设集合U＝{1,2,3,4,5,6}，M＝{1,2,4}，则∁U M等于()A．U B．{1,3,5}C．{3,5,6} D．{2,4,6}答案 C2．已知全集U＝{1,2,3,4}，集合A＝{1,2}，B＝{2,3}，则∁U(A∪B)等于()A．{1,3,4} B．{3,4}C．{3} D．{4}答案 D3．设集合S＝{x|x>－2}，T＝{x|－4≤x≤1}，则(∁R S)∪T等于()A．{x|－2<x≤1} B．{x|x≤－4}C．{x|x≤1} D．{x|x≥1}答案 C4．设全集U＝R，则下列集合运算结果为R的是()A．Z∪∁U N B．N∩∁U NC．∁U(∁U∅) D．∁U Q答案 A5．设全集U＝M∪N＝{1,2,3,4,5}，M∩(∁U N)＝{2,4}，则N等于()A．{1,2,3} B．{1,3,5}C．{1,4,5} D．{2,3,4}答案 B1．全集与补集的互相依存关系(1)全集并非是包罗万象，含有任何元素的集合，它是对于研究问题而言的一个相对概念，它仅含有所研究问题中涉及的所有元素，如研究整数，Z就是全集，研究方程的实数解，R 就是全集．因此，全集因研究问题而异．(2)补集是集合之间的一种运算．求集合A的补集的前提是A是全集U的子集，随着所选全集的不同，得到的补集也是不同的，因此，它们是互相依存、不可分割的两个概念．(3)∁U A的数学意义包括两个方面：首先必须具备A⊆U；其次是定义∁U A＝{x|x∈U，且x∉A}，补集是集合间的运算关系．2．补集思想做题时“正难则反”策略运用的是补集思想，即已知全集U，求子集A，若直接求A困难，可先求∁U A，再由∁U(∁U A)＝A求A.课时作业一、选择题1．已知全集U＝{0,1,2,3,4}，集合A＝{1,2,3}，B＝{2,4}，则(∁U A)∪B为()A．{1,2,4} B．{2,3,4}C．{0,2,4} D．{0,2,3,4}答案 C解析∁U A＝{0,4}，所以(∁U A)∪B＝{0,2,4}，选C.2．已知A，B均为集合U＝{1,3,5,7,9}的子集，且A∩B＝{3}，(∁U B)∩A＝{9}，则A等于() A．{1,3} B．{3,7,9} C．{3,5,9} D．{3,9}答案 D解析如图，阴影部分为(∁U B)∩A，∴A＝{3,9}．3．已知全集U ＝{1,2，a 2－2a ＋3}，A ＝{1，a }，∁U A ＝{3}，则实数a 等于( ) A ．0或2 B ．0 C ．1或2 D ．2答案 D解析 由题意，知⎩⎪⎨⎪⎧a ＝2，a 2－2a ＋3＝3，则a ＝2.4．图中的阴影部分表示的集合是( )A ．A ∩(∁UB ) B ．B ∩(∁U A )C ．∁U (A ∩B )D ．∁U (A ∪B )答案 B解析 阴影部分表示集合B 与集合A 的补集的交集． 因此阴影部分所表示的集合为B ∩(∁U A )．5．已知U 为全集，集合M ，N ⊆U ，若M ∩N ＝N ，则( ) A ．∁U N ⊆∁U M B ．M ⊆∁U N C ．∁U M ⊆∁U N D ．∁U N ⊆M 答案 C解析 由M ∩N ＝N 知N ⊆M .∴∁U M ⊆∁U N .6．设全集U ＝{x ∈N |x ≥2}，集合A ＝{x ∈N |x 2≥5}，则∁U A 等于( ) A ．∅ B ．{2} C ．{5} D ．{2,5} 答案 B解析 因为A ＝{x ∈N |x ≤－5或x ≥5}， 所以∁U A ＝{x ∈N |2≤x <5}，故∁U A ＝{2}． 二、填空题7．已知全集U ＝R ，A ＝{x |x ≤0}，B ＝{x |x ≥1}，则集合∁U (A ∪B )＝______，(∁U A )∩(∁U B )＝________.答案 {x |0<x <1} {x |0<x <1}解析A∪B＝{x|x≤0或x≥1}，∁U(A∪B)＝{x|0<x<1}．∁U A＝{x|x>0}，∁U B＝{x|x<1}，∴(∁A)∩(∁U B)＝{x|0<x<1}．U8．若全集U＝{(x，y)|x∈R，y∈R}，A＝{(x，y)|x>0，y>0}，则点(－1,1)________∁U A.(填“∈”或“∉”)答案∈解析显然(－1,1)∈U，且(－1,1)∉A，∴(－1,1)∈∁U A.9．设U＝R，已知集合A＝{x|x>1}，B＝{x|x>a}，且(∁U A)∪B＝R，则实数a的取值范围是________．答案{a|a≤1}解析∁U A＝{x|x≤1}，∵(∁U A)∪B＝R，∴B⊇{x|x>1}，∴a≤1.10．若集合A＝{x|0≤x≤2}，B＝{x|x<0或x>1}，则图中阴影部分所表示的集合为________．答案{x|x≤1或x>2}解析如图，设U＝A∪B＝R，A∩B＝{x|1<x≤2}，∴阴影部分为∁U(A∩B)＝{x|x≤1或x>2}．三、解答题11．已知全集U＝R，集合A＝{x|1≤x≤2}，若B∪(∁U A)＝R，B∩(∁U A)＝{x|0<x<1或2<x<3}，求集合B.解∵A＝{x|1≤x≤2}，∴∁U A＝{x|x<1或x>2}．又B∪(∁U A)＝R，A∪(∁U A)＝R，可得A⊆B.而B∩(∁U A)＝{x|0<x<1或2<x<3}，∴{x |0<x <1或2<x <3}⊆B . 借助于数轴可得B ＝A ∪{x |0<x <1或2<x <3}＝{x |0<x <3}．12．已知U ＝R ，集合A ＝{x |x 2－x －2＝0}，B ＝{x |mx ＋1＝0}，B ∩(∁U A )＝∅，求实数m 的值．解 A ＝{－1,2}，B ∩(∁U A )＝∅等价于B ⊆A . 当m ＝0时，B ＝∅⊆A ； 当m ≠0时，B ＝{－1m}．∴－1m ＝－1或－1m ＝2，即m ＝1或m ＝－12.综上，m 的值为0,1，－12.13．设全集为R ，A ＝{x |3<x <7}，B ＝{x |4<x <10}． (1)求∁R (A ∪B )及(∁R A )∩B ；(2)若C ＝{x |a －4≤x ≤a ＋4}，且A ∩C ＝A ，求a 的取值范围． 解 (1)∵A ∪B ＝{x |3<x <10}， ∴∁R (A ∪B )＝{x |x ≤3或x ≥10}． 又∵∁R A ＝{x |x ≤3或x ≥7}， ∴(∁R A )∩B ＝{x |7≤x <10}． (2)∵A ∩C ＝A ，∴A ⊆C .∴⎩⎪⎨⎪⎧a ＋4≥7，a －4≤3⇒⎩⎨⎧a ≥3，a ≤7⇒3≤a ≤7.∴a 的取值范围为{a |3≤a ≤7}． 四、探究与拓展14.如图，已知I 是全集，A ，B ，C 是它的子集，则阴影部分所表示的集合是( )A ．(∁I A ∩B )∩C B ．(∁I B ∪A )∩C C ．(A ∩B )∩(∁I C )D ．(A ∩∁I B )∩C 答案 D解析 由题图可知阴影部分中的元素属于A ，不属于B ，属于C ，则阴影部分表示的集合是(A ∩∁I B )∩C .15．设全集U ＝{(x ，y )|x ∈R ，y ∈R }，集合M ＝{(x ，y )|y －3x －2＝1}，P ＝{(x ，y )|y ≠x ＋1}，求∁U (M ∪P )．解 集合M 表示的是直线y ＝x ＋1上除去点(2,3)的所有点，集合P 表示的是不在直线y ＝x ＋1上的所有点，显然M ∪P 表示的是平面内除去点(2,3)的所有点，故∁U (M ∪P )＝{(2,3)}．。

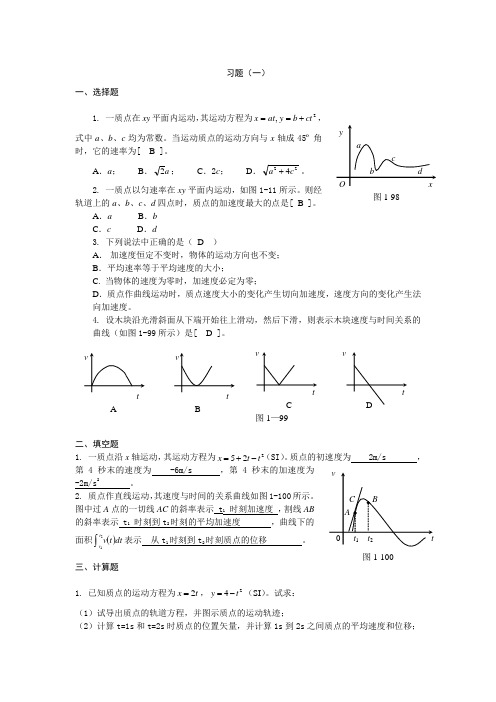
习题（一）一、选择题1. 一质点在xy 平面内运动，其运动方程为2,ct b y at x +==，式中a 、b 、c 均为常数。

当运动质点的运动方向与x 轴成45º角时，它的速率为[ B ]。

A ．a ；B ．a 2；C ．2c ；D ．224c a +。

2. 一质点以匀速率在xy 平面内运动，如图1-11所示。

则经轨道上的a 、b 、c 、d 四点时，质点的加速度最大的点是[ B ]。

A ．aB ．bC ．cD ．d3. 下列说法中正确的是（ D ）A ． 加速度恒定不变时，物体的运动方向也不变；B ．平均速率等于平均速度的大小；C. 当物体的速度为零时，加速度必定为零；D ．质点作曲线运动时，质点速度大小的变化产生切向加速度，速度方向的变化产生法向加速度。

4. 设木块沿光滑斜面从下端开始往上滑动，然后下滑，则表示木块速度与时间关系的 曲线（如图1-99所示）是[ D ]。

二、填空题1. 一质点沿x 轴运动，其运动方程为225t t x -+=（SI ）。

质点的初速度为 2m/s ，第4秒末的速度为 -6m/s ，第4秒末的加速度为-2m/s 2。

2. 质点作直线运动，其速度与时间的关系曲线如图1-100所示。

图中过A 点的一切线AC 的斜率表示 t 1 时刻加速度 ，割线AB 的斜率表示 t 1 时刻到t 2时刻的平均加速度 ，曲线下的面积()⎰21t t dt t v 表示 从t 1时刻到t 2时刻质点的位移 。

三、计算题1. 已知质点的运动方程为t x 2=，24t y -=（SI ）。

试求：（1）试导出质点的轨道方程，并图示质点的运动轨迹；（2）计算t=1s 和t=2s 时质点的位置矢量，并计算1s 到2s 之间质点的平均速度和位移；（3）计算质点在第2秒末时的速度和加速度，并说明质点作何种运动？答：(1)由2x t =得2xt = ，代入22y t =-224x =-即为轨道方程。

高一数学必修1第一章测试题及答案高一第一章测试题（一）一．选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项符合题目要求。

）1.设集合 $A=\{x\in Q|x>-1\}$，则（）A。

$\varnothing \in A$ B。

$2\in A$ C。

$2\in A$ D。

$\{2\}\subseteq A$2.已知集合 $A$ 到 $B$ 的映射 $f:x\rightarrow y=2x+1$，那么集合 $A$ 中元素 $2$ 在 $B$ 中对应的元素是：A。

$2$ B。

$5$ C。

$6$ D。

$8$3.设集合 $A=\{x|1<x<2\},B=\{x|x<a\}$。

若 $A\subseteq B$，则 $a$ 的范围是()A。

$a\geq 2$ B。

$a\leq 1$ C。

$a\geq 1$ D。

$a\leq 2$4.函数 $y=2x-1$ 的定义域是（）A。

$(,\infty)$ B。

$[。

\infty)$ C。

$(-\infty,)$ D。

$(-\infty,]$5.全集 $U=\{0,1,3,5,6,8\}$，集合 $A=\{1,5,8\},B=\{2\}$，则集合 $B$ 为（）A。

$\{0,2,3,6\}$ B。

$\{0,3,6\}$ C。

$\{2,1,5,8\}$ D。

$\varnothing$6.已知集合 $A=\{x-1\leq x<3\},B=\{x^2<x\leq 5\}$，则$A\cap B$ 为（）A。

$(2,3)$ B。

$[-1,5]$ C。

$(-1,5)$ D。

$(-1,5]$7.下列函数是奇函数的是（）A。

$y=x$ B。

$y=2x-3$ C。

$y=x^2$ D。

$y=|x|$8.化简：$(\pi-4)+\pi=$（）A。

$4$ B。

$2\pi-4$ C。

$2\pi-4$ 或 $4$ D。

$4-2\pi$9.设集合 $M=\{-2\leq x\leq 2\},N=\{y\leq y\leq 2\}$，给出下列四个图形，其中能表示以集合 $M$ 为定义域，$N$ 为值域的函数关系的是（）无法呈现图片，无法回答）10.已知$f(x)=g(x)+2$，且$g(x)$ 为奇函数，若$f(2)=3$，则 $f(-2)=$A。

课后习题答案：1、（1）P=3,Q=4; (2)|Ed|=3/2; (3)征税12、(1)X需求曲线为X=500/Px; (2)X=20, Y=50第一部分：需求和供给单选题0、生产可能性曲线上任何一点都隐含着资源配置是（）A.效率最大B.无效率C.有效率，但效率最低D.不一定1、影响需求量的主要因素中不包括( )A.产品价格B.消费者收入C.广告费用D.产品成本2、当需求的收入弹性为负值时，则这种产品应为( )A.低档货B.高档货C.正常货D.都有可能3、某企业生产甲、乙两种产品。

在企业现有资源的条件下，当生产甲产品12000单位时，可生产乙产品9000单位；当甲产品产量提高到14000单位时，乙产品的产量最大可达6000单位。

则乙产品转换为甲产品的边际转换率为( )A.0.15B.6.67C.1.5D.0.6674、影响供给量的主要因素不包括( )A.产品价格B.产品成本C.生产者对价格的预期D.消费者对未来价格的预期5、下列产品中，( )的收入弹性最大。

A.大米B.棉布C.高级工艺品D.食盐6、当某种商品处于( )时，不管价格上升还是下降，其销售收入均保持不变。

A.弹性需求B.单元弹性需求C.非弹性需求D.价格弹性大于17、下面哪种情况将导致供给的减少( )。

A.消费者收入的增加B.采用更加先进的技术C.消费者收入的减少D.生产成本的上升8、下列哪一项会导致粮食制品的均衡价格的下降?（）A.鸡蛋价格的增加B.良好的气候条件C.牛奶价格的下降D.收入的增加10、若需求曲线为一直线，则当价格从高到低不断下降时，卖者的总收益（）A. 不断增加B. 在开始时增加，达到最大值后趋于减少C. 不断减少D. 在开始时趋于减少，达到最小值后趋于增加11、收入和偏好是（）A. 影响供给的因素B. 影响需求的因素C. 在经济分析中可以忽略D. 上述都不准确12、导致需求量沿商品的需求曲线变动的现象发生的情况是（）A. 购买者的收入增加时B. 其它商品价格变化时C. 购买者的偏好变化时D. 当该商品价格下降时13、当社会上各种商品的供求平衡时，价格上涨( )A.能刺激生产，不能抑制需求B.不能刺激生产，能抑制需求C.能刺激生产，能抑制需求D.不能刺激生产，不能抑制需求14、提价1倍后，对需求量不会有很大影响的商品是( )A.彩电B.自行车C.食盐D.高级服装15、在得出某种商品的个人需求曲线时，不保持．．．为常数的因素是（）A. 个人收入B. 其余商品的价格C. 所考虑商品的价格D. 个人偏好16、销售收入与产品价格之间的关系为（）A. 产品价格上涨时，产品销售收入一定增加B. 产品价格上涨时，产品销售收入一定减少C. 产品价格上涨时，产品销售收入可能增加，也可能减少D. 产品价格上涨时，产品销售收入一定保持不变17、不会．．使需求曲线移动的因素是（）A.消费者收入的增加B.商品价格下降C.其他有关商品价格下降D.消费者偏好变化18、需求和供给同时减少的情况下（）A.均衡价格的变化无法确定，均衡交易量将下降B.均衡价格将下降，均衡交易量的变化无法确定C.均衡价格和均衡交易量都将下降D.均衡价格将上升，均衡交易量将下降19、在某一时期内彩色电视机的需求曲线向左平移的原因是（）A.彩色电视机的价格上升B.消费者对彩色电视机的预期价格上升C.消费者对彩色电视机的预期价格下降D.黑白电视机的价格上升20、下列哪种情况会导致需求曲线向左移?( )A. 互补商品价格涨价B.C. 消费者对该商品的偏好上升D.21、如果政府干预市场，并对某种竞争性商品实现最高限价，则会有( )A. 供大于求B. 排队购买该商品C. 厂商增加D.补21、高于均衡价格的现象说明（）A、市场处于一种供大于求的状态；B、市场处于一种供不应求的状态C、市场处于一种既不是供大于求，又不是供不应求的状态D、市场处于一种出清的状态22、某商品的价格从5美元下降到4美元，需求量增加了100单位，需求为（）A．缺乏弹性；B．富有弹性；C．不能确定； D. 单位弹性；23、收入的增加会导致( )。

精品文档集合与函数基础测试一、选择题 ( 共 12 小题，每题 5 分，四个选项中只有一个符合要求)．函数 y＝＝ x2－x＋10在区间（，）上是（）1624A．递减函数B．递增函数C．先递减再递增D．选递增再递减．x y22．方程组{x y 0 A．{( 1,1)}的解构成的集合是（）B．{1,1}C．（1，1）D．{1}3．已知集合 A a，b，c},下列可以作为集合 A 的子集的是（）={A. aB. {a，c}C. {a， e}D.{a， b，c，d}4．下列图形中，表示M N 的是（）M NN M M N MNAB C D5．下列表述正确的是（）A.{ 0}B.{ 0}C.{ 0}D.{ 0}6、设集合 A＝{x|x 参加自由泳的运动员 } ，B＝{x|x 参加蛙泳的运动员 } ，对于“既参加自由泳又参加蛙泳的运动员”用集合运算表示为()A.A∩BB.A BC.A∪BD.A B7. 集合 A={x x2k, k Z } ,B={x x2k1, k Z } ,C={ x x 4k1, k Z } 又a A,b B, 则有（）A. （ a+b） AB. (a+b)BC.(a+b) CD. (a+b)A、B、C任一个）8．函数 f （x）＝－ x2＋（ a－） x＋2在（－∞，）上是增函数，则 a 的范围是（214A． a≥5B．a≥3C．a≤3D．a≤－ 59. 满足条件 {1,2,3}M{1,2,3,4,5,6}的集合 M的个数是（）A. 8B. 7C. 6D.510.全集 U={1，2 ，3，4 ，5 ，6 ，7，8}，A={3 ，4，5} ，B={1 ，3 ，6} ，那么集合 { 2，7 ，8}是（）A.ABB. A BC.C U A C U BD.C U A C U B11. 下列函数中为偶函数的是（）A．y x B． y x C． y x2D． y x31 12. 如果集合 A={ x | ax 2＋ 2x ＋ 1=0}中只有一个元素，则 a 的值是（）A．0B．0 或1C．1D．不能确定二、填空题 ( 共 4 小题，每题 4分，把答案填在题中横线上 )．函数 f （x）＝× －｜ x｜的单调减区间是．13223___________．函数 y＝ 1 的单调区间为___________．14x＋115. 含有三个实数的集合既可表示成{ a,b,1}，又可表示成{ a2, a b,0}，则a2 0 0 3 b2 0 0 4a .。

集合练习题一．选择题1．满足条件{1,2,3}⊂≠M ⊂≠{1,2,3,4,5,6}的集合M 的个数是（ ）A 、8 B 、7 C 、6 D 、52．若集合{}0|2≤=x x A ，则下列结论中正确的是（ ）A 、A=0B 、0A ⊆C 、∅=AD 、A ∅⊆ 3．下列五个写法中①{}{}2,1,00∈，②{}0≠⊂∅，③{}{}0,2,12,1,0⊆，④∅∈0，⑤∅=∅ 0，错误的写法个数是（ ）A 、1个 B 、2个 C 、3个 D 、4个4．方程组⎩⎨⎧-=-=+11y x y x 的解集是 （ ）A 、{}0,1x y ==B 、{}1,0C 、{})1,0(D 、{}(,)|01x y x y ==或 5．设A 、B 是全集U 的两个子集，且A ⊆B ，则下列式子成立的是（ ）A 、C U A ⊆C UB B 、C U A ⋃C U B=U C 、A ⋂C U B=φD 、C U A ⋂B=φ 6．已知全集⎭⎬⎫⎩⎨⎧∈∈-=Z a N a a M 且56|,则M=( ) A 、{2，3} B 、{1，2，3，4} C 、{1，2，3，6} D 、{-1，2，3，4}7．集合},02{2R x a x x x M ∈=-+=，且φM ，则实数a 的X 围是（）A 、1-≤aB 、1≤aC 、1-≥aD 、1≥a8. 设集合P 、S 满足P ⋂S=P ，则必有（ ）A 、P S ；B 、P ⊆S ；C 、S P ；D 、S=P 。

9. 设全集},,,,{e d c b a U =，A 、B 都是U 的子集}{e B A =⋂，}{d B A C U =⋂，},{b a B C A C U U =⋂，则下列判断中正确的是（ ）A 、c A 且cB ； B 、c A 且cB ；C 、c A 且cB ； D 、c A 且c B 。

10. 若C A B A ⋃=⋃，则一定有（ ）A 、B=C ；B 、C A B A ⋂=⋂； C 、C C A B C A U U ⋃=⋂；D 、C A C B A C U U ⋂=⋂ 。

一.选择题:［B］1、[基础训练2]一质点沿x轴作直线运动，其v-t曲线如图所示，如t=0时，质点位于坐标原点，则t=4.5 s时，质点在x轴上的位置为(A) 5m．(B) 2m．(C) 0．(D) -2 m．(E) -5 m.【答】4.5sx vdt=⎰，质点在x轴上的位置即为这段时间内v-t曲线下的面积的代数和：(1 2.5)22(21)122()x m=+⨯÷-+⨯÷=［A］2、[基础训练5] 一条河在某一段直线岸边同侧有A、B两个码头，相距1 km。

甲、乙两人需要从码头A到码头B，再立即由B返回。

甲划船前去，船相对河水的速度为4 km/h；而乙沿岸步行，步行速度也为4 km/h．如河水流速为2 km/h, 方向从A到B，则(A) 甲比乙晚10分钟回到A．(B) 甲和乙同时回到A．(C) 甲比乙早10分钟回到A．(D) 甲比乙早2分钟回到A．【答】甲：()()112()42423A B B At t t h→→=+=+=+-甲；乙：1122 ()42A B B A A Bt t t t h→→→=+==⨯=乙；∴1()10 (min)6t t t h∆=-==甲乙［C］3、[自测提高1]如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动．设该人以匀速率v收绳，绳不伸长、湖水静止，则小船的运动是(A) 匀加速运动．(B) 匀减速运动．(C) 变加速运动．(D) 变减速运动．(E) 匀速直线运动．【答】如图建坐标系，设船离岸边x米，222l h x=+，22dl dxl xdt dt=，dx l dl dldt x dt x dt==，dlvdt=-，22dx h xv i v idt x+==--12223v hdv dv dxa idt dx dt x==⋅=-，可见，加速度与速度同向，且加速度随时间变化。

［B］4、（自测提高3）质点沿半径为R的圆周作匀速率运动，每T秒转一圈．在2T 时间间隔中，其平均速度大小与平均速率大小分别为(A) 2πR/T , 2πR/T．(B) 0 , 2πR/T(C) 0 , 0．(D) 2πR/T , 0.【答】平均速度大小：0rvt∆==∆平均速率：2s Rvt T∆==∆π［C］5、[自测提高6]某物体的运动规律为tkt2d/d vv-=，式中的k为大于零的常量．当0=t时，初速为v，则速度v与时间t的函数关系是(A)221vv+=kt, (B)221vv+-=kt,(C)2121vv+=kt, (D)2121vv+-=kt【答】tkt2d/d vv-=，分离变量并积分，2v tvdvktdtv=-⎰⎰，得2121vv+=kt.［B］6、[自测提高7]在相对地面静止的坐标系内，A、B二船都以2 m/s速率匀速行驶，A船沿x轴正向，B船沿y轴正向．今在A船上设置与静止坐标系方向相同的坐标系(x、y 方向单位矢用i、j表示)，那么在A船上的坐标系中，B船的速度（以m/s为单位）为(A) 2i＋2j．(B) -2i＋2j．(C) －2i－2j．(D) 2i－2j．【答】B A对v=B对v地+A对v地=B对v地-A对v地=2222 (/)j i i j m s-=-+.二.填空题7、[基础训练10] 一物体作如图所示的斜抛运动，测得在轨道A点处速度v的大小为v，其方向与水平方向夹角成30°，则物体在A点的切向加速度a t = -0.5g ，轨道的曲率半径2vg.（重力加速度为g）【答】如图，将重力加速度分解为切向加速度分量和法向加速度分量，得2200sin300.5,cos30cos30t nv va g g a ggρρ=-=-==∴=8、[基础训练12] 一质点沿直线运动,其运动学方程为x = 6 t－t2(SI)，则在t由0至4s的时间间隔内，质点的位移大小为 8 ()m，在t由0到4s的时间间隔内质点走过的路程为 10 ()m．【答】（1）x = 6 t－t2(SI)，位移大小()24064408 ()r x x m∆=-=⨯--=；（2）62x dxv t dt==-，可见，t<3s 时，x v >0；t=3s 时，x v =0；而t>3s 时，x v <0；所以，路程=()()()3034()909810 ()x x x x m -+-=-+-=9、[基础训练13]在xy 平面内有一运动质点，其运动学方程为：jt i t r5sin 105cos 10+=（SI ），则t 时刻其速度=v(m/s) )5cos 5sin (50 j t i t+-；其切向加速度的大小a t = 0 ；该质点运动的轨迹是 圆 ． 【答】（1）50(sin5cos5) (m/s)drv t i t j dt==-+； （2）速率50 /v m s =，切向加速度0t dva dt== （3）10cos5x t =，t y 5sin 10=，可见，22100x y +=，轨迹为一个圆。

概率论11、甲、乙两艘轮船驶向一个不能同时停泊两艘船的码头停泊.它们在一昼夜内到达码头的时刻是等可能的.如果甲船停泊的时间是一小时,乙船停泊的时间是两小时,求这两艘船都不等候码头的概率. 解：分别用x、y表示甲、乙船到达时刻，在直角坐标系下作直线x=24、y=24，它们与x轴及y轴围成一个正方形，点(x,y)总是落入这个正方形的；作直线y=x+1与y=x-2，如果点(x,y)落入两直线所夹以外区域就不需要等待，所以不需要等待的概率为：p=(22*22/2+23*23/2)/(24*24)=1013/1152≈0.87934027777777825、已知男人中5%是色盲患者，女人中有0.25%；今从男女人数相等的人群中随机挑选一人，恰好是色盲患者，问此人是男人的概率是多少？解：可以算出色盲的人占总人数的比率是5%x50%+0.25%x50%=2.625%，而在2.625%的人中，男的占5%x50%，所以是男的几率为5%x50%除以2.625%=20/21第一章随机事件与概率1．设A，B，C为三个事件，试用A、B、C表示下列事件，并指出其中哪俩个事件是互逆事件：1）仅有一个事件发生；2）至少有一个事件发生；3）三个事件都发生；４）至多有两个事件发生；５）三个事件都不发生；６）恰好两个事件发生。

用a,b,c分别表示A,B,C的补事件,那么有1)abC∪aBc∪Abc2)1-abc3)ABC4)1-ABC5)abc6)ABc∪AbC∪aBC其中(2)和(5) (3)和(4) 是互逆事件2．设对于事件A，B，C，有P（A）=P（B）=P（C）=1/4，P（AC）=1/8，P（AB）=P（BC）=0，求A、B、C至少出现一个的概率。

因为P（AB）=0，所以P（ABC）=0，所以P（A+B+C）=PA+PB+PC-PAB-PAC-PBC+PABC=5/83．设A，B为随机事件，P（A）=0.7，P（A-B）=0.3，求P（AB(—)）。

1.1同底数幂的乘法一、单选题1.计算3()()x y x y -⋅-=（ ）.A.4()x y -B.3()x y -C.4()x y --D.4()x y +2.下列计算过程正确的是( )A.2358x x x x ⋅⋅=B.347x y xy ⋅=C.57(9)(3)3-⋅-=-D.56()()x x x --= 3.下列各式的计算结果为7a 的是( )A.25()()a a -⋅-B.25()()a a -⋅- C.25()()a a -⋅- D.6()()a a -⋅- 4.当0,a n <为正整数时，52()()n a a -⋅-的值 ( )A.正数B.负数c.非正数 D.非负数 5.10,10x ya b ==,则210x y ++等于( )A.2abB.a b +C.2a b ++D.100ab6.已知2,3,m n x x ==则m n x +的值是( )A.5B. 6C. 8D. 97.计算·53a a 正确的是( ) A. 2aB. 8aC. 10aD.15a8.在等式3211()a a a ⋅⋅=中,括号里面的代数式是( ).A.7aB.8aC.6aD.3a9.已知m n 34a a ==，,则m+n a 的值为（ ）.A.12B.7 二、解答题10.求下列各式中x 的值.(1)21381243;x +=⨯(2)3141664 4.x -⨯=⨯三、填空题11.已知34x =，则23x += .12.计算34x x x ⋅+的结果等于________.13.已知1428m +=，则4m = .14.若2m 5x x x ⋅=，则m =_____.参考答案1.答案：A解析：2.答案：D解析：选项A 中，2351359x x x x x ++⋅⋅==，故本选项错误;选项B 中，3x 与4y 不是同底数幕，不能运算，故本选项错误;选项C 中，5257(9)(3)3(3)3-⋅-=-⋅-=，故本选项错误;选项D 中，5516()()()x x x x +--=-=，故本选项正确.故选D3.答案：C解析：选项A 中，275()()a a a -⋅-=-，故此选项错误;选项B 中,257()()a a a -⋅-=-，故此选项错误;选项C 中，275()()a a a -⋅-=，故此选项正确;选项D 中，67()()a a a ⋅-=--.故此选项错误.4.答案：A解析：5225()()(),n n a a a +-⋅-=-∴当0,a n <为正整数，即0a ->时,25()0,n a +->是正数5.答案：D解析：2210101010100x y x y ab ++=⨯⨯=.6.答案：B解析：2,3,23 6.m n m n m n x x x x x +==∴=⋅=⨯=7.答案：B解析：8.答案：C解析：9.答案：A解析：10.答案：解(1)21381243x +=⨯2145333x +=⨯则219x +=解得4x =（2）31416644x -⨯=⨯3124444x -⨯=314x +=则1x =解得解析：11.答案：36解析：223334936x x +=⋅=⨯=.12.答案：42x解析：13.答案：7解析：因为11444m m +=⨯，所以4428m ⨯=,所以47.m =14. 答案：3 1.2幂的乘方与积的乘法一、单选题1.下列运算正确的是( )A.326x x x ⋅=11=C.224+=x x xD.()22436x x = 2.计算(-2x 2)3的结果是( )A.-8x 6B.-6x 6C.-8x 5D.-6x 53.下列各式计算正确的是( )A. 235ab ab ab +=B. ()22345a ba b -=C. =D. ()2211a a +=+4.计算(-xy 2)3的结果是( )A.-x 3y 6B.x 3y 6C.x 4y 5D.-x 4y 55.下列运算正确的是( )A.x 2·x 3=x 6B.x 3+x 2=x 5C.(3x 3)2=9x 5D.(2x)2=4x 26.计算正确的是( )A.a 3-a 2=aB.(ab 3)2=a 2b 5C.(-2)0=0D.3a 2·a -1=3a 7.下列计算正确的是( )A.a 3·a 2=a 6B.3a+2a 2=5a 2C.(3a)3=9a 3D.(-a 3)2=a 6 8.计算(-x 2)3的结果是( )A.-x 5B.x 5C.x 6D.-x 6 9.计算(-a 2)5的结果是( )A.a 7B.-a 7C.a 10D.-a 10 二、解答题10.已知 333,2,m n a b ==求()()332242m n m n m n a b a b a b ⋅+-的值 。

物理光学习题 第一章 波动光学通论一、填空题（每空2分）1、．一光波在介电常数为ε，磁导率为μ的介质中传播，则光波的速度v= 。

【εμ1=v 】2、一束自然光以 入射到介质的分界面上，反射光只有S 波方向有振动。

【布儒斯特角】3、一个平面电磁波波振动表示为 E x =E z =0, E y =cos[⎪⎭⎫⎝⎛-⨯t c x 13102π], 则电磁波的传播方向 。

电矢量的振动方向 【x 轴方向 y 轴方向】4、在光的电磁理论中，S 波和P 波的偏振态为 ，S 波的振动方向为 ， 【线偏振光波 S 波的振动方向垂直于入射面】5、一束光强为I 0的自然光垂直穿过两个偏振片，两个偏振片的透振方向夹角为45°，则通过两偏振片后的光强为 。

【I 0/4】6、真空中波长为λ0、光速为c 的光波，进入折射率为n 的介质时，光波的时间频率和波长分别为 和 。

【c/λ0 λ0 /n 】7、证明光驻波的存在的维纳实验同时还证明了在感光作用中起主要作用是 。

【电场E 】8、频率相同，振动方向互相垂直两列光波叠加，相位差满足 条件时，合成波为线偏振光波。

【0 或Π】9、会聚球面波的函数表达式 。

【ikre rA r E -)(=】 10、一束光波正入射到折射率为1.5的玻璃的表面，则S 波的反射系数为 ，P 波透射系数： 。

【-0.2 0.2 】11、一束自然光垂直入射到两透光轴夹角为θ的偏振片P 1和P 2上，P 1在前，P 2在后，旋转P 2一周，出现 次消光，且消光位置的θ为 。

【2 Π/2】12、当光波从光疏介质入射到光密介质时，正入射的反射光波 半波损失。

（填有或者无） 【有】13、对于部分偏振光分析时，偏振度计算公式为 。

（利用正交模型表示） 【xy x y I I I I P +-=】二、选择题（每题2分）1．当光波从光密介质入射到光疏介质时，入射角为θ1，布儒斯特角为θB ，临界角为θC ，下列正确的是 （ ）A ．0<θ1<θB , S 分量的反射系数r S 有π位相突变 B ．0<θ1<θB , P 分量的反射系数r P 有π位相突变C ．θB <θ1<θC , S 分量的反射系数r S 有π位相突变D ．θB <θ1<θC , P 分量的反射系数r P 有π位相突变 【B 】2．下面哪种情况产生驻波 （ ） A ．两个频率相同，振动方向相同，传播方向相同的单色光波叠加 B ．两个频率相同，振动方向互相垂直，传播方向相反的单色光波叠加 C ．两个频率相同，振动方向相同，传播方向相反的单色光波叠加 D ．两个频率相同，振动方向互相垂直，传播方向相同的单色光波叠加 【C 】3．平面电磁波的传播方向为k ，电矢量为E ，磁矢量为B, 三者之间的关系下列描述正确的是 （ ） A ．k 垂直于E ， k 平行于B B ．E 垂直于B ， E 平行于k C ．k 垂直于E ， B 垂直于k D ．以上描述都不对 【C 】4、由两个正交分量]cos[0wt kz A x E x -= 和]87cos[0π+-=wt kz A y E y表示的光波，其偏振态是（ ）A 线偏振光B 右旋圆偏振光C 左旋圆偏振光D 右旋椭圆偏振光 【D 】5、一列光波的复振幅表示为ikre rA r E =)(形式，这是一列（ ）波 A 发散球面波 B 会聚球面波 C 平面波 D 柱面波 【A 】6、两列频率相同、振动方向相同、传播方向相同的光波叠加会出现现象（ ） A 驻波现象 B 光学拍现象 C 干涉现象 D 偏振现象 【C 】7、光波的能流密度S 正比于（ ）A E 或HB E 2或H 2C E 2，和H 无关D H 2，和E 无关 【B 】8、频率相同，振动方向互相垂直两列光波叠加，相位差满足（ ）条件时，合成波为二、四象限线偏振光波。

成人高考《高等数学一》章节练习题答案及解析- 1 -2021 年专升本数学一习题第一章极限、连续1.已知f(x) = � 3x + 2，x ≥0x 2 −1,x < 0。

求f（0）=2. limx→∞sinxx=3. limx→2 （x −2）sin1x−2=4. limx→0xln(3x+1)=5. limx→0sin4xx=6. limx→∞�1 +5x �x =7. limx→0tan2x2x=8. limx→0 (1 −x)1x =9. limx→0 (1 + x)−1x =10. limx→∞�1 +1x �x+2 =11. limx→0x ⋅tanx= 12. limx→0sinxsin2x =13. limx→0ln (2x+1)sin3x14. limx→1x−1x 2 −1=15. limx→4x−4√x+5−3=- 2 -- 2 -16. limx→∞2x 3 +3x 2 +5 7x 3 +4x 2 −1 = 17.设f(x) = �x −1,x < 0 0,x = 0x + 1,x > 0，求limx→0f(x)18. limx→2x 2 +x−6x 2 −4=19. limx→0x−sinxx 2 +x=20.设函数f(x) = �√x3,x < 0,x 2 + 1,x ≥0, 则在点x=0 处是否连续。

21.函数f(x) =x 2 +1x−3的间断点是（）。

22.设函数f(x) = �e x，x < 0x + a，x ≥0 在x=0 处连续，则a=（）第二章一元函数微分学1.已知f ′(2) = 2，求limΔx→0f(2−3Δx)−f(2)Δx=2.已知f ′(4) = 1，求limΔx→0f(4+2Δx)−f(4)Δx=3x + lnx在点（1，0）处切线斜率K。

4lnx在点（1,0）处的切线方程和法线方程。

5x 2 上的一点，使该点处的切线与直线y = 2x + 2平行。

七年级数学上册《第一章有理数的乘方》同步练习题含答案(冀教版）学校:___________班级：___________姓名：___________考号：___________一、选择题1.比较(﹣4)3和﹣43，下列说法正确的是( )A.它们底数相同，指数也相同B.它们底数相同，但指数不相同C.它们所表示的意义相同，但运算结果不相同D.虽然它们底数不同，但运算结果相同2.下列几组数中，互为相反数的是( )A.﹣(＋5)和＋(﹣5)B.(﹣3)2和(＋3)2C.﹣(﹣4)和﹣|﹣4|D.(﹣2)3和﹣233.在|﹣2|，﹣|0|，(﹣2)5，﹣|﹣2|，＋(﹣2)中，负数共有( )A.1 个B.2个C.3个D.4个4.下列说法正确的是( )A.23表示2×3的积B.任何有理数的偶次方都是正数C.一个数的平方是9，这个数一定是3D.-32与(-3)2互为相反数5.下列各组数中，数值相等的是( ).A.23和32B.﹣22和(﹣2)2C.﹣33和(﹣3)3D.(﹣3×2)2和﹣32×226.下列说法，正确的有( ).(1)整数和分数统称为有理数；(2)任何有理数都有倒数；(3)一个数的绝对值一定为正数；(4)立方等于本身的数是1和﹣1.A.1个B.2个C.3个D.4个7.下列结论正确的是( )A.两个负数，绝对值大的反而小B.两数之差为负，则这两数异号C.任何数与零相加，都得零D.正数的任何次幂都是正数；负数的偶次幂是负数8.计算：31＋1＝4，32＋1＝10，33＋1＝28，34＋1＝82，35＋1＝244，…，归纳计算结果中的个位数字的规律，猜测32009＋1的个位数字是( )A.0B.2C.4D.8二、填空题9.计算：(﹣2)3= .10.计算：(1)(－5)2=_______；(2)－52=_______；(3)(－27)3=_____；(4)－237=______. 11.若a ，b 互为倒数，则a 2b ﹣(a ﹣2027)值为 .12.若|x ﹣3|＋(y ＋2)2＝0，则x 2y 的值为 .13.平方等于16的数有 ，立方等于﹣1的数是 .14.若(m ﹣2)2＋|n ＋3|＝0，则n m 的值是 .三、解答题15.计算：﹣14﹣2×(﹣3)216.计算：8﹣23÷(﹣4)×(﹣3＋1).17.计算：-12-23÷（-4）×（-7+5）.18.计算：-（-3-5）+（-2）2×5+（-2）319.(1)在数轴上把下列各数表示出来：﹣1，﹣|﹣2.5|，﹣(﹣2)，(﹣1)100，﹣22(2)将上列各数用“＜”连接起来： .20.已知(x﹣2)2＋|y＋3|＝0，求y x﹣xy的值.21.规定“*”是一种运算，且a*b＝a b﹣b a，例如：2*3＝23﹣32＝8﹣9＝﹣1，试计算4*(3*2)的值.22.阅读下列材料，并回答问题计算机利用的是二进制数，它共有两个数码：0，1；将一个十进制的数转化为二进制数，只需把该数写成若干个的数的和，依次写出1或0即可．例如十进制数19可以按下述方法转化为二进制数：19＝16＋2＋1＝1×24＋0×23＋0×22＋1×21＋1×20＝10011．二进制数110110可以转换成十进制数为：110110＝1×25＋1×24＋0×23＋1×22＋1×21＋0×20＝54．(1)将86化成二进制；(2)将1011101化成十进制．参考答案1.D.2.C3.C.4.D5.C.6.C7.A8.C9.答案为：﹣8.10.答案为：(1)25 (2)－25 (3)－8343(4)－8711.答案为：2027.12.答案为：﹣18.13.答案为：4、﹣4，﹣1.14.答案为：9.15.解：原式＝﹣1﹣18＝﹣19.16.解：8﹣23÷(﹣4)×(﹣3＋1)＝8﹣8÷(﹣4)×(﹣2)＝8＋2×(﹣2)＝8﹣4＝417.解：原式=－5.18.解：原式=1419.解：如图所示；(2)由图可知，﹣22＜﹣|﹣2.5|＜﹣1＜(﹣1)100＜﹣(﹣2).20.解：∵(x﹣2)2＋|y＋3|＝0∴x﹣2＝0，x＝2；y＋3＝0，y＝﹣3；则y x﹣xy＝(﹣3)2﹣2×(﹣3)＝9＋6＝15.故答案为15.21.解：根据题中的新定义得：原式＝4*(9﹣8)＝4*1＝4﹣1＝3.22.解：(1)86÷2＝4343÷2＝21 (1)21÷2＝10 (1)10÷2＝5 05÷2＝2 (1)2÷2＝1 01÷2＝0 (1)故86(10)＝1010110(2)．(2)(1011101)2＝1×26＋0×25＋1×24＋1×23＋1×22＋0×21＋1×20＝64＋0＋16＋8＋4＋0＋1＝93；(1011101)2＝(93)10．。

1.l 解释下列名词摩尔定律：对集成电路上可容纳的晶体管数目、性能和价格等发展趋势的预测，其主要内容是：成集电路上可容纳的晶体管数量每18个月翻一番，性能将提高一倍，而其价格将降低一半。

主存: 计算机中存放正在运行的程序和数据的存储器，为计算机的主要工作存储器，可随机存取。

控制器：计算机的指挥中心，它使计算机各部件自动协调地工作。

时钟周期：时钟周期是时钟频率的倒数，也称为节拍周期或T周期，是处理操作最基本的时间单位。

多核处理器：多核处理器是指在一枚处理器中集成两个或多个完整的计算引擎(内核)。

字长：运算器一次运算处理的二进制位数。

存储容量: 存储器中可存二进制信息的总量。

CPI：指执行每条指令所需要的平均时钟周期数。

MIPS：用每秒钟执行完成的指令数量作为衡量计算机性能的一个指标，该指标以每秒钟完成的百万指令数作为单位。

CPU时间：计算某个任务时CPU实际消耗的时间，也即CPU真正花费在某程序上的时间。

计算机系统的层次结构：计算机系统的层次结构由多级构成，一般分成5级，由低到高分别是：微程序设计级，机器语言级，操作系统级，汇编语言级，高级语言级。

基准测试程序：把应用程序中使用频度最高的那那些核心程序作为评价计算机性能的标准程序。

软/硬件功能的等价性：从逻辑功能的角度来看，硬件和软件在完成某项功能上是相同的，称为软/硬件功能是等价的，如浮点运算既可以由软件实现，也可以由专门的硬件实现。

固件：是一种软件的固化，其目的是为了加快软件的执行速度。

可靠性：可靠性是指系统或产品在规定的条件和规定的时间内，完成规定功能的能力。

产品可靠性定义的要素是三个“规定”：“规定条件”、“规定时间”和“规定功能”。

MTTF：平均无故障时间，指系统自使用以来到第一次出故障的时间间隔的期望值。

MTTR：系统的平均修复时间。

MTBF：平均故障间隔时间，指相邻两次故障之间的平均工作时间。

可用性：指系统在任意时刻可使用的概率，可根据MTTF、MTTR和MTBF等指标计算处系统的可用性。