一笔画图

【精品】如果用笔在纸上连续不断，又不重复，一笔画成某种图形，那么这种图形就叫做一笔画.没有连成一体的图形叫做不连通图，如“吕”、“品”字图等；连成一体的图形叫做连通图，如“串”字图等.任何图形都是由点和线组成的.图形中的点可以分成两类：凡是从一个点出发的线的数目是偶数的，这个点称为偶点.凡是从一个点出发的线的数目是奇数的，这个点称为奇点.一笔画的基本规律：能一笔画出的图形必须是连通的；凡是只由偶点组成的连通图形，一定可以一笔画，画时可以由任一偶点为起点，最后仍回到这点；凡是只有两个奇点的连通图形，一定可以一笔画，画时必须以一个奇点为起点，以另一个奇点为终点；奇点的个数一定为偶数，奇点个数超过两个的图形不能一笔画，所需的最少笔数等于奇数点的个数除以2.判断下列图形能否一笔画，如果能，试着将它们画出来.解析：能够一笔画的字有：口，中，日；能够一笔画的图形有，。

标出下列各个图形各结点的奇偶性，并判断它们能否一笔画.解：各结点奇偶性如下图所示：1 422234441133332222444433211222能够一笔画的有图1、2、4.标出下列各个图形各结点的奇偶性，并判断它们能否一笔画.解：能够一笔画的有图3、4.在六面体的顶点B和E处各有一只蚂蚁(见下图)，它们比赛看谁能爬过所有的棱线，最终到达终点D.已知它们的爬速相同，哪只蚂蚁能获胜？解析：大多同学可能看不出这是一笔画问题，但利用一笔画的知识，能非常巧妙地解答这道题.这道题只要求爬过所有的棱，没要求不能重复.可是两只蚂蚁爬速相同，如果一只不重复地爬遍所有的棱，而另一只必须重复爬某些棱，那么前一只蚂蚁爬的路程短，自然先到达D点，因而获胜.问题变为从B到D与从E到D哪个是一笔画问题.图中只有E，D两个奇点，所以从E到D可以一笔画出，而从B到D 却不能，因此从E点爬的蚂蚁获胜.下图是一个公园的平面图，要使游客走遍公园每条路而不重复，问出入口应设在哪里？HGFED CBA解析：本题实际上是问这个图以哪点为起点与终点的问题，观察上图可以发现，图中只有两个“奇点”B与E，因此出入口应设在B点与E点，即这两点其中一个设为入口，则另一个设为出口.下列各图至少要用几笔才能画成？解析：对于任意连通图来说，如果有n2个奇点（n为自然数），那么这个图一定可以用n笔画成。

一笔画完园的三个扇形摘要：I.引言- 介绍一笔画的概念和挑战- 说明本文的目标：完成一笔画完园的三个扇形II.一笔画的基本原理- 定义一笔画：只用一笔完成图案的绘制- 关键点：每条线段必须与其它线段相交一次且仅一次III.园的三个扇形的绘制方法- 步骤1：绘制第一个扇形1.从园的边缘开始，画一条弧线2.以弧线的终点为圆心，画一个较小的扇形- 步骤2：绘制第二个扇形1.从第一个扇形的终点开始，画一条弧线2.以弧线的终点为圆心，画一个较小的扇形- 步骤3：绘制第三个扇形1.从第二个扇形的终点开始，画一条弧线2.以弧线的终点为圆心，画一个较小的扇形IV.完成一笔画完园的三个扇形- 总结绘制三个扇形的过程- 强调完成一笔画的关键：合理选择起点和路径正文：一笔画是近年来风靡一时的益智游戏，它要求玩家用一笔完成图案的绘制，具有很高的挑战性和趣味性。

本文旨在详细介绍如何完成一笔画完园的三个扇形。

首先，我们需要了解一笔画的基本原理。

一笔画，顾名思义，就是只用一笔完成图案的绘制。

听起来很容易，实则不然。

在绘制过程中，每条线段必须与其它线段相交一次且仅一次，否则就无法完成一笔画。

接下来，我们将详细介绍如何绘制园的三个扇形。

首先，从园的边缘开始，画一条弧线。

然后，以弧线的终点为圆心，画一个较小的扇形。

这是第一个扇形的绘制方法。

接着，从第一个扇形的终点开始，画一条弧线。

同样地，以弧线的终点为圆心，画一个较小的扇形。

这样就完成了第二个扇形的绘制。

最后，从第二个扇形的终点开始，画一条弧线，以弧线的终点为圆心，画一个较小的扇形。

这样，我们就完成了园的三个扇形的绘制。

在绘制过程中，要注意合理选择起点和路径，以确保每条线段都与其它线段相交一次且仅一次。

这样，你就可以顺利地完成一笔画完园的三个扇形。

一笔画【知识要点】1．概念：一笔画是指笔不离开纸，而且每条线都只画一次不准重复而画成的图形。

2．分类：图中的点可分两大类：（1）双数点：从这点出发的线的数目是双数的，叫双数点。

（2）单数点：从这点出发的线的数目是单数的，叫单数点。

3．规律：一个图形能否一笔画成，关键在于图中单数点的多少。

（1）凡是图形中没有单数点的一定可以一笔画成。

（2）凡是图形中只有两个单数点，一定可以一笔画成，画时必须从一个单数点为起点，最后以另一单数点为终点。

（3）凡是图形中单数点的个数多于两个时，此图肯定是不能一笔画成。

【题目】1 判断下面图形中哪些点是单数点哪些点是双数点。

2 下列图形中各有几个单数点？能一笔画成吗？3 判断下面图形能不能一笔画成？如果能，应该怎样画？ADBEABACAB A DE F ACBBCA5 如图是一个大型花池中小路的平面图，你能否不重复地一次走完所有的小路？进出口应设在什么地方？6 将下图加上最少的线改成一笔画的图形。

7．将下图去掉最少的线改成一笔画图形。

8．下图中的线段代表小路，请小朋友想一想，能够不重复地爬遍小路的甲蚂蚁还是乙蚂蚁？该怎么爬？9．为迎接2008年奥运会在北京召开，你能一笔画出奥运会的五环图案吗？10．下图是一个公园的平面图，应怎样走才能使游客走通每条路而不重复，设计一条最佳路线。

A B H C G F E D11 一个公园的平面图如下，请你设计好入口、出口，并给出一条浏览路线，要求走遍每一条路且不重复。

12．如图，是一个公园的平面图，请你设计好入口、出口，并给出一种游玩路线，要求走遍每一条路且不重复。

13．如图，是一个名画展厅的平面图，要使参观者不重复地走遍每一条画廊，问：出口、入口应设在哪里？14．黑色的鱼与白色的鱼所能游动的河道如下图所示。

黑色的鱼在A 点位置，白色的鱼在B点位置。

哪条鱼能不重复地游遍所有的河道？15．能用一根铁丝弯成下面的图形吗？16．一个邮递员投递信件要走的街道如图，为节约时间，他想自己设计一条线路，可以不重复的走遍每一条街道，你能帮帮他吗？17．一只蚂蚁要想不重复的爬遍每一条线路，应从哪里出发，到哪里结束？18．你能用一笔画成4条线段把下图的9个点都连起来吗？A B A BA B CFEA BC EF H IAB19．下图能否一笔画成？如果能，应怎样画？20．如图，在一个六面体的顶点A 和B 处各有一只蜗牛，它们比赛看谁能不重复地爬遍每一棱线到达C点。

一笔画知识点：1.一笔画概念：（用自己的话：一笔画出图）“”由画圆引入“一笔画”的特点：①一笔画成②笔不离纸③不重复（已画成不需重复）。

下面这三个图，同学们先尝试画一下，请3位同学上来画（要求尽量一笔画出）。

①②③大家发现这两个图都可以一笔画出来，可是这些图都比较简单，如果是复杂的图怎么画呢？也是一一尝试吗？所以今天我们学习怎么快速方便的判断图形能否一笔画。

接下来一起观察，大家有没有发现每一个图都是由点和线组成的。

那么我们想要找办法一笔画图肯定跟图中的点和线有关系的。

首先呢，老师要告诉你们这些点都是有名字的，而且呢，这个名字还是由线来命名的哦。

大家是不是很好奇呢？老师把这个点叫做双数点，这边这个叫做单数点，你们知道为什么吗？每个小朋友都有自己的想法，你们听听老师是怎么命名的。

从该点出发，有2条线画出，其实呢，就是从该点出发，发出双数条线的点叫做双数点。

那么谁可以告诉老师，为什么这个点是单数点吗？对了，因为这个图里从这个点出发，发出了3条线。

单数点的概念就是：从该点出发，发出单数条线的点叫做单数点。

到底一笔画跟双数点和单数点有什么关系呢？回过头来我们看看刚刚的图。

首先请同学们迅速的把图中的点找出来，请你在每一个点旁边写上发出线的条数。

仔细观察，谁能告诉老师这些点都是什么点？大家学的都非常快，这些点都是双数点，因为从点出发发出的线都是双数条。

这些图没有单数点，但是大家尝试过，虽然尝试的画法不一样，但是大家都一笔画出来了。

原来没有单数点的图一定可以一笔画。

而且，画时，任意一个双数点既是起点，又是终点。

刚刚讨论的3个图都没有单数点，下面我们看看有单数点的图：④这个图能不能一笔画出呢？同样的，先请同学们找出图上的点，在每一个点旁边写上线的条数。

都写好了吗？那么请个小助手上来告诉老师，哪些点是单数点，用红笔把它圈出来。

这个图上一共有几个单数点？刚刚大家尝试了，这个图可以一笔画的。

那么总结一下：只有两个单数点的图，也可以一笔画。

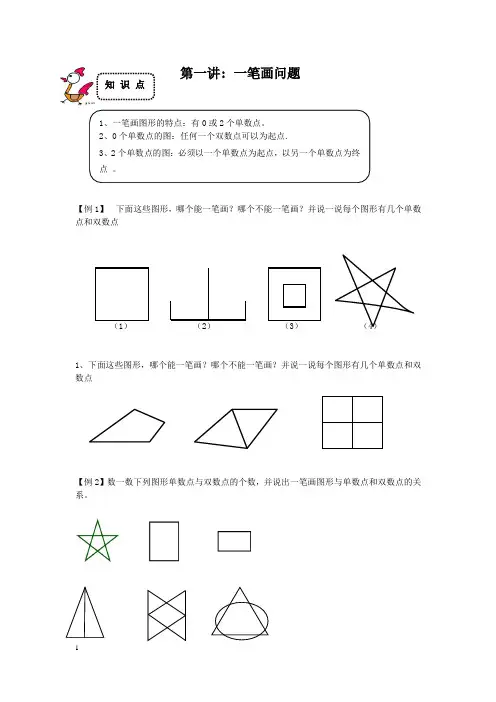
第一讲: 一笔画问题【例1】下面这些图形，哪个能一笔画？哪个不能一笔画？并说一说每个图形有几个单数点和双数点（2）1、下面这些图形，哪个能一笔画？哪个不能一笔画？并说一说每个图形有几个单数点和双数点【例2】数一数下列图形单数点与双数点的个数，并说出一笔画图形与单数点和双数点的关系。

1、下面的图形能否一笔画完成？为什么？（1） O （2）B D（3）【例2】下面的图形能不能一笔画？如果能怎么画？1、下面的图形能不能一笔画？如果能怎么画？【例3】下面的图形能不能一笔画？如果能怎么画？12、34、、、【例4】下图（图1）能否一笔画成，若不能，你能用什么方法把它改成能够一笔画成的图形？1、将下列各图改成一笔画。

【例5】邮递员叔叔要向一个居民小区送信，怎么样走才能少走重复路，使每天走的路尽可能短？1.下图是一个小区中花园的平面图，你能一次不重复地走完所有的路吗？入口和出口应该设计在哪儿呢？2.下面是“儿童乐园”平面图，出口应没在哪里才能不重复地走遍每条路？1.数一数下面图形有几个单数点？2.下列图形能一笔画成吗？为什么？3.甲、乙两辆车同时以相同的速度分别从A 、B 出发，哪辆车能最先行驶完所有的路线？4.园林工人在花园浇花，怎样才能不重复地走遍每一条小路？第 二 讲:巧填竖式【例1】在方框里填上合适的数，使算式成立。

□ 4+ 2 □8 9练习1：下面题中各图形分别表示多少？（1） 7 ☆ （2） ☆ 9 + □ 4 + 6 59 7 8 □（3） 6 △ （4） 1 ☆ 3 + △ ☆ + □ ☆9 7 1 9 5【例2】猜一猜，每个汉字各表示什么数字？学 学— 4 生8学=（ ） 生=（ ）练习2: 想一想，每个汉字和图形各表示什么数字？（1）我爱 4—学数学我=（）爱=( )数=（）学=（）（2）☆○☆—☆☆7 9 0☆=( ) ○=( )（3） 8 5 4—○○○○○○=( )【例3】在□里填合适的数，使算式成立。

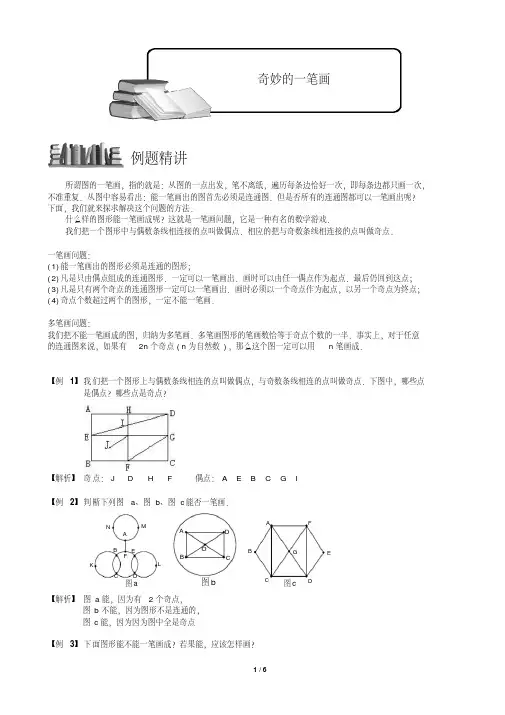
所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，不准重复．从图中容易看出：能一笔画出的图首先必须是连通图．但是否所有的连通图都可以一笔画出呢？下面，我们就来探求解决这个问题的方法．什么样的图形能一笔画成呢？这就是一笔画问题，它是一种有名的数学游戏．我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点．一笔画问题：(1)能一笔画出的图形必须是连通的图形；(2)凡是只由偶点组成的连通图形．一定可以一笔画出．画时可以由任一偶点作为起点．最后仍回到这点；(3)凡是只有两个奇点的连通图形一定可以一笔画出．画时必须以一个奇点作为起点，以另一个奇点为终点；(4)奇点个数超过两个的图形，一定不能一笔画．多笔画问题：我们把不能一笔画成的图，归纳为多笔画．多笔画图形的笔画数恰等于奇点个数的一半．事实上，对于任意的连通图来说，如果有2n 个奇点(n 为自然数)，那么这个图一定可以用n 笔画成．【例1】我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点．下图中，哪些点是偶点？哪些点是奇点？【解析】奇点：J D H F 偶点：A E B C G I【例2】判断下列图a 、图b 、图c 能否一笔画．图a NM L KFD E C BA图b O D CB A 图c G F E DC B A 【解析】图a 能，因为有2个奇点，图b 不能，因为图形不是连通的，图c 能，因为因为图中全是奇点【例3】下面图形能不能一笔画成？若果能，应该怎样画？例题精讲奇妙的一笔画【解析】图1能因为图中全是偶点，图2能因为图中全是偶点，图3不能因为有4个奇点．【例 4】下面的图形，哪些能一笔画出？哪些不能一笔画出？【解析】第1个能，2、3不能【例5】下图中不能一笔画成，请你在下图中添加最少的线段，将其改成一笔画的图形，并画出路线图．【解析】不能一笔画出，因为图中有E H G F四个奇点，连结EH就可以使图形一笔画出．【例6】下图中的线段表示小路，请你仔细观察，认真思考，能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁？该怎样爬？【解析】要想不重复爬出，需要图形能一笔画出，由于图中有两个奇点，所以应该从奇点出发才能一笔画出图形，所以甲蚂蚁能够．【例7】能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形？【解析】可以．【例8】下图是儿童乐园的道路平面图，要使游客走遍每条路并且不重复，那么出、入口应设在哪里？【解析】要想不重复，需要路线能一笔画出，由于图中有两个奇点，所以入口和出口应该分别放在两个奇点出，即F 和I 点．【例9】邮递员叔叔向11个地点送信一次信，不走重复路，怎样走最合适？【解析】不走重复路，一笔能画出路线图，图中有2个奇点，应该从奇点处出发，下面有一种参考路线：4-1-2-5-8-9-6-10-11-7-4-3【例10】观察下面的图，看各至少用几笔画成？【解析】图(1)有8个奇点，所以要4笔画出，图(2)有12个奇点，所以要一笔画出，图(3)能一笔画出．【例11】判断下列图形能否一笔画．若能，请给出一种画法；若不能，请加一条线或去一条线，将其改成可一笔画的图形．I H G F E D CB A图a H G I K L J F ED CB A图b D C H G E F B A 图c【解析】图(1)不能一笔画出，因为图中有4个奇点，连结BD ，或者去掉BF 都可以使图形能一笔画出．图(2)不能一笔画出，因为图中有4个奇点，去掉KL ，或者BK 都可以使图形能一笔画出．图(3)不能一笔画出，因为图中有4个奇点，去掉AB 可以使图形能一笔画出．一个K (K ＞1)笔画最少要添加几条连线才能变成一笔画呢？我们知道K 笔画有2K 个奇点，如果在任意两个奇点之间添加一条连线，那么这两个奇点同时变成了偶点．如左下图中的B ，C 两个奇点在右下图中都变成了偶点．所以只要在K 笔画的2K 个奇点间添加(K-1)笔就可以使奇点数目减少为2个，从而变成一笔画．【例12】18世纪的哥尼斯堡城是一座美丽的城市，在这座城市中有一条布勒格尔河横贯城区，这条河有两条支流在城市中心汇合，汇合处有一座小岛A 和一座半岛D ，人们在这里建了一座公园，公园中。

【精品】如果用笔在纸上连续不断，又不重复，一笔画成某种图形，那么这种图形就叫做一笔画.没有连成一体的图形叫做不连通图，如“吕”、“品”字图等；连成一体的图形叫做连通图，如“串”字图等.任何图形都是由点和线组成的.图形中的点可以分成两类：凡是从一个点出发的线的数目是偶数的，这个点称为偶点.凡是从一个点出发的线的数目是奇数的，这个点称为奇点.一笔画的基本规律：能一笔画出的图形必须是连通的；凡是只由偶点组成的连通图形，一定可以一笔画，画时可以由任一偶点为起点，最后仍回到这点；凡是只有两个奇点的连通图形，一定可以一笔画，画时必须以一个奇点为起点，以另一个奇点为终点；奇点的个数一定为偶数，奇点个数超过两个的图形不能一笔画，所需的最少笔数等于奇数点的个数除以2.判断下列图形能否一笔画，如果能，试着将它们画出来.解析：能够一笔画的字有：口，中，日；能够一笔画的图形有，。

标出下列各个图形各结点的奇偶性，并判断它们能否一笔画.解：各结点奇偶性如下图所示：1 422234441133332222444433211222能够一笔画的有图1、2、4.标出下列各个图形各结点的奇偶性，并判断它们能否一笔画.解：能够一笔画的有图3、4.在六面体的顶点B和E处各有一只蚂蚁(见下图)，它们比赛看谁能爬过所有的棱线，最终到达终点D.已知它们的爬速相同，哪只蚂蚁能获胜？解析：大多同学可能看不出这是一笔画问题，但利用一笔画的知识，能非常巧妙地解答这道题.这道题只要求爬过所有的棱，没要求不能重复.可是两只蚂蚁爬速相同，如果一只不重复地爬遍所有的棱，而另一只必须重复爬某些棱，那么前一只蚂蚁爬的路程短，自然先到达D点，因而获胜.问题变为从B到D与从E到D哪个是一笔画问题.图中只有E，D两个奇点，所以从E到D可以一笔画出，而从B到D 却不能，因此从E点爬的蚂蚁获胜.下图是一个公园的平面图，要使游客走遍公园每条路而不重复，问出入口应设在哪里？HGFED CBA解析：本题实际上是问这个图以哪点为起点与终点的问题，观察上图可以发现，图中只有两个“奇点”B与E，因此出入口应设在B点与E点，即这两点其中一个设为入口，则另一个设为出口.下列各图至少要用几笔才能画成？解析：对于任意连通图来说，如果有n2个奇点（n为自然数），那么这个图一定可以用n笔画成。

一笔画黄柱良 网上收集【知识要点】1．概念：一笔画是指笔不离开纸，而且每条线都只画一次不准重复而画成的图形。

2．分类：图中的点可分两大类：（1）双数点：从这点出发的线的数目是双数的，叫双数点。

（2）单数点：从这点出发的线的数目是单数的，叫单数点。

3．规律：一个图形能否一笔画成，关键在于图中单数点的多少。

（1）凡是图形中没有单数点的一定可以一笔画成。

（2）凡是图形中只有两个单数点，一定可以一笔画成，画时必须从一个单数点为起点，最后以另一单数点为终点。

（3）凡是图形中单数点的个数多于两个时，此图肯定是不能一笔画成。

【题目】1 判断下面图形中哪些点是单数点哪些点是双数点。

2 下列图形中各有几个单数点？能一笔画成吗？3 判断下面图形能不能一笔画成？如果能，应该怎样画？DBCDEFCBCA4下面图形能不能一笔画成？这什么？5 如图是一个大型花池中小路的平面图，你能否不重复地一次走完所有的小路？进出口应设在什么地方？6 将下图加上最少的线改成一笔画的图形。

7．将下图去掉最少的线改成一笔画图形。

8．下图中的线段代表小路，请小朋友想一想，能够不重复地爬遍小路的甲蚂蚁还是乙蚂蚁？该怎么爬？9．为迎接2008年奥运会在北京召开，你能一笔画出奥运会的五环图案吗？10．下图是一个公园的平面图，应怎样走才能使游客走通每条路而不重复，设计一条最佳路线。

11 一个公园的平面图如下，请你设计好入口、出口，并给出一条浏览路线，要求走遍每一条路且不重复。

12．如图，是一个公园的平面图，请你设计好入口、出口，并给出一种游玩路线，要求走遍每一条路且不重复。

13．如图，是一个名画展厅的平面图，要使参观者不重复地走遍每一条画廊，问：出口、入口应设在哪里？14．黑色的鱼与白色的鱼所能游动的河道如下图所示。

黑色的鱼在A 点位置，白色的鱼在B 点位置。

哪条鱼能不重复地游遍所有的河道？A BHC GFED15．能用一根铁丝弯成下面的图形吗？16．一个邮递员投递信件要走的街道如图，为节约时间，他想自己设计一条线路，可以不重复的走遍每一条街道，你能帮帮他吗？17．一只蚂蚁要想不重复的爬遍每一条线路，应从哪里出发，到哪里结束？18．你能用一笔画成4条线段把下图的9个点都连起来吗？19．下图能否一笔画成？如果能，应怎样画？20．如图，在一个六面体的顶点A 和B 处各有一只蜗牛，它们比赛看谁能不重复地爬遍每一棱线到达C 点。

判断一笔画的方法
判断一笔画的方法有很多，以下是其中几种常见的方法：
1. 观察画的形状和连通性：一笔画应该是一个连通的形状，如果有分支或者断开的地方，那么就不是一笔画了。

2. 计算每个点的度数：在一笔画中，每个点的度数应该都是偶数，如果存在一个或多个点的度数是奇数，那么就不是一笔画。

3. 使用欧拉公式：欧拉公式是一个用于计算平面图中点、边和面的数量关系的公式，对于一笔画来说，它的欧拉公式是F=E+2，其中F为面的数量，E为边的数量，如果符合这个公式，那么就是一笔画。

4. 通过试错法：如果以上方法都无法判断一笔画的话，可以尝试使用试错法，也就是从一个点开始画线，然后尽可能地连通所有的点，如果中途发现无法继续画下去，那么就返回上一步重新尝试，直到成功为止。

无论哪种方法，都需要注意观察和耐心尝试，才能准确地判断一笔画。

- 1 -。

三年级奥数专题：一笔画(一)如果一个图形可以用笔在纸上连续不断而且不重复地一笔画成，那么这个图形就叫一笔画。

显然，在下面的图形中，(1)(2)不能一笔画成，故不是一笔画，(3)(4)可以一笔画成，是一笔画。

同学们可能会问：为什么有的图形能一笔画成，有的图形却不能一笔画成呢？一笔画图形有哪些特点？关于这个问题有一个著名的数学故事——哥尼斯堡七桥问题。

哥尼斯堡是立陶宛共和国的一座城市，布勒格尔河从城中穿过，河中有两个岛，18世纪时河上共有七座桥连接A，B两个岛以及河的两岸C，D(如下图)。

所谓七桥问题就是：一个散步者要一次走遍这七座桥，每座桥只走一次，怎样走才能成功？当时的许多人都热衷于解决七桥问题，但是都没成功。

后来，这个问题引起了大数学家欧拉(1707-1783)的兴趣，许多人的不成功促使欧拉从反面来思考问题：是否根本就不存在这样一条路线呢？经过认真研究，欧拉终于在1736年圆满地解决了七桥问题，并发现了一笔画原理。

欧拉是怎样解决七桥问题的呢？因为岛的大小，桥的长短都与问题无关，所以欧拉把A，B两岛以及陆地C，D用点表示，桥用线表示，那么七桥问题就变为右图是否可以一笔画的问题了。

我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点。

如下图中，A，B，C，E，F，G，I是偶点，D，H，J，O是奇点。

欧拉的一笔画原理是：(1)一笔画必须是连通的(图形的各部分之间连接在一起)；(2)没有奇点的连通图形是一笔画，画时可以以任一偶点为起点，最后仍回到这点；(3)只有两个奇点的连通图形是一笔画，画时必须以一个奇点为起点，以另一个奇点为终点；(4)奇点个数超过两个的图形不是一笔画。

利用一笔画原理，七桥问题很容易解决。

因为图中A，B，C，D 都是奇点，有四个奇点的图形不是一笔画，所以一个散步者不可能不重复地一次走遍这七座桥。

顺便补充两点：(1)一个图形的奇点数目一定是偶数。

因为图形中的每条线都有两个端点，所以图形中所有端点的总数必然是偶数。

图形规律中的一笔画考点在公职考试中，图形推理作为必考模块重要性不言而喻。

但是，图形推理由于考点多且零散，考查形式又灵活多变，一直是考试的难点。

在这一次，我们重点向大家介绍图形规律中非常重要、近年来考查比重很大的一个考点：一笔画规律。

一、什么是一笔画规律所谓一笔画规律：图形能够不间断、不重复地用一笔从头画到尾，即为一笔画图形。

比如圆这个图形，能够从头到尾不间断、不重复地一笔画下来，它就是一笔画图形。

一个简单的图形，我们可以比较轻松的判断是否是一笔画图形，但是考试中，如果遇到复杂图形（如下图），如何能快速判断它最少能用几笔画出来呢？二、判断方法：数奇点奇点，就是从交点引出的线段的数目为奇数。

比如下图的A点，经过A点引出来的线段有3条，故A是奇点；经过B点引出来的线段有2条，故B不是奇点。

要注意：端点也是奇点。

如果一个图形的奇点数为0或2，则此图形最少能够一笔画画出。

如果一个图形的奇点数超过2，则用到了笔画数判断公式：笔画数=奇点数/2。

比如一个图形的奇点数是4，则最少笔画数为4/2=2。

要注意，奇点数只能为偶数个。

三、题型识别一笔画题型有典型的图形特征：（1）五角星，一笔画图形（2）“田”字变形，两笔画图形（3）圆相切，一笔画图形四、练习1.从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性：【答案】D【解析】本题考查一笔画。

题干图形组成各异，优先考虑数量规律。

观察发现，图1是五角星，考虑笔画数。

题干图形均为一笔画图形，A项为三笔画，B项为三笔画，C项为两笔画，D项为一笔画。

因此，本题答案为D。

2. 把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是：A：①②③，④⑤⑥B：①②④，③⑤⑥C：①③⑤，②④⑥D：①③⑥，②④⑤【答案】B【解析】本题考查一笔画。

组成元素不同，优先考虑数量类或属性类。

第二个图形是常考的两笔画图形的变形图形，考虑笔画数。

图形①②④均有四个奇点，为两笔画图形；图形③⑤⑥均为一笔画图形，分为两组。

第27讲一笔画图形 一笔画的理论是由大数学家欧拉（Euler）建立的.他在建立这一理论的过程中方法新颖、独特，使人们折服、倾倒.并且为人类思想宝库奉献了一颗耀眼的珍珠，这颗珍珠将在人类的智慧史上放射着不灭的光辉. 同学们，你肯定想知道什么是一笔画吧？让我们从一个游戏开始.　问题27.1图27－1中有四个图形，你能一笔画出来吗？ 这就是一笔画问题.对以上四个图，经过几次试画读者不难发现：图（1）可一笔画成且从任一点出发均可回到出发点；图（2）可一笔画成但起点只能在D或B点且不能回到出发点；图（3）、（4）均不能一笔画成. 如果一个图形可以用笔不离纸且每条线都画到并不准重复，则这个图形就叫做一笔画图形. 关于一笔画问题有下面几个问题需要解决： （1）怎样简单地判断一个图形能否一笔画？ （2）如果能一笔画，什么时候可回到出发点，什么时候又不能？ （3）对不能回到起点的一笔画，应把何处作为起点？何处作为终点？ （4）若一个图形不能一笔画，那么至少需要几笔画成？ 当图形较简单时（如图27－1），只要进行几次“试画”，就可以回答上述所有问题.但是，当图形较复杂时，要回答上述问题难度就大了. 同学们不信可以试试，如果你不看下文就能独立地解决这个问题，那么在这一问题上你就与大数学家欧拉一样聪明了. 下面我们开始研究一笔画问题. 让我们从产生这一问题的历史背景谈起吧！说起来还有一段引人入胜的故事呢！ 事情发生在公元18世纪普鲁士的哥尼斯堡城.一条河从这个城市穿过，河中有两个小岛把主流分成了两半.河上有七座桥连接两岛同河的两岸沟通（如图27－2）.这是个风景秀丽的地方，吸引了许多游人.人们在这里参观、散步.不知谁最先提出了一个问题：一个散步者怎样能一次走遍这七座桥，最后又回到出发点，而每座桥只走过一次，不许重复. 这一问题似乎不难，谁都愿意试一试，但没有一个胜利者.这下引起了许多优秀人才极大的兴趣和好奇心. 过了很久一段时间，这件事被瑞士大数学家欧拉知道了.欧拉头脑比较冷静，千百人的失败，使欧拉猜想：也许那样的走法根本不存在.经过艰辛的探索以后，他于1736年在圣彼得堡科学院作了一次报告，终于向人们解开了“七桥问题”之谜，并彻底地解决了一笔画的所有问题. 下面让我们来看看欧拉是怎么解决这一问题的，从而欣赏一下这位数学泰斗精彩绝妙的数学思维. 欧拉在对图形进行了深入细致的研究之后，发现任何图都是由点和线组成的.他把图中的点分成两类：若从一点发出的线的整目是偶数，就称为一个偶点，若是奇数就称为奇点.如图27－3，除B、J、D、F是奇点外，其它均为偶点.欧拉认为，分开的图形显然是不能一笔画的［如图27－1（4）］.一个连在一起的图（叫连通图），能不能一笔画与此图形中奇点的个数有关. 通过试画及进一步的研究欧拉认识到：研究一笔画问题时，如果我们细心地把所有可能的画法列成表格，可以逐一检查哪些（如果有的话）是满足要求的.然而这种解法太乏味且太困难了.因为可能的组合数目太大，而对于别的线数更多的图根本就不能用.如按照这样的办法分析就要引出许多与问题无关的枝节，这无疑是这种方法麻烦的原因.因此必须放弃它，去寻求另一种更专用、更本质、更广泛实用的简单方法. 欧拉先假定一个图形已经一笔画成，再考察其特点：它一定有一个起点B，一个终点E和一些中间点mi（图27－4）. （1）首先可断言所有中间点mi必为偶点，因为每次有一条线画进mi必有一条从mi画出的线与之配对. （2）如果B不与E重合，则B、E必为奇点.事实上，我们先从B画出去，即使中途画进B点，最后还是要画出去，所以画出B点的线总比画进来的线多一条，因而B是奇点.同样E也为奇点. （3）如果B与E重合，则B（即E）必为偶点.这是因为进、出B点的线一样多. 反过来可以证明：凡具备条件（1）、（2）、（3）的图形均可一笔画. 由此欧拉就得到了下面的结论：一笔画定理若一个连通图形奇点的个数为0或2时，其图形必为一笔画（反之亦然）.而且（1）当奇点个数为0时，可以取任一（偶）点为起点，最后仍回到这一点；（2）当奇点个数为2时，必须以一个奇点为起点，另一个奇点为终点. 应特别注意：欧拉解决这一问题时用的思维技巧是从结果入手考虑.人们称它为倒推法.问题27.2图27－5中的几个图形是否可一笔画？解图（1）中全为偶点.故可以一笔画. 图（2）中有6个奇点，故不能一笔画. 图（3）中有2个奇点，故可以一笔画. 到此，我们已圆满地回答了开始提出的问题（1）、（2）、（3），关于问题（4）有以下结论： 多笔画定理有2n（n＞1）个奇点的连通图形，可以用n笔画完（彼此无公共线），而且至少要n次画完.问题27.3图27.3 图27－3和27－5（2）分别要几笔画完？ 理论的目的在于应用.和其它数学理论一样，一笔画是一种数学模型，要把它应用于实际，还必须学会把实际问题抽象、转化成这种模型.问题27.4图27.4图27－6是一个公园的平面图，要使游客走遍每条路且不重复，问出、入口应设在哪里？解本问题相当于一笔画问题. 由于图中有两个奇点，由一笔画定理，只要将出、入口分别设在D、I两点，游客就可以从入口进入公园，不重复地走遍所有小径，而最后从出口处离开公园.问题27.5能否一笔画出一条线路，使它和图27－7的8条线段都相交且仅相交一次（并不在端点处相交）？分析本题的实质并不是研究图27－7本身的一笔画问题，而是研究图中虚线表达的图的一笔画问题.解图27－7中的8条实线段，把平面分成了5个部分，而把每个部分看成一个点，用①、②、③、④、⑤表示.那么画一条线与8条线段都只相交一次就相当于把这5个数字两两相连.从而原问题就转化成了图27－7中虚线图形的一笔画问题. 因为虚线图有4个奇点（①、②、③、④），由多笔画定理，它至少得2笔画成. 注意：本题的关键（题眼）是把5块区域看成5个点，从而把实际问题抽象成一笔画的问题. 下面我们再运用这种方法来解决著名的“七桥问题”.问题27.6一个散步者能否一次走遍图27－8（1） 所示的七座桥且不许重复？解河流把地平面分成四个区域A、B、C、D，把这四个区域看成四个点.每两块区域之间有一座桥相通就相当于在相应的两点之间连一条线段，这样我们就把七桥问题抽象成了图27－8（2）的一笔画问题.因为本图有四个奇点，故原题中散步者的散步路线是不存在的.问题27.7图27－9（1）是某展览馆的平面图.每个房间都有一扇门通往馆外，每相邻两个房间之间各有一扇门相通.参观者能不能一次无重复地穿过每一扇门？如不能，关闭哪一扇门后就能无重复地穿过每一扇门了？并问出、入口在哪里？解本问题第一问与问题27.5、27.6解法相类似.5个展室加馆外，相当于6个区域，分别用①～⑥表示.把它们看成6个点，用一线段表示一扇门，就可得到图27－9（2）.此图有③、④、⑤、⑥4个奇点，所以不能一笔画成.即表明，参观者要想不重复地穿过每一扇门是不可能的. 第二问实际上是问在图（2）中去掉哪一段线就能使图形一笔画出.由于③、④、⑤、⑥均为奇点，只要关闭③、④之间的一扇门，就只剩下⑤、⑥两个奇点了.这时，只要把⑤、⑥分别当做出、入口，参观者就可以不重复地一次穿过其余各门了. 同样地，从图中易看出，关闭④、⑤，或⑤、⑥，或④、⑥，或③、⑥之间的任一扇门，参观者也可以如愿以偿. 我们还可以证明：在一个图中奇点的个数必定是偶数. 从本题的解法我们不难看到：在两个奇点之间去掉一条连线，这两个奇点就同时变为偶点.同样，在两个奇点之间增加一条连线，也可使这两个奇点同时成为偶点.问题27.8在奇点和偶点之间连一条线后，图中的奇、偶点个数有什么变化？ 以上讲了许多一笔画知识，也许学过后一些肯动脑筋的同学可能会想：一笔画知识除了做数学游戏外，还有什么实用价值呢？为了回答这个问题我们先介绍几个名词： 对一个连通图，通常把从某点出发一笔画成所经过的路线叫做欧拉路；把一笔画成回到出发点的欧拉路叫欧拉回路；具有欧拉回路的图叫做欧拉图. 现在城市的街道及公园、展馆的参观路线，严格地说来大多数都设计得杂乱无章.人们上、下班，参观游览，邮递员送信及各种车辆行驶都要走许多重复的路，且会漏掉许多事物.这样不但消耗了许多不必要的财力，而且浪费了大量的时间. 同学们，你们学了一笔画知识后，就可以当未来世界的设计师，把未来的城市街道设计成某种欧拉回路，并把公园、展馆设计成欧拉路.到那时，投递员叔叔再送邮件时，就可一次跑完所有街道最后回到邮局；人们参观公园只需走一趟就会对所有内容一览无余.在你们的劳动下，世界将会变得更美好.练习27 1.图27－10中的三个图形分别能用几笔画成？若能一笔画能否回到起点？ 2.图27-11能否一笔画？若不能，你能用什么办法使它成为一笔画？ 3.用剪刀能否一次连续剪下图27－12所示的纸片上的三个正方形和二个三角形？如能，怎么剪？ 4.图27-13是一座古籍展品馆，每两个相邻的展室之间都有一扇门相通.除中间的展室E外，每个展室都有门通向室外.如果你去参观，你如何设法使自己不重复地穿过每一道门？ 5.图27-14是蓬莱仙境区某处的地貌图，小河上有15座桥.问能不能设计一条路线，一次不重复地走遍所有的桥？。