一笔画成的图形

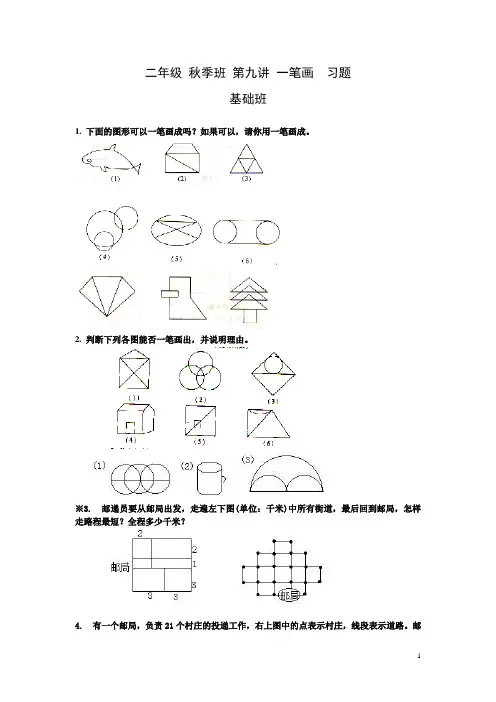
二年级秋季班第九讲一笔画习题基础班1. 下面的图形可以一笔画成吗？如果可以，请你用一笔画成。

2. 判断下列各图能否一笔画出，并说明理由。

※3. 邮递员要从邮局出发，走遍左下图(单位：千米)中所有街道，最后回到邮局，怎样走路程最短？全程多少千米？4. 有一个邮局，负责21个村庄的投递工作，右上图中的点表示村庄，线段表示道路。

邮递员从邮局出发，怎样才能不重复地经过每一个村庄，最后回到邮局？5. 一只木箱的长、宽、高分别为5，4，3厘米(见右图)，有一只甲虫从A点出发，沿棱爬行，每条棱不允许重复，则甲虫回到A点时，最多能爬行多少厘米？6.下图是商场的平面图，顾客可以从六个门进出商场，怎样走才能不重复地走遍商场的每条通道？7.一只蚂蚁由A点出发，到达B点，必须不重复地经过每一条线，你能想出好办法吗？8.一辆清洁车清扫街道，每段街道长1千米，清洁车由A点出发，走遍所有的街道再回到A点，怎样走路程最短，全程多少千米？9.游人在林间小路上（见图）散步，问能否一次不重复地走遍所有的路线后回到出发点？如不能，应选择怎样的路线才能使全程最短？最短路程是多少？（单位：千米）10.一张纸上画有如下所示的图，你能否用剪刀连续剪下图中的三个正方形和两个三角形？※11.上图是某个花房的平面图，它由六间展室组成，每相邻两室有一门相同，请你设计一个出口，使参观者能够从入口处进去，一次不重复地经过所有的门，最后由出口走出花房。

习题答案1 .2.答案略3．50千米，走法见左下图。

4.见下图。

5.最多爬行34厘米。

提示：8个点都是奇点，故至少要少爬4条棱。

少爬3厘米的棱和4厘米的棱各两条是最合理的(见右图)。

6 只有C、D两点是单数点，因此能从C门进，D门出。

或从D门进，C门出，才能不重复地走遍商场的每条通道.7 蚂蚁可以这样走：8图中有8个单数点，两个单数点之间线段要重复走，清洁车至少必须重复走4段1千米的街道，所走的路线如下图所示，全程最短路线是28千米。

苏教版二年级下册奥数第10讲一笔画成【知识概述】“一笔画”是一种常见的数学游戏。

一笔画是指笔不离开纸，并且每条线只能画一次又不重复的平面图形。

一笔能写成的字还真不少，如:1，2，3，6，7，8，9，0，一，乙，……一笔能画成的图形也不少，如那么究竟哪些图形能一笔画成呢?我们先来认识“双数点”和“单数点”。

双数点:就是从某一点出发，引出来的线的条数是双数(2，4，6，8，10，…)，这样的点就叫做双数点。

如下面的“・”都是双数点。

单数点，就是从某一点出发，引出的线的条数是单数(1，3,5,7，9，…)，这样的点就叫单数点，如下面的“・”都是单数点。

凡是图形中的点都是双数点，这个图形就一定能一笔画成。

如：凡是图形中有双数点也有单数点，但只有两个单数点，也可以一笔画成。

如凡是图形中的单数点的个数多于2个，就不能一笔画成。

如：例1：下面的图形能不能一笔画成?如果能，应怎样画?练习一：1.下面两个图形能一笔画成吗?如果能，请一笔画成功。

2.下面的图形能不能一笔画成?如果能，应怎样画?3.下面的图形能不能一笔画成?为什么?例2：下面的图形能不能一笔画成?如果能，应该怎样画?练习二：1.下面的图形能不能一笔画成?如果能，应该怎样画?如果不能，请说明理由。

2.下面的图形能不能一笔画成?如果能，应该怎样画?3.下面的图形能不能一笔画成?如果能，应该怎样画?例3：有一条河，河中有两个小岛，河上有7座桥，把这两个岛与河岸联系起来，能不能不重复地走遍七座桥，最后又回到出发点?练习三：1.下图是一个迷阵图，箭头指出了迷阵的入口和出口。

请你画线表示从入口进入迷阵，从出口走出来。

能不能走通?2.下图是某展览馆的平面图，相邻两个展室之间有一个门相通，每个展室都有一扇门通往馆外。

一个参观者怎样走才能不重复地走过每一扇门?如果这种走法不存在，应关闭展览室的哪扇门才能实现上述走法?3.下图中有11个邮递员的投递点，邮递员叔叔要向这11个地点送信，邮递员能不能不重复地一次走遍各个点?如果能应怎样走?例4：下面的图形中有6个单数点，因此不能一笔画成功。

一笔画问题 Company number：【WTUT-WT88Y-第三节一笔画问题从图形上的某一点出发，找出一条路线，用笔不离开纸，连续不断又不重复地经过图形上所有部分，这样画成的图形叫做一笔画。

奇数点：与奇数条线段相连的点。

偶数点：与偶数条线段相连的点。

一笔画图形有如下三条规律：1、凡是图形中没有单数点的一定可以一笔画成，画时可以从任意一个双数点为起点，最后仍回到这点，如图（1）2、凡是图形中只有两个单数点的一定可以一笔画成，画时必须从一个单数点为起点，最后以另一个单数点为终点，如图（2）3、凡是图形中单数点的个数多于两个时此图形不能一笔画成，如图（3）（1）（2）（3）解题方略：判断一幅图能否一笔画的关键1、一笔画的前提：必须是连通图；2、砍图中是否有奇点，有，有几个。

例题解析：例1、判断下面图形哪些能一笔画哪些不能一笔画说明判断依据。

（1）（2）（3）解析：图（1）能一笔画，因为它没有奇点，全为为偶点，画时从任意一个偶点起笔，终点又回到这一偶点。

图（1）能一笔画，因为它只有两个奇点，其它都为偶点，画时从一个奇点起笔到另一个奇点终点。

图（1）不能一笔画，因为它只有4个奇点，其它都为偶点。

例2、一笔画出下面每个图形。

D BE AB C EC例2-1 例2-2解析：例2-1图中有5个点，其中B、C成为奇点，只要以这两个点分别做一笔画起、终点，此图就能画出来。

下面是一种画法：DAE（起点）B C（终点）例2-2图中有5个点，其中B、C为奇点，只要以这两点分别做一笔画起、终点，此图就能画出来。

下面是一种画法：B→D→A→E→D→A→E→C→B→A→C例3、先数一数下列各图形中奇结点的个数。

如果有的图形不能一笔画成，那么，至少几笔才能画成解析：图（a）中只有两个奇结点，可从A点出发一笔画出到B点结束，图（b）中有四个奇结点，不能一笔画成。

图（b）与图（a）比较，多出了折线CEFD。

如果先一笔画出图（a），再添一笔画出折线CEFD，就可得到图（b）。

一笔画出图形
[题目］你能笔尖不离纸，一笔画出下面的每个图形吗？试试看。

（不走重复线路）
要正确解答这道题，必须弄清一笔画图形有哪些特点。

早在18世纪，瑞士的著名数学家欧拉就找到了一笔画的规律。

欧拉认为，能一笔画的图形必须是连通图。

连通图就是指一个图形各部分总是有边相连的，这道题中的三个图都是连通图。

但是，不是所有的连通图都可以一笔画的。

能否一笔画是由图的奇、偶点的数目来决定的。

什么叫奇、偶点呢？与奇数（单数）条边相连的点叫做奇点；与偶数（双数）条边相连的点叫做偶点。

如图1中的①、④为奇点，②、③为偶点。

数学家欧拉找到一笔画的规律是什么呢?
7
1．凡是由偶点组成的连通图，一定可以一笔画成。

画时可以把任一偶点为起点，最后一定能以这个点为终点画完此图。

例如，图2都是偶点，画的线路可以是：①→③→⑤→⑦→②→④→⑥→⑦→①
2．凡是只有两个奇点的连通图（其余都为偶点），一定可以一笔画成。

画时必须把一个奇点为起点，另一个奇点终点。

例如，图1图的线路是：①→②→③→①→④
3．其他情况的图都不能一笔画出。

小朋友，请试一试：
1．画出图1和图2的其他线路。

2．图3能一笔画吗？有多少条线路？
3．下图是国际奥林匹克运动会的会标，能一笔画吗？如果能，请你把它画出来。

三年级奥数专题：一笔画(一)如果一个图形可以用笔在纸上连续不断而且不重复地一笔画成，那么这个图形就叫一笔画。

显然，在下面的图形中，(1)(2)不能一笔画成，故不是一笔画，(3)(4)可以一笔画成，是一笔画。

同学们可能会问：为什么有的图形能一笔画成，有的图形却不能一笔画成呢？一笔画图形有哪些特点？关于这个问题有一个著名的数学故事——哥尼斯堡七桥问题。

哥尼斯堡是立陶宛共和国的一座城市，布勒格尔河从城中穿过，河中有两个岛，18世纪时河上共有七座桥连接A，B两个岛以及河的两岸C，D(如下图)。

所谓七桥问题就是：一个散步者要一次走遍这七座桥，每座桥只走一次，怎样走才能成功？当时的许多人都热衷于解决七桥问题，但是都没成功。

后来，这个问题引起了大数学家欧拉(1707-1783)的兴趣，许多人的不成功促使欧拉从反面来思考问题：是否根本就不存在这样一条路线呢？经过认真研究，欧拉终于在1736年圆满地解决了七桥问题，并发现了一笔画原理。

欧拉是怎样解决七桥问题的呢？因为岛的大小，桥的长短都与问题无关，所以欧拉把A，B两岛以及陆地C，D用点表示，桥用线表示，那么七桥问题就变为右图是否可以一笔画的问题了。

我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点。

如下图中，A，B，C，E，F，G，I是偶点，D，H，J，O是奇点。

欧拉的一笔画原理是：(1)一笔画必须是连通的(图形的各部分之间连接在一起)；(2)没有奇点的连通图形是一笔画，画时可以以任一偶点为起点，最后仍回到这点；(3)只有两个奇点的连通图形是一笔画，画时必须以一个奇点为起点，以另一个奇点为终点；(4)奇点个数超过两个的图形不是一笔画。

利用一笔画原理，七桥问题很容易解决。

因为图中A，B，C，D 都是奇点，有四个奇点的图形不是一笔画，所以一个散步者不可能不重复地一次走遍这七座桥。

顺便补充两点：(1)一个图形的奇点数目一定是偶数。

因为图形中的每条线都有两个端点，所以图形中所有端点的总数必然是偶数。