2019高考流程图3—新
- 格式:ppt
- 大小:650.00 KB
- 文档页数:23

聚焦高考化学工业流程题—以2019年全国各类高考试卷为例周俊清摘要:以2019年全国Ⅰ卷、全国Ⅱ卷、全国III卷、北京卷和江苏卷中的化工流程题型为研究对象,采用文献参考法、试卷研究法和统计分析法,从试题分值比重、考查知识、内容水平和核心素养等方面进行分析统计,并结合2019及部分2018高考化学真题探讨化工流程题型的特征,聚焦高考化工流程题的基本分析策略。
关键词:高考;化工流程;核心素养;分析策略化工流程题往往是以真实的工业生产过程为背景,一般以流程图的形式呈现,也有少数会以文字附带表格、图像等形式出现,化工流程题能够综合考查学生各个方面的基础知识,覆盖面较广,主要体现在考查学生获取信息的能力、分解问题的能力、应用已有知识解决实际问题的能力、表达能力等,该题型经常结合社会环境问题、资源综合开发利用等方面,要求学生要立足当下社会环境中,理性看待化工与社会生产生活的关系,强化学生的环保意识和社会责任感[1]。
本文以2019年全国Ⅰ卷、全国Ⅱ卷、全国III卷、北京卷(2018年卷)和江苏卷中的化工流程题型为研究对象,对化工流程题进行剖析,以明了工业生产流程主线与核心,掌握化工流程题的解题思路。
1. 2019年化学试卷中化工流程题分析从试题分值比重、考查知识、内容水平和核心素养等方面来研究2019年四类化学试卷及2018年北京卷中化工流程题。
1.1 高考化学化工流程题的分值比重大部分省份2019年的高考化学试卷中都会有至少一个化工流程图题,但2019年的北京卷中并没有出现我们熟悉的一般意义上的化工流程题型,其考查的四个大题目与2018年大体上没有很大变化,具体为25——有机合成,27——化学反应原理大综合考查,28——带实验装置图的探究性实验考查,而26题由18年化工流程图题型变成了19年的纯文字描述的实验题,故以18年的北京卷26题代替19年的进行分析。
大部分省份的2019年的高考化学试卷中化工流程题的分值所占比重均在12%以上,其中以全国Ⅰ卷和全国Ⅱ卷所占比例最大(见表1)。

2019年高考真题专题汇编——工业流程图专题1.(2019江苏)实验室以工业废渣(主要含CaSO 4·2H 2O ,还含少量SiO 2、Al 2O 3、Fe 2O 3)为原料制取轻质CaCO 3和(NH 4)2SO 4晶体,其实验流程如下:(1)室温下,反应CaSO 4(s)+23CO -(aq)CaCO 3(s)+24SO -(aq)达到平衡,则溶液中()()2423SO CO c c --=________[K sp (CaSO 4)=4.8×10−5,K sp (CaCO 3)=3×10−9]。
(2)将氨水和NH 4HCO 3溶液混合,可制得(NH 4)2CO 3溶液,其离子方程式为________;浸取废渣时,向(NH 4)2CO 3溶液中加入适量浓氨水的目的是________。
(3)废渣浸取在如图所示的装置中进行。
控制反应温度在60~70 ℃,搅拌,反应3小时。
温度过高将会导致CaSO 4的转化率下降,其原因是________;保持温度、反应时间、反应物和溶剂的量不变,实验中提高CaSO 4转化率的操作有________。
(4)滤渣水洗后,经多步处理得到制备轻质CaCO 3所需的CaCl 2溶液。
设计以水洗后的滤渣为原料,制取CaCl 2溶液的实验方案:______[已知pH=5时Fe(OH)3和Al(OH)3沉淀完全;pH=8.5时Al(OH)3开始溶解。
实验中必须使用的试剂:盐酸和Ca(OH)2]。
【答案】1.6×104 3HCO -+NH 3·H 2O +4NH +23CO -+H 2O(或3HCO -+NH 3·H 2O+4NH +23CO -+H 2O) 增加溶液中23CO -的浓度,促进CaSO 4的转化 温度过高,(NH 4)2CO 3分解 加快搅拌速率 在搅拌下向足量稀盐酸中分批加入滤渣,待观察不到气泡产生后,过滤,向滤液中分批加入少量Ca(OH)2,用pH 试纸测量溶液pH ,当pH 介于5~8.5时,过滤【解析】【分析】(1)反应CaSO 4(s )+CO 32-(aq )CaCO 3(s )+SO 42-(aq )的平衡常数表达式为2423c SO c CO --()(),结合CaSO 4和CaCO 3的K sp 计算; (2)氨水与NH 4HCO 3反应生成(NH 4)2CO 3;加入氨水抑制(NH 4)2CO 3的水解; (3)温度过高,(NH 4)2CO 3分解,使CaSO 4转化率下降;保持温度、反应时间、反应物和溶剂的量不变,提高CaSO 4转化率即提高反应速率,结合反应的特点从影响反应速率的因素分析;(4)根据工业废渣中的成分知,浸取、过滤后所得滤渣中含CaCO 3、SiO 2、Al 2O 3和Fe 2O 3;若以水洗后的滤渣为原料制取CaCl 2溶液,根据题给试剂,首先要加入足量盐酸将CaCO 3完全转化为CaCl 2,同时Al 2O 3、Fe 2O 3转化成AlCl 3、FeCl 3,过滤除去SiO 2,结合题给已知,再利用Ca (OH )2调节pH 除去Al 3+和Fe 3+。

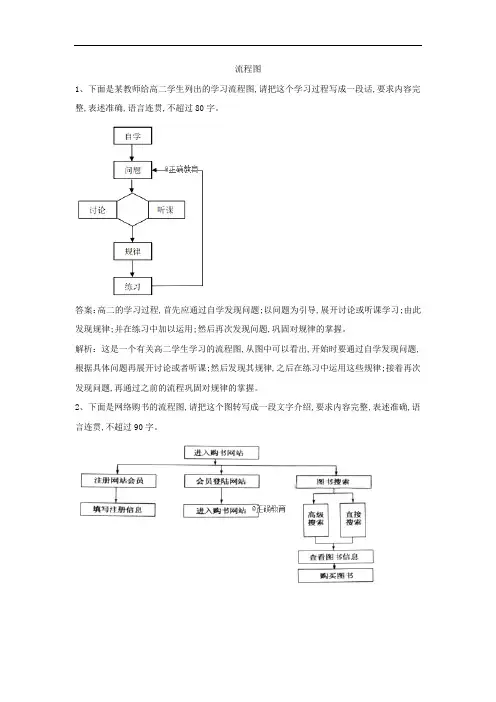
流程图1、下面是某教师给高二学生列出的学习流程图,请把这个学习过程写成一段话,要求内容完整,表述准确,语言连贯,不超过80字。
答案:高二的学习过程,首先应通过自学发现问题;以问题为引导,展开讨论或听课学习;由此发现规律;并在练习中加以运用;然后再次发现问题,巩固对规律的掌握。
解析:这是一个有关高二学生学习的流程图,从图中可以看出,开始时要通过自学发现问题,根据具体问题再展开讨论或者听课;然后发现其规律,之后在练习中运用这些规律;接着再次发现问题,再通过之前的流程巩固对规律的掌握。
2、下面是网络购书的流程图,请把这个图转写成一段文字介绍,要求内容完整,表述准确,语言连贯,不超过90字。
答案:进人购书网站之后,需要注册网站会员,填写注册信息,然后以会员的身份登陆网站进入购书网站进行图书搜索,可以选择高级搜索或直接搜索的任何一种搜索方式,查看图书信息,购买图书。
解析:3、下面是某洗衣房的工作流程图,请把这个流程图写成一段话,要求内容完整,表述准确,语言连贯,不超过60个字。
答案:工作人员先登记收费,再对衣物分拣归类,然后干洗或水洗,如不合格,需重新分类洗涤;合格后,烘干熨烫,最后配送。
解析:4、下面是公务接待流程图,请把整个流程写成一段话。
要求内容完整,表述准确,语言连贯,不超过80字。
答案:公务接待前,办公室提出申请并拟定接待方案;经局长审批确定后,办公室相关科室开展接待工作;接待结束后,办公室对接待费用进行审核结算。
解析:本题为流程图转化题。
首先,要明确各个职能部门的职责与具体分工,如办公室负责提出申请、拟定接待方案等。
其次, 要根据箭头指示明确工作流程,最后,语言表述要连贯、准确且符合题干要求。
5、下面是企业职工职称评审流程图,请把这个流程写成一段话。
要求内容完整,表述准确,语言连贯,不超过120字。
需提交的材料名称无需逐一列出。
答案:企业职工提出申请并提交评审表等材料,交由科教股初审,未通过审査的职工重新准备材料提交申请。
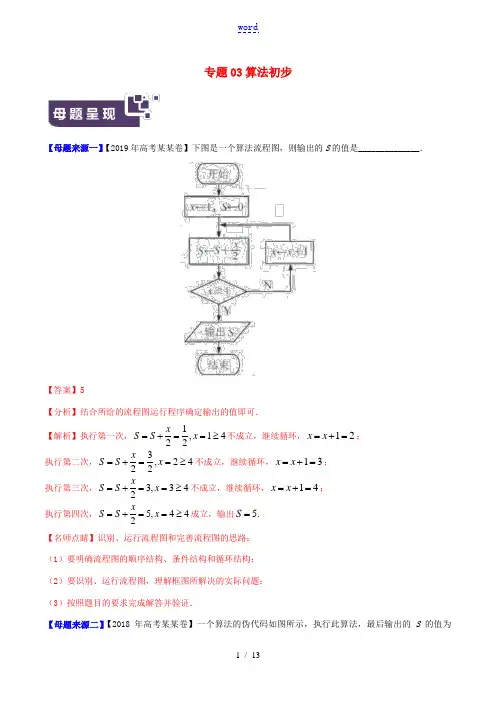
专题03算法初步【母题来源一】【2019年高考某某卷】下图是一个算法流程图,则输出的S 的值是______________.【答案】5【分析】结合所给的流程图运行程序确定输出的值即可. 【解析】执行第一次,1,1422x S S x =+==≥不成立,继续循环,12x x =+=; 执行第二次,3,2422x S S x =+==≥不成立,继续循环,13x x =+=; 执行第三次,3,342xS S x =+==≥不成立,继续循环,14x x =+=;执行第四次,5,442xS S x =+==≥成立,输出 5.S =【名师点睛】识别、运行流程图和完善流程图的思路: (1)要明确流程图的顺序结构、条件结构和循环结构; (2)要识别、运行流程图,理解框图所解决的实际问题; (3)按照题目的要求完成解答并验证.【母题来源二】【2018年高考某某卷】一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为______________.【答案】8【解析】由伪代码可得3,2;5,4;7,8I S I S I S ======, 因为76>,所以结束循环,输出8.S =【母题来源三】【2017年高考某某卷】如图是一个算法流程图,若输入x 的值为116,则输出y 的值是______________.【答案】2-【解析】由题意得212log 216y =+=-,故答案为2-. 【名师点睛】算法与流程图的考查,侧重于对流程图循环结构、条件结构和伪代码的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环的初始条件、循环次数、循环的终止条件,要通过循环规律,明确流程图研究的数学问题,是求和还是求项.【命题意图】(1)了解算法的含义,了解算法的思想.(2)理解流程图的三种基本逻辑结构:顺序、条件分支、循环.(3)理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.【命题规律】高考中对流程图的考查,主要是顺序结构、条件结构、循环结构,其中循环结构为重点,考查程序运行后的结果,或考查控制循环的条件,流程图常与函数、数列、不等式等知识点结合考查.高考中对算法语句的考查,主要是以伪代码的形式重点考查条件语句和循环语句.结合某某近几年的高考,此部分的考查基本集中在两个方面:一是流程图表示的算法;二是伪代码表示的算法.【方法总结】三种基本逻辑结构的常见问题及解题策略:(1)顺序结构顺序结构是最简单的算法结构,语句与语句之间、框与框之间是按从上到下的顺序进行的.(2)条件结构利用条件结构解决算法问题时,重点是判断框,判断框内的条件不同,对应的下一框中的内容和操作要相应地进行变化,故要重点分析判断框内的条件是否满足.(3)循环结构①已知流程图,求输出的结果.可按流程图的流程依次执行,最后得出结果.②完善流程图问题,结合初始条件和输出结果,分析控制循环的变量应满足的条件或累加、累乘的变量的表达式.③对于辨析流程图功能问题,可将程序执行几次,即可根据结果作出判断.1.【某某省某某市2018-2019学年高三考前模拟检测数学试题】某算法流程图如图所示,该程序运行后,x ,则实数a的值为_______.若输出的63【答案】7【解析】执行第一次循环时,有1n =,21x a =+; 执行第二次循环时,有2n =,43x a =+; 执行第三次循环时,有3n =,87x a =+, 此时有4n =,输出87x a =+. 所以8763a +=,故7a =. 故填7.【名师点睛】对于流程图的问题,我们可以从简单的情形逐步计算,计算时关注各变量的变化情况,并结合判断条件决定输出何种计算结果.对于本题,按流程图逐个计算后可得关于a 的方程,解出a 即可. 2.【某某省某某市2019届高三模拟练习卷(四模)数学试题】执行如图所示的伪代码,则输出的S 的值为_______.【答案】17【解析】模拟执行程序代码,可得S =3.第1步:i =2,S =S +i =5; 第2步:i =3,S =S +i =8; 第3步:i =4,S =S +i =12; 第4步:i =5,S =S +i =17. 此时,退出循环,输出S 的值为17. 故答案为17.【名师点睛】本题主要考查了循环结构的程序代码,正确依次写出每次循环得到的i ,S 的值是解题的关键,属于基础题.求解时,模拟执行程序代码,依次写出每次循环得到的i ,S 的值,即可得解输出的S 的值.3.【某某省某某市2019届高三适应性考试数学试题】一个算法的流程图如图所示,则输出的a 的值为_______.【答案】9【解析】初始值1,0n a ==,第一步:033,1124a n =+==+=<,继续执行循环; 第二步:336,2134a n =+==+=<,继续执行循环; 第三步:639,314a n =+==+=,结束循环,输出9a =. 故答案为9.【名师点睛】本题主要考查程序框图,分析框图的作用,逐步执行,即可得出结果.4.【某某省某某金陵中学、海安高级中学、某某外国语学校2019届高三第四次模拟考试数学试题】如图是一个算法流程图,则输出的b 的值为_______.【答案】8【解析】第1步:a>10不成立,a=a+b=2,b=a-b=1;第2步:a>10不成立,a=a+b=3,b=a-b=2;第3步:a>10不成立,a=a+b=5,b=a-b=3;第4步:a>10不成立,a=a+b=8,b=a-b=5;第5步:a>10不成立,a=a+b=13,b=a-b=8;第6步:a>10成立,退出循环,输出b=8.故答案为8.【名师点睛】本题考查循环结构的程序框图,对循环体每次循环需要进行分析并找出内在规律,属于基础题.对于本题,根据程序框图,写出每次运行结果,利用循环结构计算并输出b的值.5.【某某省七市(某某、某某、某某、某某、某某、宿迁、某某)2019届高三第三次调研考试数学试题】如图是一个算法流程图.若输出y的值为4,则输入x的值为_______.【答案】−1【解析】当1x ≤时,由流程图得:3y x =-, 令34y x =-=,解得:1x =-,满足题意. 当1x >时,由流程图得:3y x =+, 令34y x =+=,解得:1x =,不满足题意. 故输入x 的值为1-.【名师点睛】本题主要考查了流程图知识,考查分类思想及方程思想,属于基础题.求解时,对x 的X 围分类,利用流程图列方程即可得解.6.【某某省苏锡常镇四市2019届高三教学情况调查(二)数学试题】根据如图所示的伪代码,最后输出的i 的值为_______.【答案】8【解析】根据如图所示的伪代码得:1T =,2i =,6T <成立,212T =⨯=,224i =+=; 6T <成立,224T =⨯=,426i =+=;6T <成立,428T =⨯=,628i =+=, 6T <不成立,结束循环,输出8i =.故答案为8.【名师点睛】本题主要考查了循环结构语句及其执行流程,属于基础题.按程序图依次执行即可得解. 7.【某某省某某市2019届高三下学期4月阶段测试数学试题】执行如图所示的伪代码,若输出的y 的值为13,则输入的x 的值是_______.【答案】8【解析】输出13y =,若6y x =,则1326x =>,不合题意; 若5y x =+,则1358x =-=,满足题意. 本题正确结果为8.【名师点睛】本题考查算法中的If 语言,属于基础题.根据伪代码逆向运算求得结果.8.【某某省某某中学2019届高三3月月考数学试题】执行如图所示的伪代码,最后输出的a 的值为_______.【答案】4【解析】模拟执行程序代码,可得i =1,a =2,满足条件i 2≤,执行循环体,a =1⨯2,i =2; 满足条件i 2≤,执行循环体,a =1⨯22⨯,i =3, 不满足条件i 2≤,退出循环,输出a 的值为4. 故答案为4.【名师点睛】本题主要考查了循环结构的程序框图,正确依次写出每次循环得到的i ,a 的值是解题的关键,当i =3时,不满足条件退出循环,输出a 的值即可,属于基础题.9.【某某省某某市(苏北三市(某某、某某、某某))2019届高三年级第一次质量检测数学试题】运行如图所示的伪代码,则输出的结果S 为_______.【答案】21【解析】第1步:3,9I S ==; 第2步:5,13I S ==; 第3步:7,17I S ==;第4步:9,21I S ==,退出循环,输出21S =. 故答案为21.【名师点睛】本题考查的知识点是程序框图和语句,当循环的次数不多或有规律时,常采用模拟循环的方法解答.求解时,由已知中的程序代码可得:程序的功能是利用循环结构计算并输出变量S 的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.10.【某某省某某市2019届高三下学期阶段测试数学试题】根据如图所示的伪代码,可知输出的结果为_______.【答案】205【解析】阅读伪代码可知,I 的值每次增加2,23S I =+, 跳出循环时I 的值为101I =,输出的S 值为21013205S =⨯+=. 故答案为205.11.【某某省某某市2019届高三5月高考信息卷数学试题】执行如图所示的程序框图,输出的k 的值为_______.【答案】7【解析】程序执行中的数据变化如下:1,3,k S ==133,123S k =⨯==+=, 继续运行,339,325S k =⨯==+=;继续运行,9545,527S k =⨯==+=,S >10,此时退出循环,输出k =7, 故答案为7.12.【某某省高三某某中学、宜兴中学、梁丰2019届高三第二学期联合调研测试数学试题】中国南宋时期的数学家秦九韶提出了一种多项式简化算法,如图是实现该算法的程序框图,若输入的2n =,1x =,依次输入的a 为1,2,3,运行程序,输出的s 的值为_______.【答案】6【解析】第一次输入1a =,得1s =,1k =,判断否;第二次输入2a =,得3s =,2k =,判断否;第三次输入3a =,得6s =,3k =,判断是,退出循环,输出6s =,故答案为6.【名师点睛】本题考查了循环结构流程图,要注意每次循环后得到的字母取值,属于基础题.求解时,先代入第一次输入的a ,计算出对应的,s k ,判断为否,再代入第二次输入的a ,计算出对应的,s k ,判断仍为否,再代入第三次输入的a ,计算出对应的,s k ,判断为是,得到输出值.13.【某某省某某市、某某市2019届高三第二次模拟考试数学试题】下图是某算法的伪代码,输出的结果S的值为_______.【答案】16【解析】运行结果依次为:i =1,S =1,1<6,i =3,S =4;3<6,i =5,S =9;5<6,i =7,S =16,7>6,输出S =16.故答案为16.【名师点睛】本题主要考查算法,意在考查学生对该知识的理解能力和掌握水平.直接按照算法的伪代码运行即得结果.14.【某某省某某市基地学校2019届高三3月联考数学试题】运行如图所示的流程图,若输入的63a b ==,,则输出的x 的值为_______.【答案】0【解析】由6a =,3b =得:3x =,循环后:4b =,5a =;由4b =,5a =得:1x =,循环后:2b =,4a =;由2b =,4a =得:2x =,循环后:3b =,3a =;由3b =,3a =得:0x =,输出结果:0x =,本题正确结果为0.【名师点睛】本题考查程序框图中的条件结构和循环结构,属于基础题.求解时,按照程序框图依次运算,不满足判断框中条件时输出结果即可.15.【某某省某某、某某、某某、苏北四市七市2019届高三第一次(2月)模拟数学试题】如图是一个算法流程图,则输出的b 的值为_______.【答案】7【解析】初始值:a =0,b =1.第1次循环:a =1,b =3,满足a <15;第2次循环:a =5,b =5,满足a <15;第3次循环:a =21,b =7,不满足a <15,退出循环,输出b =7.故答案为7.【名师点睛】本题考查的知识点是算法流程图,由于循环的次数不多,故可采用模拟程序运行的方法进行.。



专题03 实验装置图及提纯流程图题【19年高考命题前瞻】化学作为一门实验科学,实验考查是高考必考内容,高考中高频考点主要有:(1)化学实验常用仪器的识别和用途。
(2)化学实验基本操作及实验安全。
(3)物质的分离、提纯及鉴别(科学探究与创新意识)。
主要有以下两种题型进行考查:(1)选择题:化学实验基础知识一直是高考命题的热点,选择题主要考查化学实验基础知识,仪器的使用、实验装置图的正误判断,分离提纯物质的方法等,在近几年的高考试题中呈现率较高,每个选项从不同角度拼盘式考查化学实验常用仪器的主要用途和使用方法,化学实验的基本操作规范;各选项具有一定的独立性,题目比较简单,多以表格的形式出现。
(2)非选择题:常以综合实验设计题或工艺流程图题为情景,将实验原理与元素化合物知识相结合,考查实验操作、实验现象的解释与评价等,题干主要以图表的形式提供信息,根据信息进行分析解答。
预计2019年高考中仍以这两种题型出现,与新材料、新实验方法相结合考查实验基础和实验综合知识。
由于对图表中信息分析不到位导致错解的情况很多,【名师精讲】一、实验试题的命题特点1、实验基础试题所考查的重点是实验基本操作技能。
这类试题的特点通常是给出限定的仪器、药品和一些操作步骤,判断实验的原理、操作、现象及结论是否正确,既有常见仪器的使用,又有正确操作的辨别。
两种形式都重在考查考生的实验基本操作技能,其中,物质的分离和提纯、离子检验或物质鉴别是高考的必考点,主要考查常见离子的检验方法以及常见物质的鉴别方法,能根据不同条件选择不同的检验方法。
物质的分离和提纯是实验题及工艺流程题必然出现的环节,高考中可以单独以图表形式的选择题考查,也可以在综合实验题或工艺流程题中考查。
2、高考综合实验题的命题特点:知识容量大、出题素材新、考查角度广、综合程度高。
纵观近几年全国卷中的综合实验题:①涉及的题型有物质制备实验题、性质探究实验题、定量测定实验题等。
②考查的角度有仪器的识别与应用、物质的制备、除杂与分离、物质的性质探究与验证、实验现象的分析与描述、实验结论的评价与计算等,常以实验流程图的题干形式给出信息。



2019年新课标全国卷(1、2、3卷)理科数学备考宝典3.程序框图一、2018年考试大纲 二、新课标全国卷命题分析 三、典型高考试题讲评2011—2018年新课标全国(1卷、2卷、3卷)理科数学分类汇编——3.程序框图 一、考试大纲1.算法的含义、程序框图(1)了解算法的含义,了解算法的思想.(2)理解程序框图的三种基本逻辑结构:顺序、条件分支、循环.2.基本算法语句理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含 义.二、新课标全国卷命题分析程序框图一般考含有循环体的较多,都比较简单,一般与数列求和联系较多,难度不大.程序框图考查考生的读图能力,这是数学阅读能力的一个重要方面,主要考查方向有:对程序框图基本知识的考查、程序框图与函数、数列知识相结合,考查分段函数、条件分支结构,强化基础知识及其应用。
三、典型高考试题讲评 题型1 算法的基本结构例1(2017·新课标Ⅱ,理8)执行右面的程序框图,如果输入的1a =-,则输出的S =( )A .2B .3C .4D .5 【答案】B 解析:∵ 00S =,01K =,01a =-,S S a K =+⋅,a a =-,∴ 执行第一次循环:11S =-﹑11a =﹑12K =;执行第二次循环:21S =﹑21a =-﹑23K =;执行第三次循环:32S =-﹑31a =﹑34K =;执行第四次循环:42S =﹑41a =-﹑45K =;执行第五次循环:53S =-﹑51a =﹑ 56K =;执行第五次循环:63S =﹑61a =﹑67K =;当676K =>时,终止循环,输出63S =,故输出值为3.题型2 完善程序框图例2(2017·新课标Ⅰ,8)右面程序框图是为了求出满足321000n n ->的最小偶数n 两个空白框中,可以分别填入( )A .A >1000和n =n +1B .A >1000和n =n +2C .A ≤1000和n =n +1D .A ≤1000和n =n +2 解析:因为要求A 大于1000时输出,且框图中在“否”时输出∴“”中不能输入A 1000>,排除A 、B , 又要求n 为偶数,且n 初始值为0,“”中n 依次加2可保证其为偶,故选D ;题型3 算法案例例3 (2015新课标2理8)下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入,a b 分别为14,18,则输出的a =( )A.0B. 2C. 4D. 14 解析:本题就是将古代数学中的“更相减损术”用程序框图来展现,根据程序框图可知, 在执行程序过程中,a ,b 的值依次为14a =,18b =;4b =;10a =;6a =;2a =;2b =,到此有2a b ==,程序运行结束,输出a 的值为2.故选B .2011年—2018年新课标全国卷理科数学试题分类汇编3.程序框图(2018·新课标Ⅱ,7)为计算11111123499100S =-+-+⋅⋅⋅+-,设计了右侧的程序框图, 则在空白框中应填入( )A .1i i =+B .2i i =+C .3i i =+D .4i i =+ (2017·新课标Ⅰ,8)右面程序框图是为了求出满足321000n n ->的最小偶数n ,那么在和两个空白框中,可以分别填入( )A .A >1000和n =n +1B .A >1000和n =n +2C .A ≤1000和n =n +1D .A ≤1000和n =n +2(2017·新课标Ⅱ,8)执行右面的程序框图,如果输入的1a =-,则输出的S =( )A .2B .3C .4D .5 (2017·新课标Ⅰ,8) (2017·新课标Ⅱ,8) (2017·新课标Ⅲ,7)(2017·新课标Ⅲ,7).执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A .5B .4C .3D .2(2016·新课标Ⅰ,9)执行右面的程序框图,如果输入的0=x ,1=y ,1=n ,则输出y x ,的值满足( )A .x y 2=B .x y 3=C .x y 4=D .x y 5=(2016·新课标Ⅰ,9) (2016··新课标Ⅱ,8) (2016·新课标Ⅲ,7)(2016··新课标Ⅱ,8)中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的x =2,n =2,依次输入的a 为2,2,5,则输出的s =( ) A .7B .12C .17D .34(2016·新课标Ⅲ,7)执行右面的程序框图,如果输入的a =4,b =6,那么输出的n =A. 3B. 4C. 5D. 6(2015·新课标Ⅰ,9)执行右面的程序框图,如果输入的0.01t =,则输出的n =( )A .5B .6C .7D .8(2015·新课标Ⅰ,9) (2015··新课标Ⅱ,8) (2014··新课标Ⅱ,7)(2015··新课标Ⅱ,8)右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”. 执行该程序框图,若输入a ,b 分别为14,18,则输出的a =( ) A .0B .2C .4D .14(2014·新课标Ⅰ,7)执行下图的程序框图,若输入的,,a b k 分别为1,2,3,则输出的M =( )A .203 B .165 C .72 D .158(2014··新课标Ⅱ,7)执行右面程序框图,如果输入的x ,t 均为2,则输出的S = ( )A .4B .5C .6D .7(2013·新课标Ⅰ,5)执行下面的程序框图,如果输入的t ∈[-1,3],则输出的s 属于( ).A .[-3,4]B .[-5,2]C .[-4,3]D .[-2,5](2013··新课标Ⅱ,6)执行右面的程序框图,如果输入的10N =,那么输出的S =( )A .11112310++++ B .11112!3!10!++++ C .11112311++++D .11112!3!11!++++(2012·新课标Ⅰ,6)如果执行右边和程序框图,输入正整数N (2N ≥)和 实数1a ,2a ,…,N a ,输出A ,B ,则( ) A .A B +为1a ,2a ,…,N a 的和B .2A B+为1a ,2a ,…,N a 的算术平均数 C .A 和B 分别是1a ,2a ,…,N a 中最大的数和最小的数 D .A 和B 分别是1a ,2a ,…,N a 中最小的数和最大的数(2013·新课标Ⅰ,5) (2013··新课标Ⅱ,6) (2012·新课标Ⅰ,6)(2012··新课标Ⅱ,6)如果执行右边的程序框图,输入正整数N (N ≥2)和实数a 1, a 2,…,a N ,输入A 、B ,则( )A. A +B 为a 1, a 2,…,a N 的和B.2B A +为a 1, a 2,…,a N 的算术平均数C. A 和B 分别是a 1, a 2,…,a N 中最大的数和最小的数D. A 和B 分别是a 1, a 2,…,a N 中最小的数和最大的数(2012··新课标Ⅱ,6) (2011·新课标Ⅰ,3) (2011··新课标Ⅱ,3) (2011·新课标Ⅰ,3)执行右面的程序框图,如果输入的N 是6,那么输出的p 是 A .120 B .720 C .1440 D .5040(2011··新课标Ⅱ,3)执行右面的程序框图,如果输入的N 是6,那么输出的p 是( )A .120B .720C .1440D .50402011年—2018年新课标全国卷理科数学试题分类汇编3.程序框图(解析版)(2018·新课标Ⅱ,7)为计算11111123499100S =-+-+⋅⋅⋅+-,设计了右侧的程序框图, 则在空白框中应填入( )A .1i i =+B .2i i =+C .3i i =+D .4i i =+ 【答案】B 解析:从N 、T 和式结构上看,属于累和结构,奇数项的和与偶数项的和,从以上的结构与分析我们知道偶数或奇数的间隔为2,即2i i =+ (2017·新课标Ⅰ,8)右面程序框图是为了求出满足321000n n ->的最小偶数n ,那么在和两个空白框中,可以分别填入( )A .A >1000和n =n +1B .A >1000和n =n +2C .A ≤1000和n =n +1D .A ≤1000和n =n +2 否是开始 k<N输出p输入N 结束k =1, p =1 k =k+1p=p·k【答案】D 解析:因为要求A 大于1000时输出,且框图中在“否”时输出∴“”中不能输入A 1000>,排除A 、B ,又要求n 为偶数,且n 初始值为0,“”中n 依次加2可保证其为偶,故选D ;(2017·新课标Ⅱ,8)执行右面的程序框图,如果输入的1a =-,则输出的S =( )A .2B .3C .4D .5 【答案】B 解析:【解析】解法一:常规解法∵ 00S =,01K =,01a =-,S S a K =+⋅,a a =-,∴ 执行第一次循环:11S =-﹑11a =﹑ 12K =;执行第二次循环:21S =﹑21a =-﹑23K =;执行第三次循环:32S =-﹑31a =﹑ 34K =;执行第四次循环:42S =﹑41a =-﹑45K =;执行第五次循环:53S =-﹑51a =﹑56K =;执行第五次循环:63S =﹑61a =﹑67K =;当676K =>时,终止循环,输出63S =,故输出值为3.解法二:数列法()11nn n S S n -=+-⋅,1n K n =+,裂项相消可得()121nin i S S i =-=-⋅∑;执行第一次循环:11S =-﹑11a =﹑12K =,当6n K >时,6n =即可终止,61234564S +=-+-+=,即63S =,故输出值为3.(2017·新课标Ⅲ,7).执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( ).A .5B .4C .3D .2【答案】D 解析: 程序运行过程如下表所示:初始状态 0 100 1 第1次循环结束 100 2 第2次循环结束9013此时9091S =<首次满足条件,程序需在3t =时跳出循环,即2N =为满足条件的最小值.故选D.(2016·新课标Ⅰ,9)执行右面的程序框图,如果输入的0=x ,1=y ,1=n ,则输出y x ,的值满足A .x y 2=B .x y 3=C .x y 4=D .x y 5=【答案】C 解析:第一次循环:220,1,136x y x y ==+=<;第二次循环:22117,2,3624x y x y ==+=<; ny y n x x =-+=,21ny x ,,输入开始y x ,输出1+=n n ?3622≥+y x 是否第三次循环:223,6,362x y x y ==+>; 输出32x =,6y =,满足4y x =;故选C . (2016··新课标Ⅱ,8)中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的x =2,n =2,依次输入的a 为2,2,5,则输出的s =( ) A .7B .12C .17D .34【答案】C 解析:第一次运算:0222s =⨯+=,第二次运算:2226s =⨯+=,第三次运算:62517s =⨯+=,故选C .(2016·新课标Ⅲ,7)执行右面的程序框图,如果输入的a =4,b =6,那么输出的n =A. 3B. 4C. 5D. 6 【答案】B 解析:列表如下 4 2 6-2 42 6-2 46 46460 6 10 16 201234 【考点】程序框图(2015·新课标Ⅰ,9)执行右面的程序框图,如果输入的0.01t =,则输出的n =( )A .5B .6C .7D .8 解析:0.01t =保持不变,初始值11,0,0.52s n m ====, 执行第1次,0.5,0.25,1s m n ===,s t >,执行循环体; 执行第2次,0.25,0.125,2s m n ===,s t >,执行循环体; 执行第3次,0.125,0.0625,3s m n ===,s t >,执行循环体; 执行第4次,0.0625,0.03125,4s m n ===,s t >,执行循环体;执行第5次,0.03125,0.015625,4s m n ===,s t >,执行循环体;执行第6次,0.015625,0.0078125,5s m n ===,s t >,执行循环体;执行第7次,0.0078125,0.00390625,6s m n ===,s t <,跳出循环体,输出7n =,故选C ..(2015··新课标Ⅱ,8)右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”. 执行该程序框图,若输入a ,b 分别为14,18,则输出的a =( ) A .0B .2C .4D .14【答案】B 解析:程序在执行过程中,a ,b 的值依次为a =14,b =18,b =4,a =10,a =6,a =2,b =2,此时a =b =2程序结束,输出a 的值为2,故选B .(2014·新课标Ⅰ,7)执行下图的程序框图,若输入的,,a b k 分别为1,2,3,则输出的M =( )A .203 B .165 C .72 D .158【答案】D 解析:输入1,2,3a b k ===;1n =时:1331,2,222M a b =+===; 2n =时:28382,,3323M a b =+===;3n =时:3315815,,28838M a b =+===;4n =时:输出158M = .(2014··新课标Ⅱ,7)执行右面程序框图,如果输入的x ,t 均为2,则输出的S = ( )A .4B .5C .6D .7【答案】D 解析::输入的x ,t 均为2.判断12≤?是,1221M =⋅=,235S =+=,112k =+=;判断22≤?是,2222M =⋅=,257S =+=,213k =+=,判断32≤?否,输出7S =. (2013·新课标Ⅰ,5)执行下面的程序框图,如果输入的t ∈[-1,3],则输出的s 属于( ).A .[-3,4]B .[-5,2]C .[-4,3]D .[-2,5] 【答案】A 解析:. 若t ∈[-1,1),则执行s =3t ,故s ∈[-3,3).若t ∈[1,3],则执行s =4t -t 2,其对称轴为t =2.故当t =2时,s 取得最大值4.当t =1或3时,s 取得最小值3,则s ∈[3,4]. 综上可知,输出的s ∈[-3,4].(2013··新课标Ⅱ,6)执行右面的程序框图,如果输入的10N =,那么输出的S =( )A .11112310++++ B .11112!3!10!++++ C .11112311++++D .11112!3!11!++++【答案】B 解析::由程序框图知,当k =1,S =0,T =1时,T =1,S =1; 当k =2时,12T =,1=1+2S ; 当k =3时,123T =⨯,111+223S =+⨯;当k =4时,1234T =⨯⨯,1111+223234S =++⨯⨯⨯; … … … … ; 当k =10时,123410T =⨯⨯⨯⨯,1111+2!3!10!S =+++, k 增加1变为11,满足k >N ,输出S ,故选B .(2012·新课标Ⅰ,6)如果执行右边和程序框图,输入正整数N (2N ≥)和 实数1a ,2a ,…,N a ,输出A ,B ,则( )A .AB +为1a ,2a ,…,N a 的和B .2A B+为1a ,2a ,…,N a 的算术平均数C .A 和B 分别是1a ,2a ,…,N a 中最大的数和最小的数D .A 和B 分别是1a ,2a ,…,N a 中最小的数和最大的数【答案】C 解析:由程序框图可知,A 表示1a ,2a ,…,N a 中最大的数,B 表示1a ,2a ,…,N a 中最小的数,故选择C .(2012··新课标Ⅱ,6)如果执行右边的程序框图,输入正整数N (N ≥2)和实数a 1, a 2,…,a N ,输入A 、B ,则( )A. A +B 为a 1, a 2,…,a N 的和B.2B A +为a 1, a 2,…,a N 的算术平均数C. A 和B 分别是a 1, a 2,…,a N 中最大的数和最小的数D. A 和B 分别是a 1, a 2,…,a N 中最小的数和最大的数【答案】C 解析:由程序框图判断x >A 得A 应为a 1,a 2,…,a N 中最大的数,由x <B 得B 应为a 1,a 2…,a N 中最小的数.(2011·新课标Ⅰ,3)执行右面的程序框图,如果输入的N 是6,那么输出的p 是A .120B .720C .1440D .5040【答案】B 解析:解析:框图表示1n n a n a -=⋅,且11a =所求6a =720 选B(2011··新课标Ⅱ,3)执行右面的程序框图,如果输入的N 是6,那么输出的否是是1k k =+B x=A x =结束输出A ,B?k N ≥?x B <kx a =?x A >开始输入N ,1a ,2a ,…,N a1k =,1A a =,1B a = 否是 否p 是( )A .120B .720C .1440D .5040【答案】B 解析:框图表示1n n a n a -=⋅,且11a =所求6a =720,故选B.否是开始 k<N输出p 输入N 结束k =1, p =1 k =k+1p=p·k。