应用数学与计算综合测验一

-平均数= (5+8+12+14+21+24+30+33) / 8
-中位数=中间两个数（12和14）的平均数= (12+14) / 2
-众数=出现次数最多的数，此数据组中没有重复的数，因此无众数
2.设小华年龄为x，小李年龄为y。
-根据题意：x = 2y
- 5年后：x + 5 = 1.5(y + 5)
-示例：案例分析题要求学生分析学生计算错误的原因，并提出教学策略。
8. **应用题：**考察学生对数学知识在实际情境中的应用能力。
-示例：应用题第1题考察了学生对统计知识的理解和应用。
9. **思考题：**考察学生对教育理论和实践的综合思考能力。
-示例：思考题要求学生结合新课程改革背景，探讨如何整合学科教学。
1. **小学教育的本质和任务**：
-考点：小学教育的基本特点、任务和目标。
-难点：理解新课程改革背景下小学教育的核心理念和实施策略。
2. **小学语文教学**：
-考点：阅读能力、写作能力和表达能力的培养。
-难点：如何通过多样化的教学方法激发学生的想象力和创造力。
3. **小学数学教学**：
-考点：数学基础知识的掌握，如数与代数、几何、统计与概率等。
-解方程组得：x = 10, y = 5
-因此，现在小华10岁，小李5岁。
####思考题（共10分）
在新课程改革背景下，有效整合学科教学，促进学生的全面发展，可以从以下几个方面进行：
**教学目标：**
-制定跨学科的教学目标，强调知识的应用和综合能力的培养。
**教学内容：**
-设计跨学科的项目或主题，如“环境保护”涉及科学、语文、社会等学科。

四年级数学下册四则运算与简便计算练习题（1）四则运算与简便计算练习题课堂讲解(前三页)⼀、填空1．在⼀个算式⾥，如果只有加减法，要（）计算，如果只有乘除法，要（）计算。

2．在⼀个算式⾥，如果含有加、减、乘、除四种运算，要先算（），再算（）。

3．在⼀个算式⾥如果含有⼩括号，要先算（）。

⼆、⼝算36 ÷ 3 100 － 62 24 － 8 ＋ 10 75 ×30 371 － 3715 ＋ 24 － 12 200 ÷ 40 84 ÷ 4 48 ÷ 8 × 993÷100= 159+61= 600÷20= 78+222= 405-60= 1000÷8=17×11= 7600÷400= 480÷120= 695-75= 25×17×4=225-99= 640÷40= 468+199= 620-340= 3200÷80=三、⽐⼀⽐，算⼀算49 ＋ 17 － 25 240 ÷ 40 × 5 300 － 50 × 249 －（17 ＋ 25）240 ＋ 40 × 5 300 － 50 × 20 × 0四、把下⾯⼏个分步式改写成综合算式．（1）960÷15=64 64-28=36 综合算式___________________.（2）75×24=1800 9000-1800=7200 综合算式___________ ______（3）810-19=791 791×2=1582 1582+216=1798 综合算式_____________（4）96×5=480 480+20=500 500÷4=125 综合算式_____________五、计算下⾯各题121 － 111 ÷ 37 （121 － 111 ÷ 37）× 5 280 ＋ 650 ÷ 1345 × 20 × 3 1000 －（280 ＋ 650 ÷ 13）（95 － 19 × 5 ）÷74 （120 － 103）× 50 760 ÷ 10 ÷ 38 （270 ＋ 180）÷（30 －15）707 － 35 × 20 （95 －19 × 5 ）÷7419×96-962÷74 10000-(59＋66)×64 5940÷45×(798-616)（270 ＋ 180）÷（30 － 15）(315×40-364)÷7 12520÷8×(121÷11)(2010-906)×(65+15) 707 －35 × 2050＋160÷40（58+370）÷（64-45） 120-144÷18+35 347+45×2-4160÷52 （58+37）÷（64-9×5）95÷（64-45） 178-145÷5×6+42420+580-64×21÷28 812-700÷（9+31×11）（136+64）×（65-345÷23）85+14×（14+208÷26）121 －111 ÷ 37（120 － 103）× 50（284+16）×（512-8208÷18） 120-36×4÷18+35（58+37）÷（64-9×5）45 × 20 × 3（121 －111 ÷ 37）× 5 280 ＋ 650 ÷ 131000 －（280 ＋650 ÷ 13）760 ÷ 10 ÷ 389846－87×(360÷60) 508×345÷(1526－1521)（124－85）×12÷26 （59＋21）×（96÷8）325÷13×(266-250) 140-90÷5+678六、⾯各题，怎样简便就怎样计算。

小学四年级数学下册应用题300题四年级下学期应用题（一）1.某化肥厂一月份生产化肥310吨，二月份生产400吨，三月份生产490吨化肥，平均每月生产化肥多少吨？2.一匹马每天吃12千克草,照这样计算, 25匹马,一星期可吃多少千克草?(用两种方法计算)3.工人XXX和徒弟做机器零件,XXX每小时做45个,徒弟每小时做28个,XXX工作6小时,徒弟工作8小时,他们共做多少个机器零件?4.工厂有煤8000千克,原计划烧25天,由于改进炉灶,实际烧了32天,平均每天比原计划节约多少千克?5.工地需要1280袋水泥,用8辆大车4次才全部运来,一辆大车,一次可运多少袋化肥?(用两种方法计算)6.农具厂上半年生产农具4650件，下半年生产农具5382件，全年平均每月生产多少件？7.服装加工部用120米布可做成人制服24套,如果做儿童服装,可做30套,每套儿童服装比成人服装少用布多少米?8.一个养鸡场四月份卖出只鸡,五月份卖出的比四月份的2倍还少200只,两个月一共卖出多少只鸡?9.某工厂原计划一年生产农具4800部,实际用10个月就完成了任务,实际平均每月比原计划每月多生产多少部农具?研究参考10.一台机器8小时可以加工320个零件,照如许计算,要用5台机器加工2000个零件,需要几何小时?11.某煤矿四月份计划出煤吨,技术革新后平均每天比原计划每天增产256吨,四月份实际生产多少吨煤?(按30天计算)12.第一小组有6个人,其中5个人语文考试的平均分是85分,加上XXX的分数后,平均成绩是87分,XXX的考试成绩是多少分?13.两个水管同时向池中放水,粗管每小时放水15吨,细管每小时放水11吨,经过8小时把水放满,这个水池能装多少吨水?(用两种不同方法计算)14.一个长方形操场,长50米,宽40米,扩建后长和宽分别增加5米,扩建后操场面积增加了多少平方米?15.一个长方形长21厘米,是宽的3倍,求这个长方形的周长和面积各是几何?16.一吨废纸可以生产纸张700千克,假如一千克纸能制成25本练本,那末12吨废纸生产的纸张能制成几何本练本?17.录制一份气功报告需要4盒录音带,录满一面录音带需要30分,这份报告一共录了多少小时?18.一台推土机3小时可铺路600米,假如每小时多铺20米,8小时能铺几何米?研究参考19.李庄农民往粮库运小麦,第一天运了10车,第二天运了7车,每车运小麦2吨400千克,两天共运多少千克?合多少吨多少千克?20. 100块湿砖重450千克,每块砖吹干后减轻850克, 100块湿砖在吹干后重多少千克?21.一台自动包装机用20秒包装135块糖,照这样计算,这个机器1小时能包装多少块糖?22.一根钢管长9米，用去了3.6米，剩下的比用去的长几何米？23.某造纸厂七月份造纸1.56吨，八月份造纸1.68吨，九月份造纸数比七、八月份的和少0.74吨，九月份造纸多少吨？24.工厂食堂上半年烧煤30吨，下半年比上半年节约了2.45吨，下半年烧煤多少吨？25.一双布鞋7.8元，一双球鞋9.5元，一双球鞋比一双布鞋贵多少元？26.有两个粮仓，第一个粮仓里有粮食56.5吨，比第二个粮仓少9吨，两个粮仓共有粮食多少吨？27.甲乙两队合铺一条长94.6千米的公路，甲队铺了32.5千米，乙队铺了29.5千米，还剩几何千米没有铺？进修参考28.一个等腰三角形周长1米，腰长是0.4米，这个三角形底边长多少米？29．一台磨面机每小时磨面800千克，照这样计算，6台磨面机5小时能磨面粉多少千克？(用两种方法解答)30．一堆煤共800吨，用5辆卡车，16次可以运完，平均每辆卡车每次运几吨？31．一辆汽车6小时行了300千米，一列火车6小时行了600千米，火车比汽车每小时多行多少千米？33．XXX气象小组一周中，测得每天的最高气温分别为：31、31、34、32、33、30、33度．这一周最高平均气温是多少度？34．XXX步行4千米680米，用了1时18分，平均每分行多少米？35．一辆自重3吨的卡车，车上装有7000千克木料，要通过一座限重11吨的桥．算一算，卡车能否通过这座桥？36．28行播种机的宽度是4米．用拖拉机牵引，每小时行5千米，可以播种多少公顷土地？37．甲、乙两堆货物共重8000千克，已知甲堆货物的重量是乙堆货物的4倍．求甲、乙两堆货物各重几何千克？38．一列火车上午6小时行了366千米，下午4小时行了276千米．下午比上午平均每小时多行几何千米？进修参考39．一个工厂前6个月用煤120吨，后半年用煤102吨．每吨煤按80元计算，后半年比前半年平均每月用煤节约多少元？40．一个林场前年植树1480棵，去年植树的棵数是前年的2倍，本年植树比前两年植树的总数还多420棵，本年植树几何棵？41．100千克稻谷可碾米75千克，1千克稻谷可碾米几何千克？42．1千克黄豆可出油0.38千克，100千克黄豆可出油多少千克？1000千克黄豆呢？43．XXX用43.20元买了10支钢笔，每支钢笔几何元？买100支如许的钢笔应付几何元？44．甲数是3.8，乙数是38，在它们的末尾都添上两个零，这时乙数是甲数的多少倍？45．黉舍买足球和篮球共用65.76元，已知买足球用了42.86元，买篮球用了几何钱？46．同学们采集树种子，一班采集了32.56千克，二班采集了38.45千克，两个班共采集多少千克？47．XXX买数学参考书用了24.28元，买语文参考书用了23.76元，他付给售货员50元，应找回几何钱？进修参考48．工人叔叔修路，第一天修了18.65米，第二天比第一天多修了5.6米，两天共修多少米？50．同学们去春游．每辆汽车运了48人，用3辆汽车运了2趟才把所有师生送去．春游的师生共有多少人？51.装订车间每人每小时装订课本640册，照这样计算，12人8小时装订课本多少册？52.汽车队开展节约用油活动，12辆车一年共节约汽油7200千克，平均每辆车每个月节约汽油几何千克？53.一部电话机售价320元，一台“彩电”的售价是电话机售价的8倍，一台电脑的售价比“彩电”售价的3倍还多1000元，一台电脑几何元？54.两个车间生产零件，5天后甲车间生产1520个零件，乙车间生产1280个零件，若每天工作8小时，乙车间比甲车间每小时少生产多少个零件？55．据统计篮鲸3小时能游108米，海豚5小时能游245米，每小时篮鲸比海豚少游多少米？56．一个生产小组有25人，一天加工零件1500个，后来又调入了8个人，照这样计算，生产小组每天比原来多加工多少个零件？57．XXX一天卖出“南极人”纯棉内衣90套，上午卖出38套，每套纯棉内衣218元，上午比下午少卖出几何元？进修参考XXX用2台磨面机5天磨面粉千克，每天工作8小时．第一台每小时磨面314千克，第二台每小时磨面多少千克？59．XXX读一本书，第一天读10页，以后每天都比前一天多读5页，最后一天读40页正好读完．他一共读了多少天？60.一本书，XXX看了45页，没看的比看了的3倍少8页，这本书共有多少页？61.师徒二人共同加工一批零件，师傅每小时加工125个，徒弟每小时加工100个，8小时完成任务，完成任务时，师傅比徒弟共多加工多少个零件？师傅和徒弟共加工多少个零件？62.已知甲、乙、丙三个数的平均数是268，丁数为148，求这四个数的平均数是几何？63.同学们参加环保活动，六一班42人，平均每人清理环境80平方米，六二班38人，共清理环境2800平方米，两个班平均每人清理环境多少平方米？64.XXX骑车行20千米400米，用了1时20分．平均每小时骑车行多少千米多少米？65.工厂运来一批原料，已经运来15吨400千克，剩下的比运来的3倍多500千克．这批原料共有多少千克？合多少吨多少千克？66.打字员每分钟打150个字，要打一份字的书稿需要几小时几分钟？研究参考67.一块长方形稻田，宽200米，长是宽的2倍，这块稻田有多少公顷？如果每公顷稻田收稻谷6500千克，这块地共收稻谷多少千克？68．10吨小麦可磨面粉8.5吨，100千克小麦可磨面粉多少吨？69．100吨海水含盐3吨，10吨海水含盐多少吨？70．XXX共生产铁钉3000千克，装进100只木箱后，还剩500千克，还需要几何只木箱？71．一袋米吃去32.18千克，还有17.82千克，这袋米原有多少千克？72．一个足球48.36元，一个篮球54.27元，XXX用150元买足球，篮球各一个，应找回多少元？73．一个长方形的长是0.54米，比宽多8厘米，这个长方形的周长是多少米？74．两根电线，第一根长48.3米，比第二根长6.5米，第一根用去9.4米后，比第二根少多少米？75．一把椅子35.4元，比一张桌子便宜16.2元，学校买了100套桌椅，共用多少元？76．一根绳子分成三段，第一、二段长38.7米，第二、三段长41.6米，第一、三段长39.7米．求三段绳子各长多少米？77．甲仓有粮58.4吨，乙仓有粮44吨，从甲仓运走几何吨粮以后，乙仓存粮是甲仓的2倍？78．学校买来320套课桌椅，每张桌子55元，每把椅子36元，学校共花多少元？(用两种方法解答)79．7名工人8天加工服装2632件，照这样计算，再增加3名工人，1天能加工服装多少件？80．果园里有梨树132棵，比桃树少44棵，苹果树的棵数等于梨树、桃树总棵数的2倍，果园里有苹果树多少棵？81．学校为同学们买排球花了360元，买足球花的钱比买排球的2倍少60元，又恰好是买篮球的2倍，学校买篮球比买排球少花了多少元？XXX把清扫一块长39米，宽20米的绿地任务分配给两个班，甲班有40人，乙班有38人，如果按人数分配，每班应清扫多少平方米？83．三筐苹果共重110.5千克，如果从第一筐取出18.6千克，从第二筐取出23.5千克，从第三筐取出20.4千克，则三筐所剩的苹果重量相同，原来三筐苹果各有多少千克？84．公园里有松树64棵，比柳树少16棵，杨树的棵数即是松树、柳树棵数和的3倍，公园里有杨树几何棵？85．儿童节时两组同学用3小时共做花240朵，第一组每小时做44朵花，第二组有6人，平均每人每小时做花几何朵？86．民工队修一条水渠，计划天天修84米，34天可以完成，结果天天修102米，可以提早几天完成？87．一块长方形菜地面积是1公顷，长125米．一块麦田长250米，这两块地的宽相等，麦田的面积是多少平方米？合多少公顷？88．一辆汽车从甲地开往乙地，前两小时行了90千米，第三小时行了48千米，正好抵达乙地．这辆汽车平均每小时行几何千米？89．果园收一批苹果．用小筐装每筐能装25千克，需要28个筐，假如改用10个大筐装，还要剩下50千克．平均每个大筐装几何千克？90．甲、乙两个班都有学生48人，每人做16朵纸花送给幼儿园，一共送了多少朵？91．甲、乙两地相距456千米，一列火车从甲地开往乙地，平均每小时行76千米，需要几小时？92．有两个粮食堆栈，假如第一个堆栈运走2500千克，两个堆栈存粮一样多，已知第二个堆栈存粮原有千克，原来两个粮库共存粮几何千克？93．师傅每小时生产机器零件64个，徒弟每小时生产48个零件，师傅3小时生产的零件，徒弟要几小时完成？94．一块长方形菜地长120米，宽60米，如果每12平方分米种一棵西红柿，这块菜地一共可以种多少棵西红柿？如果每棵西红柿收3千克，一共收西红柿多少千克？95．甲有14.8元，乙有15.2元，俩人要合买一个足球，一个足球的价钱是他俩人钱数总和的2倍，一个足球多少元，他们还差多少元？96．一台机器3小时耕地15公顷，照如许计算，要耕75公顷地，用5台机器需要几何小时？97．商店有14箱鸭蛋，卖出去250千克后，还剩4箱零20千克，每箱鸭蛋有几何千克？98．XXX为山区同学捐书，四年级捐240本，五年级捐的是四年级的2倍，六年级比五年级多捐120本，平均每个年级捐几何本？99．粮店运进大米、面粉各20袋，每袋大米90千克，每袋面粉25千克，运进的大米比面粉多多少千克？(用两种方法解答)研究参考100．两根绳共长48.4米，从第一根上剪去6.4米后，第二根比第一根剩下的2倍还多6米．两根绳原来各长几何米？101.4、五年级的学生采集树种，四年级采集树种18．6千克，四年级比五年级少采集2.5千克，两个年级一共采集几何千克树种？102.一个车间原来每月用电2450千瓦·时，开展节约活动后，原来一年的用电量，现在可多用2个月，这个车间平均每月节约用电几何千瓦·时？103．新修一条公路，已经完成64千米，剩下的比完成的3倍少25千米，这条公路全长多少千米？104．化肥厂六月份生产化肥483.6吨，七月份上半月生产254.8吨，下半月生产287.4吨，七月份比六月份多生产化肥多少吨？105．师傅每天加工200个零件，徒弟5天的工作量等于师傅4天的工作量．徒弟单独工作要多少天才能完成1120个零件？106．要架一条7200米长的电缆，计划12天完成任务，实际9天就完成任务，实际每天比计划每天多架设多少米？107．一双布鞋25.65元，一双皮鞋比布鞋贵216.45元，XXX 买一双皮鞋付给售货员300元，应找回多少元钱？108．果园里种苹果树2600棵，桃树1150棵，梨树1250棵．平均每棵树占地14平方米，这个果园占地多少公顷？109.同学们参加植树劳动，四年级共有96人，每人栽3棵树，五年级有87人，每人栽4棵树，五年级比四年级多栽树多少棵？110.第一小组6个同学数学测验的成绩分别是：86、79、98、100、89、94，算一算他们的平均分是几何？111.一辆汽车3小时行了135千米，一架飞机飞行的速度是汽车的28倍还少60千米，这架飞机每小时行几何千米？112.一个服装厂5天生产洋装850套，照如许计算，一个月生产洋装几何套？(一个月按30天计算)113.商店运来8筐苹果和12筐梨，每筐苹果38千克，每筐梨42千克，商店共运来水果几何千克？114.某工地需水泥240吨，用5辆汽车来运，每辆汽车每次运3吨，需运多少次才能运完？(用两种综合式解答)115.甲乙两地相距750千米，一辆汽车以每小时50千米的速度行驶，多少小时可以到达乙地？(列出含有未知数的等式再解) 116.XXX、XXX，共有12支铅笔，XXX和XXX共有20支铅笔，他们平均每人有多少支铅笔？117．某小学三年级和四年级要给620棵树浇水，三年级天天浇40棵，浇了8天；剩下的由四年级来浇，5天浇完，平均天天浇几何棵？118．3台织布机4小时织布336米，照这样计算，1台织布机8小时织布多少米？119．甲乙两地相距560千米，一辆汽车从甲地开往乙地，每小时行48千米，另一辆汽车从乙地开往甲地，每小时行32千米．两车从两地相对开出5小时后，两车相距多少千米？120．一段公路原计划20天修完．实际天天比原计划多修45米，提早5天完成义务．原计划天天修路几何米？100．两根绳共长48.4米，从第一根上剪去6.4米后，第二根比第一根剩下的2倍还多6米．两根绳原来各长几何米？101.4、五年级的学生采集树种，四年级采集树种18．6千克，四年级比五年级少采集2.5千克，两个年级一共采集几何千克树种？四年级数学下册应用题练题（二）1、一个滴水的水龙头一星期要白白流掉84千克水。

以下是一些行测题库中的数学运算题目：
有 3 个箱子，每个箱子中都装有 5 个球，其中 1 个箱子中装的是红球，1 个箱子中装的是绿球，1 个箱子中装的是红球和绿球，且 3 个箱子中球的颜色均不相同。

如果从 3 个箱子中分别摸出 1 个球，那么摸出的 3 个球中至少有 1 个红球的概率是多少？
甲、乙两人同时从 A 地出发前往 B 地，甲的速度为9 千米/小时，乙的速度为 6 千米/小时。

当甲到达 B 地后立即返回 A 地，在距离 B 地12 千米处与乙相遇。

那么A、B 两地之间的距离是多少千米？
某班级共有40 名学生，一次考试后，数学老师统计了所有学生的成绩，并计算出班级的平均分为85 分。

其中男生的平均分为88 分，女生的平均分为82 分。

问这个班级男生比女生多多少人？
这些题目旨在测试考生的数学运算能力，包括概率、行程问题和平均数等。

你可以使用适当的数学方法和公式来解决这些问题。

如果你需要更多的数学运算题目或详细的解答，请告诉我你的具体需求，我将尽力提供帮助。

小学五年级数学 （上）应用题
1、工程队修一条8.5千米的公路，开始平均每天修0.65千米， 修了5天后，剩下的路要7天修完，平均每天要修多少千米？ 2、工程队修一条8.5千米的公路，开始平均每天修0.65千 米，为了加快进度，以后平均每天多修0.1千米，剩下的路 还要修多少天？ 3、工程队修一条7.8千米的公路，原计划每天修0.65千米， 实际每天比计划多修0.13千米，这样可以比计划提前几天完 成？ 4、工程队修一条路，原计划每天修0.65千米，12天完成， 实际每天多修0.13千米，实际多少天完成？（实际提前几天 完成？） 5、工程队原计划用12天修一段7.8千米的公路，实际每 天多修0.13千米，实际多少天完成？（实际提前几天完成？） 6、工程队修一条路，原计划每天修0.65千米，12天完成， 实际每天修的是计划的1.2倍，实际多少天完成？（实际提 前几天完成？）
1．甲有14.8元，乙有15.2元，俩人要合买一个足球，一个足球的价钱是 他俩人钱数总和的2倍，一个足球多少元，他们还差多少元？ 2．一台机器3小时耕地15公顷，照这样计算，要耕75公顷地，用5台机 器需要多少小时？ 3．商店有14箱鸭蛋，卖出去250千克后，还剩4箱零20千克，每箱鸭蛋 有多少千克？ 4．光明小学为山区同学捐书，四年级捐240本，五年级捐的是 四年级的 2倍，六年级比五年级多捐120本，平均每个年级捐多少本？ 5．粮店运进大米、面粉各20袋，每袋大米90千克，每袋面粉25千克， 运进的大米比面粉多多少千克？(用两种方法解答) 6．两根绳共长48.4米，从第一根上剪去6.4米后，第二根比第一根剩下 的2倍还多6米．两根绳原来各长多少米？
7. 四、五年级的学生采集树种，四年级采集树种18．6千克，四年级比 五年级少采集2.5千克，两个年级一共采集多少千克树种？ 8. 一个车间原来每月用电2450千瓦•时，开展节约活动后，原来一年的 用电量，现在可多用2个月，这个车间平均每月节约用电多少千瓦•时？ 9. 同学们参加植树劳动，四年级共有96人，每人栽3棵树，五年级有87 人，每人栽4棵树，五年级比四年级多栽树多少棵？ 10. 第一小组6个同学数学测验的成绩分别是：86、79、98、100、89、 94，算一算他们的平均分是多少？ 11. 一辆汽车3小时行了135千米，一架飞机飞行的速度是汽车的28倍还 少60千米，这架飞机每小时行多少千米？ 12. 一个服装厂5天生产西服850套，照这样计算，一个月生产西服多少 套？(一个月按30

六年级上册数学应用题综合练习（一）1、小明5投3中，小强6投4中。

他们两人的命中率分别是多少？2、六年级有学生160人，已达到国家体育标准的有120人。

达标率是多少？3、六一班有45人，上学期跳远测验有80%的人及格。

及格的同学有多少人？4、2000kg 花生仁能榨出花生油760kg ，花生的出油率是多少？5、油菜的出油率是42%。

2100kg 油菜籽可榨油多少千克？6、某校有480人，只有5%的学生没有参加保险。

没有参加保险的学生有多少人？7、油菜的出油率是42%。

一个榨油厂榨出2100kg 菜籽油，用了多少千克油菜籽？8、小飞家原来每月用水10吨，更换了节水龙头后每月用水9吨，每月用水比原来节约了百分之几？9、学校图书室原有图书1400册，今年图书册数增加了12%。

现在图书室有多少册图书？10、王伯家菜地共800平方米，准备用52种西红柿，剩下的按2：1的面积比种黄瓜和茄子。

三种蔬菜的面积分别是多少平方米?11、要搅拌20吨混凝土，水泥、沙子和石子的比是2：3：5。

需要水泥、沙子和石子各多少吨？12、用120cm 的铁丝做一个长方体框架，长、宽、高的比是3：2：1。

这个长方体的长、宽、高分别是多少？13、小明的体重是35kg ，他的体重比爸爸的体重轻158，小明爸爸的体重是多少千克？14、有一组互相咬合的齿轮 ⑴大齿轮有140个齿，小齿轮的齿数是大齿轮的51。

小齿轮有多少个齿？⑵小齿轮有28个齿，是大齿轮的51。

大齿轮有多少个齿？⑶小齿轮每分钟转400周，大齿轮每分钟转的周数比小齿轮少54。

大齿轮每分钟转多少周？⑷大齿轮每钟转80周，比小齿轮每分钟转的周数少54。

小齿轮每分钟转多少周？15、某电视机厂去年全年生产电视机108万台，其中上半年产量是下半年的54。

这个电视机厂上半年和下半年的产量分别是多少万台？16、一套运动服裤子价钱比上衣少60元，裤子价钱是上衣的32。

上衣和裤子分别是多少钱？17、冰融化成水后，水的体积是冰的体积的1110。

四年级数学上册常考应用题姓名：___________ 班级：____________ 成绩：_________1、一辆旅游车在平原和山区各行了2小时，最后到达山顶。

已知旅游车在平原每小时行50千米，山区每小时行30千米。

这段路程有多长？2、东关小学体育队有71人，其中15人是篮球队员，田径队员的人数是篮球队员的2.4倍，其余的是足球队员。

足球队有多少人？3、商店运来16筐苹果，每筐42.5千克。

运来的梨比苹果重量的2倍少120千克。

运来的梨有多少千克？4、一个学生的家离学校有3千米。

他每天早晨骑车上学，以每小时15千米的速度行进，恰好准时到校。

一天早晨，由于逆风，开始的1千米，他只能够以每小时10千米的速度骑行。

剩下的路程他应以什么速度骑行，才能够准时到校？5、河堤的一边栽了75棵柳树。

每两棵柳树中间栽一棵桃树，栽桃树多少棵？6、陈老师去体育用品店买了12个篮球，每个篮球的价钱是63元，又买了8个排球用去240元。

陈老师一共用了多少元钱？7、松柏林能分泌杀菌素，可以净化空气。

如果1公顷松柏林每天分泌杀菌素54千克，24公顷松柏林31天分泌杀菌素多少千克？8、东东看一本150页的故事书，第一天看了40页，第二天看的与第一天同样多，还有多少页没有看？9、有一列数：2，5，8，11，14……根据上面的规律，你知道第1995个数是多少吗？10、王大伯第一天收获30筐土豆，共重750千克，第二天比第一天多收获10筐。

照这样计算，第二天收获多少千克？两天一共收获多少千克？11、工程队计划修一条长5000米的路，原计划每天修200米，实际上只用了20天就完成了任务。

实际上每天比原计划多修多少米？12、电冰箱厂原计划每天生产50台电冰箱可以在预定的时间里完成。

实际每天生产60台，结果提前3天完成了任务。

这批电冰箱共有多少台？13、一箱水果糖重25千克，多少箱水果糖重750千克？14、飞机场上有72架飞机，平均分成4个队，每个队分成3个组，每组有多少架飞机？15、水果店运来香蕉625千克，橘子480千克。

一、加减法中的速算与巧算速算巧算的核心思想和本质：凑整。

常用的思想方法总结如下：（1）分组凑整法．把几个互为“补数”的减数先加起来，再从被减数中减去，或先减去那些与被减数有相同尾数的减数．“补数”就是两个数相加，如果恰好凑成整十、整百、整千……，就把其中的一个数叫做另一个数的“补数”．（2）加补凑整法．有些算式中直接凑整不明显，这时可“借数”或“拆数”凑整．（3）数值原理法．先把加在一起为整十、整百、整千……的数相加，然后再与其它的数相加．（4）“基准数”法，基准当几个数比较接近于某一整数的数相加时，选这个整数为“基准数”（要注意把多加的数减去，把少加的数加上）二、乘法凑整思想核心：先把能凑成整十、整百、整千的几个乘数结合在一起，最后再与前面的数相乘，使得运算简便。

例如：425100⨯=，81251000⨯=⨯=，520100⨯=（去8数，重点记忆）123456799111111111⨯⨯=（三个常用质数的乘积，重点记忆）711131001理论依据：乘法交换率：a×b=b×a乘法结合率：(a×b) ×c=a×(b×c)乘法分配率：(a+b) ×c=a×c+b×c积不变规律：a×b=(a×c) ×(b÷c)=(a÷c) ×(b×c)三、乘、除法混合运算的性质（1）商不变性质：被除数和除数乘（或除）以同一个非零数，其商不变．即：()()()()0a b a n b n a m b m m÷=⨯÷⨯=÷÷÷≠，0n≠（2）在连除时，可以交换除数的位置，商不变．即：a b c a c b÷÷=÷÷（3）在乘、除混合运算中，被乘数、乘数或除数可以连同运算符号一起交换位置（即带着符号搬家）．例如：a b c a c b b c a⨯÷=÷⨯=÷⨯（4）在乘、除混合运算中，去掉或添加括号的规则去括号情形：①括号前是“×”时，去括号后，括号内的乘、除符号不变．即()()a b c a b c a b c a b c⨯⨯=⨯⨯⨯÷=⨯÷②括号前是“÷”时，去括号后，括号内的“×”变为“÷”，“÷”变为“×”．即()()a b c a b c a b c a b c÷⨯=÷÷÷÷=÷⨯添加括号情形：加括号时，括号前是“×”时，原符号不变；括号前是“÷”时，原符号“×”变为“÷”，“÷”变为“×”．即()()()() a b c a b c a b c a b c a b c a b c a b c a b c⨯⨯=⨯⨯⨯÷=⨯÷÷÷=÷⨯÷⨯=÷÷（5）两个数之积除以两个数之积，可以分别相除后再相乘．即()()()()()()a b c d a c b d a d b c⨯÷⨯=÷⨯÷=÷⨯÷上面的三个性质都可以推广到多个数的情形．一、加减速算【例 1】计算：（1）117＋229＋333＋471＋528＋622（2）（1350＋249＋468）＋（251＋332＋1650）（3）756－248－352（4）894－89－111－95－105－94【考点】分组凑整【难度】☆【题型】解答【解析】在这个例题中，主要让学生掌握加、减法分组凑整的方法。

数 学 练 习（一）〔有理数加减法运算练习〕一、加减法法则、运算律的复习。

A ．△同号两数相加，取__________________,并把____________________________。

1、（–3）+（–9）2、85+（+15）3、（–361）+（–332） 4、（–3.5）+（–532）△绝对值不相等的异号两数相加，取_________________________,并用____________________ _____________. 互为__________________的两个数相加得0。

1、(–45) +（+23）2、（–1.35）+6.353、412+（–2.25） 4、（–9）+7△ 一个数同0相加，仍得_____________。

1、（–9）+ 0=______________;2、0 +（+15）=_____________。

B ．加法交换律：a + b = ___________ 加法结合律：(a + b) + c = _______________1、（–1.76）+（–19.15）+ (–8.24)2、23+（–17）+（+7）+（–13）3、（+ 341）+（–253）+ 543+（–852） 4、52+112+（–52）C ．有理数的减法可以转化为_____来进行，转化的“桥梁”是___________。

△减法法则：减去一个数，等于_____________________________。

即a –b = a + ( )1、（–3）–（–5）2、341–（–143） 3、0–（–7）D ．加减混合运算可以统一为_______运算。

即a + b –c = a + b + _____________。

1、（–3）–（+5）+（–4）–（–10）2、341–（+5）–（–143）+（–5）△把–2.4–（–3.5）+（–4.6）+ (+3.5)写成省略加号的和的形式是______________，读作:__________________________，也可以读作：__________________________。

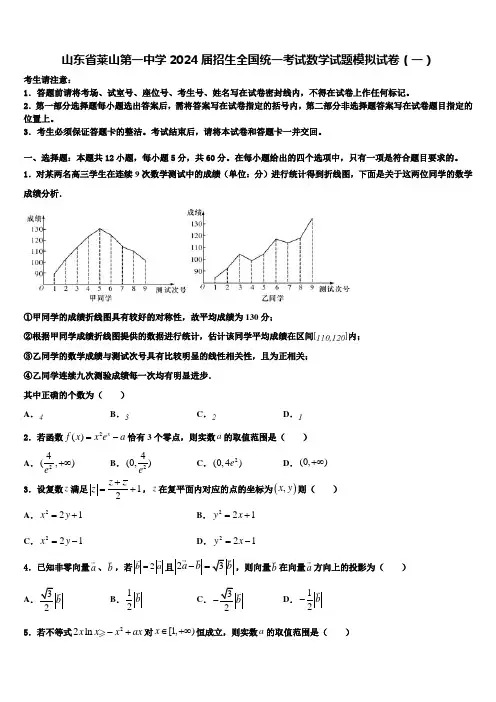
山东省莱山第一中学2024届招生全国统一考试数学试题模拟试卷（一）考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．对某两名高三学生在连续9次数学测试中的成绩（单位：分）进行统计得到折线图，下面是关于这两位同学的数学成绩分析．①甲同学的成绩折线图具有较好的对称性，故平均成绩为130分； ②根据甲同学成绩折线图提供的数据进行统计，估计该同学平均成绩在区间内；③乙同学的数学成绩与测试次号具有比较明显的线性相关性，且为正相关； ④乙同学连续九次测验成绩每一次均有明显进步． 其中正确的个数为（ ） A ．B ．C ．D ．2．若函数2()xf x x e a =-恰有3个零点，则实数a 的取值范围是（ ） A ．24(,)e+∞ B ．24(0,)eC ．2(0,4)eD ．(0,)+∞3．设复数z 满足12z zz +=+，z 在复平面内对应的点的坐标为(),x y 则（ ） A ．221x y =+ B ．221y x =+ C ．221x y =-D ．221y x =-4．已知非零向量a 、b ，若2b a =且23a b b -=，则向量b 在向量a 方向上的投影为（ ） A 32b B ．12b C ．32b D ．12b -5．若不等式22ln x x x ax -+对[1,)x ∈+∞恒成立，则实数a 的取值范围是（ ）A ．(,0)-∞B ．(,1]-∞C ．(0,)+∞D ．[1,)+∞6．如图所示，已知双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F ，双曲线C 的右支上一点A ，它关于原点O 的对称点为B ，满足120AFB ∠=︒，且||2||BF AF =，则双曲线C 的离心率是（ ）.A ．33B ．72C 3D 77．有一圆柱状有盖铁皮桶（铁皮厚度忽略不计），底面直径为20cm ，高度为100cm ，现往里面装直径为10cm 的球，在能盖住盖子的情况下，最多能装（ ） 235 2.236≈≈≈） A ．22个B ．24个C ．26个D ．28个8．设复数z 满足21z i z -=+，z 在复平面内对应的点为(,)x y ，则（ ） A ．2430x y --= B ．2430x y +-=C ．4230x y +-=D ．2430x y -+=9．在满足04i i x y <<≤，i i y xi i x y =的实数对(),i i x y (1,2,,,)i n =⋅⋅⋅⋅⋅⋅中，使得1213n n x x x x -++⋅⋅⋅+<成立的正整数n 的最大值为( ) A ．5B ．6C ．7D ．910．已知双曲线22221(0)x y a b a b-=>>的右焦点为F ，过F 的直线l 交双曲线的渐近线于A B 、两点，且直线l 的倾斜角是渐近线OA 倾斜角的2倍，若2AF FB =，则该双曲线的离心率为（ ） A ．324B ．33C ．305D ．5211．已知i 为虚数单位，实数,x y 满足(2)x i i y i +=-，则||x yi -= ( ) A ．1B 2C 3D 512．已知某几何体的三视图如图所示，则该几何体的体积是（ ）A ．643B ．64C ．323D ．32二、填空题：本题共4小题，每小题5分，共20分。

小学四年级数学上册应用题姓名：___________ 班级：____________ 成绩：_________1、一个林场用喷雾器给树喷药，2台喷雾器4小时喷了200棵。

照这样计算，5台喷雾器6小时可以喷多少棵？2、东关小学体育队有71人，其中15人是篮球队员，田径队员的人数是篮球队员的2.4倍，其余的是足球队员。

足球队有多少人？3、母亲比儿子大32岁，3年后母亲的年龄是儿子的5倍，儿子今天几岁？4、甲乙丙三个数的平均数是36，乙丙两数的平均数是28，那么甲数是多少？5、学校校礼堂每排有28个座位，四年级共有180人，可以坐满几排？还剩几人？6、学校准备发练习本，发给15个班，每班144本，救灾需要留40本作为备用。

学校应买多少本练习本？7、王村准备在长200米，宽150米的长方形稻田里施化肥，按每公顷施化肥238千克，共需施化肥多少千克？8、等腰直角三角形两条相邻的边分别是8米、5米，它的周长是多少米？9、一个学生的家离学校有3千米。

他每天早晨骑车上学，以每小时15千米的速度行进，恰好准时到校。

一天早晨，由于逆风，开始的1千米，他只能够以每小时10千米的速度骑行。

剩下的路程他应以什么速度骑行，才能够准时到校？10、小明看一本180页的故事书，已经看了3天，平均每天看24页。

剩下的平均每天看36页，还要几天才能看完？11、包装一个小礼盒需要31厘米长的彩带，现有320个这样的小礼盒，估一估，准备90米的彩带够吗？12、修路工人用25天修了950米。

照这样计算，剩下的760米，还需要多少天可以修完？13、文文家新房子装修，打算给长方形的客厅铺上木地板，客厅长7.5米，宽4.6米，家居市场给出的木地板的价格是每平方米120元。

他家客厅木地板大约需要多少钱？14、一棵树苗16元，买3棵送1棵。

一次买3棵，每棵便宜多少钱？15、某小学少先队员进行队列表演。

每列25人，可以排成12列。

如果每列减少10人，可以排成多少列？16、饲养组养了20只黑猫，养的花猫比黑猫的3倍还多5只，养的花猫比黑猫多多少只？17、阳光幼儿园共有学生495人，全部更换了新的单人课桌和椅子。

小学六年级数学应用题大全一.解答题(共50题，共271分)1.一桶汽油，第一次用去总数的30%，第二次用去总数的，还剩50L，这桶汽油原来有多少升？2.汕尾和广州两地相距约330千米，一辆汽车从汕尾出发开往广州，已经行驶了全程的，还要行驶多少千米才能到达广州？3.六年级男生有180人，女生有160人，男生比女生多百分之几？女生比男生少百分之几？4.一桶洗衣粉，第一次倒出全桶的22%，第二次倒出全桶的23%，还剩下2.2千克，这桶洗衣粉原有多少千克？5.一个直径为8米的圆形花坛，要在花坛外围修一条1米宽的石头小路。

（1）石头小路的面积是多少？（2）如果每平方米需要花费100元，修这条石头小路总共要花费多少钱？6.一根长15.7米的铁丝正好在一个圆形线圈上绕了10圈，这个圆形线圈的直径是多少厘米？7.画一个直径是12厘米的圆，并在圆中画一个圆心角是100°的扇形。

求这个扇形的面积。

8.家乐福连锁店2018年11月份的营业额是42万元，比10月份增加了5万元。

11月份营业额比10月份增加了百分之几？9.儿童玩具厂生产了800个玩具，其中5个不合格，这批玩具的合格率是多少?10.西乡今年荔枝大丰收，产量达到3.6万吨，比去年增产了20%，西乡去年荔枝的产量多少万吨?11.商店促销，一个电饭煲现价220元，比原价降价15%，这个电饭煲原价多少元？12.水果店购进桃子120千克，比葡萄的75%还少30千克。

水果店购进葡萄多少千克？13.一个圆形洞口，直径为1m，一个身高1.45m的小男孩不能直身钻进去，如果这个洞口的周长增加1.57m，小男孩能直身钻进去吗？（填能或不能）14.无脊椎动物中游泳速度最快的是乌贼，它的最高速度每分约是km，海豚的速度是乌贼的，海豚每分约能游多远？15.一个水杯按36元出售，则亏了25%，这个水杯的进价是多少？（列方程解答）16.一个绿化队修理草坪，用去了900元钱，比原来节省了300元钱，求节省了百分几?17.根据不同的条件列式，不计算。

2024年广东省汕头市潮阳实验学校中考数学一模试卷一、选择题：本题共10小题，每小题3分，共30分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.与为倒数的数为( )A. B. C. 5 D.2.下列计算正确的是( )A. B. C. D.3.有一组数据：2，，2，4，6，7这组数据的中位数为( )A. 2B. 3C. 4D. 64.如图，，，，则的度数为( )A.B.C.D. 755.下列说法正确的个数是( )①的立方根是；②如果一个角的两边分别平行于另一个角的两边，则两个角一定相等；③正三角形既是中心对称又是轴对称图形；④顺次连接对角线相等的四边形四边中点所得的四边形必是矩形；⑤三角形的内心到三角形的三个顶点的距离相等A. 0个B. 1个C. 2个D. 3个6.如图，在中，，分别以点A、B为圆心，以适当的长为半径作弧，两弧分别交于E，F，作直线EF，D为BC的中点，M为直线EF上任意一点.若，面积为10，则长度的最小值为( )A.B. 3D. 57.已知二次函数的解析式是，结合图象回答：当时，函数值y的取值范围是( )A.B.C.D.8.将反比例函数的图象绕坐标原点O逆时针旋转，得到如图的新曲线，与过点，的直线相交于点C、D，则的面积为( )A. 8B. 3C.D.9.对于实数a，b，定义运算“*”如下：，例如：，则方程的根的情况是( )A. 没有实数根B. 只有一个实数根C. 有两个相等的实数根D. 有两个不相等的实数根10.如图，正方形纸片ABCD，P为正方形AD边上的一点不与点A，点D重合将正方形纸片折叠，使点B落在点P处，点C落在点G处，PG交DC于点H，折痕为EF，连接BP，BH，BH交EF于点M，连接下列结论：①；②；③PB平分；④；⑤，其中正确结论的个数是( )B. 4C. 3D. 2二、填空题：本题共5小题，每小题3分，共15分。

11.分解因式：______.12.某商场的打折活动规定：凡在本商场购物，可转动转盘一次，并根据所转结果付账.其中不打折的概率为______.13.某楼梯的侧面如图所示，测得，，则该楼梯的高度______.14.如图，一艘轮船以20海里/小时速度从南向北航行，当航行至A处时，测得小岛C在轮船的北偏东45度的方向处，航行一段时间后到达B处，此时测得小岛C在轮船的南偏东60度的方向处．若海里，则轮船航行的时间为______.15.如图，已知一次函数的图象与坐标轴分别交于点A，B两点，的半径为1，P是线段AB上的一个点，过点P作的切线PQ，切点为Q，则PQ的最小值为______.三、计算题：本大题共1小题，共6分。

最新小学五年级数学应用题大全(上.下册)小学五年级上学期数学应用题精选一.行程问题：1.火车从甲城到乙城.现已行了200千米.是剩下路程的4倍。

甲乙两城相距多少千米？2.甲港到乙港的航程有210千米.一艘轮船运货从甲港到乙港.用了6小时.返回时每小时比去时多行7千米.返回时用了几小时？3.小方从家到学校.每分钟走60米.要14分钟.如果她每分钟多走10米.需要多少分钟？4.一辆汽车3小时行了135千米.一架飞机飞行的速度是汽车的28倍还少60千米.这架飞机每小时行多少千米？5.某工地需水泥240吨.用5辆汽车来运.每辆汽车每次运3吨.需运多少次才能运完？6.甲乙两地相距750千米.一辆汽车以每小时50千米的速度行驶.多少小时可以到达乙地？7.甲乙两地相距560千米.一辆汽车从甲地开往乙地.每小时行48千米.另一辆汽车从乙地开往甲地.每小时行32千米．两车从两地相对开出5小时后.两车相距多少千米？8.一段公路原计划20天修完．实际每天比原计划多修45米.提前5天完成任务．原计划每天修路多少米？9.这辆汽车每秒行18米,车的长度是18米,隧道长324米,这辆汽车全部通过隧道要用多长时间10.石家庄到承德的公路长是546千米.红红一家从石家庄开车到承德游览避暑山庄,如果平均每小时行驶78千米,上午8时出发,那么几时可以到达二.面积问题：1.一个平行四边形四条边长度相等都是5厘米高是3厘米求这个平行四边形面积是多少？2. 一个长方形长是18厘米宽是长的一半多2厘米求这个长方形面积和周长分别是多少？3.一个正方形边长9厘米把它分成四个相等大小的小正方形请问小正方形的面积是多少？4.一个长方形是由两个大小相等的正方形拼成的正方形的边长是4厘米求这个长方形的面积是多少？5.一个正方形纸条周长是64厘米把这个正方形对折变成两个大小相同的长方形求这两个大小相同的长方形的面积是多少？三.综合问题：1.商店运来梨子650千克.运来的苹果是梨子的2倍。

小学四年级上册数学应用题【100道】应用题是指将所学知识应用到实际生活实践的题目。

小编整理了小学四年级上册数学应用题【100道】，希望对你有帮助! 小学四年级上册数学应用题50道1、一只山雀5天大约能吃800只害虫，照这样计算，一只山雀一个月大约能吃多少只害虫？（一个月按30天计算。

）2、一辆长客车3小时行了174千米，照这样的速度，它12小时可以行多少千米？3、张爷爷买3只小羊用了75元，他还想再买5只这样的小羊，需要准备多少钱？4、5箱蜜蜂一年可以酿375千克蜂蜜。

小林家养了这样的蜜蜂12箱，一年可以酿多少千克蜂蜜？5、育英小学的180名少先队员在"爱心日"帮助军属做好事。

这些少先队员平均分成5队，每队分成4组活动，平均每组有多少名少先队员？6、刘叔叔带700元买化肥，买了16袋化肥，剩60元。

每袋化肥的价钱是多少？7、春芽鸡场星期一收的鸡蛋，18千克装一箱。

装好8箱后还剩16千克。

星期一收了多少千克鸡蛋？8、王叔叔从县城开车去王庄送化肥。

去的时候每小时行40千米，用了6小时，返回时只用千米，用了了5小时。

返回时平均每小时行多少千米？9、一辆旅游车在平原和山区各行了2小时，最后到达山顶。

已知旅游车在平原每小时行50千米，山区每小时行30千米。

这段路程有多长？10、公路两边植树，每边每千米要植树25棵，这条路长120千米，一共植树多少棵？11、学校准备发练习本，发给15个班，每班144本，还要留40本作为备用。

学校应买多少练习本？12、一棵树苗16元，买3棵送1棵。

一次买3棵，每棵便宜多少钱？13、洗发水每瓶15元，商场开展促销活动，买4瓶送1瓶。

一次买4瓶，每瓶便宜多少元？14、一只熊猫一天要吃15千克饲料，动物园准备24袋饲料，每袋20千克，这些饲料够一只熊猫吃30天吗？15、汽车从甲地到乙地送货，去时用了6小时，速度是32千米/小时，回来只用了4小时，回来的速度是多少？16、小明上山用了4小时，每小时行3千米，下山的速度加快，是6千米/时，下山用了多长的时间？17、车间原计划每天生产15台机器，24天就可以完成，实际每天生产18台，实际只要几天就可以完成任务？18、实验小学要为三、四年级的学生每人买一本价格为12元的作文辅导书。

一,列式计算1.20除200与124的和,再加上42,和是多少2.78减去17加上101,再乘以2,积是多少3.23个915除以5的商,比4500少多少4.36乘以18的积再减去36所得的差,除以18, 商是多少5.18乘36的积,减去18除36的商,差是多少6.27乘以4的积,加上54乘以5的积,和是多少7.72与28的和,乘以它们的差,积是多少8. 45减去15的差,除以32与29的差,商是多少9.30加上96减去12与5的积所得的差,和是多少10.470减去32于14的积,再加上129;和是多少11.761减去103的5倍,所得的差再除以3,商是多少12.104除以8的商比58乘以12的积少多少13.36与18减去36除以18所得的差相乘,积是多少应用题1、装订车间每人每小时装订课本640册,照这样计算,12人8小时装订多少册2、汽车队开展节约用油活动,12辆车一年共节约汽油7200千克,平均每辆车每个月节约汽油多少千克3、一部电话机售价320元,一台“彩电”的售价是电话机售价的8倍,一台电脑的售价比“彩电”售价的3倍还多1000元,一台电脑多少元4、两个车间生产零件,5天后甲车间生产1520个零件,乙车间生产1280个零件,若每天工作8小时,乙车间比甲车间每小时少生产多少个零件5、一本书,小华看了45页,没看的比看了的3倍少8页,这本书共有多少页6、师徒二人共同加工一批零件,师傅每小时加工125个,徒弟每小时加工100个,8小时完成任务,完成任务时,师傅比徒弟共多加工多少个零件师傅和徒弟共加工多少个零件7、甲、乙、丙三个数的平均数是268,丁数为148,这四个数的平均数是多少8、同学们参加环保活动,六一班42人,平均每人清理环境80平方米,六二班38人,共清理环境2800平方米,两个班平均每人清理环境多少平方米9、小华骑车行20千米400米,用了1时20分．平均每小时骑车行多少多少米10、工厂运来一批原料,已经运来15吨400千克,剩下的比运来的3倍多500千克．这批原料共有多少千克合多少吨多少千克11、打字员每分钟打150个字,要打一份30000字的书稿需要几小时几分钟12、一块长方形稻田,宽200米,长是宽的2倍,这块稻田有多少公顷如果每公顷稻田收稻谷6500千克,这块地共收稻谷多少千克13．10吨小麦可磨面粉8.5吨,100千克小麦可磨面粉多少吨14．100吨海水含盐3吨,10吨海水含盐多少吨15．五金厂共生产铁钉3000千克,装进100只木箱后,还剩500千克,还需要多少只木箱16．学校买来320套课桌椅,每张桌子55元,每把椅子36元,学校共花多少元用两种方法解答17．7名工人8天加工服装2632件,照这样计算,再增加3名工人,1天能加工服装多少件18．果园里有梨树132棵,比桃树少44棵,苹果树的棵数等于梨树、桃树总棵数的2倍,果园里有苹果树多少棵19．学校为同学们买排球花了360元,买足球花的钱比买排球的2倍少60元,又恰好是买篮球的2倍,学校买篮球比买排球少花了多少元20．学校把清扫一块长39米,宽20米的绿地任务分配给两个班,甲班有40人,乙班有38人,如果按人数分配,每班应清扫多少平方米21．三筐苹果共重110.5千克,如果从第一筐取出18.6千克,从第二筐取出23.5千克,从第三筐取出20.4千克,则三筐所剩的苹果重量相同,原来三筐苹果各有多少千克22．篮鲸3小时能游108米,海豚5小时能游245米,每小时篮鲸比海豚少游多少米23．一个生产小组有25人,一天加工零件1500个,后来又调入了8个人,照这样计算,生产小组每天比原来多加工多少个零件24．华联商厦一天卖出“南极人”纯棉内衣90套,上午卖出38套,每套纯棉内衣218元,上午比下午少卖出多少元25．粮食加工厂用2台磨面机5天磨面粉28800千克,每天工作8小时．第一台每小时磨面314千克,第二台每小时磨面多少千克26．小刚读一本书,第一天读10页,以后每天都比前一天多读5页,最后一天读40页正好读完．他一共读了多少天27．一袋米吃去32.18千克,还有17.82千克,这袋米原有多少千克28．一个足球48.36元,一个篮球54.27元,王老师用150元买足球,篮球各一个,应找回多少元29．一个长方形的长是0.54米,比宽多8厘米,这个长方形的周长是多少米30．两根电线,第一根长48.3米,比第二根长6.5米,第一根用去9.4米后,比第二根少多少米31．一把椅子35.4元,比一张桌子便宜16.2元,学校买了100套桌椅,共用多少元32．一根绳子分成三段,第一、二段长38.7米,第二、三段长41.6米,第一、三段长39.7米．求三段绳子各长多少米33．甲仓有粮58.4吨,乙仓有粮44吨,从甲仓运走多少吨粮以后,乙仓存粮是甲仓的2倍34. 一个修路队三天共修路6.5千米;已知第一天修了1.94千米,第二天比第一天多修0.58千米;第三天修了多少千米35. 某工厂积极开展植树活动;第一车间45人共植树315棵；第二车间42人,平均每人植树8棵;第一车间比第二车间少植树多少棵36. 商店运来梨子650千克,运来的苹果是梨子的2倍;这两种水果共运来多少千克画图表示出题里的已知条件和问题,再解答37. 某校办工厂去年原计划平均每月生产文具盒3190个,实际生产11个月就完成了全年的计划任务;实际比原计划平均每月多生产多少个文具盒38. 甲乙两地相距750千米,一辆汽车以每小时50千米的速度行驶,多少小时可以到达乙地列出含有未知数的等式再解39. 小华、小林,共有12支铅笔,小刚和小红共有20支铅笔,他们平均每人有多少支铅笔40. 一个服装厂5天生产西服850套,照这样计算,一个月生产西服多少套一个月按30天计算41. 商店运来8筐苹果和12筐梨,每筐苹果38千克,每筐梨42千克,商店共运来水果多少千克42. 某工地需水泥240吨,用5辆汽车来运,每辆汽车每次运3吨,需运多少次才能运完用两种综合式解答43. 同学们参加植树劳动,四年级共有96人,每人栽3棵树,五年级有87人,每人栽4棵树,五年级比四年级多栽树多少棵44. 第一小组6个同学数学测验的成绩分别是：86、79、98、100、89、94,算一算他们的平均分是多少45. 一辆汽车3小时行了135千米,一架飞机飞行的速度是汽车的28倍还少60千米,这架飞机每小时行多少千米46. 四、五年级的学生采集树种,四年级采集树种18．6千克,四年级比五年级少采集2.5千克,两个年级一共采集多少千克树种47. 车间原来每月用电2450千瓦·时,开展节约活动后,原来一年的用电量,现在可多用2个月,这个车间平均每月节约用电多少千瓦·时48. 一辆小汽车2小时行180千米,照这样的速度,6小时行几千米49. 一块边长20米的麦地共收小麦240千克,平均每平方米收小麦几千克50. 某厂有男工45人,女工比男工的4倍少10人;这个厂有多少工人51. 容器里正好装满10千克纯酒精,倒出5.6千克后用水加满;这时水比纯酒精多多少52. 制衣厂有8000件衣服要包装,每箱装衣服24件;这些衣服最多能装多少箱,还剩多少件53. 四年级一班有6个小组,每组7个同学;平均每人采集5只昆虫制作标本;全班同学一共采集了多少只昆虫54. 六年级学生参加植树活动;一班有40人,平均每人植树4棵,二班有38人,平均每人植树5棵,二班比一班多植树多少棵55. 文具店去年平均每月营业额9000元,今年预计能提前2个月达到去年的营业额今年预计平均每月的营业额是多少元56. 给1100名学生每人配一个水杯,每个水杯3元;“六一”期间超市推出优惠价,每买10个送1个;学校在优惠期购买,比平时便宜多少钱57. 甲有14.8元,乙有15.2元,俩人要合买一个足球,一个足球的价钱是他俩人钱数总和的2倍,一个足球多少元,他们还差多少元58．一台机器3小时耕地15公顷,照这样计算,要耕75公顷地,用5台机器需要多少小时59．商店有14箱鸭蛋,卖出去250千克后,还剩4箱零20千克,每箱鸭蛋有多少千克60．光明小学为山区同学捐书,四年级捐240本,五年级捐的是四年级的2倍,六年级比五年级多捐120本,平均每个年级捐多少本61．粮店运进大米、面粉各20袋,每袋大米90千克,每袋面粉25千克,运进的大米比面粉多多少千克用两种方法解答62．两根绳共长48.4米,从第一根上剪去6.4米后,第二根比第一根剩下的2倍还多6米．两根绳原来各长多少米63、某小学三年级和四年级要给620棵树浇水,三年级每天浇40棵,浇了8天；剩下的由四年级来浇,5天浇完,平均每天浇多少棵64．3台织布机4小时织布336米,照这样计算,1台织布机8小时织布多少米65．甲乙两地相距560千米,一辆汽车从甲地开往乙地,每小时行48千米,另一辆汽车从乙地开往甲地,每小时行32千米．两车从两地相对开出5小时后,两车相距多少千米66．一段公路原计划20天修完．实际每天比原计划多修45米,提前5天完成任务．原计划每天修路多少米67．新修一条公路,已经完成64千米,剩下的比完成的3倍少25千米,这条公路全长多少千米68．化肥厂六月份生产化肥483.6吨,七月份上半月生产254.8吨,下半月生产287.4吨,七月份比六月份多生产化肥多少吨69．师傅每天加工200个零件,徒弟5天的工作量等于师傅4天的工作量．徒弟单独工作要多少天才能完成1120个零件70．要架一条7200米长的电缆,计划12天完成任务,实际9天就完成任务,实际每天比计划每天多架设多少米71．一双布鞋25.65元,一双皮鞋比布鞋贵216.45元,王老师买一双皮鞋付给售货员300元,应找回多少元钱72．果园里种苹果树2600棵,桃树1150棵,梨树1250棵．平均每棵树占地14平方米,这个果园占地多少公顷73. 8名工人7天共加工服装2632件,平均每名工人每天加工服装多少件74. 学校里有松树38棵,柳树比松树多23棵,杨树的棵数等于松树和柳树总棵数的2倍;有多少棵杨树75. 育苗小学五年1班有6个组每组8人;全班同学帮助学校搬运红砖1728块,平均每人搬运红砖多少块76、修一条铁路,已经修好824米,剩下的一段比修好的2倍少36千米,这条铁路长多少千米77、在第二十届奥运会上,中国队获得15枚金牌,比第二十四届奥运会上中国队获得的金牌数多10枚,第二十五届奥运会上,中国队获得的金牌数比二十四的3倍多1枚,中国队在第二十五届奥运会上获得枚金牌78、少先队员帮助收柿子,第一小队收86,实第二小队的2倍,得比第二小队得3倍少16.5筐, 第三小队收多少筐79、甲乙两列火车同时从两地相对开出.甲每小时行80千米, 乙每小时行90千米,5小时后两车相遇,甲乙两地相距多少千米80、甲乙两地相距416千米,小龙和小明分别从两地相对走来,小龙每分走50米,小明每分走54米,几分钟后相遇81、王师傅和徒弟同时合作1200个零件,经过8小时完成.王师傅每小时做91个 .徒弟每小时做多少个82、甲乙两列火车分别从两站同时相对开出,甲车每小时行45.6千米;乙车每小时行54.4千米,5小时候两车相遇,两站相距多少千米83、甲乙两列火车分别从两站同时相对开出,甲车每小时行45.6千米;乙车每小时比甲车多行7.8千米,3小时候两车相遇, 两站相距多少千米提问:能不能直接用公式做为什么84、两队筑路工人和修一条路,七天修完,甲队每天修50米,乙队2天修120米,这条路长多少米85、志明和小龙同时从两地对面走来,4分后两人距离100米,志明每分走54米,小龙每分走50米,两地相距多少米86、两个工程队修一条长4000米的路.一队从西往东每天修96米,两队共同修了15天,还有多少米路没有修87、小青和小芳同时从相距700米的两地相对走来,小青每分走60米,小芳每分走80米,几分后两人相遇88、两个城市相距246千米,两辆汽车自两地同时相对开出,甲车每小时行40千米,乙车每小时行的比甲车多2千米,开出几小时后两车相遇89、师徒二人共同生产432个机器零件,徒弟每小时生产18个零件,师傅每小时生产的是徒弟的2倍,他们几小时才能完成任务完成任务时各生产了多少个90、装满一个水池需要60吨水,甲水管单独开5小时可装满,乙水管每小时可放入18吨水,如果两个水管同时开,几小时可以把这个水池装满91、洪波电视机厂要装配2650台电视机,一个组每天装配50台,另一个组每天装配48台,两各组同时装配,还差200台完成任务.两组已经装配了多少天92、两列火车从相距420千米的两个车站相对开出,3小时相遇.一列火车的时速是69千米,另一列火车的时速是多少千米93、电视机厂计划月产按30天计算电视机1200台,由两组同时组装.结果比计划多组装60台,第一组每天组装21台,第二组每天组装多少台94、甲乙两艘轮船从相距1010千米的两地同时相对出发,8小时后还相距514千米,已知甲船每小时航行28千米, 乙船每小时航行多少米95、从甲城到乙城的铁路长738千米,两列火车从两城同时相对开出.甲城开出的火车平均每小时行59千米, 乙城开出的火车平均每小时行64千米,两列火车几小时相遇相遇时各行了多少千米96、甲乙两人合作600个零件,甲每小时做46个,乙每小时做54个,几小时做完做完时,甲比乙少做多少个97、两个修路队四天和修公路400米,,一队平均每天修54米,二队平均每天修多少米一队每天比二队多修多少米98、刚和小明家相距1200米,小钢住学校的西侧,小明住学校的东侧,两人同时向学校走去,经过8分同时到达学校,小刚每分行70米,小明每分行多少米他们两家各距学校多少米99、小青和小芳同时从相距740米的两地相对走来,小青每分走60米,小芳每分走80米,4分钟后二人还相距多少米剩下的路由小青一人走,还需几分钟和小芳相遇100、一部书稿共有144000个字,甲打字员单独打要90小时完成, 乙打字员单独打要72小时完成乙两个打字员单独打,平均每个小时各打多少字如果两人和打,几小时可以打完这部书稿101、甲车床3小时可制作18个机器零件, 乙车床2小时可制作16个机器零件, 两个车床一小时共制作多少个零件两个车床要共同制作84个零件,需要几小时102、甲乙两列火车同时从相距660千米的两个城市对开,甲每小时行85千米乙每小时行80千米,相遇时乙车行了多少千米问：能不能直接用公式做要求相遇时乙车行了多少千米,必须先求什么103、学校离县城26千米,甲乙二人分别从两地相向行走,甲每小时走4千米,乙每小时走5千米,甲从县城出发8千米后,乙才走.乙出发几小时后二人相遇104、个小组组装一批自行车,甲组每天组装92辆, 乙组每天组装98辆,甲组先组装了460辆后,两组又一起工作8天才完成任务,这批自行车共多少辆问:这批自行车包括几部分谁已知必须先求谁105、甲乙两个港口相距264千米,拖船顺水每小时航行11千米, 逆水每小时航行11千米,在甲乙两港之间往返一次需要多少时间因为顺水和逆水时的速度不同,所以必须分别求往返时间,再求和. 106、北京到天津的铁路大约长138千米,一列火车从北京开到天津,休息2小时后又返回北京,共用了6小时,这列火车平均每小时行多少千米因为往返的时间是6-2=4时,必须找和它对应的往返的路程.138×2 138×2÷6-2或根据单程138千米,去找和它对应的单程时间6-2÷2138÷6-2÷2107、一台锅炉平均每月用煤4000千克,一个居民小区新增加5台锅炉,一年要用煤多少千克108、汽车配件小组有20人,平均每人每天做25个汽车上的零件;三月份工作30天,共可做零件多少个用两种方法解答109、学校买来5盒皮球,每盒12个,每个6元,共要付出多少元110、碾米机每台一小时碾米1500千克;照这样计算,3台碾米机10小时碾米多少千克用两种方法,列综合式解答111、饲养场养公鸡1500只,母鸡只数是公鸡的4倍,小鸡是母鸡的3倍,有小鸡多少只112、1辆汽车1天运货20啊,4辆汽车5天运货多少吨113、4辆汽车5天共运货400吨,1辆汽车1天运货多少吨114、3辆汽车4次可以运288筐苹果,1辆汽车1次可以运多少筐苹果115、光明中学的团员平整操场,35人3小时平整了1260平方米,平均每人每小时平整多少平方米116、一份稿件共960页,8个打字员共打12小时才完成,平均每个打字员每小时可以打字几页117、每只鸡每天吃饲料4500克,照这样计算,6只鸡5天吃饲料多少千克118、4台碾米机3小时可以碾米4800千克,1台碾米机8小时可以碾米多少千克119、根据条件补充问题,并说出数量关系;有5个教室,每个教室有8盏灯,王平同学每天早晨跑500米,跑了5天,8个打字员共打字1600个,三年级有160人,四年级有114人,120、一辆汽车第一天行53千米,第二天行58千米,第三天上午行30千米,下午行27千米;平均每天行多少千米121、光明小学五年级3个班为灾区人民捐款750元,六年级4个班为灾区人民捐款1210元;平均每个年级捐款多少元这两个年级平均每班捐款多少元122、小荣家养鸭45只,养的鸡比鸭多90只;小荣家养鸡多少只123\有红花10朵,黄花的朵数比红花的4倍多4朵,两种花共有多少朵问:要求两种花共有多少朵,你怎样分析变问题:红花比黄花少多少朵124、学校有篮球12个,足球的个数比篮球的2倍少5个, 足球的个数比篮球多几个两种球共多少个125、绵羊可以活20年,老虎可以活50年,海龟活的年数比绵羊和老虎活的年数之和的2倍还多20年,海龟能活多少年问:你认为哪句话关键126、小明读课外书120也,小华读的页数比小名读得2倍多10页,小玲读的页数是小华读得2倍,小玲读书多少页。

20．18.84平方米
21．20千克
22．100千米/小时
23． ；96.2%
24．320.28米
25．2835元
26．（1）39克；
（2）180克；32.1克
27．240个
28．200箱
29．浓度20%的50克，浓度18%的40克，浓度16%的10克
解答：
15．某品牌电脑的单价是6300元，国庆进行促销活动，先降价10%销售，后来又在此基础上涨价10%，最终售价比降价前高还是低？高或低百分之几？
16．运输公司前年耗油100吨，去年耗油80吨。
（1）去年耗油是前年的百分之几？
（2）去年比前年节油百分之几？
17．苗圃种植了一批杨树共200棵，结果成活率是95%。成活了多少棵？
26．咖啡中的蛋白质含量为60%，脂肪含量为13%，碳水化合物含量为10.7%。
（1）300克咖啡中共有脂肪多少克？
（2）300克咖啡中共有蛋白质、碳水化合物各多少克？
27．国庆假期，妈妈给小红布置了练习毛笔字的任务，第一天完成了全部任务的 ，第二天完成了全部任务的25%，还剩140个字没有练。小红的任务是多少个字？
人教版六年级上册数学百分数（一）应用题综合训练
1．为了提高绿化率，金色阳光小区种植了200棵广玉兰。这批广玉兰成活了多少棵？
2．饲养小组养了36只白兔，12只灰兔，白兔和灰兔分别占总只数的百分之几？
3．小明看一本书，第一天看了全书的20%，第二天看了全书的 ，还剩下120页，这本书共有多少页？
4．师傅和徒弟合作加工一批零件，师傅加工了50个，但是有4%不合格，徒弟加工了30个，但是有10%不合格，那么师徒二人加工的这批零件的合格率是百分之多少？
21．一袋面粉，用去 后，再加进7千克，这时袋里的面粉正好是原来面粉的75%。这袋面粉原有多少千克？