三角函数图像变换顺序详解全面)

三角函数的图像变换三角函数是数学中重要的一类函数，包括正弦函数、余弦函数、正切函数等。

它们在图像上呈现出规律性的波动变化，而通过对这些函数进行图像的平移、缩放、翻转等操作，可以得到各种不同形态的函数图像。

本文将介绍三角函数的图像变换过程，并探讨不同变换对函数图像的影响。

正弦函数的图像变换正弦函数 $y = \\sin(x)$ 是一种周期性函数，其图像在 $[-\\pi, \\pi]$ 区间内呈现出波浪状的变化。

对正弦函数进行图像变换可以通过调整函数中的关键参数来实现。

平移平移是一种简单的图像变换操作，可以沿着横轴和纵轴分别对函数图像进行移动。

对于正弦函数 $y=\\sin(x)$ 来说，平移操作可以表示为 $y = \\sin(x - a)$，其中a为平移距离。

当a>0时，函数图像向右平移；当a<0时，函数图像向左平移。

缩放缩放是改变函数图像振幅的一种常见操作。

对于正弦函数$y=\\sin(x)$，可以通过调整函数中的系数来实现振幅的变化。

例如，当 $y=2\\sin(x)$ 时，函数图像的振幅将变为原来的两倍；当 $y=\\frac{1}{2}\\sin(x)$ 时，函数图像的振幅将缩小为原来的一半。

翻转翻转是改变函数图像对称性的一种操作。

对于正弦函数$y=\\sin(x)$，可以通过在函数中引入负号来实现翻转操作。

例如，当 $y=-\\sin(x)$ 时，函数图像将在a轴进行翻转。

余弦函数的图像变换余弦函数 $y = \\cos(x)$ 也是一种周期性函数，其图像在$[0, 2\\pi]$ 区间内呈现出波浪状的变化。

对余弦函数进行图像变换同样可以通过平移、缩放、翻转等操作来实现。

平移对于余弦函数 $y=\\cos(x)$，平移操作的表达式为 $y =\\cos(x - a)$，其中a为平移距离。

与正弦函数类似，当a> 0时，函数图像向右平移；当a<0时，函数图像向左平移。

三角函数图像平移变换由y ＝sin x 的图象变换出y ＝sin(ωx ＋ϕ）的图象一般有两个途径，只有区别开这两个途径，才能灵活进行图象变换。

利用图象的变换作图象时，提倡先平移后伸缩，但先伸缩后平移也经常出现无论哪种变形,请切记每一个变换总是对字母x 而言，即图象变换要看“变量"起多大变化，而不是“角变化”多少.途径一：先平移变换再周期变换(伸缩变换）先将y ＝sin x 的图象向左(ϕ＞0)或向右（ϕ＜0＝平移｜ϕ｜个单位,再将图象上各点的横坐标变为原来的ω1倍（ω＞0)，便得y ＝sin(ωx ＋ϕ)的图象. 途径二：先周期变换(伸缩变换)再平移变换。

先将y ＝sin x 的图象上各点的横坐标变为原来的ω1倍(ω＞0)，再沿x 轴向左（ϕ＞0）或向右(ϕ＜0＝平移ωϕ||个单位，便得y ＝sin （ωx ＋ϕ)的图象。

1。

为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像,只需将函数sin 2y x =的图像( A ）A ．向左平移5π12个长度单位B ．向右平移5π12个长度单位 C ．向左平移5π6个长度单位D ．向右平移5π6个长度单位2.要得到函数sin y x =的图象，只需将函数cos y x π⎛⎫=- ⎪3⎝⎭的图象（ D ）A ．向右平移π6个单位 B ．向右平移π3个单位 C ．向左平移π3个单位 D ．向左平移π6个单位3.为了得到函数)62sin(π-=x y 的图象，可以将函数x y 2cos =的图象（ B ）(A ）向右平移6π个单位长度 （B)向右平移3π个单位长度(C)向左平移6π个单位长度 （D)向左平移3π个单位长度4.把函数sin y x =（x R ∈）的图象上所有点向左平行移动3π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数是CA sin(2)3y x π=-，x R ∈B sin()26x y π=+，x R ∈C sin(2)3y x π=+，x R ∈D sin(2)32y x π=+,x R ∈5.为了得到函数sin(2)3y x π=-的图像，只需把函数sin(2)6y x π=+的图像B（A)向左平移4π个长度单位 （B ）向右平移4π个长度单位 （C ）向左平移2π个长度单位 （D ）向右平移2π个长度单位6.已知函数()sin()(,0)4f x x x R πϖϖ=+∈>的最小正周期为π，为了得到函数()cos g x x ϖ=的图象，只要将()y f x =的图象AA 向左平移8π个单位长度 B 向右平移8π个单位长度 C 向左平移4π个单位长度 D 向右平移4π个单位长度7。

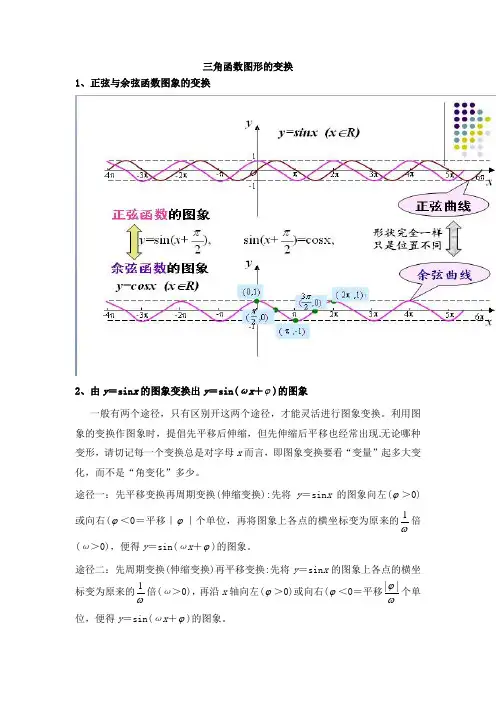
三角函数图形的变换1、正弦与余弦函数图象的变换2、由y ＝sin x 的图象变换出y ＝sin(ωx ＋ϕ)的图象一般有两个途径，只有区别开这两个途径，才能灵活进行图象变换。

利用图象的变换作图象时，提倡先平移后伸缩，但先伸缩后平移也经常出现无论哪种变形，请切记每一个变换总是对字母x 而言，即图象变换要看“变量”起多大变化，而不是“角变化”多少。

途径一：先平移变换再周期变换(伸缩变换):先将y ＝sin x 的图象向左(ϕ＞0)或向右(ϕ＜0＝平移｜ϕ｜个单位，再将图象上各点的横坐标变为原来的ω1倍(ω＞0)，便得y ＝sin(ωx ＋ϕ)的图象。

途径二：先周期变换(伸缩变换)再平移变换:先将y ＝sin x 的图象上各点的横坐标变为原来的ω1倍(ω＞0)，再沿x 轴向左(ϕ＞0)或向右(ϕ＜0＝平移ωϕ||个单位，便得y ＝sin(ωx ＋ϕ)的图象。

作y =sin x （长度为2π的某闭区间）的图象 得y =sin(x +φ) 的图象得y =sin ωx 的图象 得y =sin(ωx +φ) 的图象 得y =sin(ωx +φ) 的图象 得y =Asin(ωx +φ)的图象，先在一个周期闭区间上再扩充到R 上沿x 轴平 移|φ|个单位 横坐标 伸长或缩短 横坐标伸 长或缩短沿x 轴平 移|ωϕ|个单位 纵坐标伸 长或缩短纵坐标伸 长或缩短【经典例题】图像变换一：左右平移1、把函数R x x y ∈=,sin 图像上所有的点向左平移4π个单位，所得函数的解析式为 _________2、把函数R x x y ∈=,cos 图像上所有的点向右平移5π个单位，所得函数的解析式为 _________图像变换二：纵向伸缩3、对于函数R x x y ∈=,s i n 3的图像是将R x x y ∈=,sin 的图像上所有点的______(“横”或”纵”)坐标______（伸长或缩短）为原来的______而得到的图像。

三角函数b x A y ++=)sin(ϕω的图像变换三角函数的图像变换是历年来高考的重点内容，因此我们有必要对这一问题作一下研究。

下面就三角函数的图像变换的基本题型，做以详细讲析：一、 振幅变换由函数)(x f y =的图像变换为)(x Af y =的图像，其主要的方法是将)(x f y =图像上的各点的纵坐标变为原来的A 倍，即)()(A x Af y x f y =−−−−−−→−=倍纵坐标变为原来的。

例1、要得到)32sin(4π-=x y 的图像，只需将)32sin(π-=x y 的图像( )。

A 、 向上平移4个单位；B 、 将)32sin(π-=x y 图像上的各点的纵坐标变为原来的4倍； C 、 将)32sin(π-=x y 图像上的各点的纵坐标变为原来的4-倍； D 、 向下平移4个位单位。

分析：由题意可知，将)32sin(π-=x y 图像上的各点的纵坐标变为原来的4倍，就可以得到)32sin(4π-=x y 的图像。

故选B 。

二、 周期变换由函数)(x f y =的图像变换为)(x f y ω=的图像，其主要的方法是将)(x f y =图像上的各点的横坐标变为原来的ω1倍，即)()(1x f y x f y ωω=−−−−−−→−=倍横坐标变为原来的。

例2、如何由x y sin =的图像得到x y 2sin 2=的图像。

解：由x y sin =的图像上各点的纵坐标伸长到原来的2倍，得到x y sin 2=的图像，再将x y sin 2=的图像各点的横坐标压缩为原来的21倍，得到x y 2sin 2=的图像。

三、 相位变换(左右平移变换)由函数)(x f y =的图像变换为)(ϕ+=x f y 的图像，其主要的方法是将)(x f y =图像上所有点向左或向右平移ϕ个单位。

即)()(0)(ϕϕϕ+=−−−−−−→−=>x f y x f y 个单位向左平移 )()(0)(ϕϕϕ-=−−−−−−→−=>x f y x f y 个单位向右平移 例3、如何由)32sin(31π+=x y 的图像得到x y sin =的图像。

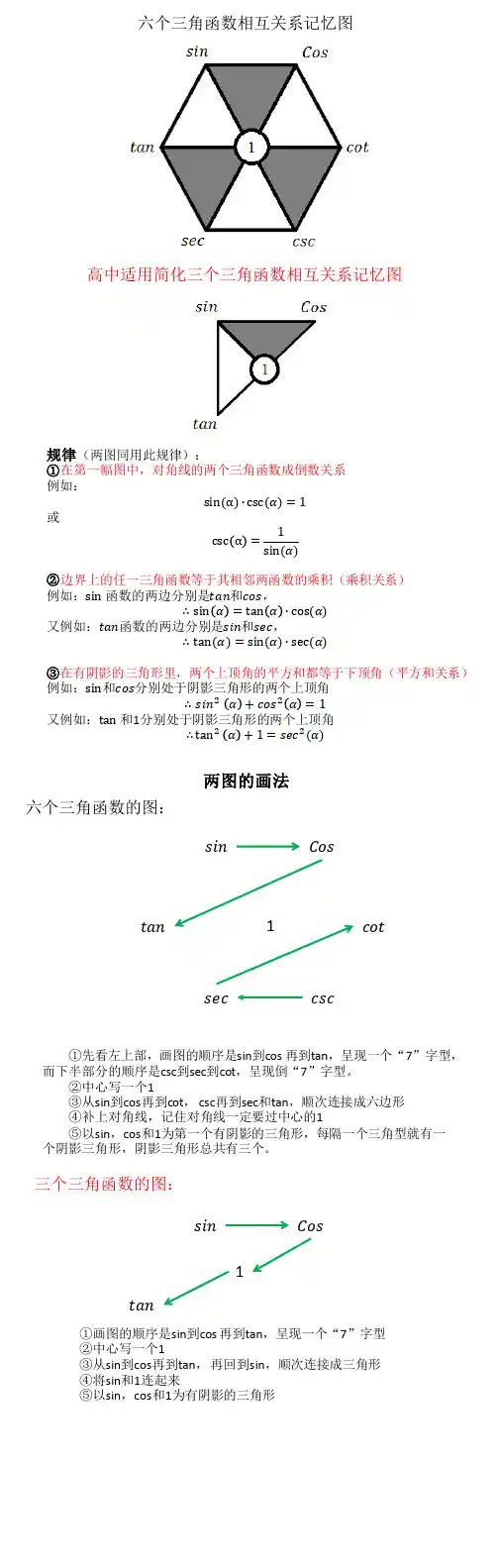
规律（两图同用此规律）：①在第一幅图中，对角线的两个三角函数成倒数关系例如：sin(α)∙csc⁡(α)=1或 csc α=1sin⁡(α) ②边界上的任一三角函数等于其相邻两函数的乘积（乘积关系） 例如：sin⁡函数的两边分别是tan 和cos ，∴sin α=tan α∙cos⁡(α)又例如：tan 函数的两边分别是sin 和sec ，∴tan⁡(α)=sin⁡(α)∙sec⁡(α)③在有阴影的三角形里，两个上顶角的平方和都等于下顶角（平方和关系） 例如：sin 和cos 分别处于阴影三角形的两个上顶角∴sin 2α+cos 2α=1又例如：tan⁡和1分别处于阴影三角形的两个上顶角∴tan 2α+1=sec 2(α)六个三角函数相互关系记忆图高中适用简化三个三角函数相互关系记忆图两图的画法六个三角函数的图：sin Costan cotcscsec ①先看左上部，画图的顺序是sin 到cos 再到tan ，呈现一个“7”字型，而下半部分的顺序是csc 到sec 到cot ，呈现倒“7”字型。

②中心写一个1③从sin 到cos 再到cot ， csc 再到sec 和tan ，顺次连接成六边形④补上对角线，记住对角线一定要过中心的1⑤以sin ，cos 和1为第一个有阴影的三角形，每隔一个三角型就有一个阴影三角形，阴影三角形总共有三个。

1 三个三角函数的图：sin Costan1①画图的顺序是sin 到cos 再到tan ，呈现一个“7”字型②中心写一个1③从sin 到cos 再到tan ， 再回到sin ，顺次连接成三角形④将sin 和1连起来⑤以sin ，cos 和1为有阴影的三角形。

三角函数图像的变换（4月23号）图像变换一：左右平移1、把函数R x x y ∈=,sin 图像上所有的点向左平移4π个单位，所得函数的解析式为 _________ 2、把函数R x x y ∈=,cos 图像上所有的点向右平移5π个单位，所得函数的解析式为 _________图像变换二：纵向伸缩3、对于函数R x x y ∈=,sin 3的图像是将R x x y ∈=,sin 的图像上所有点的______(“横”或”纵”)坐标______（伸长或缩短）为原来的______而得到的图像。

4、由函数R x x y ∈=,s in 4的图像得到R x x y ∈=,sin 的图像，应该是将函数R x x y ∈=,sin 4上所有点的______(“横”或“纵”)坐标______（“伸长”或“缩短”）为原来的______（横坐标不变）而得到的图像。

图像变换三：横向伸缩5、对于函数R x x y ∈=,3sin 的图像是将R x x y ∈=,sin 的图像上所有点的______(“横”或“纵”)坐标______（“伸长”或“缩短”）为原来的______（纵坐标不变）而得到的图像。

图像变换四：综合变换6、用两种方法将函数x y sin =的图像变换为函数)32sin(π+=x y 的图像解：方法一：x y sin =−−−−−→−)(x y 2sin =−−−−→−)()32sin(6(2sin ππ+=⎥⎦⎤⎢⎣⎡+=x x y方法二：xy sin =−−−−→−)()3sin(π+=x y −−−−→−)()32sin(π+=x y总结：方法一： 先伸缩后平移()A →→ϕω 方法二：先平移后伸缩()A →→ωϕ7、用两种方法将函数x y 2sin =的图像变换为函数)4sin(π+=x y 的图像方法一：x y 2sin =−−−−−→−)(x y sin =−−−−→−)()4sin(π+=x y方法二：x y 2sin =−−−−→−)()42sin()8(2sin ππ+=+=x x y −−−−→−)()4sin(π+=x y 8、函数)32sin(3π+=x y 的周期、振幅、初相为________、_________、__________ 9、已知函数()()R x A x A y ∈>>+=,0,0sin ωϕω的最大值是3，最小正周期是72π， 初相是6π，则这个函数的表达式是__________________ 10、已知()x x f sin 1=，()x x f ωsin 2=()0>ω且()x f 2的图像可以看做是把()x f 1的图像上所有点的横坐标缩小到原来的31倍（纵坐标不变）得到的，则=ω________________ 11把函数⎪⎭⎫ ⎝⎛-=32sin πx y 的图像向右平移3π个单位，得到的解析式为____________12、为了得到函数R x x y ∈⎪⎭⎫ ⎝⎛-=,621s in 4π的图像，只需将函数R x x y ∈⎪⎭⎫ ⎝⎛-=,6s in 4π的图像上的所有点____________13、将函数R x x y ∈⎪⎭⎫⎝⎛+=,52sin 3π的图像上的所有点向右平移10π个单位，得到函数()x f 的图像，则()x f 的解析式为________________14、要得到R x x y ∈⎪⎭⎫⎝⎛+=,42cos 3π的图像，只要将R x x y ∈=,2cos 3的图像___________ 15、把函数132s in 2+⎪⎭⎫ ⎝⎛+=πx y 的图像向左平移6π个单位，再向上平移3个单位，所得函数的解析式为__________________ 16、函数⎪⎭⎫⎝⎛-=32sin 3πx y 的图像可由函数x y 2sin 3=的图像经过下列哪种变换得到（ ） A.向右平移3π个单位长度 B.向右平移6π个单位长度C.向左平移个3π单位长度 D.向左平移个6π单位长度17、要得到⎪⎭⎫ ⎝⎛-=42cos πx y 的图像，只要将x y 2sin =的图像（ ）A.向左平移8π个单位长度B.向右平移8π个单位长度C.向左平移个4π单位长度 D.向右平移个4π单位长度18、已知函数242sin 2+⎪⎭⎫ ⎝⎛+=πx y ，求：1函数的周期及单调区间；2函数的图像可由R x x y ∈=,sin 的图像经过怎样的变换而得到三角函数图象变换复习 1.为了得到函数sin(2)3y x π=-的图像，只需把函数sin(2)6y x π=+的图像（ ） （A ）向左平移4π个长度单位（B ）向右平移4π个长度单位（C ）向左平移2π个长度单位（D ）向右平移2π个长度单位2.函数f (x )=2sin x cos x 是（ ）(A)最小正周期为2π的奇函数 （B ）最小正周期为2π的偶函数 (C)最小正周期为π的奇函数（D ）最小正周期为π的偶函数 3.设0ω>,函数sin()23y x πω=++的图像向右平移43π个单位后与原图像重合，则ω的最小值是（ ） （A ）23 （B ） 43 （C ） 32（D ） 3 （1） 将函数y=sin(x+π/6) (x 属于R)的图象上所有的点向左平行移动π/4个单位长度，再把图象上各点的横坐标扩大到原来的2倍（纵坐标不变），则所得到的图象的解析式为( )(A) y=sin(2x+5π/12) (x 属于R) (B) y=sin(x/2+5π/12) (x 属于R) (C) y=sin(x/2+π/12) (x 属于R) (D) y=sin(x/2+5π/24) (x 属于R) 5.下列函数中，周期为π，且在[,]42ππ上为减函数的是（ ） （A ）sin(2)2y x π=+（B ）cos(2)2y x π=+（C ）sin()2y x π=+ （D ）cos()2y x π=+ 6.已知函数()sin (0,)2y x πωϕωϕ=+><的部分图象如题（6）图所示，则（ ）A. ω=1 ϕ=6π B. ω=1 ϕ=- 6π C. ω=2 ϕ= 6π D. ω=2 ϕ= -6π 7.将函数y=sin(x-π/3)的图像上所有的点的横坐标伸长带原来的2倍（纵坐标不变），再将所得的图象向左平移π/3个单位，得到的图象对应的解析式为（ ） (A)y=sin(x/2) (B)y=sin(x/2-π/2)(C) y=sin(x/2-π/6) (D)sin(2x-π/6) 8.将函数sin y x =的图像上所有的点向右平行移动10π个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是（ ）（A ）sin(2)10y x π=-（B ）sin(2)5y x π=- （C ）1sin()210y x π=- （D ）1sin()220y x π=-9.5y Asin x x R 66ππωϕ⎡⎤=∈⎢⎥⎣⎦右图是函数（+）（）在区间-，上的图象，为了得到这个函数的图象，只要将y sin x x R =∈（）的图象上所有的点（ ）(A)向左平移3π个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变(B) 向左平移3π个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变(C) 向左平移6π个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变(D) 向左平移6π个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变7、将函数y=sin2x 的图象向左平移π/4个单位，再向上平移1个单位所得到函数解析式（ ）y=cos2x y=2(cosx)*(cosx) y=1+sin(2x+π/4) y=2(sinx)*(sinx) 11.函数f(x)= 3sin(),24x x R π-∈的最小正周期为（ ）A. 2πB.xC.2πD.4π1．已知函数，则（ ）A ．其最小正周期为2πB ．其图象关于直线对称C ．其图象关于点对称D ．该函数在区间上单调递增2．已知函数f （x ）=cos （x+φ） （0＜φ＜π）在x=时取得最小值，则f （x ）在[﹣π，0]上的单调增区间是（ ） A ．[]B ．[]C ．[，0]D ．[﹣π，]3．将函数f （x ）=2cos2x 的图象向右平移个单位，再向下平移2个单位，则平移后得到图象的解析式是（ ）A ．y=2sin2x ﹣2B ．y=2cos2x ﹣2C ．y=2cos2x+2D ．y=2sin2x+2 4．（2011•惠州模拟）为得到函数的图象，只需将函数y=sin2x 的图象（ ） A ．向左平移个长度单位B ．向右平移个长度单位C ．向左平移个长度单位D ．向右平移个长度单位5．（2009•湖南）将函数y=sinx 的图象向左平移φ（0≤φ＜2π）个单位后，得到函数y=sin （x ﹣）的图象，则φ等于（ ）A ．B ．C ．D ．6．（2007•山东）为了得到函数y=sin （2x ﹣）的图象，可以将函数y=cos2x 的图象（ ） A ．向右平移个单位长度B ．向右平移个单位长度 C ．向左平移个单位长度D ．向左平移个单位长度7．（2009•山东）将函数y=sin2x 的图象向左平移个单位，再向上平移1个单位，所得图象的函数解析式是（ ）A ．y=2cos 2x B ．y=2sin 2x C ．D ．y=cos2x8．有以下四种变换方式： ①向左平行移动个单位长度，再将每个点的横坐标缩短为原来的；②向右平行移动个单位长度，再将每个点的横坐标缩短为原来的；③每个点的横坐标缩短为原来的，再向右平行移动个单位长度；④每个点的横坐标缩短为原来的，再向左平行移动个单位长度．其中能将函数y=cos（）的图象变为函数y=sin（2x+）的图象是（）A．①和④B．①和③C．②和④D．②和③9．将函数y=cosx的图象上所有的点向右平行移动个单位长度，再把所得各点的横坐标缩短到原来的（纵坐标不变），所得图象的函数解析式是（）A．B．C．D．10．（2012•无为县模拟）将函数y=sin2x的图象上所有的点向右平行移动个单位长度，再把所得各点的横坐标缩短到原来的倍（纵坐标不变），则所得函数的图象（）A．关于点对称B．关于直线对称C．关于点对称D．关于直线对称11．将函数的图象向右平行移动个单位长度，再把横坐标缩短为原来的一半，纵坐标伸长为原来的3倍，则所得到的图象的函数解析式是（）A．B．C．D．12．为了得到函数的图象，只需把函数y=sin2x的图象上所有的点_________．13．把函数y=sinx（x∈R）的图象上所有的点向左平行移动个单位长度，再把所得图象上所有点的横坐标缩短到原来的倍（纵坐标不变），得到的图象所表示的函数是_________．14．把y=sinx的图象向左平移个单位，得到函数_________的图象；再把所得图象上的所有点的横坐标伸长到原来的2倍，而纵坐标保持不变，得到函数_________的图象．15．已知函数f（x）=sin（ωx+）（x∈R，ω＞0）的最小正周期为π，为了得到函数g（x）=cos（ωx）的图象，只要将y=f（x）的图象向_________平移_________个单位长度．16．①向左平移，再将横坐标变为原来的；②横坐标变为原来的，向左平移；③横坐标变为原来的，向左平移；④向左平移，横坐标变为原来的，其中能将y=sinx的图象变为y=sin（2x+）的图象的是_________．17．将函数y=sinx的图象上所有的点向右平行移动个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象的函数解析式是_________．18．将函数的图象上所有的点向右平行移动个单位长度，再把所得图象各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象的函数解析式是_________．19．把函数的图象向左平移个单位，再将横坐标缩小为原来的，则其解析式为_________．20．函数y=Asin（ωx+φ）的图象的图象上相邻的最高点与最低点的横坐标的差为2π，则ω=_________．21．直线y=m与函数y=Asin（ωx+ϕ）（ω＞0）有交点，其中三个相邻交点的横坐标分别为2，4，14，则ω的值为_________．22．（2012•朝阳区二模）函数y=2cosx，x∈[0，2π]的单调递增区间是_________．23．函数y=sin（x+）在[﹣2π，2π]内的单调递增区间是_________．24．函数y=sin（x+）在区间[0，]的最小值为_________25．函数y=sinx，x的值域为_________．26．函数y=3sin （x∈[0，π]）的单调减区间是_________．27．函数的值域为_________．28．函数，x∈[﹣2π，2π]的单调递增区间是_________．29．函数（π≤x≤2π）的值域为_________．30．函数，在区间（﹣π，π）上单调递增，则实数φ的取值范围为_________．1．（2010•福建）计算sin137°cos13°+cos103°cos43°的值等于（）A．B．C．D．2．（2004•重庆）sin163°sin223°+sin253°sin313°等于（）A．﹣B．C．﹣D．3．cos275°+cos215°+cos75°•cos15°的值是（）A．B．C．D．4．（2011•郑州二模）计算cos42°cos18°﹣cos48°cos72°的结果等于（）A．B．C．D．5．（2011•江西模拟）计算cos 28° cos17°﹣sin 28° sin17°的结果等于（）A．B．C．D．6．（2010•海淀区一模）sin75°cos30°﹣cos75°sin30°的值为（）A．1B．C．D．7．（2010•成都三模）计算cos45°cos15°﹣sin45°cos75°的结果是（）A．B．C．D．18．若β=α+30°，则sin2α+cos2β+sinαcosβ=（）A．B．C．cos2βD．sin2α9．下列各式化简结果为cosα的是（）A．cos20°cos（α﹣20°）+cos70°sin（α﹣20°）B．cos20°cos（α﹣20°）﹣cos70°sin（α﹣20°）C．cos20°sin（α﹣20°）+cos70°cos（α﹣20°）D．cos20°sin（α﹣20°）﹣cos70°cos（α﹣20°）10．sin43°cos17°+cos43°sin17°的值为（）A．B．C．D．11．sin17°cos227°+sin73°sin47°等于（）A．﹣B．C．﹣D．12．（2011•南通模拟）化简的值为_________．13．（2009•宁波模拟）sin155°cos35°﹣cos25°cos235°=_________．14．sin14°cos16°﹣cos166°sin16°的值是_________．15．sin35°•sin25°﹣cos35°•cos25°的值是_________．16．求值：cos105°cos15°﹣sin105°sin15°=_________．17．计算：cos13°•cos47°+sin13°•cos137°=_________．18．cos40°cos20°﹣sin40°sin20°的值等于_________．19．的值等于_________．20．sin34°sin64°+cos34°sin26°的值是_________．21．函数y=sinx+cosx的单调增区间是_________．22．cos96°cos24°﹣sin96°cos66°=_________．23．cos174°cos156°﹣sin174°sin156°的值为_________．24．函数的最小值为_________．25．cos47°sin13°+sin47°sin77°的值等于_________．26．sin420°cos750°+sin（﹣330°）cos（﹣660°）=_________．27．sin47°cosl3°+sinl3°sin43°的值等于_________．28．cos73°cos13°+cos17°sin13°=_________．29．函数y=sin2x+cos2x的最小正周期是_________．30．sin75°cos30°﹣cos75°sin30°=_________．1．（2013•湖北）将函数的图象向左平移m（m＞0）个单位长度后，所得到的图象关于y 轴对称，则m的最小值是（）A．B．C．D．2．（2012•重庆）=（）A．﹣B．﹣C．D．3．若，，，则cos（α+β）的值等于（）A．B．C．D．4．（2014•孝感二模）函数的最大值是（）A．2 B．1 C．D．5．（2014•云南一模）函数f（x）=sin2x﹣sin（2x+）的最小值为（）A．0 B．﹣1 C．D．﹣2 6．设，则sin2θ=（）A．B．C．D．7．已知，且0°＜α＜90°，则cosα=（）A．B．C．D．8．观察下列等式：13+23=（1+2）2，13+23+33=（1+2+3）2，13+23+33+43=1+2+3+4）2，…，根据上述规律，第四个等式为_________．9．如果一个凸多面体是n棱锥，那么这个凸多面体的所有顶点所确定的直线共有_________条，这些直线中共有f （n）对异面直线，则f（4）=_________；f（n）=_________．（答案用数字或n的解析式表示）10．）方程在区间（0，π）内的解是_________．11．化简：=_________．12．函数在区间[]的最小值为____．13．若，则的取值范围是__14．函数的单调递增区间_________．15．已知，，则sinα=_________．16．函数的单调递减区间为_________．17．方程在（0，π）上的解集是_________．18．（2007•金山区一模）方程sinx+cosx=﹣1在[0，π]内的解为_________．19．（2006•南京一模）在△ABC中，若，则的值为_________．20．若cos（）﹣sinα=，则sin（）=_________．21．y=cos2xcos的单调递减区间是_________．22．锐角α，β满足，则α+β=_________．23．已知cosα=，cosβ=，且α、β为锐角，则cos（α+β）=_________．24．已知tan是第二象限角，则sin（）的值为_________．25．（2012•上饶一模），则f（1）+f（2）+…+f（2012）=_________．26．（2012•东至县模拟）在△ABC中，若sinA=，cosB=，则cosC的值是_________．27．（2011•钟祥市模拟）已知，则的值等于_________．28．（2010•金山区一模）若cosα=﹣，α∈（，π），则sin（α+）=_________．29．（2008•崇明县二模）已知，则=_________．30．已知，其中，则=_________．1．（2011•重庆）已知sinα=+cosα，且α∈（0，），则的值为_________．2．（2008•北京）若角α的终边经过点P（1，﹣2），则tan2α的值为_________．3．（2013•松江区二模）已知，且，则sin2α=_________．4．（2013•日照二模）已知α为第二象限角，，则sin2α=_________．5．（2013•成都二模）已知sinα+cosα=，则sin2α的值为_________．6．（2012•烟台二模）已知sin，则sin2α的值为_________．7．（2012•虹口区一模）已知，则的值等于_________．8．（2012•海淀区一模）若tanα=2，则sin2α=_________．9．已知cosθ=2sinθ，则cos2θ的值为_________．10．（2011•成都一模）已知cosα=，则cos2α=_________．11．（2008•江苏二模）已知cos（α+）=，且，则sin2α=_________．12．若α为锐角，且，则=_________．13．计算：sin10°cos20°sin30°cos40°=_________．14．已知，则sin2α=_________．15．已知=_________．16．若tanα=1则sin2α+cos2α=_________．17．=_________．18．若tan（a﹣）=2，则tan2a=_________．19．已知tanx=2，则=_________．20．已知，则的值等于_________．21．（2011•扬州三模）已知，则cos2θ=_________．22．（2012•上高县模拟）若2sinα+cosα=0，则=_________．23．若=_________．24．若tanθ=2，则2sin2θ﹣sin2θ=_________．25．若x=，则sin4x﹣cos4x=_________．26．若，则=________27．三角函数式的值等于____．28．已知函数f（x）=（Ⅰ）求f（x）的定义域；（Ⅱ）设α是第四象限的角，且tanα=，求f（α）的值．29．已知α∈（），且sinα=；（Ⅰ）求sin（α+）的值；（Ⅱ）求cos（2α+）的值．30．已知tanθ=2．（Ⅰ）求的值；（Ⅱ）求cos2θ的值．1．（2012•辽宁）已知，α∈（0，π），则sin2α=（ ） A ． ﹣1 B ．C ．D ． 12．（2013•江西）若sin=，则cos α=（ ）A ． ﹣B ． ﹣C ．D ．3．（2012•江西）若，则tan2α=（ ） A ． ﹣ B ． C ． ﹣ D ．4．计算1﹣2sin222.5°的结果等于（ ） A ． B ． C ． D ．5．sin15°cos75°+cos15°sin105°等于（ ） A ． 0B ．C ．D ． 16．设0≤x ＜2π，且=sinx ﹣cosx ，则（ ）A ． 0≤x ≤πB ．≤x ≤C ．≤x ≤D ． ≤x ≤7．函数y=2sinx （sinx+cosx ）的最大值为（ ） A ． B ． C ．D ． 28．sin15°cos30°sin75°的值等于（ ） A ．B ．C ．D ．9．已知sina=，则cos （π﹣2a ）=（ ） A ． ﹣B ． ﹣C ．D ．10．已知sin2α=，则cos2（α+）=（ ） A ． B ．C ．D ．11．已知α为第二象限角，，则cos2α=（ ） A ． ﹣B ． ﹣C ．D ．12．（2014•淄博一模）已知tan α=2，那么sin2α的值是（ ） A ． B ． C ． D ．13．（2014•杭州一模）若α∈（，π），且3cos2α=sin （﹣α），则sin2α的值为（ ）A ．B ．C ．D ．14．（2014•贵阳一模）若sin （+α）=，则sin2α等于（ ） A ． ﹣B ．C ． ﹣D ．15．（2013•唐山一模）已知，则 tan2α=（）A ．B ． ﹣C ．D ． ﹣．16．（2013•合肥二模）若tan α=﹣，则cos2α=（ ）A ．B ．C ．D ．17．已知角α的终边经过点（﹣8，﹣6）则sin2α=（ ） A ．B ．C ．D ．18．化简的结果是（ ） A ． 2cos3 B ． 2sin3 C ． ﹣2sin3 D ． ﹣2cos319．已知的值是（） A ．B ．C ．D ．20．设，则（ ）A． c＜a＜b B． b＜c＜a C． a＜b＜c D． b＜a＜c21．若tanα=3，则tan2α的值是（）A．B．C．D．22．sin275°+sin215°+sin75°•sin15°的值是（）A．B．C．D．23．sin15°•cos15°=（）A． 1 B．﹣1 C．D．﹣224．在△ABC中，若sin2A=﹣，则sinA﹣cosA的值为（）A．B．C．D．25．已知sin（π+α）=，则cos2α等于（）A．B．﹣ C．D．﹣26．（sin22.5°+cos22.5°）（sin22.5°﹣cos22.5°）=（）A．﹣B．C．D．﹣27．sin15°cos165°的值是（）A．B．C．D．28．已知，则sin4θ+cos4θ=．（）A．B．C． 1 D．﹣29．（2013•蚌埠二模）已知sinα=，则cos2α=（）A．B．C．﹣D．30．已知α为锐角，，则tan =（）A．B．C．﹣3 D．﹣21．若角α的终边经过点P（1，﹣2），则tan2α的值为_________．2．函数y=2sinxcosx﹣1，x∈R的值域是_________．3．函数y=sin2xcos2x的最小正周期是_________．4．已知sinα+cosα=，则cos4α=_________．5．已知α∈[，π]，sinα=，则sin2α=_____．6．已知，则cos2α=_________．7．（2013•普陀区二模）若且sin2θ＜0，则tanθ=_________．8．（2013•松江区二模）已知，且，则sin2α=_________．9．（2013•成都二模）已知sinα+cosα=，则sin2α的值为_________．10．（2012•蓝山县模拟）函数y=的最小正周期是_________．11．（2011•成都一模）已知α是第四象限的角，且，则cosα=_________．12．（2011•成都一模）已知cosα=，则cos2α=_________．13．（2012•丰台区二模）已知cosθ=2sinθ，则cos2θ的值为_________．14．（2009•朝阳区一模）若，则cos2θ等于_________．15．（2004•河西区一模）化简cos275°的值是_________．16．若α为锐角，且，则=_________．17．已知cosx﹣sinx=，则sin2x的值为______．18．已知，则sin2θ的值为_________．19．函数y=sin2x﹣2sinxcosx﹣cos2x（x∈R）的单调递增区间为_________．20．计算：cos475°﹣sin475°=_________．21．若tanα=1则sin2α+cos2α=_________．22．=_________．23．2cos215°﹣cos30°=_________．24．（2014•烟台一模）已知tanα=2，则=_________．25．（2013•北京）已知函数f（x）=．（Ⅰ）求f（x）的最小正周期及最大值；（Ⅱ）若α∈（，π），且f（α）=，求α的值．26．已知函数f（x）=2sinxcosx+cos2x（Ⅰ）求的值；（Ⅱ）设α∈（0，π），，求sinα的值、27．解方程cos2x=cosx+sinx，求x的值．28．（2013•荆门模拟）已知函数（1）若a=﹣1，求f（x）的单调增区间；（2）若x∈[0，π]时，f（x）的值域是[5，8]，求a，b的值．29．（2013•惠州模拟）已知函数f（x）=1+sinx•cosx．（1）求函数f（x）的最小正周期和最小值；（2）若tanx=，x∈（0，），求f（﹣）的值．30．（2013•海淀区一模）已知函数f（x）=2﹣（sinx﹣cosx）2．（Ⅰ）求f（）的值和f（x）的最小正周期；（Ⅱ）求函数在区间[﹣，]上的最大值和最小值．1．对任何的值等于（）A．B．C．D．2．若，则角θ的终边落在直线（）上A．24x﹣7y=0 B．24x+7y=0 C．7x+24y=0 D．7x﹣24y=03．已知θ为第二象限角，sin（π﹣θ）=，cos的值为（）A．B．C．±D．±4．已知180°＜α＜360°，则的值等于（）A．B．C．D．5．若2sinx=1+cosx，则的值等于（）A．B．或不存在C．2 D．2或6．直线2x+1=0的倾斜角为α，则=（）A．1 B．C．D．07．若sin74°=m，则cos8°=（）A．B．C．D．8．已知，cos2x=a，则sinx=（）A．B．C．D．9．已知cosx+sinx=1，则等于（）A．0 B．1 C．﹣1 D．0或110．已知角α为第二象限角且，则=（）A．B．C．D．11．若cosα=﹣，α是第三象限角，则=（）A．2 B．C．﹣2 D．﹣12．已知π＜α＜2π，且，则=（）A．B．C．D．13．已知cosθ=﹣，θ∈（﹣π，0），则sin+cos=（）A．B．±C．D．﹣14．已知等腰三角形顶角的余弦值为，则底角的余弦值为（）A．B．C．D．15．已知，则cos（π﹣α）=_________．16．（2013•普陀区二模）若且sin2θ＜0，则=_________．17．（2012•温州二模）已知cos2=a，则cos1=_________．（用a表示）18．若，，则的值是_________．19．若，且，则=_________．20．在△ABC中，若，则=_________．21．已知，，则=_________．22．已知=﹣，则sinα等于_________．23．已知，则cosθ=_________．24．如果，则的值为_________．25．设2＜Z，且，．（1）求cosα的值；（2）证明：．26．已知为第四象限角，求的值．27．化简：+．。

高中数学三角函数图像变换在高中数学的学习中，三角函数图像变换是一个非常重要的知识点，它不仅是高考的重点，也是理解三角函数性质和应用的关键。

对于很多同学来说，这部分内容可能会感到有些抽象和难以掌握，但只要我们深入理解其本质和规律，就能够轻松应对。

首先，我们来了解一下三角函数的基本图像。

以正弦函数 y ＝ sin x 为例，它的图像是一个周期为2π 的波浪形曲线，在区间0, 2π 内，经过点（0, 0)、（π/2, 1)、（π, 0)、（3π/2, －1) 和（2π, 0)。

余弦函数 y＝ cos x 的图像也是一个周期为2π 的曲线，与正弦函数的形状相似，但在 x ＝ 0 时，函数值为 1。

接下来，我们看看三角函数图像的平移变换。

平移变换是指将三角函数的图像在坐标轴上进行水平或垂直移动。

比如，对于函数 y ＝sin(x ＋φ) （φ ＞ 0），它的图像是将 y ＝ sin x 的图像向左平移φ 个单位；而对于函数 y ＝sin(x φ) （φ ＞ 0），则是将 y ＝ sin x 的图像向右平移φ 个单位。

同样，对于余弦函数也有类似的规律。

再说说伸缩变换。

伸缩变换包括沿 x 轴和 y 轴的伸缩。

对于函数 y＝sin ωx （ω ＞ 0），当ω ＞ 1 时，函数图像在 x 轴方向上被压缩；当 0 ＜ω ＜ 1 时，函数图像在 x 轴方向上被拉伸。

而对于函数 y ＝ A sin x （A ＞ 0），当 A ＞ 1 时，函数图像在 y 轴方向上被拉伸；当 0＜ A ＜ 1 时，函数图像在 y 轴方向上被压缩。

那么，如何理解这些变换呢？我们可以通过实际的例子来感受一下。

假设我们有一个摩天轮，它的高度与时间的关系可以用正弦函数来表示。

如果摩天轮的转动速度加快，就相当于在x 轴方向上进行了压缩；如果摩天轮整体向上移动了一段距离，就相当于在 y 轴方向上进行了平移。

在解决三角函数图像变换的问题时，我们需要注意以下几点。

三角函数图像变换总结三角函数是高中数学中非常重要的一个概念，它在几何、物理、工程等领域中有着广泛的应用。

在学习三角函数时，我们经常会接触到三角函数的图像变换。

图像变换是指通过对原始函数的一系列操作，得到一个新的函数的过程。

一、平移变换平移变换是指将函数的图像沿着横轴或纵轴方向平移一定的距离。

当我们将函数沿着横轴平移时，可以通过将自变量加上一个常数来实现。

例如，若将函数f(x)沿着横轴向右平移a个单位，则新函数为f(x-a)。

同样，当我们将函数沿着纵轴平移时，可以通过将因变量加上一个常数来实现。

二、伸缩变换伸缩变换是指通过改变函数的自变量或因变量的取值范围来改变函数的图像形状。

当我们将函数的自变量进行伸缩时，可以通过改变自变量的比例系数来实现。

例如，若将函数f(x)的自变量x进行伸缩，新函数为f(kx)，其中k是一个正常数。

当k 大于1时，函数图像会水平压缩；当0<k<1时，函数图像会水平拉伸。

同样，我们可以将函数的因变量进行伸缩，通过改变因变量的比例系数来实现。

三、翻折变换翻折变换是指通过改变函数的自变量或因变量的正负号来改变函数的图像形状。

当我们将函数的自变量进行翻折时，可以通过将自变量取相反数来实现。

例如，若将函数f(x)的自变量进行翻折，新函数为f(-x)。

同样，我们可以将函数的因变量进行翻折，通过将因变量取相反数来实现。

四、迭加变换迭加变换是指将多个变换效果叠加在一起，从而得到一个新的函数的图像。

例如，我们可以将平移、伸缩和翻折等变换操作应用于原始函数，得到一个经过多次变换的新函数的图像。

通过迭加变换，我们可以获得更加丰富多样的函数图像。

总结起来，三角函数的图像变换是通过对函数的自变量和因变量进行平移、伸缩、翻折等操作来改变函数的图像形状。

通过合理地应用这些图像变换，我们可以更好地理解和应用三角函数，并在解决实际问题时提供便利。

因此，掌握三角函数的图像变换是非常重要的数学技能之一，也是我们在数学学习中需要重点关注和掌握的内容之一。

三角函数的图象变换——由y ＝sin x 的图象变换出y ＝sin(ωx ＋ϕ)的图象 初学习三角函数的读者，对三角函数图象的水平方向的平移和伸缩变换感到困难重重，笔者针对此问题提供给读者快速而简便的方法，供选用和实践．指点迷津由y ＝sin x 的图象变换出y ＝sin(ωx ＋ϕ)的图象一般有两个途径：途径一：先平移变换再周期变换(伸缩变换)先将y ＝sin x 的图象向左(ϕ＞0)或向右(ϕ＜0)平移｜ϕ｜个单位，再将图象上各点的横坐标变为原来的ω1倍(ω＞0)，便得y ＝sin(ωx ＋ϕ)途径二：先周期变换(伸缩变换)再平移变换先将y ＝sin x 的图象上各点的横坐标变为原来的ω1倍(ω＞0),再沿x 轴向左(ϕ＞0)或向右（ϕ＜0）平移ωϕ||个单位，便得y ＝sin(ωx ＋ϕ)试试身手例题1、已知函数y=cos 2x+3sinxcosx+1（x ∈R ）,该函数的图象可由y=sinx(x ∈R)的图象经过怎样的平移和伸缩变换得到?【分析】首先，要将函数解析式化简，化成由y ＝A sin(ωx ＋ϕ)＋B 的形式，再利用作函数的图像的两个方法“五点法”与图像变换的方法即可求得.【答案】 y=cos 2x+3sinxcosx+1=21cos2x+23sin2x+43=sin(2x+6π)+43.(3)解法1:将函数的图象依次作如下变换:函数y=sinx 的图象−−−−−−−−→−个单位向左平移6π函数y=sin(x+6π)的图象−−−−−−−−−−−−−−−−−−→−)(21纵坐标不变倍的各点横坐标缩短到原来函数y=sin(2x+6π)的图象.即函数y=cos 2x+3sinxcosx+1（x ∈R ）的图象.解法2: 函数y=sinx 的图象−−−−−−−−−−−−−−−−−−→−)(21纵坐标不变倍的各点横坐标缩短到原来函数y=sin2x 的图象−−−−−−−−→−个单位向左平移12π函数y=sin(2x+6π)的图象.即函数y=cos 2x+3sinxcosx+1（x ∈R ）的图象.巩固练习练习1、已知函数)62sin(21π+=x y 的图象可由x y sin =的图象经过怎样的变换而得到？例题2、已知函数x ∈R.（1）当函数y 取得最大值时，求自变量x 的集合； （2）该函数的图像可由y=sinx(x ∈R)的图像经过怎样的平移和伸缩变换得到？【分析】首先，要将函数解析式化简，化成由y ＝A sin(ωx＋ )＋B的形式，再利用图像变换的方法即可求得.【答案】（1）y取得最大值必须且只需即k∈Z.所以当函数y取得最大值时，自变量x的集合为.（2）将函数y=sinx依次进行如下变换：(i)把函数y=sinx的图像向左平移，得到函数的图像；(ii)把得到的图像上各点横坐标缩短到原来的倍（纵坐标不变），得到函数的图像；(iii)把得到的图像上各点纵坐标缩短到原来的倍（横坐标不变），得到函数的图像；(IV)把得到的图像向上平移个单位长度，得到函数的图像；综上得到函数的图像.【点评】应用三角公式，将已知函数式化成一个角[即]的简单函数解析式，便可讨论其最值，本题的解答以相应的图像变换给以详细说明，要理解掌握.小试身手1．已知函数y=tan(2x+φ)的图象过点(0,12π)，则φ的值可以是()A -6πB 6πC 12π-D 12π2．要得到函数x y cos 2=的图象，只需将函数)42sin(2π+=x y 的图象上所有的点的（）(A)横坐标缩短到原来的21倍（纵坐标不变）,再向左平行移动8π个单位长度(B)横坐标缩短到原来的21倍（纵坐标不变），再向右平行移动4π个单位长度(C)横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动4π个单位长度(D)横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动8π个单位长度3. 将函数sin (0)y x ωω=>的图象按向量,06a π⎛⎫=- ⎪⎝⎭平移，平移后的图象如图所示，则平移后的图象所对应函数的解析式是A ．sin()6y x π=+ B ．sin()6y x π=-C ．sin(2)3y x π=+ D ．sin(2)3y x π=-4． 已知R a ∈，函数R x a x x f ∈-=|,|sin )(为奇函数，则a ＝（A ）0 （B ）1 （C ）－1 （D ）±1.5． 为了得到函数R x x y ∈+=),63sin(2π的图像，只需把函数R x x y ∈=,sin 2的图像上所有的点（A ）向左平移6π个单位长度，再把所得各点的横坐标缩短到原来的31倍（纵坐标不变） （B ）向右平移6π个单位长度，再把所得各点的横坐标缩短到原来的31倍（纵坐标不变） （C ）向左平移6π个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）把所得（D ）向右平移6π个单位长度，再各点的横坐标伸长到原来的3倍（纵坐标不变）.6． 下列函数中，图象的一部分如右图所示的是（A ）sin 6y x π⎛⎫=+ ⎪⎝⎭（B ）sin 26y x π⎛⎫=- ⎪⎝⎭（C ）cos 43y x π⎛⎫=- ⎪⎝⎭（D ）cos 26y x π⎛⎫=- ⎪⎝⎭.1. 【答案】代入点的坐标即可求得答案为A2. 【答案】 由函数s i n ,y x x R =∈的图象经过变换得到函数sin(),y A x x R ωφ=+∈（1）．y=Asinx ，x ∈R(A>0且A ≠1)的图象可以看作把正弦曲线上的所有点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A 倍（2）函数y=sin ωx, x ∈R (ω>0且ω≠1)的图象，可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的ω1倍（纵坐标不变）（3）函数y ＝sin(x ＋ϕ)，x ∈R (其中ϕ≠0)的图象，可以看作把正弦曲线上所有点向左(当ϕ＞0时)或向右(当ϕ＜0时＝平行移动｜ϕ｜个单位长度而得到 (用平移法注意讲清方向：“加左”“减右”)，可以先平移变换后伸缩变换，也可以先伸缩变换后平移变换，但注意：先伸缩时，平移的单位把x 前面的系数提取出来.运用以上知识即可求得答案为C3. 【答案】将函数sin (0)y x ωω=>的图象按向量,06a π⎛⎫=- ⎪⎝⎭平移，平移后的图象所对应的解析式为sin ()6y x πω=+，由图象知，73()1262πππω+=，所以2ω=，因此选C. 4．【答案】解法1由题意可知，()()f x f x =--得a=0解法2：函数的定义域为R,又f(x)为奇函数,故其图象必过原点即f(0)=0,所以得a=0,解法3由f(x)是奇函数图象法函数画出()R x a x x f ∈-=,sin 的图象选A5．【答案】先将R x x y ∈=,sin 2的图象向左平移6π个单位长度，得到函数2sin(),6y x x R π=+∈的图象，再把所得图象上各点的横坐标伸长到原来的3倍（纵坐标不变）得到函数R x x y ∈+=),63sin(2π的图像，选择C.6．【答案】从图象看出，41T=1264πππ+=，所以函数的最小正周期为π，函数应为y=sin 2x向左平移了6π个单位，即s i n 2()6y x π=+=sin(2)cos(2)cos(2)3236x x x ππππ+=-++=-，选D.。

三角函数的图像的变换口诀解读变T 数倒系数议，变A 伸压 y 无疑， 变φ 要把系数提，正φ 左进负右移．周期变换是通过改变x 的系数来实现的，即周期T 的变化只与ω有关而与φ无关．这是因为ωπ2=T，故要使周期扩大或缩小m (m >0) 倍，则须用xm1去代原式中的x (纵坐标不变)，故有“变T 数倒系数议”之说．相位φ变换实质上就是将函数的图像向左或向右平移．当先作周期变换后作相位变换时，须提出系数ω，这是因为周期变化时改变了x 的值，此时其初相位（非0初相）同时也改变相应得到改变，且改变的倍数相同．当先作相位变换后作周期变换，由于此时x 的系数为1，系数提不提无影响，为了统一记忆我们也视为提出系数“1”．因而有“变φ要把系数提”之说．三角函数图像的周期﹑振幅﹑相位等变换的问题是历年高考中常考查的内容．对此类命题的求解，无论三种变换怎样摆设，先要弄清哪是原函数的图像，哪是新函数的图像，再据本歌诀所述，很快就可得到解决．例1 为了得到 y =)62sin(π-x 的图像，可以将函数 y = cos2x 的图像 (2004年高考) ( )(A)向右平移6π个单位长度 (B)向右平移3π个单位长度(C)向左平移6π个单位长度 (D) 向左平移3π个单位长度解法1 ∵ y = cos2x =)4(2sin )22sin(ππ+=+x x , 而 y =]3)4[(2sin )62sin(πππ-+=-x x ，由此可得 只须将函数y = cos2x 的图像向右平移3π个单位长度即可．故选(B)．解法2 ∵ y =)62sin(π-x )622cos(ππx +-=，即y )3(2cos π-=x , 而已知的函数为y = cos2x ,由此可得，须将函数y = cos2x 的图像向右平3π个单位即可．故选(B)．点评 由于当ωϕ-=x 时, 相位0=+ϕωx ．因而，我们可称此时的相位为零相位．由此可见，在作相位变换时，其平移的数值与方向是由两个0相位对应的x 值的差来决定的．对于本题而言，由于两个0相位对应的x 的值分别为12π与4π-，故所作的平移就是要将已知函数的0相位对应的点)0 ,4(π-移到点)0 12(，π处．易知要平移的数值是：3)4(12πππ=--，方向是向右的．显然这一方法就是“五点作图法”中的第一零点判断法．例2 已知函数 f (x ) =)5sin(2π+x (x ∈R ) 的图像为C, 函数 y =)52sin(π-x (x ∈R ) 的图像为C 1, 为了得到C 1，只需把C 上所有的点先向右平移 ，再将 ． ( )(A)52π个单位，横、纵坐标都缩短到原来的21(B)52π个单位，横、纵坐标都伸长到原来的2倍(C)5π个单位，横、纵坐标都缩短到原来的21 (D)5π个单位，横、纵坐标都伸长到原来的2倍解 ∵ 要求的变换是先作平移变换，后作周期变换，再作振幅变换．故将函数y ＝)5sin(2π+x 的图像向右平移52π个单位, 得到)5sin(2)525sin(2πππ-=-+=x x y的图像．再将此图像的横坐标缩小到原来的一半，得到y =2)52sin(π-x 的图像．最后将其纵坐标缩小到原来的一半，即可得到y =)52sin(π-x 的图像．故选(A)．点评 本题要求先作相位变换，后作周期变换，再作振幅变换，且原函数中x 的系数为“1”,明确这一点是非常重要的．。

高中三角函数的像变换三角函数是数学中常见的函数形式，它们在数学和物理等领域中有着广泛的应用。

像变换是对函数图像进行的一种变换操作，可以通过变换操作来改变原始函数图像的形态和位置。

在高中数学中，三角函数的像变换是一个重要的概念，掌握它可以帮助我们更好地理解和应用三角函数。

一、平移变换平移变换是一种保持函数形状不变，只改变位置的变换操作。

对于三角函数来说，平移变换可以分为水平平移和垂直平移两种类型。

1. 水平平移水平平移是将函数图像沿x轴的方向移动，可以使函数图像向左或向右平移。

数学上，水平平移的量可以用常数c表示。

对于三角函数来说：- 正弦函数y = sin(x + c)的图像向左平移c个单位；- 余弦函数y = cos(x + c)的图像向右平移c个单位；- 正切函数y = tan(x + c)的图像向左平移c个单位。

2. 垂直平移垂直平移是将函数图像沿y轴的方向移动，可以使函数图像向上或向下平移。

数学上，垂直平移的量可以用常数d表示。

对于三角函数来说：- 正弦函数y = sin(x) + d的图像向上平移d个单位；- 余弦函数y = cos(x) + d的图像向上平移d个单位；- 正切函数y = tan(x) + d的图像向上平移d个单位。

二、伸缩变换伸缩变换是一种改变函数图像形状和大小的变换操作。

对于三角函数来说，伸缩变换可以分为水平伸缩和垂直伸缩两种类型。

1. 水平伸缩水平伸缩是通过改变自变量x的取值范围来改变函数图像的形状。

数学上，水平伸缩的量可以用常数a表示。

对于三角函数来说：- 正弦函数y = sin(ax)的自变量x的取值范围变为原来的1/a倍，图像被水平挤压；- 余弦函数y = cos(ax)的自变量x的取值范围变为原来的1/a倍，图像被水平挤压；- 正切函数y = tan(ax)的自变量x的取值范围变为原来的1/a倍，图像被水平挤压。

2. 垂直伸缩垂直伸缩是通过改变因变量y的取值范围来改变函数图像的形状和大小。

三角函数图像的变换1．函数y=Asin（ωx+φ）的图象变换函数y=sin x的图象变换得到y=Asin（ωx+φ）（A＞0，ω＞0）的图象的步骤两种变换的差异先相位变换再周期变换（伸缩变换），平移的量是|φ|个单位；而先周期变换（伸缩变换）再相位变换，平移的量是（ω＞0）个单位．原因是相位变换和周期变换都是针对x而言的．【小黄老师说】1．一个技巧列表技巧：表中“五点”中相邻两点的横向距离均为，利用这一结论可以较快地写出“五点”的坐标．2．两个区别（1）振幅A与函数y=Asin （ωx+φ）+b的最大值，最小值的区别：最大值M=A+b，最小值m=﹣A+b，故A=．（2）由y=sin x变换到y=Asin （ωx+φ）先变周期与先变相位的（左、右）平移的区别：由y=sin x的图象变换到y=Asin （ωx+φ）的图象，两种变换的区别：先相位变换再周期变换（伸缩变换），平移的量是|φ|个单位；而先周期变换（伸缩变换）再相位变换，平移的量是（ω＞0）个单位．原因在于相位变换和周期变换都是针对x而言，即x本身加减多少值，而不是依赖于ωx加减多少值．例1、（2018•通渭县模拟）函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜）的图象如图所示，为了得到y=cos2x的图象，则只要将f（x）的图象（）A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度例2、（2018•全国）要得到y=cosx，则要将y=sinx（）A．向左平移π个单位B．向右平移π个单位C．向左平移个单位D．向右平移个单位例3、（2018•榆林一模）已知曲线，则下列说法正确的是（）A．把C1上各点横坐标伸长到原来的2倍，再把得到的曲线向右平移，得到曲线C2B．把C1上各点横坐标伸长到原来的2倍，再把得到的曲线向右平移，得到曲线C2C．把C1向右平移，再把得到的曲线上各点横坐标缩短到原来的，得到曲线C2D．把C1向右平移，再把得到的曲线上各点横坐标缩短到原来的，得到曲线C21、（2018•金凤区校级三模）已知函数f（x）=Asin（ωx+φ）在一个周期内的图象如图所示，则= .2、（2018•岳阳二模）若将函数y=sin2x的图象向左平移个单位长度，则平移后图象的对称轴方程为（）A．B．C．D．3、（2018•太原三模）已知函数的一个对称中心是（2，0），且f（1）＞f（3），要得到函数f（x）的图象，可将函数的图象（）A．向左平移个单位长度B．向左平移个单位长度C．向右平移个单位长度D．向右平移个单位长度4、（2018•德阳模拟）函数f（x）=sin（2x+φ）（|φ＜|）的图象向左平移个单位后关于原点对称，求函数f（x）在[0，]上的最小值为（）A．﹣B．﹣C．D．5、（2018•齐齐哈尔三模）将函数y=sin（2x+）的图象向右平移个单位长度，则平移后的图象对称中心为（）A．（，0）（k∈Z）B．（﹣，0）（k∈Z）C．（，0）（k∈Z）D．（+，0）（k∈Z）。