钢筋混凝土受扭构件
- 格式:docx
- 大小:43.84 KB
- 文档页数:12






钢筋混凝土受扭构件的破坏形态钢筋混凝土受扭构件是一种常见的结构形式,广泛应用于工程领域。
在受到扭转荷载作用时,钢筋混凝土构件产生破坏。
本文将重点探讨钢筋混凝土受扭构件的破坏形态。
第一,钢筋混凝土受扭构件的破坏形态主要包括开裂、剪切破坏和弯曲破坏三种类型。
开裂是受扭构件破坏的首要表现形式,大多数情况下,开裂是由于剪应力超过材料抗拉强度引起的。
在扭转过程中,开裂逐渐扩展并沿着构件的周边形成裂缝,对构件的承载能力产生一定影响。
第二,剪切破坏是指在扭转荷载作用下,钢筋混凝土构件出现剪切破坏。
通常情况下,剪切破坏是由于主筋与混凝土之间的粘结力不足引起的。
当剪应力达到一定值时,构件内部的剪切破坏将逐渐形成,对构件的承载能力造成严重影响。
第三,弯曲破坏是指在扭转荷载作用下,钢筋混凝土构件出现弯曲形变和破坏。
弯曲破坏是由于扭转荷载引起的应力集中和构件内部应力分布不均匀造成的。
随着荷载的增加,构件会发生弯曲、变形并最终破坏。
综上所述,钢筋混凝土受扭构件的破坏形态主要包括开裂破坏、剪切破坏和弯曲破坏。
这些破坏形态的产生与荷载的作用、材料的性质以及结构的几何形状等因素密切相关。
因此,在设计和施工钢筋混凝土受扭构件时,需要对其承载能力进行充分评估,并采取相应的强化措施,以确保结构的安全可靠。
通过了解钢筋混凝土受扭构件的破坏形态,我们可以更好地理解该类型结构的受力特点,有助于优化设计方案、提高工程质量,并为工程实践提供有价值的参考。
在今后的研究中,我们还需进一步深入探讨钢筋混凝土受扭构件的破坏机理,以不断完善该领域的理论体系,为实际工程应用提供更好的支持。

对于钢筋混凝土受扭构件的受扭纵筋和筋的配筋强度问题,需要分别考虑,以下是具体的内容:1. 受扭纵筋的配筋强度:受扭纵筋是钢筋混凝土受扭构件中承受扭矩的主要钢筋,其配筋应按照要求进行。
受扭纵筋的配筋强度包括了受扭钢筋截面相对于混凝土的弹性极限扭矩和极限扭矩的计算。
- 弹性极限扭矩的计算:按照规范规定计算受扭钢筋的弹性极限扭矩Mu,其中Mu的计算公式为:Mu= Asfy / (1.15γsλs) 其中As是受扭钢筋总面积,fy是钢筋抗拉屈服强度,γs是安全系数,λs是受扭钢筋弯曲等效系数。
- 极限扭矩的计算:按照规范规定计算受扭钢筋的极限扭矩MuRd,其中MuRd 的计算公式为MuRd = ψξβ [Asfy( d - a ) / ΓsLs],其中ψ是考虑钢筋与混凝土间的粘结效应的修正系数,ξ是受扭钢筋的随机偏差系数,β是考虑裂缝宽度影响的修正系数,d是构件截面的有效深度,a是钢筋到构件边缘的距离,Γs是钢筋强度的平均值,Ls是受扭段长度。
2. 筋的配筋强度:另外,为了保证受扭构件的性能,也需要考虑筋的配筋强度。
筋的配筋强度分为两部分,即对筋抗剪的强度和对筋抗弯的强度。
- 对筋抗剪的强度:按规范规定计算对筋的抗剪强度,应满足规范中对受拉纵向钢筋斜截面抗剪强度的规定。
例如,在GB50010-2010中,规定纵向受拉钢筋斜截面抗剪强度Vsb的计算公式如下:Vsb = 0.6fct,bwstr /γv,其中fct,bw是混凝土轴向受拉强度,bwstr是对筋弯折点到截面边缘的距离,γv是安全系数。
- 对筋抗弯的强度:按规范规定计算对筋的抗弯强度,应满足规范中对挠曲变形计算的规定。
例如,在GB50010-2010中,规定任一弯矩作用下,受压区混凝土承载力为Nc = αc[fckAs / γc + fsAs’ / γs],其中αc为影响受压区混凝土应力分布系数,As为对筋面积,As'为与对筋平行的另一组钢筋面积,γc和γs为安全系数。



第4章 钢筋混凝土受扭构件思考题4-1、矩形截面钢筋混凝土纯扭构件的破坏形态与什么因素有关?有哪几种破坏形态?各有什么特点?答:(1)破坏形态与受扭纵筋和受扭箍筋的配筋率有关,还与纵筋与箍筋的配筋强度比ξ有关。
(2)破坏形态:少筋破坏、超筋破坏、部分超筋破坏、适筋破坏。
(3)特点:1)少筋破坏构件是裂缝一旦形成构件马上破坏,开裂扭矩与破坏扭矩相等。
其破坏特征类似于素混凝土构件,明显预兆为脆性破坏。
2) 超筋破坏时钢筋未屈服,构件即由于斜裂缝间的混凝土被压碎而破坏,也无明显预兆为脆性破坏。
3)适筋破坏是受扭纵筋和受扭箍筋的配筋率合适时,当构件三面开裂产生45°斜裂缝后,与斜裂缝相交的受扭钢筋屈服后,还可以继续加荷载,直到混凝土第四面混凝土被压碎,属塑性破坏。
4)部分超筋破坏纵筋与箍筋的配筋强度比不合适时,破坏时纵筋或箍筋未屈服。
其塑性比适筋差,但好于少筋破坏、超筋破坏。
4-2、钢筋混凝土纯扭构件破坏时,在什么条件下,纵向钢筋和箍筋都会先达到屈服强度,然后混凝土才压坏,即产生延性破坏?答:(1)为防止超筋截面尺寸不能太小《规范》规定截面尺寸应满足:T ≤0.2βcfcWt(2)为防止少筋破坏《规范》规定受扭箍筋和纵筋其最小配筋率应满足:受扭箍筋: yv t svt st svt f f bs A 28.02min ,1=≥=ρρ (4-7)受扭纵筋: y t tl stl tl f f Vb T bh A 6.0min ,=≥=ρρ (4-8)(3)为防止部分超筋破坏:《规范》通过限定受扭纵筋与箍筋配筋强度比ζ 的取值,对钢筋用量比进行控制。
ζ=cor st yv y stl u A f sf A 14-3、简述ζ和βt 的意义和取值限制。
称放置,并且四角必须放置答:(1)抗扭纵筋和箍筋其中某一种抗扭钢筋配置过多时,也会使这种钢筋在构件破坏时不能达到屈服强度,为使两种钢筋充分利用,就必须把纵筋和箍筋在数量上和强度上的配比控制在合理的范围之内。
钢筋混凝土受扭构件5.1概述1.矩形截面纯扭构件的受力性能和承载力计算方法;2.剪扭构件的相关性和矩形截面剪扭构件承载力计算方法;3.矩形截面弯、剪、扭构件的承载力计算方法;4.受扭构件的构造要求。
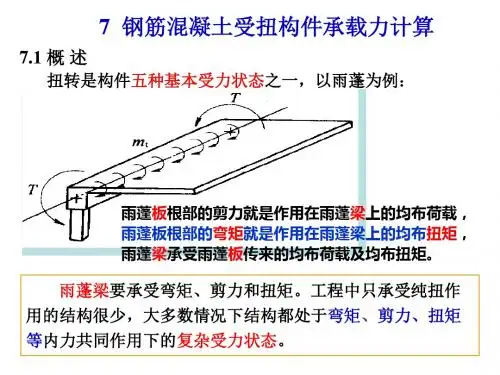
图5-1a所示的悬臂梁,仅在梁端A处承受一扭矩,我们把这种构件称为纯扭构件。
在钢筋混凝土结构中,纯扭构件是很少见的,一般都是扭转和弯曲同时发生。
例如钢筋混凝土雨蓬梁、钢筋混凝土现浇框架的边梁、单层工业厂房中的吊车梁以及平面曲梁或折梁(图5-1b、c)等均属既受扭转又受弯曲的构件。
由于《规范》中关于剪扭、弯扭及弯剪扭构件的承载力计算方法是以构件抗弯、抗剪承载力计算理论和纯扭构件计算理论为基础建立起来的,因此本章首先介绍纯扭构件的计5.2 纯扭构件受力和承载力计算图 5-1 受扭构件示例由材料力学知,在纯扭构件截面中将产生剪应力τ,由于τ的作用将产生主拉应力σtp和主压应力σcp,它们的绝对值都等于τ,即∣σtp∣=∣σcp∣=τ,并且作用在与构件轴线成5-2b),构件随即破坏,破坏具有突然性,属脆性破坏。
5.2.2 素混凝土纯扭构件的承载力计算1.弹性计算理论由材料力学可知,矩形截面匀质弹性材料杆件在扭矩作用下,截面中各点均产生剪应力τ,剪应力的分布规律如图5-3所示。
最大剪应力τmax发生在截面长边的中点,与该点剪应力作用对应的主拉应力σtp和主压应力σcp分别与构件轴线成45方向,其大小为σtp=σcp= τmax当该处主拉应力σtp达到混凝土抗拉极限时,构件将沿与主拉应力σtp垂直方向开裂,其开裂扭矩就是当σtp=τmax=ft时作用在构件上的扭矩。
试验表明,按弹性计算理论来确定混凝土构件的开裂扭矩,比实测值偏小较多。
这说明按弹性计算理论低估了混凝土构件的实际抗扭能力。
2.塑性计算理论对于理想塑性材料的构件,只有当截面上各点的剪应力全部都达到材料的强度极限时,构件才丧失承载力而破坏。
这时截面上剪应力分布如图5-4a所示。
将截面按图5-4b分块计算各部分剪应力的合力和相应力偶,可求出截面的塑性抗扭承载力为式中 T—构件的开裂扭矩; b—矩形截面的短边; h--矩形截面的长边;τmax—截面上的最大剪应力;在纯扭构件中,当σtp=τmax达到混凝土抗拉强度ft时则有τmax=ft于是 T= ftWt (5-1)式中 Wt—截面抗扭塑性抵抗矩,对矩形截面试验分析表明,按塑性理论分析计算出的开裂扭矩略高于实测值。
这说明混凝土并不是理想的塑性材料。
纵上所述可见,素混凝土构件的实际抗扭承载力介于弹性分析和塑性分析结果之间。
根据试验结果偏安全取素混凝土纯扭构件的抗扭承载力为T=0.7ftWt (5-3)公式(5-3)也可近似用来表示计算素混凝土构件的开裂扭矩。
5.2.3 钢筋混凝土纯扭构件的承载力计算1.抗扭钢筋的形式在混凝土构件中配置适当的抗扭钢筋,当混凝土开裂后,可由钢筋继续承担拉力,这对提高构件的抗扭承载力有很大的作用。
由于扭矩在构件中产生的主拉应力与构件轴线成0o因此从受力合理的观点考虑,抗扭钢筋应采用与纵轴线成45角的螺旋钢筋。
但是,45角,这样会给施工带来很多不便,而且当扭矩改变方向后则将失去作用。
在实际工程中,一般都采用由靠近构件表面设置的横向箍筋和沿构件周边均匀对称布置的纵向钢筋共同组成的抗扭钢筋骨架。
它恰好与构件中抗弯钢筋和抗剪钢筋的配置方式相协调。
Wt=(3h-b) (5-2)62.钢筋混凝土纯扭构件的破坏特征试验表明,按照抗扭钢筋配筋率的不同,钢筋混凝土受扭构件的破坏形态可分为三种类型:⑴.少筋破坏当构件抗扭箍筋和纵向钢筋的配置数量过少时,构件在扭矩作用下,首先在剪应力最00大的长边中点处形成45角斜裂缝。
随后,很快地向相邻的其它两个面以45角延伸,在这同时,与斜裂缝相交的抗扭箍筋和纵筋立即屈服或被拉断。
最后,在第四个面上(长边)形成受压面,随着斜裂缝的开展,受压面混凝土被压碎而破坏。
这种破坏形态与受剪的斜拉破坏相似,破坏十分突然,属于脆性破坏。
在设计中应当避免。
⑵.适筋破坏当构件抗扭箍筋和纵向钢筋的配置数量适当时,在扭矩作用下,构件将发生多条45的斜裂缝。
随着扭矩的增加,与主裂缝相交的抗扭箍筋和纵向钢筋达到屈服强度,这条斜裂缝不断开展,并向相邻的两个面延伸,直至在第四个面上受压区的混凝土被压碎而破坏。
这种破形态与受弯构件的适筋梁相似,属于塑性破坏。
钢筋混凝土受扭构件的承载力即以这种破坏形态为计算依据。
⑶.超筋破坏当构件抗扭箍筋和纵向钢筋的配置数量过多时,在扭矩作用下,构件将发生多条45的斜裂缝。
由于抗扭钢筋的配置数量过多,所以构件破坏前钢筋达不到屈服,因而斜裂缝宽度不大。
构件破坏是由于受压区的混凝土被压碎而致。
这种破坏形态与受弯构件的超筋梁相似,属于脆性破坏。
故在设计中应当避免。
为了防止发生少筋破坏,《规范》规定,抗扭箍筋和纵向钢筋的配筋率不得小于各自的最小配筋率,并应符合抗扭钢筋的构造要求。
为了防止发生超筋破坏,《规范》采取限制构件截面尺寸和混凝土强度等级,亦即相当于限制抗扭钢筋的最大配筋率来防止超筋破坏。
3.纯扭构件的承载力计算如前所述,钢筋混凝土受扭构件的承载力计算是以适筋破坏为依据的。
受纯扭的钢筋混凝土构件试验表明,构件的抗扭承载力是由混凝土和抗扭钢筋两部分构成:TU=Tc+ TS (5-4)式中 TU----钢筋混凝土纯扭构件的抗扭承载力;TC----钢筋混凝土纯扭构件混凝土所承受的扭矩,表示为TC=α1ftWt;α1----系数; TS----抗扭箍筋和纵向钢筋所承受的扭矩。
依据试验,抗扭钢筋所承受的扭矩Ts的数值与下述因素有关:⑴与受扭构件纵向钢筋与箍筋的配筋强度比值;⑵截面核心面积Acor; TS可表示为:TS=α式中α2----系数;2yvAcor (5-5) sfyv----抗扭箍筋的抗拉强度设计值;A St1----受扭计算中沿周边所配置箍筋的单肢截面面积;Acor----截面核芯部分面积;Acor= bcorh cor;bcor、h cor----分别为截面核芯的短边和长边,见图5—5。
S----抗扭箍筋的间距;ξ----抗扭纵筋与抗扭箍筋的配筋强度比值;��A stL----抗扭纵筋的截面面积;Ucor----截面核芯的周长, Ucor=2(bcor+h cor) 于是TU=α1ftWt +α2fyvAst1Ucor(5-5)yv钢筋混凝土纯扭构件试验中所得到的数据绘在该坐标系中。
如图5—5示。
《规范》取用试验点的偏下线AB作为钢筋混凝土纯扭构件抗扭承载力。
由图可见,直线AB与纵坐标的截距α1=0.35,直线AB的斜率α2=1.2。
于是,我们便得到矩形截面钢筋混凝土纯扭构件抗扭承载力公式:T≤0.35ftWt+1.2=α1 +α2yvAcorftwtsftwt我们以yvAcor为横坐标,以为纵坐标绘制直角坐标系。
并将已做过的sftwtftwt为了确定式(5—7)中的系数α1、α2的数值,将公式两边同除以ftWt,于是得到:Acor (5-7) syv5.3 剪扭和弯扭构件的承载力计算式中 T----扭矩设计值;ft----混凝土的抗拉强度设计值; Wt----截面的抗扭塑性抵抗矩; fyv---箍筋的抗拉强度设计值;A St1----受扭计算中沿周边所配置箍筋的单肢截面面积; S----抗扭箍筋的间距;Acor---截面核芯部分面积;ξ----抗扭纵筋与抗扭箍筋的配筋强度比值;试验表明,当ξ=0.5~2.0时,构件在破坏前,抗扭纵筋与抗扭箍筋都能够达到屈服强度。
偏于安全,取0.5≤ξ≤1.7,且当ξ≥1.7时,计算取ξ=1.7。
设计中通常取ξ=1.0~1.3。
Acor (5-8) sTu=Tc+Ts Vu=Vc+Vs式中 Tu----有腹筋剪扭构件的抗扭承载力;Tc----有腹筋剪扭构件的混凝土抗扭承载力;Ts----剪扭构件的钢筋抗扭承载力; Vu----有腹筋剪扭构件的抗剪承载力;Vc----有腹筋剪扭构件的混凝土抗剪承载力; Vs----剪扭构件的箍筋抗剪承载力;试验研究结果表明,同时承受剪力和扭矩的剪扭构件,其抗剪承载力和抗扭承载力将随剪力与扭矩的比值变化而变化。
试验指出,构件的抗剪承载力将随扭矩的增加而降低,而构件的抗扭承载力将随剪力的增加而降低。
我们称这种性质为剪扭构件的相关性。
严格地讲,应按有腹筋构件的剪、扭相关性质来建立抗剪和抗扭承载力表达式。
但是,目前的试验和理论分析水平还达不到。
所以,现行规范采取简化的计算方法。
《规范》中引入系数βt来反映剪扭构件的相关性。
βt称为剪扭构件的混凝土受扭承载力降低系数。
�t�0.5≤βt≤1.0对集中荷载作用下的矩形截面混凝土剪扭构件(包括作用有多种荷载,且其中集中荷载对支座截面或节点边缘产生的剪力值占总剪力值的75%以上的情况),式(5-9)改为:1�0.5Tbh0(5-9)�t�式中:λ—计算截面的剪跨比;这样,矩形截面剪扭构件的承载力计算可按以下步骤进行:1�0.2(��1)Tbh0(5-10)1.按抗剪承载力计算需要的抗剪箍筋构件的抗剪承载力按以下公式计算:sV≤(1.5-βt)0.7ftbh0+1.25fyv对集中荷载作用下的矩形截面混凝土剪扭构件(包括作用有多种荷载,且其中集中荷载对支座截面或节点边缘产生的剪力值占总剪力值的75%以上的情况),则改为按下式计算;V≤(1.5-βt)h0 (5-11) s式中1.4≤λ≤3。
同时,系数βt也相应改为式(5-10)计算;2.按抗扭承载力计算需要的抗扭箍筋ftbh0+fyvh0 (5-12)��1ss式中的系数βt分别按公式(5-9)或公式(5-10)计算。
Acor (5-13)T≤0.35�tftWt+1.2yvs构件的抗扭承载力按以下公式计算:5.4 钢筋混凝土弯剪扭构件承载力计算5.3.2 矩形截面弯扭构件承载力计算在受弯同时受扭的构件中,纵向钢筋既要承受弯矩的作用,又要承受扭矩的作用。
因此构件的抗弯能力与抗扭能力之间必定具有相关性,影响这种相关性的因素很多,随着构件截面上部和下部纵筋数量的比值、截面高宽比、纵筋和箍筋的配筋强度比以及沿截面侧边配筋数量的不同,这种弯扭相关性的具体变化规律都有所不同。
要得到其较准确得计算公式目前还很困难。
现行《规范》对弯扭构件采用简便实用的“叠加法”进行计算,即对构件截面先分别按抗弯和抗扭进行计算,然后将所需的纵向钢筋按图5—7所示方式叠加。
3.按照叠加原则计算抗剪扭总的箍筋用量= +sss在实际工程中,钢筋混凝土受扭构件大多数都是同时受有弯矩、剪力和扭矩作用的弯剪扭构件。
为了简化计算,现行《规范》对弯剪扭构件采用“叠加法”进行计算,即其纵向钢筋截面面积由抗弯承载力和抗扭承载力所需钢筋相叠加;其箍筋截面面积应由抗剪承载力和抗扭承载力所需钢筋相叠加。