8正反比例的意义比较[1]

比例的意义性质和正反比例比例是指两个或多个量之间的关系，它们之间存在倍数关系。

比例具有广泛的应用，能够帮助我们理解和解决各种实际问题。

1.描述事物的量与数值关系：比例能够描述两个或多个事物之间的数量关系，通过比例可以清晰地了解它们的数量差异和相对大小。

2.便于比较和分析：比例可以将不同事物之间的数量关系转化为一个统一的比较标准，方便进行比较和分析。

3.预测和推测：通过已知的比例关系，可以预测或推测未知量的数值，比例可以提供一种有效的量化推测方法。

比例的性质：1.传递性：如果两个比例相等，那么它们的对应项也相等。

例如，如果a:b=c:d，且b:c=e:f，则根据传递性可得a:d=e:f。

2.反比例的倒数性质：如果两个量成反比例关系，那么它们的倒数也成反比例关系。

例如，如果a:b=c:d，则根据反比例的倒数性质可得1/a:1/b=1/c:1/d。

3.乘法性质：如果两个比例的对应项分别相等，那么它们的乘积也相等。

例如，如果a:b=c:d，且b:c=e:f，则根据乘法性质可得(a/b)×(b/c)=(c/d)×(e/f)。

正比例：正比例是指两个量之间的关系是正相关的，即随着一个量的增大，另一个量也相应地增大。

正比例可以用一个常数来表示，该常数称为比例系数。

正比例关系可以表示为a=k×b，其中a和b是两个量，k是比例系数。

例如，如果速度和时间成正比例关系，则速度的变化与时间的变化是成比例的。

反比例：反比例是指两个量之间的关系是反相关的，即随着一个量的增大，另一个量相应地减小。

反比例关系可以用一个常数来表示，该常数称为比例常数。

反比例关系可以表示为a=k/b，其中a和b是两个量，k是比例常数。

例如，如果光的强度和距离成反比例关系，则光的强度的变化与距离的变化是成反比的。

正比例和反比例的区别在于它们表示的数量关系不同。

正比例关系表示随着一个量的增大，另一个量也增大；而反比例关系表示随着一个量的增大，另一个量减小。

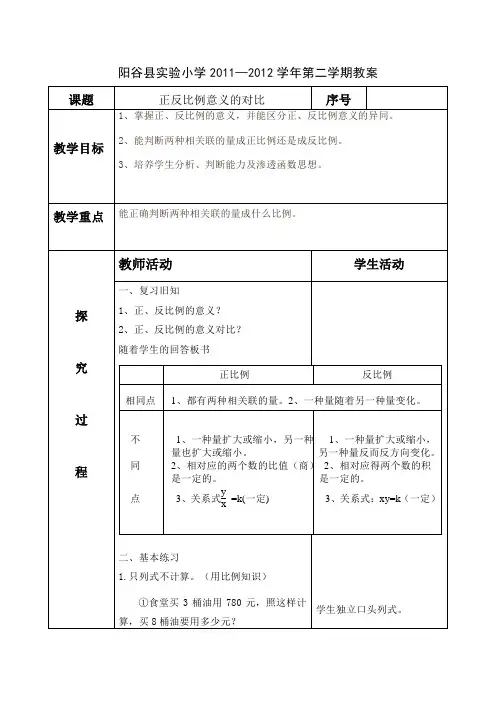
正比例和反比例的意义答案知识梳理教学重、难点作业完成情况典题探究例1．a与b是两种相关联的量，如果ab=1﹣ab，那么a与b成反比例．正确．考点：正比例和反比例的意义．分析：要想判定a和b成什么比例关系，必须根据式子，进行推导．根据正反比例的意义，分析数量关系，找出一定的量，然后看那两个变量是比值一定还是乘积一定，从而判定成什么比例关系．解答：解：因为ab=1﹣ab，所以2ab=1，ab=0.5（一定），可以看出，a与b是两种相关联的量，a随b的变化而变化，0.5是一定的，也就是a与b相对应的数的乘积一定，所以a与b是成反比例关系．故答案为：正确．点评：此题重点考查正比例和反比例的意义．例2．a÷b=c，当c一定时a和b正比例；当a一定时b和c反比例；当b一定时a 和c正比例．考点：正比例和反比例的意义．分析：依据正、反比例的意义，即若两个量的商一定，则这两个量成正比例，若两个量的乘积一定，则这两个量成反比例，即可进行解答．解答：解：（1）因为a÷b=c（一定），则a和b成正比例；（2）因为a÷b=c可得：bc=a（一定），则b和c成反比例；（3）因为a÷b=c可得：a÷c=b（一定），则a和c成正比例．故答案为：正比例、反比例、正比例．点评：此题主要考查正、反比例的意义，关键是看两个变量的商或乘积是否一定．例3．正方形的面积与边长不成比例．正确．（判断对错）考点：正比例和反比例的意义．分析：根据正比例和反比例的意义，在成比例的数量关系中，都有一个一定的量，两个变化的量，如果三个量都是变化的，那么就不成比例关系．解答：解：正方形的面积=边长×边长，当正方形的边长发生变化时，它的另一条边也随着变化，面积也同时发生变化，这三个量都是变化的，所以正方形的面积与边长不成比例．故答案为：正确．点评：此题重点考查正比例和反比例的意义．例4．圆锥体的高一定，底面积与体积成正比例．正确．考点：正比例和反比例的意义．专题：压轴题．分析：根据正反比例的意义，分析数量关系，找出一定的量（h），然后看那两个变量（底面积与体积）是比值一定还是乘积一定，从而判定是不是正比例关系．解答：解：因为圆锥的体积v=sh所以v：s=h（一定）可以看出，圆锥的底面积与体积是两种相关联的量，体积随底面积的变化而变化，圆锥体的高一定，高的三分之一也是一定的，也就是圆锥的体积与底面积的比值一定，所以圆锥的体积与底面积是成正比例关系．故答案为：正确．点评：此题重点考查正比例和反比例的意义．演练方阵A档（巩固专练）一．选择题（共15小题）1．（2011•赛罕区）长方体体积一定，底面积和高（）A．成正比例B．成反比例C．不成比例考点：正比例和反比例的意义．专题：压轴题．分析：根据正反比例的意义，分析数量关系，找出一定的量，然后看那两个变量是比值一定还是乘积一定，从而判定成什么比例关系．解答：解：长方体的底面积×高=长方体的体积（一定），可以看出，长方体的底面积和高是两种相关联的量，长方体的底面积随高的变化而变化，长方体的体积一定，也就是长方体的底面积和高的乘积一定，所以长方体的底面积和高是成反比例关系．故选：B．点评：此题重点考查正比例和反比例的意义．2．（2012•道真县）下列各题中，成反比例关系的是（）A．每公顷的产量一定，总产量和种的公顷数B．一根绳子，剪去的一段和剩下的一段C．平行四边形的面积一定，底和高考点：正比例和反比例的意义．分析：判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例；如果不是乘积或比值一定，就不成比例．解答：解：A、总产量÷公顷数=每公顷的产量（一定），是比值一定，所以成正比例；B、减去的一段+剩下的一段=绳子的总长（一定），是和一定，不是乘积或比值一定，所以不成比例；C、平行四边形的底×高=面积（一定），是乘积一定，所以成反比例；故选C．点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．3．（2012•广汉市模拟）分母一定，分子和分数值（）A．成正比例B．成反比例C．不成比例D．以上都不对考点：正比例和反比例的意义．分析：根据正反比例的意义和分子、分母、分数值之间的关系，找出一定的量（分母），然后看那两个变量（分子和分数值）是比值一定还是乘积一定，从而判定成什么比例关系．解答：解：因为分子：分母=分数值，所以分子：分数值=分母（一定），可以看出，分子与分数值是两种相关联的量，分子随分数值的变化而变化，分母是一定的，也就是分子与分数值相对应数的比值一定，所以分子与分数值成正比例关系．故选：A．点评：此题重点考查用正比例和反比例的意义辨识成正比例和反比例的量．4．（2013•永昌县）小明从家里去学校，所需时间与所行速度（）A．成正比例B．成反比例C．不成比例D．以上都不对考点：正比例和反比例的意义．专题：压轴题．分析：判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例．解答：解：所行速度×所需时间=家到学校的距离（一定），是乘积一定，所以所需时间与所行速度成反比例；故选B．点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．5．（2011•清原县）圆柱的体积一定，底面积和高（）A．成正比例B．成反比例C．不成比例考点：正比例和反比例的意义．分析：判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例．解答：解：圆柱的底面积×高=体积（一定），是乘积一定，所以圆柱的底面积和高成反比例；故选B．点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．6．（2012•北京）成反比例的两个量在变化时的规律是它们的（）不变．A．积B．商C．和考点：正比例和反比例的意义．专题：比和比例．分析：根据成反比例的意义可得，成反比例的两个量在变化时的规律是它们的积不变，由此即可选择正确答案．解答：解：根据反比例的意义可知，成反比例的两个量在变化时的规律是它们的积不变，故选：A．点评：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的乘积一定，这两种就叫做成反比例的量，它们的关系就是反比例关系．7．（2012•广汉市模拟）表示x和y成正比例关系的式子是（）A．x+y=6 B．y=x×C．x y=7考点：正比例和反比例的意义．分析：x和y成正比例关系，就说明x和y中相对应的两个数是对应的比值一定，如果是比值一定，x和y就成正比例，否则，x和y就不成正比例关系；据此进行逐项分析再选择．解答：解：A、x+y=6，是对应的“和”一定，所以x和y不成正比例；B、由y=x×，可得y：x=（一定），是对应的“比值”一定，所以x和y成正比例；C、xy=7（一定），是对应的“积”一定，所以x和y成反比例；故选：B．点评：此题属于根据正、反比例的意义，辨识两种相关联的量是否成正比例，就看这两种量是否是对应的比值一定，再做出判断．8．（2012•天柱县）正方形的周长和它的边长（）A．成正比例B．成反比例C．不成比例考点：正比例和反比例的意义．专题：压轴题．分析：判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例．解答：解：正方形的周长÷边长=4（一定），是比值一定，所以正方形的周长和它的边长成正比例；故选A．点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．9．（2012•龙海市）如果ab=3，那么a与b（）A．不成比例B．成反比例C．成正比例考点：正比例和反比例的意义．专题：压轴题；比和比例．分析：判断两种相关联的量成不成比例，成什么比例，就看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定，就成正比例，如果是乘积一定，就成反比例，如果是其它的量一定或乘积、比值不一定，就不成比例．解答：解：因为ab=3（值一定），则a和b成反比例；故选：B．点评：此题属于根据正、反比例的意义，辨识两种相关联的量成不成比例，成什么比例，就看这两种量是对应的比值一定，还是对应的乘积一定，还是对应的其它量一定，再做出判断．10．（2012•宝应县模拟）两个变量X和Y，当X•Y=45时，X和Y是（）A．成正比例量B．成反比例量C．不成比例量考点：正比例和反比例的意义．分析：根据正反比例的意义，分析x与y之间的数量关系，找出一定的量，然后看x与y两个变量是比值一定还是乘积一定，从而判定成什么比例关系．解答：解：X•Y=45（一定），可以看出，X和Y是两种相关联的量，X随Y的变化而变化，45是一定的，也就是X与Y相对应数的乘积一定，所以X与Y成反比例关系．故选：B．点评：此题重点考查正比例和反比例的意义．11．（2012•金沙县）下列a和b成反比例关系的是（）A．b=3+a B．a+b= C．a= D．3：a=b：2考点：正比例和反比例的意义．分析：只要把原来的式子进行整理、变形，看a和b是乘积一定，还是比值一定，如果乘积一定，则两种量成反比例；如果比值一定，则两种量则成正比例，进而选择即可．解答：解：A，b=3+a，所以b﹣a=3，是a、b的差一定，所以a、b不成比例；B，a+b=，是a、b的和一定，所以a、b不成比例；C，a=中，没有相关联的两个量，不成比例；D，3：a=b：2，所以ab=6（一定），是a与b的乘积一定，所以是a、b成反比例；故选：D．点评：此题考查了判断成正、反比例的方法：看两个相关联的量的乘积一定还是比值一定，如果乘积一定，则两种量成反比例；如果比值一定，则两种量则成正比例．12．（2012•长寿区）已知=，那么x与y（）A．成正比例B．不成比例C．成反比例考点：正比例和反比例的意义．专题：综合判断题．分析：根据正、反比例的意义，如果x：y=k（一定），那么x和y就成正比例；如果xy=k （一定），那么x和y就成反比例．先根据比例的基本性质改写后，即可知答案．解答：解：由= 得出：xy=5×8=40，符合反比例关系式，所以x和y成反比例．故选：C．点评：此题主要考查正、反比例的意义及比例的基本性质．13．（2013•华亭县模拟）表示x和y成正比例关系的式子是（）A．x+y=6 B．x﹣y=8 C．y=5x D．x y=7考点：正比例和反比例的意义．分析：判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例；如果不是比值或乘积一定，就不成比例．解答：解：A、x+y=6，是和一定，不成比例；B、x﹣y=8，是差一定，不成比例；C、因为y=5x，y÷x=5，是比值一定，所以成正比例；D、x×y=7，是乘积一定，所以成反比例；故选C．点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．14．（2014•广州模拟）长方形的面积一定，长和宽（）A．成正比例B．成反比例C．不成比例考点：正比例和反比例的意义；长方形、正方形的面积．分析：根据正比例的意义x：y=k（一定）和反比例的意义xy=k（一定），因为长×宽=长方形的面积（一定），符合反比例的意义．解答：解：根据长方形的面积公式，长×宽=长方形的面积（一定），符合反比例的意义xy=k （一定），所以长方形的面积一定，长和宽成反比例．故选B．点评：此题主要考查正、反比例的意义，以及长方形的面积公式．15．（2012•富源县）下列X和Y成反比例关系的是（）A．Y=3+X B．X+Y= C．X=Y D．Y=考点：正比例和反比例的意义．专题：常规题型．分析：判断两种相关联的量是否成反比例，就看这两种量是否是对应的乘积一定，如果是乘积一定，就成反比例，如果不是乘积一定或乘积不一定，就不成反比例．据此进行判断并选择．解答：解：A、因为Y=3+X，所以Y﹣X=3（一定），是X和Y的差一定，X和Y不成比例；B、因为X+Y=（一定），是X和Y的和一定，X和Y不成比例；C、因为X=Y，所以X÷Y=（一定），是比值一定，X和Y成正比例；D、因为Y=，所以XY=1，是乘积一定，X和Y成反比例；故选：D．点评：此题属于根据正、反比例的意义，辨识两种相关联的量是否成反比例，就看这两种量是否是对应的乘积一定，再做出选择．二．填空题（共13小题）16．（2010•保靖县）正方体的一个面的面积和它的表面积成正比例．考点：正比例和反比例的意义．分析：判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例．解答：解：正方体的表面积÷一个面的面积=6（一定），是比值一定，所以正方体的一个面的面积和它的表面积成正比例；故答案为：正．点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．17．（2011•重庆）陈思思参加100米短跑，她跑步的速度与时间成反比例．考点：正比例和反比例的意义．分析：判断速度与时间成什么比例，要看速度与时间是比值一定，还是乘积一定，若比值一定，成正比例，乘积一定，成反比例．解答：解：因为速度×时间=100米，是乘积一定，所以跑步的速度与时间成反比例．故答案为：反．点评：本题考查对正、反比例的判断，看两种量是对应的比值一定，还是对应的乘积一定，再做出判断．18．（2011•永春县模拟）y=x（x≠0），x和y成正比例．正确．考点：正比例和反比例的意义．分析：要想判定x和y成不成正比例关系，必须根据式子，进行推导．再根据正比例的意义，分析数量关系，找出一定的量，看看x和y是不是比值一定．解答：解：因为y=x（x≠0），所以y：x=（一定），可以看出，y和x是两个相关联的变化的量，它们相对应的数的比值是，是一定的，．所以y和x成正比例关系．故答案为：正确．点评：此题重点考查正比例的意义．19．（2012•广州一模）人的身高和体重成正比例．×．（判断对错）考点：正比例和反比例的意义．分析：判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例；如果不是乘积或比值一定，就不成比例．解答：解：人的身高和体重虽是两种相关联的量，但是它们的乘积或比值都不一定，所以不成比例；故答案为：×．点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．20．（2012•安岳县模拟）汽车行驶的路程和时间成正比例．正确．（判断对错）考点：正比例和反比例的意义．分析：判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例．解答：解：汽车行驶的路程÷时间=速度（一定），是比值一定，所以汽车行驶的路程和时间成正比例；故答案为：正确．点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．21．（2012•陆良县模拟）速度一定，时间和路程成正比例正确．（判断对错）考点：正比例和反比例的意义．分析：判断时间和路程是否比例，就看这两种量是否是对应的比值一定，还是乘积一定，如果是比值一定，就成正比例，如果乘积一定，就成反比例．解答：解：路程÷时间=速度（一定），是比值一定，时间和路程成正比例．故答案为：正确．点评：此题属于辨识成正比例的量，就看这两种量是否是对应的比值一定，再做出判断．22．（2012•沛县模拟）y=5x，x和y成反比例．错误．考点：正比例和反比例的意义．分析：判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例．解答：解：因为y=5x，所以y：x=5（一定），是比值一定，所以成正比例；故答案为：错误．点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．23．（2012•广州模拟）圆周率一定，圆的周长和它的直径成正比例．考点：正比例和反比例的意义；圆、圆环的周长．分析：判定两种量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定，就成反比例．解答：解：圆的周长÷直径=圆周率（一定），是比值一定，所以圆的周长和它的直径成正比例；故答案为：正．点评：此题属于根据正、反比例的意义，判断两种相关联的成正比例还是成反比例，就看是对应的比值一定，还是对应的乘积一定，再做出选择．24．（2012•道真县）已知4X=3Y，（X、Y不为0）那么X：Y=（3：4），X和Y 成正比例．考点：正比例和反比例的意义．分析：先根据比例的性质把4和X看做比例的两个外项，把3和Y看做比例的两个内项，改写成比例式为X：Y=3：4，3：4可改写成，所以这两种量是对应的比值一定，X 和Y就成正比例．解答：解：因为4X=3Y，所以X：Y=3：4，X：Y=（一定），是比值一定，所以成正比例；故答案为：3：4，正．点评：此题属于考查对比例的基本性质的运用和根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例的题目．25．（2012•团风县模拟）工作时间一定，工作效率和工作总量成正比例．考点：正比例和反比例的意义．分析：判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例．解答：解：工作总量÷工作效率=工作时间（一定），是比值一定，所以工作效率和工作总量成正比例；故答案为：正．点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．26．（2013•延边州）圆锥的底面积一定，高和体积成正比例．正确．（判断对错）考点：正比例和反比例的意义；圆锥的体积．分析：判断圆锥的高和体积是否成正比例，就看它们是不是比值一定，若比值一定，则成，否则，就不成．解答：解：圆锥的体积÷高=底面积（一定），是比值一定，因此成正比例．故判断为：正确．点评：本题考查对正比例的判断，就看两种量是不是对应的比值一定，再做出判断．27．（2014•慈利县）小新跳高的高度和身高不成比例．√．考点：正比例和反比例的意义．分析：判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例；如果比值或乘积不一定，就不成比例．解答：解：小新跳高的高度和身高这两种相关联的量，它们的比值或乘积都不一定，所以不成比例；故答案为：√．点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．28．（2014•海安县模拟）如果=，x 和y成反比例；如果14x=y，x和y成正比例．考点：正比例和反比例的意义．分析：先根据比例的性质改写成比例或两内项积等于两外项积的形式，再判定两种相关联的量成正或反比例，如果是比值一定就成正比例；如果是乘积一定就成反比例．解答：解：因为=，所以x×y=4（一定），是乘积一定，所以x和y成反比例；因为14x=y，所以y：x=14（一定），是比值一定，所以x和y成正比例；故答案为：反，正．点评：此题属于根据比例的基本性质和正、反比例的意义，判断两种相关联的量是成正比例还是成反比例的．B档（提升精练）一．选择题（共15小题）1．（2012•陕西）正方形的面积和边长（）A．成正比例B．成反比例C．不成比例考点：正比例和反比例的意义．分析：判定两种量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定，就成反比例．解答：解：正方形的面积÷边长=边长（不一定），比值不一定，所以正方形的面积和边长不成比例；故选C．点评：此题属于根据正、反比例的意义，判断两种相关联的成正比例还是成反比例，就看是对应的比值一定，还是对应的乘积一定，再做出解答．2．（2012•武定县模拟）买同样的书，花钱的总价与（）成正比例．A．书的本数B．书的页数C．书的单价D．不能确定考点：正比例和反比例的意义．分析：根据总价=单价×数量的数量关系进行分析．要想知道总价与什么成正比例，就要找到一定的量和变化的量，根据正比例的意义，总价与变量相比才能成正比例．解答：解：买同样的书，也就是书的单价一定．可得：总价：数量=单价（一定）可以看出，总价和数量是两种相关联的量，总价随数量的变化而变化．单价一定，也就是总价与数量相对应数的比值一定．所以花钱的总价与数量（书的本数）成正比例关系．故选：A．点评：此题重点考查正比例和反比例的意义．3．（2012•中山模拟）下列关系式中x、y 都不为0，则x与y不是成反比例关系的是（）A．x= B．y=3÷x C．x=×πD．x=考点：正比例和反比例的意义．分析：判断x和y是否成反比例，就看x和y是否是对应的乘积一定，如果是乘积一定，就成反比例，如果不是乘积一定或乘积不一定，就不成反比例．据此进行逐项分析后再作出选择．解答：解：A、因为x=，则有xy=4（一定），所以x和y成反比例；B、因为y=3÷x，则有xy=3（一定），所以x和y成反比例；C、因为x=×π，则有xy=π（一定），所以x和y成反比例；D、因为x=，则有=4（一定），所以x和y成正比例；故选：D．点评：此题属于根据反比例的意义，辨识两种相关联的量是否成反比例，就看这两种量是否是对应的乘积一定，再做出判断．4．（2012•商丘模拟）7x=5y，（x、y都不等于零），那么x和y（）A．成正比例B．成反比例C．不成比例考点：正比例和反比例的意义．。

正比例和反比例的意义知识点一：正比例和反比例的意义（1）正比例两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值（也就是商）一定，这两种量变叫做成正比例的量，它们的关系叫做正比例关系。

用字母x 和y 表示两种相关联的量，用k 表示一定的量，那么正比例关系可以写成：()一定k xy = 例如，总价随着数量的变化而变化，总价和数量的比的比值（单价）是一定的，我们就说，总价和数量是成正比例的量。

工总工时＝工效（一定） 工总和工时是成正比例的量 路程时间 ＝速度（一定） 所以路程与时间成正比例。

（2）反比例两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系。

用字母x 和y 表示两种相关联的量，用k 表示一定的量，那么反比例关系可以写成：x ×y =k （一定）例如，长×宽＝面积（一定） 长和宽是成反比例的量每本的页数×装订的本数＝纸的总页数（一定） 每本的页数和装订的本数是成反比例的量知识点二：正比例和反比例有什么相同点和不同点？（1）相同点：正、反比例都是研究两种相关联的量之间的关系，即一种量变化，另一种量也随着变化。

（2）不同点：正比例是两种相关联的量中相对应的两个数的比值（商）一定；反比例是两种相关联的量中相对应的两个数的积一定。

正比例反比例相同点不同点知识点三：正比例和反比例的图像是一条什么线？（1）正比例关系的图象是一条过原点的直线。

（2）反比例关系的量是一条不过原点的曲线。

知识点四：正比例和反比例的判断（1）先判断两种量x 和y 是不是相关联的量，即一种量变化，另一种量也随着变化。

（2）若符合()一定k xy =，则x 和y 成正比例；若符合x ×y =k （一定），则x 和y 成反比例；否则，这两种量就不成比例关系。

【典型例题】题型一：根据图标填写信息例1 ：购买面粉的重量和钱数如下表，根据表填空。

1、正比例的意义是：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

2、用字母表示：如果用字母x和y表示两种相关联的量，用k表示它们的比值（一定），正比例关系可以用关系式表示：x÷y=k （一定）还可表示为：x=ky以上各种商都是一定的，那么被除数和除数．所表示的两种相关联的量，成正比例关系．注意：在判断两种相关联的量是否成正比例时,应注意已知的两种量必须是两种相关联的量（也就是有关系的两种量），有些量，虽然也是一种量随着另一种的变化而变化，但它们相对应的两个数的比值不一定，它们就不能成正比例．例如：一个人的年龄和它的体重，就不能成正比关系，正方形的边长和它的面积也不成正比例关系．行驶的路程和时间是成比例的量。

“正反比例”归纳：相同点：①正比例和反比例都含有三个数量，在这三个数量中，均有一个定量、两个变量。

②在正、反比例的两个变量中，均是一个量变化，另一个量也随之变化。

正比例中相关联的两种量的变化方向是一致的，即：同时扩大或同时缩小，关键是：相对应的两个数的“比值一定，也就是商一定”；反比例中两种量的变化方向是相反的，即：一个量扩大，则另一个量缩小，一个缩小，另一个量则扩大，关键是：相对应的两个数的“积一定”。

不同点：正比例的定量（即不变的量）是两个变量中相对应的两个数的比值。

反比例的定量（即不变的量）是两个变量中相对应的两个数的积。

②正比例的图像时上升直线；反比例是曲线。

③公式不同：正比例是（x y=k（一定）），反比例是（xy=k（一定））。

④规律不同：正比例是一个数缩小，另一个数也缩小，一个数扩大，另一个数也扩大；反比例是一个数缩小，另一个数就扩大，一个数扩大另一个数就缩小。

门诊医院：举例：当路程一定时，已行路程与未行路程成比例吗?为什么？分析：虽然这里的已行路程和未行路程也是相关联的两个量，但是它们的变化规律是增加或减少的数，换句话说已行路程与未行路程不是一个量随另一个量的扩大而扩大或缩小而缩小，也就是它们之间不能相乘，也不能相除，得不到一个积或一个商，所以它们不成比例。

正比例和反比例的意义知识点一：正比例和反比例的意义（1）正比例两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值（也就是商）一定，这两种量变叫做成正比例的量，它们的关系叫做正比例关系。

用字母x 和y 表示两种相关联的量，用k 表示一定的量，那么正比例关系可以写成：y=k (一定)x例如，总价随着数量的变化而变化，总价和数量的比的比值（单价）是一定的，我们就说，总价和数量是成正比例的量。

工总＝工效（一定）工总和工时是成正比例的量工时路程＝速度（一定）所以路程与时间成正比例。

时间（2）反比例两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系。

用字母x 和y 表示两种相关联的量，用k 表示一定的量，那么反比例关系可以写成：x × y = k （一定）例如，长×宽＝面积（一定）长和宽是成反比例的量每本的页数×装订的本数＝纸的总页数（一定）每本的页数和装订的本数是成反比例的量知识点二：正比例和反比例有什么相同点和不同点？（1）相同点：正、反比例都是研究两种相关联的量之间的关系，即一种量变化，另一种量也随着变化。

（2）不同点：正比例是两种相关联的量中相对应的两个数的比值（商）一定；反比例是两种相关联的量中相对应的两个数的积一定。

不同点知识点三：正比例和反比例的图像是一条什么线？（1）正比例关系的图象是一条过原点的直线。

（2）反比例关系的量是一条不过原点的曲线。

知识点四：正比例和反比例的判断（1）先判断两种量x 和y 是不是相关联的量，即一种量变化，另一种量也随着变化。

（2）若符合y=k (一定)，则x 和y 成正比例；若符合x ×y =k （一定），则x 和y 成反x比例；否则，这两种量就不成比例关系。

【典型例题】题型一：根据图标填写信息例 1 ：购买面粉的重量和钱数如下表，根据表填空。

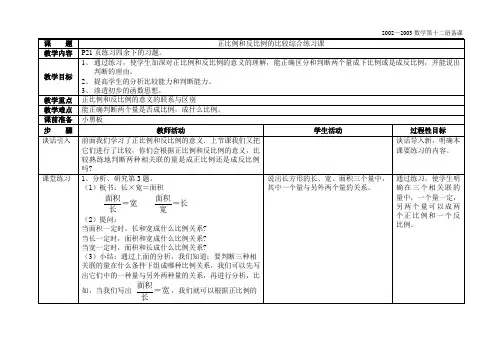
正比例：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，它们的关系叫做成正比例关系．正方形的周长与边长圆的周长与直径路程比时间等于速度(一定)反比例：两种相关联的量，一种量变化，另一种量也随着变化，这两种量中相对应的两个数的积一定。

这两种量叫做成反比例的量。

它们的关系叫做反比例关系。

用x×y=k(一定）来表示。

1.百米赛跑，路程100米不变，速度和时间是反比例；2.排队做操，总人数不变，排队的行数和每行的人数是反比例；3.做纸盒子，总个数一定，每人做的个数和人数成反比例；4.买东西（实际就用文具用品），总钱数一定，它的单价和数量是反比例；5.长方形的面积一定，长和宽是反比例；6.长方体的体积一定，底面积和高是反比例。

7.等分一块蛋糕，每人分到的蛋糕与人数成反比例。

8.总价一定,单价与数量成反比例.9.长方体体积一定,底面积与高成反比例10.总纸盒一定,每人做的个数与人数成反比例反比例的意义形如y=k;x*y=k乘1/x（k不等于0）的函数叫做反比例函数，k叫做反比例系数。

y*x=k(一定)，这是求反比例的公式。

编辑本段反比例的实质两种相关联的量，一种量变化，另一种量也随着变化，这两种量中相对应的两个数的积一定。

这两种量叫做成反比例的量。

它们的关系叫做反比例关系。

用xy=k(一定）k不等于0来表示。

简单点来说，就是如果一样事物增加了，另一样事物减少，它减少了，另一样事物增加，这两个事物的关系就叫做反比例关系。

编辑本段正比例和反比例之间的相互转化当正比例中的x值（自变量的值），转化为它的倒数时，由正比例转化为反比例；当反比例中的x值（自变量的值）也转化为它的倒数时，由反比例转化为正比例。

编辑本段生活中的反比例1.百米赛跑，路程100米不变，速度和时间成反比例（即路程一定，速度和时间成反比例）；2.排队做操，总人数不变，排队的行数和每行的人数成反比例；3.做纸盒子，总个数一定，每人做的个数和人数成反比例；4.买东西（实际就用文具用品），总价一定，它的单价和数量是反比例；5.长方形的面积一定，长和宽是反比例（提示：但是长方形的周长与长宽不成比例【既不成正比例也不成反比例】）；6.长方体的体积一定，底面积和高是反比例。

课时计划第周第课（章、单元）第节第26课时年月日课题正、反比例意义的联系与区别课型教学三维目标知识与能力通过比较，使学生进一步理解正比例和反比例的意义，弄清它们的联系和区别，掌握它们的变化规律，能够正确地判断正、反比例的关系，过程与方法使学生进一步理解正比例和反比例的意义情感态度与价值观进一步发展学生的分析，比较等能力。

教材分析重点正确判断正、反比例的关系难点：区别正、反比例教法掌握正、反比例的特征学法练习法教具投影教学过程：一、复习1、判断下面每题中的两种量是成正比例还是成反比例？（1）速度一定，路程和时间（2）正方形的边长和它的面积（3）生产总时间一定，生产一个零件所用的时间和零件总数（4）中国儿童报的订烽和钱数（5）圆的面积与半径6、长方形的周长和宽二、指导练习1、出示表一：路程40 80 160 200 320时间 1 2 4 5 82、出示表二：速度120 90 60 40 30时间 3 4 6 9 12说一说：从表一中你怎样发现速度是一定的？根据什么判断路程和时间成正比例？想一想：路程、速度和时间这三个量中每两个量之间有什么样的比例关系？3、小结：判断两种量是否成比例，成什么比例，方法是什么？想一想：路程、速度和时间这三个量中每两个量之间的什么样的比例关系？板书：速度×时间=路程路程/时间=速度路程/速度=时间师：当速度一定时，路程和时间成什么比例关系？当路程一定时，速度和时间成什么比例关系？当时间一定时，路程和速度成什么比例关系？4、比较正比例和反比例关系。

通过前面的例子，比较正比例关系和反比例关系。

你能写出它们的相同点和不同点吗？板书：相同点：都有两种相关联的量，一种量变化，另一种量也随着变化。

不同点：正比例：两种量中相对应的两个数的比值（商）一定。

关系式y/x=k (一定）板书设计：速度×时间=路程路程/时间=速度路程/速度=时间作业布置：选用课时作业教学后记：。

周测培优卷8正、反比例的意义和判定一、我会填。

(每空2分，共40分)1. 已知x、y是两种相关联的量，k是一个固定的且不为0的数。

(1)当x k ＝y时，x和y成()比例。

(2)当xy＝k时，x和y成()比例。

2. 正比例与反比例的不同点：成正比例的两种量中，相对应的两个数的()一定，成反比例的两个量中，相对应的两个数的()一定。

3. 两种相关联的量，一种量扩大到原来的3倍，另一种量也随着扩大到原来的3倍，这两种量成()比例。

5. 根据花生的千克数、花生油的千克数和出油率这三个量的关系填空。

(1)如果花生的千克数一定，花生油的千克数和出油率成()比例。

(2)如果花生油的千克数一定，花生的千克数和出油率成()比例。

(3)如果出油率一定，花生的千克数和花生油的千克数成()比例。

6. 小林骑自行车从家到学校，他骑车的速度和所需时间成()比例。

7. 在A×B＝C(A，B，C均不为0)中，当B一定时，A和C成()比例，当C 一定时，A 和B 成( ) 比例。

①不成比例 ②成正比例 ③成反比例(1)一批纸的张数一定，每本练习本的张数和装订的本数。

( ) (2)圆的半径和它的面积。

( )(3)行一段路程，已行的路程和剩下的路程。

( )(4)生产零件的总时间一定，生产一个零件的时间与生产零件的总个数。

( )(5)小丽从家到学校，步行的速度和所需时间。

( )9. 如果m 3 ＝ 3n ，那么m 和n 成( )比例；如果5m ＝n ，那么m和n 成( )比例。

二、我会判。

(对的在括号里打“√”，错的打“×”。

每题2分，共10分) 1. 平行四边形的面积一定，它的底与高成反比例。

( )2. 两种相关联的量，不成正比例就成反比例。

( )3. 订阅《少年文艺》的份数与总钱数成反比例。

( )4. 长方体的底面积一定，高和体积成反比例。

( )5. 图上距离一定，实际距离和比例尺成正比例。

( ) 三、我会选。

正反比例的意义学习专用正比例和反比例是数学中常见的关系类型，它们在我们的日常生活中也得到了广泛的应用。

正比例关系表示两个变量之间的变化方向相同，而反比例关系表示两个变量之间的变化方向相反。

以下将从几个方面探讨正、反比例的意义和应用。

一、正比例的意义及应用正比例关系在现实生活中有很多重要的应用。

举例来说，我们知道速度等于路程除以时间，当路程和时间之间存在正比例关系时，我们可以利用速度的概念来计算物体的运动情况。

在工程学中，正比例关系也有广泛的应用，例如材料的拉伸和弹性参数之间往往存在正比例关系，这些关系可以帮助我们设计更好的材料和结构。

此外，正比例关系还可以帮助我们解决很多现实生活中的实际问题。

以购买商品为例，价格和数量之间往往存在正比例关系。

当我们知道商品的单价时，我们就可以根据价格和数量之间的正比例关系计算出购买该商品所需的总价格。

在经济学中，正比例关系也有很多应用，例如劳动力和产出之间的关系，税率和收入之间的关系等。

二、反比例的意义及应用反比例关系同样在现实生活中有着重要的应用。

举例来说，我们知道速度是一定时间内所走路程的倒数，当路程和时间之间存在反比例关系时，我们可以利用速度的概念来计算物体的运动情况。

在物理学中，反比例关系也有广泛的应用，例如电压和电流之间的关系，电阻和电流之间的关系等。

反比例关系还可以帮助我们解决很多实际问题。

以工作时间为例，当几个人一起工作时，他们的工作效率与工作时间之间往往存在反比例关系。

当我们知道几个人一起工作所需的总时间时，我们就可以根据工作效率和工作时间之间的反比例关系计算出每个人的工作时间。

在金融学中，反比例关系也有很多应用，例如利率和贷款金额之间的关系，需求量和价格之间的关系等。

综上所述，正比例和反比例关系在数学中与现实生活中都有着重要的意义和应用。

正比例关系帮助我们计算物体运动、设计材料和解决实际问题；反比例关系帮助我们计算物体运动、解决实际问题和理解一些经济学和金融学的概念。