(完整版)三角函数求值问题

【题目】：求解三角函数计算问题我们面临一个关于三角函数的计算问题，需要求出一些数值。

这个问题涉及到两个角度（α和β）和对应的正弦、余弦和正切值。

我们将在下面提供详细的题目和解答过程。

题目：求以下三角函数值的计算公式：sin(α) = 0.345, cos(α) = 0.657, tan(α) = 2.345已知：我们需要求解的三角函数值是：sin(β) = ?cos(β) = ?tan(β) = ?解答过程：首先，根据三角函数的定义，我们知道sin(α) = 0.345，cos(α) = 0.657，tan(α) = 2.345。

这些是我们所知道的值。

接下来，我们可以通过三角函数的公式来求解sin(β)，cos(β)，tan(β)。

这些公式包括：sin(β) = sin(α)cos(β-α)，cos(β) = cos(α)cos(β+α)，tan(β) = tan(α)cot(β-α)。

我们需要对每一个公式进行详细的推导。

对于第一个公式，我们注意到sin(β) = sin(α)cos(β-α)。

首先，我们知道cos(β-α) = cos([α+(β-α)]) = cos(α)cos(β+α)。

结合这两个公式，我们可以得到：sin(β) = sin(α)cos(β+α)。

接下来，我们可以通过已知的cos(α) 和sin(α) 来求解sin(β)。

同理，对于第二个公式，我们可以通过已知的cos(α) 和cos(β+α) 来求解cos(β)。

对于第三个公式，我们需要将cot(β-α) 转换为tan(β)。

然后我们将这些值带入tan(β) 的公式中。

以下是详细的过程和答案：sin(β) = 0.345 * cos(β+α)，其中cos(β+α) 可以由cos([α+(β-α)]) 得到，结果为：sin(β) = 0.345 * (cos(α)cos(β+α)) = 0.345 * 0.657 * (cos(β))^2 - 0.345 * sin(β) * sin(β+π/2)。

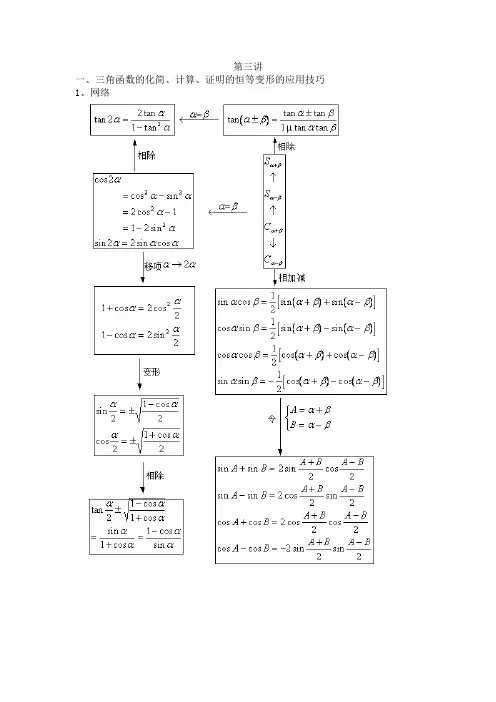
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结（1）变换函数名对于含同角的三角函数式，通常利用同角三角函数间的基本关系式及诱导公式，通过“切割化弦”，“切割互化”，“正余互化”等途径来减少或统一所需变换的式子中函数的种类，这就是变换函数名法．它实质上是“归一”思想，通过同一和化归以有利于问题的解决或发现解题途径。

【例1】已知θ同时满足和,且a、b 均不为0，求a、b的关系。

练习：已知sin（α＋β）＝，cos（α－β）＝，求的值。

2）变换角的形式对于含不同角的三角函数式，通常利用各种角之间的数值关系，将它们互相表示，改变原角的形式，从而运用有关的公式进行变形，这种方法主要是角的拆变．它应用广泛，方式灵活，如α可变为（α＋β）－β；2α可变为（α＋β）＋（α－β）；2α－β可变为（α－β）＋α；α／2可看作α／4的倍角；（45°＋α）可看成（90°＋2α）的半角等等。

【例2】求sin（θ＋75°）＋cos（θ＋45°）－cos（θ＋15°）的值。

练习已知，求的值【例3】已知sinα＝Ａsin（α＋β）（其中cosβ≠A），试证明：tan（α＋β）＝提示：sin[（α＋β）－β]＝Ａsin （α＋β）（3）以式代值利用特殊角的三角函数值以及含有1的三角公式，将原式中的1或其他特殊值用式子代换，往往有助于问题得到简便地解决。

这其中以“1”的变换为最常见且最灵活。

“1”可以看作是sin2x＋cos2x, sec2x－tan2x, csc2x －cot2x，tanxcotx, secxcosx, tan45°等，根据解题的需要，适时地将“1”作某种变形，常能获得较理想的解题方法。

【例4】化简：（4）和积互化积与和差的互化往往可以使问题得到解决，升幂和降次实际上就是和积互化的特殊情形。

这往往用到倍、半角公式。

（完整版）三角函数的运算经典习题以下是一些关于三角函数运算的经典题，希望能对大家的研究有所帮助。

题一：正弦函数的运算1. 求解 $\sin \left(x + \frac{\pi}{6}\right) = \frac{1}{2}$ 的解集。

2. 计算 $\sin \left(\frac{\pi}{3}\right) + \cos\left(\frac{\pi}{4}\right)$ 的值。

3. 简化表达式 $\sin \left(\frac{\pi}{2} - x\right)$。

4. 计算 $\sin \left(\frac{\pi}{6}\right) \cdot \cos\left(\frac{\pi}{4}\right)$ 的值。

题二：余弦函数的运算1. 求解 $\cos \left(2x - \frac{\pi}{3}\right) = 0$ 的解集。

2. 计算 $\cos \left(\frac{\pi}{6}\right) \cdot \cos\left(\frac{\pi}{3}\right)$ 的值。

3. 简化表达式 $\cos \left(\frac{\pi}{2} + x\right)$。

4. 计算 $\cos \left(\frac{3\pi}{4}\right) + \sin\left(\frac{\pi}{4}\right)$ 的值。

题三：正切函数的运算1. 求解 $\tan \left(\frac{x}{2}\right) = \sqrt{3}$ 的解集。

2. 计算 $\tan \left(\frac{\pi}{4}\right) \cdot \tan\left(\frac{\pi}{6}\right)$ 的值。

3. 简化表达式 $\tan \left(\frac{\pi}{2} - x\right)$。

4. 计算 $\tan \left(\frac{\pi}{3}\right) - \sin\left(\frac{\pi}{6}\right)$ 的值。

三角函数中的参数求值或求范围问题
1、等式恒成立型
这一类型包括奇偶性概率、周期性概念、存在性问题三种，解决方法有一般定义法或先用特值求解再进行证明两个思路。

例1、若是奇函数，求θ的值。

若是偶函数呢？
解法1：（定义法）因为是奇函数，所以对恒成立，即
恒成立，所以为所求。

解法2：（特值法）因为是奇函数，所以f(0)=0，得，故，此时，而
，故为所求。

解法3：因为是奇函数，所以对恒成立，即
恒成立，进而恒成立，所以，即为所求。

2、不等式恒成立型
这类问题的理论依据是：若将含参数t的关于x的不等式分离
，通过求g(x)的最值，再求t的取值范围。

（1）；
（2）。

例2、已知函数
恒成立，求实数a的范围。

解析：
，由，由对。

3、函数最值型
此类问题主要是分离变量转换为求函数值域或者转换为二次函数分类讨论求最值。

例3、若函数
的最小值是－6，求实数a的值。

解析：令。

（1）上递增，所以
，得a=－7。

（2）当时，g(t)在[－1，1]上递减，所以
，得a=7；
（3）当
时，g(t)在
递增。

所以，舍去；综上所述，得。

高考数学-三角函数专题复习三角函数专题考点例题解析】考点1.求值1、求sin330°、tan690°、sin585°的值。

解：利用三角函数的周期性和对称性，可得：sin330°=sin(360°-30°)=sin30°=1/2tan690°=tan(720°-30°)=tan30°=1/√3sin585°=sin(540°+45°)=sin45°=√2/22、已知角α为第三象限角，求sin(α+π/2)的值。

解：由于α为第三象限角，所以sinα<0，cosα<0.又因为sin(α+π/2)=cosα，所以sin(α+π/2)<0.3、已知sinθ+cosθ=5/3，cosθ-sinθ=2，求sin2θ的值。

解：将sinθ+cosθ和cosθ-sinθ相加，可得cosθ+cosθ=5/3+2=11/3，即cosθ=11/6.将cosθ-sinθ和sinθ+cosθ相减，可得2sinθ=-1/6，即sinθ=-1/12.代入sin2θ=2sinθcosθ的公式，可得sin2θ=-11/72.4、已知si n(π/4-α)=2/√5，求cosα的值。

解：sin(π/4-α)=sinπ/4cosα-cosπ/4sinα=2/√5，代入cosπ/4=√2/2和sinπ/4=√2/2，可得cosα=1/√10.5、已知f(cosx)=cos3x，求f(sin30°)的值。

解：将x=π/6代入f(cosx)=cos3x，可得f(cosπ/6)=cos(3π/6)=cosπ=-1.又因为sin30°=cosπ/6，所以f(sin30°)=-1.6、已知tanα=15π/22，求cos(π/2-α)的值。

解：tanα=15π/22，所以α为第三象限角，cos(π/2-α)=sinα>0.由tanα=sinα/cosα，可得cosα=15/√466，代入sin^2α+cos^2α=1，可得sinα=7/√466，最终可得cos(π/2-α)=7/15.7、已知tan(π/4+x)=2tan(π/4-x)，求cos2x的值。

高考数学三角函数求值历年真题精讲2024一、简介高考数学中，三角函数求值是一个重要的考点，也是学生容易出错的地方。

本文将通过精讲2024年历年真题，详细介绍三角函数求值的方法和技巧。

二、问题一2024年高考数学真题中的第一道三角函数求值题目如下：已知角A的终边经过点P(-3,4)，且在第二象限，求sinA和tanA 的值（结果保留两位小数）。

解析：首先根据点P的坐标(-3,4)在第二象限，可以得知该角的终边位于单位圆上，并且与x轴的夹角为A。

其次，根据sinA的定义，sinA = y/r = 4/5 = 0.80。

最后，根据tanA的定义，tanA = y/x = 4/-3 ≈ -1.33。

三、问题二2024年高考数学真题中的第二道三角函数求值题目如下：已知cosA = -1/3，且角A的终边经过点Q，求点Q的坐标。

解析：根据cosA的定义，cosA = x/r，代入已知条件可得-1/3 = x/r。

由于终边经过点Q，所以终边与x轴的夹角A为180°，即角A 是反余弦函数的特解。

通过求解反余弦函数可得，A = arccos(-1/3) ≈ 109.47°。

根据单位圆的性质，r = 3，所以可以得到坐标点Q(x,y) = (3cosA, 3sinA) ≈ (-1, √8)。

四、问题三2024年高考数学真题中的第三道三角函数求值题目如下：已知sinB = 3/5，且角B的终边经过点R，求点R的坐标。

解析：根据sinB的定义，sinB = y/r，代入已知条件可得3/5 = y/r。

由于终边经过点R，所以终边与x轴的夹角B为逆时针方向的特解。

通过求解反正弦函数可得，B = arcsin(3/5) ≈ 36.87°。

根据单位圆的性质，r = 5，所以可以得到坐标点R(x,y) = (5cosB, 5sinB) ≈ (4, 3)。

五、问题四2024年高考数学真题中的第四道三角函数求值题目如下：已知tanC = -√3，且角C的终边经过点S，求点S的坐标。

(完整版)高考三角函数经典解答题及答案1. 在△ABC 中，角 A、B、C 所对的边分别是 a、b、c，且 a²+c²-b²=(1) 求 sin²(2A+C)+cos²B 的值；(2) 若 b=2，求△ABC 面积的最大值。

解：(1) 由余弦定理：cosB=(a²+ c²- b²)/(2ac)=4/√115，得sinB=√(1-cos²B)=3√(23)/23。

由正弦定理sin²(2A+C)+cos²B=4sin²B+cos²B=13/23。

2. 在△ABC 中，角 A、B、C 的对边分别为 a、b、c，且bcosC=3acosB-ccosB。

(I) 求 cosB 的值；(II) 若 BA·BC=2，且b=√2，求 a 和 c·b 的值。

解：(I) 由正弦定理得 a=2RsinA，b=2RsinB，c=2RsinC，则 2RsinBcosC=6RsinAcosB-2RsinCcosB，故sinBcosC=3sinAcosB-sinCcosB，可得sinBcosC+sinCcosB=3sinAcosB，即 sin(B+C)=3sinAcosB，可得 sinA=3sinAcosB/sinB。

又sinA≠0，因此 cosB=1/3。

3. 已知向量 m=(sinB,1-cosB)，向量 n=(2,k)，且 m 与 n 所成角为π/3，其中 A、B、C 是△ABC 的内角。

(1) 求角 B 的大小；(2) 求 sinA+sinC 的取值范围。

解：(1) ∠m与∠n所成角为π/3，且 m·n=2sinB+ k(1-cosB)=2√3/2cosB+k√(1-cos²B)，又 m·n=2cosB+k(1-cosB)，解得 k=4/3。

三角函数练习题及答案在学习三角函数的过程中，练习题是非常重要的，能够帮助我们巩固所学的知识，培养解题能力。

下面将给出一些三角函数练习题及其详细答案，希望能对你的学习有所帮助。

一、简单计算题1. 计算sin(30°)的值。

答案：sin(30°) = 1/22. 计算sin(π/3)的值。

答案：sin(π/3) = √3/23. 计算cos(60°)的值。

答案：cos(60°) = 1/24. 计算tan(45°)的值。

答案：tan(45°) = 1二、角度转换题1. 将π/4转换为度数，并计算其sin值。

答案：π/4 ≈ 45°，sin(45°) ≈ √2/22. 将60°转换为弧度，并计算其cos值。

答案：60° = π/3，cos(π/3) = 1/2三、特殊角函数计算题1. 计算sin(π/6) + cos(π/6)的值。

答案：sin(π/6) = 1/2，cos(π/6) = √3/2，所以sin(π/6) + cos(π/6) = 12. 计算tan(π/4) - cot(π/4)的值。

答案：tan(π/4) = 1，cot(π/4) = 1，所以tan(π/4) - cot(π/4) = 0四、和差化积题1. 计算sin(α + β)，已知sin(α) = 1/2，cos(β) = 1/2。

答案：根据和差化积公式，sin(α + β) = sin(α)cos(β) + cos(α)sin(β) = 1/2 * 1/2 + √3/2 * 1/2 = 1/4 + √3/42. 计算cos(α - β)，已知cos(α) = 1/2，sin(β) = √3/2。

答案：根据和差化积公式，cos(α - β) = cos(α)cos(β) + sin(α)sin(β) = 1/2 * 1/2 + √3/2 * √3/2 = 1/4 + 3/4五、三角方程题1. 解方程sin(2x) = 1。