(完整版)杭州市2013职高对口升学高考数学一轮复习考试题一(含答案),推荐文档

2013年杭州市各类高中招生文化考试数 学满分120分，考试时间100分钟参考公式：直棱柱的体积公式：Sh V =（S 为底面积，为高）；圆锥的全面积（表面积）公式：2r rl S ππ+=全（为底面半径，为母线长）；圆柱的全面积（表面积）公式：222r rh S ππ+=全（为底面半径，为高）一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的。

注意可以用多种不同的方法来选取正确答案。

1. 下列“表情图”中，属于轴对称图形的是2. 下列计算正确的是A. 523m m m =+B. 623m m m =⋅C. 1)1)(1(2-=+-m m mD. 12)1(24-=--m m 3. 在□ABCD 中，下列结论一定正确的是A. AC ⊥BDB. ∠A+∠B=180°C. AB=ADD. ∠A ≠∠C4. 若3=+b a ，7=-b a ，则ab =A. -10B. -40C. 10D. 405. 根据2008~2012年杭州市实现地区生产总值（简称GDP ，单位：亿元）统计图所提供的信息，下列判断正确的是A. 2010~2012年杭州市每年GDP 增长率相同B. 2012年杭州市的GDP 比2008年翻一番C. 2010年杭州市的GDP 未达到5500亿元D. 2008~2012年杭州市的GDP 逐年增长6. 如图，设乙图中阴影部分面积甲图中阴影部分面积=k （0>>b a ），则有 A. 2>k B. 21<<kC.121<<k D. 210<<k7. 在一个圆中，给出下列命题，其中正确的是A. 若圆心到两条直线的距离都等于圆的半径，则这两条直线不可能垂直B. 若圆心到两条直线的距离都小于圆的半径，则这两条直线与圆一定有4个公共点C. 若两条弦所在直线不平行，则这两条弦可能在圆内有公共点D. 若两条弦平行，则这两条弦之间的距离一定小于圆的半径8. 如图是某几何体的三视图，则该几何体的体积是A. 318B. 354C. 3108D. 32169. 在Rt △ABC 中，∠C=90°，若AB=4，sinA=，则斜边上的高等于A.2564 B. 2548 C. 516 D. 51210. 给出下列命题及函数x y =，2x y =和xy 1=的图象 ①如果21a a a>>，那么10<<a ； ②如果aa a 12>>，那么1>a ； ③如果a a a>>21，那么01<<-a ； ④如果a a a >>12时，那么1-<a 。

2013年普通高等学校招生全国统一考试(浙江)数学（理科）选择题部分（共50分）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知i 是虚数单位，则(－1+i)(2－i)=A 、－3+iB 、－1+3iC 、－3+3iD 、－1+i 2. 设集合S={x|x>－2}，T={x|x 2+3x －4≤0}，则(C R S )∪T=A 、(－2,1]B 、(－∞,－4]C 、(－∞,1]D 、[1,+∞） 3. 已知x,y 为正实数，则A.2lgx+lgy =2lgx +2lgyB. 2lg(x+y)=2lgx ·2lgyC. 2lgx·lgy=2lgx +2lgy D. 2lg(xy)=2lgx ·2lgy4. 已知函数f(x)=Acos(ωx+ϕ)(A>0, ω>0,ϕ∈R)，则“f(x)是奇函数”是“ϕ=2π”的A 、充分不必要条件B 、必要不充分条件C 、充分必要条件D 、既不充分也不必要条件 5. 某程序框图如图所示，若该程序运行后输出的值是95，则A ．a=4 B.a=5 C.a=6 D.a=76. 已知α∈R ，sin α+2cos α，则tan2α= A ．43 B.34 C.－34 D.－43（第5题图）7. 设△ABC ，P 0是边AB 上一定点，满足P 0B ＝14AB ，且对于边AB 上任一点P ，恒有00PB PC P B PC ⋅≥⋅ ，则A ．∠ABC ＝90°B .∠BAC=90° C.AB=AC D.AC=BC 8. 已知e 为自然对数的底数，设函数f(x)=(e x －1)(x －1)k (k=1,2)，则 A ．当k=1时，f(x)在x=1处取到极小值 B ．当k=1时，f(x)在x=1处取到极大值 C ．当k=2时，f(x)在x=1处取到极小值D ．当k=2时，f(x)在x=1处取到极大值9. 如图F 1、F 2是椭圆C 1：x 24+y 2=1与双曲线C 2的公共焦点，A 、B 分别是C 1、C 2在第二、四象限的公共点，若四边形AF 1BF 2为矩形，则C 2的离心率是 A 、2 B 、3 C 、32 D 、62(第9题图)10. 在空间中，过点A 作平面π的垂线，垂足为B ，记B ＝f π(A)。

2013年普通高等学校招生全国统一考试数学（文科）选择题部分（共50分）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、设集合S={x|x>-2},T={x|-4≤x ≤1},则S ∩T= A 、[-4,+∞） B 、（-2, +∞） C 、[-4,1] D 、(-2,1] 【KS5U 答案】D 【KS5U 解析】如图1所示(2,1]S T ⋂=-，所以选D【考点定位】此题考查集合的运算，利用数轴即可解决此题，体现数形结合思想的应用，此考点是历年来高考必考考点之一，属于简单题。

2、已知i 是虚数单位，则(2+i)(3+i)=A 、5-5iB 、7-5iC 、5+5iD 、7+5i 【KS5U 答案】C 【KS5U 解析】原始=265i i ++=6+5i-1=5+5i,所以选C【考点定位】此题考查复数的乘法运算，考查21i =-这个只是点，属于简单题。

3、若αR ，则“α=0”是“sin α<cos α”的A 、充分不必要条件B 、必要不充分条件C 、充分必要条件D 、既不充分也不必要条件 【KS5U 答案】A【KS5U 解析】此题中，由0α=sin 0cos 1.αα∴=<=，所以是充分条件，反之sin cos αα<，得出33(2,2),()44k k k Z αππ∈-+∈即α不一定等于0，所以是不必要条件选A【考点定位】此题考查充分条件判断和三角函数的知识点；充分和必要条件判断的三种方法 4、设m 、n 是两条不同的直线，α、β是两个不同的平面，A 、若m ∥α，n ∥α,则m ∥nB 、若m ∥α，m ∥β,则α∥βC 、若m ∥n ，m ⊥α,则n ⊥αD 、若m ∥α，α⊥β,则m ⊥β 【KS5U 答案】C 【KS5U 解析】【考点定位】此题考查线线、线面、面面平行与垂直的判定定理和性质定理5、已知某几何体的三视图（单位：cm）如图所示，则该几何体的体积是A、108cm3B、100 cm3C、92cm3D、84cm3【KS5U答案】B【KS5U解析】【考点定位】此题考查三视图知识，多面体的体积计算公式。

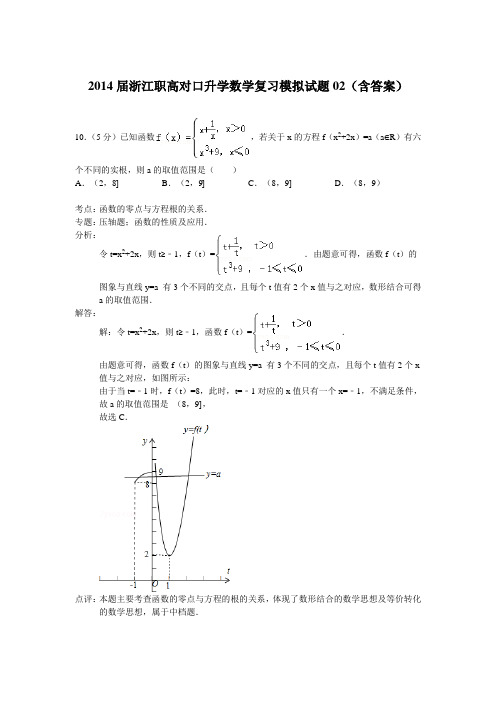
2014届浙江职高对口升学数学复习模拟试题02（含答案）10．（5分）已知函数，若关于x的方程f（x2+2x）=a（a∈R）有六个不同的实根，则a的取值范围是（）A．（2，8]B．（2，9]C．（8，9]D．（8，9）考点：函数的零点与方程根的关系．专题：压轴题；函数的性质及应用．分析：令t=x2+2x，则t≥﹣1，f（t）=．由题意可得，函数f（t）的图象与直线y=a 有3个不同的交点，且每个t值有2个x值与之对应，数形结合可得a的取值范围．解答：解：令t=x2+2x，则t≥﹣1，函数f（t）=．由题意可得，函数f（t）的图象与直线y=a 有3个不同的交点，且每个t值有2个x 值与之对应，如图所示：由于当t=﹣1时，f（t）=8，此时，t=﹣1对应的x值只有一个x=﹣1，不满足条件，故a的取值范围是（8，9]，故选C．点评：本题主要考查函数的零点与方程的根的关系，体现了数形结合的数学思想及等价转化的数学思想，属于中档题．二、填空题：本大题共7小题，每小题4分，共28分.把答案填在答题卷的相应位置. 11．（4分）统计某校1000名学生的数学会考成绩，得到样本频率分布直方图如图所示，规定不低于60分为及格，则及格人数是800．考点：用样本的频率分布估计总体分布；频率分布直方图．专题：图表型；概率与统计．分析：由图知，各段的频率可知，又由总人数为1000，及格人数即为总人数乘上60分以上的频率．解答：解：由图知40﹣50，50﹣60频率分别为0.05，0.15，故不及格的频率是0.2，又学生总数为1000名，所以不及格的有200人，及格有800人．故及格的人数为800人．点评：本题考查用样本频率分布估计总体分布，观察图形是关键，要注意纵坐标表示的是频率，还是．12．（4分）某个几何体的三视图如图所示，则该几何体的体积是cm3．考点：由三视图求面积、体积．分析：由题可知，图形为三棱柱，求体积即可．解答：解：底面积为，高为1，所以体积为V=．点评：本题考查学生的空间想象能力，是基础题．13．（4分）已知O为坐标原点，A（1，1），C（2，3）且，则的坐标是（4，7）．考点：平面向量共线（平行）的坐标表示．专题：计算题；平面向量及应用．分析：设出点B（x，y）的坐标，跟军条件将向量用坐标表示出来，利用向量相等建立x，y 的方程求出x，y的值，即得点B的坐标，再选出正确选项．解答：解：设B（x，y），∵A（1，1），C（2，3）且，∴2（1，2）=（x﹣2，y﹣3），∴，解得，则B（4，7），即=（4，7），故答案为：（4，7）．点评：本题主要考查向量的坐标运算，以及向量相等的应用，解题的关键是求出各个向量的坐标，再根据向量相等建立方程组求出所引入的参数．14．（4分）已知，则不等式f（x）＜9的解集是（﹣2，2）．考点：指数函数单调性的应用．专题：函数的性质及应用．分析：根据解析式需要对x分类：x≥0时和x＜0时，代入对应的关系式列出不等式，再由指数函数的单调性求解，最后要把结果并在一起．解答：解：由题意知，当x≥0时，f（x）=3x＜9=32得，0≤x＜2，当x＜0时，f（x）=＜9=得，﹣2＜x＜0，综上得，不等式f（x）＜9的解集是（﹣2，2），故答案为：（﹣2，2）．点评：本题考查了指数函数的单调性的应用，以分段函数为载体，注意需要根据解析式对自变量进行分类求解，最后要把结果并在一起．15．（4分）若实数x，y满足且z=2x+y的最小值为3，则实数b的值为．考点：简单线性规划的应用．专题：数形结合．分析：先根据约束条件画出可行域，设z=2x+y，再利用z的几何意义求最值，只需求出直线z=2x+y过可行域内的点A时，从而得到b值即可．解答：解：由约束条件作出可行域（如图），当平行直线系y=﹣2x+z经过可行域内的点A（，）时，z取得最小值，即2×+=3，解之得b=．故答案为：．点评：本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．16．（4分）我们把焦点相同，且离心率互为倒数的椭圆和双曲线称为一对“黄金搭档”．已知F1、F2是一对“黄金搭档”的焦点，P是它们在第一象限的交点，当∠F1PF2=60°时，这一对“黄金搭档”中双曲线的离心率是．考点：双曲线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：设F1P=m，F2P=n，F1F2=2c，由余弦定理4c2=m2+n2﹣mn，设a1是椭圆的长半轴，a1是双曲线的实半轴，由椭圆及双曲线定义，得m+n=2a1，m﹣n=2a1，由此能求出结果．解答：解：设F1P=m，F2P=n，F1F2=2c，由余弦定理得（2c）2=m2+n2﹣2mncos60°，即4c2=m2+n2﹣mn，设a1是椭圆的实半轴，a2是双曲线的实半轴，由椭圆及双曲线定义，得m+n=2a1，m﹣n=2a2，∴m=a1+a2，n=a1﹣a2，将它们及离心率互为倒数关系代入前式得a12﹣4a1a2+a12=0，a1=3a2，e1•e2==1，解得e2=．故答案为：．点评：本题考查双曲线和椭圆的简单性质，解题时要认真审题，注意正确理解“黄金搭档”的含义．17．（4分）已知实数a＜0，b＜0，且ab=1，那么的最大值为﹣1．考点：基本不等式．专题：常规题型．分析：将整理得到，利用基本不等式即可求得的最大值．解答：解：由于ab=1，则又由a＜0，b＜0，则，故，当且仅当﹣a=﹣b即a=b=﹣1时，取“=”故答案为﹣1．点评：本题考查基本不等式的应用，牢记不等式使用的三原则为“一正，二定，三相等”．。

2013对口单招高三期中数学试卷2013-2014学年度对口单招高三交流试卷适用班级：高三对口 科目：数学 考试时间：120分钟 总分：150分数学试卷(第I 卷)一 单项选择题（本大题共10小题，每小题4分，共40分．在下列每小题中，选出一个正确答案，请在答题卡上将所选的字母标号涂黑） 1．已知集合}02|{2>--=x x x A ，}2|1||{<-=x x B ，则=B A （ ）A.)3,1(-B.)2,1(-C.)3,2(D.（3,∞-）2．函数y =( )A.［4,+∞)B. (-∞，4]C. (1,+∞)D. (0,4］3．已知ABCD 为矩形，E 是DC 的中点，且=，=，则=（ ） A.ab 21+ B.ab 21- C.ba 21+D.21- 4．函数)32sin(π+=x y 图像的对称轴方程可能是（ ）A.6π-=xB.12π-=xC.6π=xD.12π=x 5．已知等差数列}{na 的前n 项和为nS ，若S 33－S 22＝1，则数列}{na 的公差是( )A.12B.1C.2D.3 6．若复数)(213R a iia z ∈++=是纯虚数，则a 的值为（ ）A.-6B.-2C.4D.6 7．直线01=-+By Ax 在y 轴上的截距是1-，其倾斜角是直线333=-y x 的倾斜角的2倍，则（ ） A.1,3==B A B.1,3-=-=B AC.1,3-==B A D.1,3=-=B A8．函数2)1(22+-+=x a xy 在区间（－∞，]4上是减函数，则实数a 的取值范围是（ ） A ．a ≥3 B ．a ≤－3C ．a ≤5D ．a <－3 9. 二元一次不等式组⎪⎩⎪⎨⎧≤+≥≥200y x y x 表示的平面区域内的整点坐标个数有（ ）2013-2014学年度对口单招高三交流试卷一、单选题二、填空题（本大题共5小题，每小题4分，共20分）11．若54sin -=θ，0tan >θ，则=θcos ．12．已知偶函数)(x f 在),0[+∞上单调递增，且0)1(=f ，则0)(<x f 的解集为 ．13．设锐角三角形ABC 的内角C B A,,的对边分别为cb a ,,，若2sin a b A =，则角B 的大小为 ．14．计算：=⋅64123)41()2(ππii e e ．15．过点)1,2(P 作圆C ：012222=+++-+a ay ax y x的切线有两条，则a 的取值范围是 ．三、解答题（本大题8小题，共90分） 16．（8分）解不等式：02)6(log 22≤-++-x x17．（10分）在ABC ∆中，角A ，B ，C 所对的边分别为c b a ,,，且满足5522cos =A ，3=⋅（1）求ABC ∆的面积 ； （2）6=+c b 若，求a 的值．18．（10分）已知数列}{na 是等差数列，且21=a，12321=++a a a ，（1）求数列}{na 的通项公式； （2）设12+=n a nb ，求数列{nb }的前n 项和.19．（12分）已知函数()4cos sin ()16πf x x x =+- （1）求)(x f 的最小正周期；（2）求)(x f 在区间,64ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值.20．（ 12分）已知函数bb x a x x f 2)1()(22--++=，且)2()1(x f x f -=-,又知x x f ≥)(恒成立.求：(1) )(x f y =的解析式；(2)若函数[]1)(log )(2--=x x f x g ，求函数g(x)的单调增区间.21．（12分）求经过直线0543:1=-+y x l ，2l ：0832=+-y x 的交点M ，且满足下列条件的直线方程： （1）经过原点（2）与直线052=++y x 垂直（3）与圆5)1()1(22=-+-y x 相切.22．（12分）某种商品第一天销售价为42元,以后每天提价2元,且在开始销售的前10天内每天的销售量与上市天数的关系是x(-=(其中x为)xg5150天数).(1)写出上市10天内商品销售价格与天数x的关系式.(2)求销售10天内,哪一天的销售额最大,并求出最大值.1123．（14分）已知方程04222=+--+m y x y x ,(1)若此方程表示圆,求m 的取值范围,(2)若(1)中的圆与直线042=-+y x 相交于N M ,两点,且ON OM ⊥(O 为原点),求m 的值,(3)在(2)的条件下,求以MN 为直径的圆.。

2013年普通高等学校夏季招生全国统一考试数学文史类(浙江卷)选择题部分(共50分)一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．(2013浙江，文1)设集合S＝{x|x＞－2}，T＝{x|－4≤x≤1}，则S∩T＝( )．A．[－4，＋∞) B．(－2，＋∞) C．[－4,1] D．(－2,1]2．(2013浙江，文2)已知i是虚数单位，则(2＋i)(3＋i)＝( )．A．5－5i B．7－5i C．5＋5i D．7＋5i3．(2013浙江，文3)若α∈R，则“α＝0”是sin α＜cos α”的( )．A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件4．(2013浙江，文4)设m，n是两条不同的直线，α，β是两个不同的平面( )．A．若m∥α，n∥α，则m∥n B．若m∥α，m∥β，则α∥βC．若m∥n，m⊥α，则n⊥α D．若m∥α，α⊥β，则m⊥β5．(2013浙江，文5)已知某几何体的三视图(单位：cm)如图所示，则该几何体的体积是( )．A．108 cm3 B．100 cm3 C．92 cm3 D．84 cm36．(2013浙江，文6)函数f(x)＝sin x cos x x的最小正周期和振幅分别是( )．A．π，1 B．π，2 C．2π，1 D．2π，27．(2013浙江，文7)已知a，b，c∈R，函数f(x)＝ax2＋bx＋c.若f(0)＝f(4)＞f(1)，则( )．A．a＞0,4a＋b＝0 B．a＜0,4a＋b＝0 C．a＞0,2a＋b＝0 D．a＜0,2a＋b＝08．(2013浙江，文8)已知函数y＝f(x)的图象是下列四个图象之一，且其导函数y＝f′(x)的图象如右图所示，则该函数的图象是( )．9．(2013浙江，文9)如图，F1，F2是椭圆C1：24x＋y2＝1与双曲线C2的公共焦点，A，B分别是C1，C2在第二、四象限的公共点．若四边形AF1BF2为矩形，则C2的离心率是( )．A．32 D．210．(2013浙江，文10)设a ，b ∈R ，定义运算“∧”和“∨”如下：a ∧b ＝,,,,a a b b a b ≤⎧⎨>⎩a ∨b ＝,,,.b a b a a b ≤⎧⎨>⎩若正数a ，b ，c ，d 满足ab ≥4，c ＋d ≤4，则( )． A ．a ∧b≥2，c ∧d≤2 B ．a ∧b≥2，c ∨d≥2 C ．a ∨b≥2，c ∧d≤2 D ．a ∨b≥2，c ∨d≥2非选择题部分(共100分)二、填空题：本大题共7小题，每小题4分，共28分．11．(2013浙江，文11)已知函数f (x )若f (a )＝3，则实数a ＝__________.12．(2013浙江，文12)从3男3女共6名同学中任选2名(每名同学被选中的机会均等)，这2名都是女同学的概率等于__________．13．(2013浙江，文13)直线y ＝2x ＋3被圆x 2＋y 2－6x －8y ＝0所截得的弦长等于__________． 14．(2013浙江，文14)若某程序框图如图所示，则该程序运行后输出的值等于__________．15．(2013浙江，文15)设z ＝kx ＋y ，其中实数x ，y 满足2,240,240.x x y x y ≥⎧⎪-+≥⎨⎪--≤⎩若z 的最大值为12，则实数k ＝__________.16．(2013浙江，文16)设a ，b ∈R ，若x ≥0时恒有0≤x 4－x 3＋ax ＋b ≤(x 2－1)2，则ab ＝__________.17．(2013浙江，文17)设e 1，e 2为单位向量，非零向量b ＝x e 1＋y e 2，x ，y ∈R .若e 1，e 2的夹角为π6，则||||x b 的最大值等于__________． 三、解答题：本大题共5小题，共72分．解答应写出文字说明、证明过程或演算步骤．18．(2013浙江，文18)(本题满分14分)在锐角△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且2a sin B. (1)求角A 的大小；(2)若a ＝6，b ＋c ＝8，求△ABC 的面积．19．(2013浙江，文19)(本题满分14分)在公差为d 的等差数列{a n }中，已知a 1＝10，且a 1,2a 2＋2,5a 3成等比数列． (1)求d ，a n ；(2)若d ＜0，求|a 1|＋|a 2|＋|a 3|＋…＋|a n|.20．(2013浙江，文20)(本题满分15分)如图，在四棱锥P －ABCD 中，PA ⊥平面ABCD ，AB ＝BC ＝2，AD ＝CD PA ABC ＝120°，G 为线段PC 上的点．(1)证明：BD ⊥平面APC ；(2)若G 为PC 的中点，求DG 与平面APC 所成的角的正切值；(3)若G 满足PC ⊥平面BGD ，求PGGC的值．21．(2013浙江，文21)(本题满分15分)已知a ∈R ，函数f (x )＝2x 3－3(a ＋1)x 2＋6ax . (1)若a ＝1，求曲线y ＝f (x )在点(2，f (2))处的切线方程； (2)若|a |＞1，求f (x )在闭区间[0,2|a |]上的最小值．22．(2013浙江，文22)(本题满分14分)已知抛物线C的顶点为O(0,0)，焦点为F(0,1)．(1)求抛物线C的方程；(2)过点F作直线交抛物线C于A，B两点．若直线AO，BO分别交直线l：y＝x－2于M，N两点，求|MN|的最小值．2013年普通高等学校夏季招生全国统一考试数学文史类(浙江卷)选择题部分(共50分)一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1． 答案：D解析：集合S 与集合T 都表示连续的实数集，此类集合的运算可通过数轴直观表示出来.，故S ∩T ＝{x |－2＜x ≤1}，故选D. 2． 答案：C解析：(2＋i)(3＋i)＝6＋5i ＋i 2，因为i 2＝－1，所以(2＋i)(3＋i)＝5＋5i ，故选C. 3． 答案：A解析：当α＝0时，sin α＜cos α成立；若sin α＜cos α，α可取π6等值，所以“α＝0”是“sin α＜cos α”的充分不必要条件．故选A. 4． 答案：C解析：A 选项中直线m ，n 可能平行，也可能相交或异面，直线m ，n 的关系是任意的；B 选项中，α与β也可能相交，此时直线m 平行于α，β的交线；D 选项中，m 也可能平行于β.故选C. 5． 答案：B解析：由三视图可知，该几何体是如图所示长方体去掉一个三棱锥，故几何体的体积是6×3×6－13×12×3×42＝100(cm 3)．故选B.6． 答案：A解析：由y ＝sin x cos x ＋cos 2x ＝12sin 2x ＋cos 2x ＝πsin 23x ⎛⎫+ ⎪⎝⎭，因为ω＝2，所以T ＝2πω＝π，又观察f (x )可知振幅为1，故选A.7． 答案：A解析：由f (0)＝f (4)知二次函数f (x )＝ax 2＋bx ＋c 对称轴为x ＝2，即22ba-=.所以4a ＋b ＝0，又f (0)＞f (1)且f (0)，f (1)在对称轴同侧，故函数f (x )在(－∞，2]上单调递减，则抛物线开口方向朝上，知a ＞0，故选A.8．答案：B解析：由导函数图象知，函数f (x )在[－1,1]上为增函数．当x ∈(－1,0)时f ′(x )由小到大，则f (x )图象的增长趋势由缓到快，当x ∈(0,1)时f ′(x )由大到小，则f (x )的图象增长趋势由快到缓，故选B. 9． 答案：D解析：椭圆C 1中，|AF 1|＋|AF 2|＝2a ＝4，|F 1F 2|＝2c ＝又四边形AF 1BF 2为矩形，∴∠F 1AF 2＝90°，∴|AF1|2＋|AF2|2＝|F1F2|2，∴|AF1|＝2|AF2|＝2C2中，2c＝2a＝|AF2|－|AF1|＝e==，故选D.10．答案：C解析：由题意知，运算“∧”为两数中取小，运算“∨”为两数中取大，由ab≥4知，正数a，b中至少有一个大于等于2.由c＋d≤4知，c，d中至少有一个小于等于2，故选C.非选择题部分(共100分)二、填空题：本大题共7小题，每小题4分，共28分．11．答案：10解析：由f(a)3，得a－1＝9，故a＝10.12．答案：1 5解析：从3男，3女中任选两名，共有15种基本情况，而从3女中任选2名女同学，则有3种基本情况，故所求事件的概率为31 155=.13．答案：解析：圆的圆心为(3,4)，半径是5，圆心到直线的距离d==，可知弦长l==.14．答案：95解析：该程序框图为循环结构．当k＝1时，S＝1＋112⨯＝32；当k＝2时，3152233S=+=⨯；当k＝3时，5173344S=+=⨯；当k＝4时，7194455S=+=⨯，循环结束，输出95S=.15．答案：2解析：满足条件2,240,240xx yx y≥⎧⎪-+≥⎨⎪--≤⎩的区域D如图阴影部分所示，且A(2,3)，B(4,4)，C(2,0)．作直线l0：y ＝－kx，当k＞0时，y＝－kx为减函数，在B处z最大，此时k＝2；当k＜0时，y＝－kx为增函数，当－k∈10,2⎛⎫⎪⎝⎭时，在B处z取最大值，此时k＝2(舍去)；当－k＞12时，在A处取得最大值，92k=(舍去)，故k＝2.16．答案：－1解析：令x＝1，得0≤1－1＋a＋b≤0，整理，得a＋b＝0，①令x＝－1，得0≤1－(－1)－a＋b≤0，整理，得a－b＝2，②解①②组成的方程组，得1,1. ab=⎧⎨=-⎩∴ab＝－1.17．答案：2解析：因为b≠0，所以b＝x e1＋y e2，x≠0，y≠0.又|b|2＝(x e1＋y e2)2＝x2＋y2＋xy，22222||1||1xyx==++b，不妨设ytx=，则22||||x=b，当2t=-时，t2＋1取得最小值14，此时22||||xb取得最大值，所以||||xb的最大值为2.三、解答题：本大题共5小题，共72分．解答应写出文字说明、证明过程或演算步骤．18．解：(1)由2a sin B及正弦定理sin sina bA B=，得sin A因为A是锐角，所以π3A=.(2)由余弦定理a2＝b2＋c2－2bc cos A，得b2＋c2－bc＝36.又b＋c＝8，所以283bc=.由三角形面积公式S＝12bc sin A，得△ABC19．解：(1)由题意得5a3·a1＝(2a2＋2)2，即d2－3d－4＝0.故d＝－1或d＝4.所以a n＝－n＋11，n∈N*或a n＝4n＋6，n∈N*.(2)设数列{a n}的前n项和为S n，因为d＜0，由(1)得d＝－1，a n＝－n＋11.则当n≤11时，|a1|＋|a2|＋|a3|＋…＋|a n|＝S n＝212122n n-+.当n≥12时，|a1|＋|a2|＋|a3|＋…＋|a n|＝－S n＋2S11＝212122n n-＋110.综上所述，|a1|＋|a2|＋|a3|＋…＋|a n|＝22121,11,22121110,12.22n n nn n n⎧-+≤⎪⎪⎨⎪-+≥⎪⎩20．解：(1)设点O为AC，BD的交点．由AB＝BC，AD＝CD，得BD是线段AC的中垂线．所以O为AC的中点，BD⊥AC.又因为PA⊥平面ABCD，BD⊂平面ABCD，所以PA⊥BD.所以BD⊥平面APC.(2)连结OG .由(1)可知OD ⊥平面APC ，则DG 在平面APC 内的射影为OG ，所以∠OGD 是DG 与平面APC 所成的角．由题意得OG ＝12PA. 在△ABC 中，AC＝ 所以OC ＝12AC在直角△OCD 中，OD2.在直角△OGD 中，tan ∠OGD＝OD OG =. 所以DG 与平面APC(3)连结OG .因为PC ⊥平面BGD ，OG ⊂平面BGD ，所以PC ⊥OG . 在直角△PAC 中，得PC所以GC＝AC OC PC ⋅=从而PG＝5，所以32PG GC =. 21．解：(1)当a ＝1时，f ′(x )＝6x 2－12x ＋6， 所以f ′(2)＝6.又因为f (2)＝4，所以切线方程为y ＝6x －8.(2)记g (a )为f (x )在闭区间[0,2|a |]上的最小值． f ′(x )＝6x 2－6(a ＋1)x ＋6a ＝6(x －1)(x －a )． 令f ′(x )＝0，得到x 1＝1，x 2＝a . 当a ＞1比较f (0)＝0和f (a )＝a 2(3－a )的大小可得g (a )＝23, 3.a a a ⎧⎨(-)>⎩当a ＜－1得g (a )＝综上所述，f (x )在闭区间[0,2|a |]上的最小值为g (a )＝231,1,0,13,3, 3.a a a a a a -<-⎧⎪<≤⎨⎪(-)>⎩22．解：(1)由题意可设抛物线C 的方程为x 2＝2py (p ＞0)，则12p=， 所以抛物线C 的方程为x 2＝4y .(2)设A (x 1，y 1)，B (x 2，y 2)，直线AB 的方程为y ＝kx ＋1.由21,4y kx x y=+⎧⎨=⎩消去y ，整理得x 2－4kx －4＝0， 所以x 1＋x 2＝4k ，x 1x 2＝－4. 从而|x 1－x 2|＝.由11,2,y y x x y x ⎧=⎪⎨⎪=-⎩解得点M 的横坐标1121111122844M x x x x x y x x ===---. 同理点N 的横坐标x N ＝284x -. 所以|MN |x M －x N |284x --＝令4k －3＝t ，t ≠0，则34t k +=. 当t ＞0时，|MN |＝当t ＜0时，|MN |＝综上所述，当253t =-，即43k =-时，|MN |。