- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
Re[G( j)] 0
0
j T
0 T
当 T 时,其虚部和实部均为负,所以其奈氏曲线为第三象限
当 T 时,其实部为负,虚部为正,所以其奈氏曲线为第二象1限8
例5绘制
G(s)
s(2s
10 1)(s2
0.5s
1)
的幅相曲线。
分别计算 0.5 和 2 时的A和
解:G(j)
j(2j
10
G( j) 0 900
2
3
求交点:G(
j )
5[(6
4 2 ) 2(1
j(1 2)
2
)]
令Im[G( j)] 0 即 1
Re[G(
j1)]
5 6 4
11 1
25
令Re[G( j)] 0
1
-25
Im
0 Re
即6 42 0
上式无解,即不存在与虚轴的交点
例题3:绘制 G(s) Kes 的幅相曲线。
Ts 1
G( j ) K e j jT 1
K exp[ j( 57.3 arctan T)]
1 (T )2
Im
(-1,0j) A1
0
K
0
Re
() 900 y A2(y )
A2
() 1800 x A1(x )
17
例4.
已知
G(s)H(s)
K( s 1)
s2(Ts 1) ,
i 1
一、叠加法:先绘制每个环节特性,然后相加减。
二、分段法:利用低频段特点,只需叠加高频线段。
(1) 写出开环频率特性表达式,将所含各典型环节的 转折频率由小到大依次标在频率轴上 。) 作出以分段直线表示的渐近线后,如果需要,再按
典型环节的误差曲线对相应的分段直线进行修正 。
14
例1.绘制非最小相位系统G(s) K-τ s 1
的幅相曲线。
s(Ts 1)
解: G( j ) K (-j 1) j(Tj 1)
起点: G( j0 ) 900 终点: G( j) 0 900 3
tg 1τω 900 tg 1Tω
求交点:
G(
j )
K[-(+T) (T 2 2
))
当 0 ,有A0 ,0 900, Re K T1 T2 Td ,Im
当 ,有 A 0, 1800, Re 0,Im 0
增加有限零点对极坐标图的影响(3)
令 Im 0可求出极坐标图与实轴交点处有 2
1
T1T2 T1Td T2Td
只有当 T1T2 有交点
T1Td
K Td s 1 sT1s 1T2s
1
arctan Td 900 arctan T1 arctan T2
Re
K(T1 T2 Td 2T1T2Td (1 T12 2 )(1 T22 2 )
)
Im
K (1 2(T1T2 T1Td T2Td (1 T12 2 )(1 T22 2 )
当K>0时起点为i×(-900)的无穷远处; 当K<0时起点为-1800 +i×(-900) 的无穷远处。
3
当
0时,频率特性的低频段表达式为G
j
K
j
v
,
故幅频、相频特性分别为:
A G j K , j v
v 900
对于0型系统,v 0, 有A0 K , 0 00; 对于1型系统, v 1, 有A0 , 0 900; 对于2型系统,v 2, 有A0 , 0 1800;
4
A() A1() A2() A3() A4() Ai ()
i 1
4
( ) 1( ) 2( ) 3( ) 4( ) i ( )
i 1
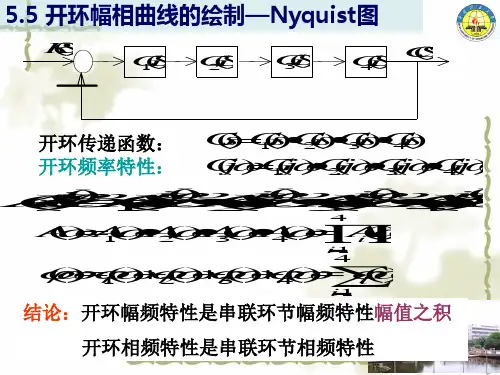
结论:开环幅频特性是串联环节幅频特性幅值之积
开环相频特性是串联环节相频特性相角之和
奈氏图上:相角以逆时针(顺时针)旋转来定义
1.优点
能在一幅图上表
示出系统在整个频率 2
T, , K 0
试分析并绘制>T和<T情况下的幅相曲线。
解:
G(
j )
(
K (j 1) j)2 (Tj 1)
求交点:
起点: G( j0 ) 180 0 终点: G( j) 0 900 2
G(
j )
K[(1 T2 ) j( 2(T 2 2 1)
T )]
时 Im[G( j)] 0
j(1 T2
1)
)]
令 Im[ G( j)] 0
x
1
T Im
K(T )
0
Re
ReG( j) K
x
1
T
相角穿越频率
ReG( j) K
0
例2.绘制G(s)
5(s 2)(s s2(s 1)
3)的幅相曲线。
解:G( j0 ) 1800 () tg-1 tg-1 1800 tg-1
考虑传函
G1s
sT1s
K
1T2s
1
A
K
1 T12 2 1 T22 2
KT1T2 T1 T2
900 arctan T1 arctan T2
Re
(1
K(T1 T2 ) T12 2 )(1 T22
2
)
Im
K (1 T1T2 2 ) (1 T12 2 )(1 T22
n n
即 ( )在 nn 处,相角突变 l 1800
详见下面例题
例题:绘制 解:
G(s)
s(Ts
K
1)(
s2
2 n
1)
的幅相曲线。
G( j )
K
K (T j)
j (Tj
1)
(
(j )2
2 n
1)
(T 2 2
1)(1
2
2 n
)
起点: G( j0 ) 900
n Im
终点: G( j) 0 3600
K(T1 T2 ) (1 T12 2 )(1 T22
2
)
当 0 ,有A0 K,0 0,Re0 K,Im0 0
当 ,有A 0, ,Re 0,Im 0
0.5K
K 0
K 0
1 T1T2
Im
K T1
T1T2 T2
9
增加有限极点对极坐标图的影响
T1 T2 T3
T1T2T3
(4) 作相频特性曲线。根据表达式,在低频、中频和高 频段中各选择若干个频率进行计算,然后连成曲线 。
绘制开环对数幅频曲线(各环节渐近线组成)
1.低频段 min min1, ,m
传递函数:
G(s)
K sυ
斜率: 20 dB/dec
知道直线的斜率后,再确定一点即可确定该直线
方法一 0 min 方法二
使其变现为在考虑在G2传s函 TG11ss1KTT21时ssK,11 的极基坐础标上的,变增化加情有况限。极点,
G1 s
K T1s
1
A K
1 T12 2
arctan T1
ReA
1
K
T12
2
Im
A
KT1 1 T12 2
当 0 ,有 A0 K,0 0,Re0 K,Im0 0
m1 m1
m2 m2
n1 n1
n2 n2
900, 900
1800
,
K K
0 0
特殊地,当开环系统为最小相位系统时,有
n m, Gj K
n m, Gj 0m n 900 0n m 900 5
❖若开环系统存在等幅振荡环节,重数l为正整数,即传函为
1
G(s )H(s )
4
G(
j
)
(
K (1 j 1)( 2 j 1) ( m j j ) (T1 j 1)(T2 j 1) (Tn
1) j
1)
,n m
❖终点:取决于开环传函分子、分母多项式中最小相位
环节和非最小相位环节的阶次和
设开环传函的分子、分母多项式的阶次分别为m和n,记除K
外,分子多项式中最小相位环节的阶次和为m1,非最小相位 环节的阶次和为m2,分母多项式中最小相位环节的阶次和为 n1,非最小相位环节的阶次和为n2,则有m=m1+m2, n=n1+n2
2
)
1
T1T2
0
Im
Re
当 0 ,有A0 ,0 900, Re KT1 T2 ,Im
当 ,有A 0, 2700, Re 0,Im 0
增加有限零点对极坐标图的影响(2)
在G1的基础上增加一个零点考虑传函
A
K 1 Td2 2
1 T12 2 1 T22 2
G2 s
0 1
方法三
La (0 ) 0
La (0 ) 20lg K 20 lg 0
La (1) 20 lg K, 该方法较简单
La (0 ) 20lg K 20 lg0 0 0 v K
tg 1Tn
Im[ G(
j
)]
(T
2
K 2 1)(1
2
2 n
)
0
0
Re
与实轴无交点
n
n
900
tan1 Tn
1800 ,n
0
n ,
0
n 900 tan1 Tn 1800 , n n , 0
增加零、极点对极坐标图的影响
对于最小相位系统,利用后面即将介绍的奈氏判据, 可以根据对(-1, j0)点的包围情况,直接判断系统的稳定性。 因此,讨论增加零、极点对极坐标图形状的影响,对于分 析系统的稳定性来说很重要。 ❖ 增加有限极点
1)((j)2
0.5j