分数乘法知识结构图
- 格式:doc
- 大小:22.50 KB
- 文档页数:1

整数混合运算顺序: 先算乘除,后算加减; 同级运算从左往右按顺序计算; 带括号的先算小括号里面的,再算中括号里面的,然后算括号外面的。
乘法交换律: a × b = b × a 乘法结合律: ( a × b )×c = a × ( b × c ) 乘法分配律: ( a + b )×c = a c + b c (1)两个量的关系:画两条线段图,先画单位一的量,注意两条线段的左边要对齐。
(2)部分和整体的关系:画一条线段图。
1、单位“1” 在分率句中“分数”的前面; 2、或在“占”、“是”、“比”“相当于”的后面。
、求一个数的几分之几是多少:用单位“1”的量×分数=具体量 2、求比一个数多(少)几分之几的数是多少: (1)单位“1”的量×(1+分数)=另一个部分量 (2)已知占单位“1”的几分之几的部分量+单位“1”的量-=要求的部分量1、八个方向:东、南、西、北、东北、东南、西北、西南。
其中,东对西、南对北、东北对西南、西北对东南。
2、地图一般按照“上北下南,左西右东”进行绘制的。
3、观测点不同,物体位置的描述方向也会有所不同。
1、“东偏南30°方向”就是以东为起始边,向南旋转30°的方向。
(“东偏南30°方向”也可以说成“南偏东60°方向”,但一般我们会选择角度更小的描述方法)2、物体的方向和距离是我们在描述物体具体位置时不可或缺的两个因素。
3、物体位置关系的相对性:方向相反,角度相同,距离相同。
角的画法:角的顶点对齐量角器圆心,起始边对齐量角器底边,根据量角器上的度数确定角度并打上点做好标记,连接点与顶点,擦除多余线条。
确定物体位置的方法: 1、先找观测点;2、再定方向(看方向夹角的度数);3、最后确定距离(看比例尺)。
(注:记得标注起点、终点、角度、距离)路线图的描述:每次描述都要说明起点、方向、距离和终点;语句可以用先、然后、接着、最后等词语进行连接。



分数乘法知识点
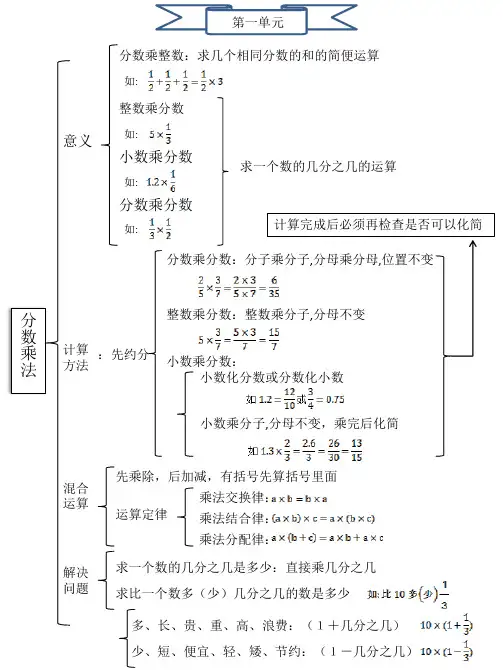
一、分数乘法的意义
1、分数乘整数的意义同整数乘法的意义相同,就是求几个相同加数的和的简便运算
2、一个数乘分数的意义与整数乘法不同的意义:求一个数的几分之几是多少
二、分数乘法的计算方法
1、分数乘整数的计算方法。
分母不变,分子和整数相乘的积作分子。
能约分的要约成最简分数。
2、分数乘以分数的计算方法:分子相乘做分子,分母相乘做分母,能约分的可以先约分。
计算结果要求是最简分数。
3、统一计算方法:整数可以看作分母是一的分数,一个数乘以分数,分子相乘做分子,分母相乘做分母,能约分的可以先约分。
计算结果要求是最简分数。
三、规律:积与因数的大小关系:
真分数相乘积小于任何一个乘数;真分数与假分数相乘积大于真分数小于假分数。
四、解决问题:
1、求一个数的几分之几是多少:单位1 X 分率=分率对应的量
2、比一个数多几分之几的问题:单位1 X比单位1多(少)的分率=比单位1多(少)的量
3、分数连乘的问题:单位1不同,用乘法先求出中间量。
4、分数乘法与加减法综合应用的问题
五、倒数
1、倒数的概念
2、求一个数的倒数。
重点知识
分数乘整数意义:求几个相同分数连加的和的简便运
算。
计算方法:分子相乘的积作分
子,分母相乘的积作分母。
注
意:先约分,再计算。
分数乘
分数
意义:求一个数的几分之几是多少
分数乘加、乘减及乘法运算定律的灵活运用1.分数混合运算的顺序与整数的运算顺序
相同。
2.整数乘法的交换律、结合律和分配律,
对于分
数乘法也适用。
乘法交换律:ab=ba
乘法结合律:(ab)c=a(bc)
乘法分配律:(a+b)c=ac+bc
乘法分配律逆运算:
ac+bc=(a+b)c
解决问题1.求一个数的几分之几是多少。
2.稍复杂的求一个数的几分之几是多少。
单位“1”的量×问题对应倍数=
所求问题
倒数的认识意义:乘积是1的两个数互为倒数。
求倒数方法:分数:交换分子、
分母的位置。
整数:看成分子是1的分数。
小数:先化成分数。