一元二次方程解决动点问题

D
C
Q
A
P
B
才艺展示
1.如图，A、B、C、D为矩形的四个顶点，
AB=16cm，BC=6cm，动点P、Q分别从点A、C
出发，点P以3cm/s的速度
A
D
向点B移动,一直到达B为止； P
E
点Q以2cm/s的速度向点D移动. Q
经过多长时间P、Q两点之间的 B
C
距离是10cm？
才艺展示
2.如图，在Rt△ABC中，AB=BC=12cm，
点D从点A出发，沿AB以2cm/s的速度向B点移
动，移动过程中始终保持DE∥BC，DF∥AC，
问：点D出发多少秒后，四边形DFCE的面积为
20cm2？
C
F
E
AD
B
拓展延伸
3.如图，∠B=90°，AB=6cm,BC=8cm,点P从A点 开始ＡＢ边向点Ｂ以1cm/s速度移动，点Ｑ从Ｂ点 开始沿ＢＣ边向点Ｃ以2cm/s的速度移动.如果P、Q 分别从A、B同时出发， (1)经过几秒，△ PBQ的面积等于8cm2 ？ (2)P到B点后又继续在BC边上前进， Q到C点后又继续在CA边上前进. 经几秒钟S△PCQ=12.6cm²？
x(11 x) 30
整理得 x2 11x 30 0
解得 x1 5, x2 6
当 x1 5 时， 11 x 6;
当 x2 6 时， 11 x 5;
答：长22cm的铁丝能围成面积是30cm2的矩形。
(2) 如果矩形的面积是32cm2,那么
x(11 x) 32
整理得 x2 11x 32 0
一元二次方程的应用（4）
情景创设 一根长为4m的绳子能否围成一个
面积是1m2的矩形？

分析： 点P的运动方向是由A
点Q的运动方向是由B 运动速度都是1cm⁄s C C
运动时间未定
运动距离
点P的运动距离即 AP的长度 点Q的运动距离即 BQ的长度
例：在Rt△ABC中，∠C=90°， AC=8,BC=6.点P由A点出发沿AC方向向点C 匀速移动，点Q由B点出发沿BC方向向点C匀 速移动，它们的速度都是1cm⁄s，几秒后 △PCQ的面积为△ABC面积的一半？
设时间为x，, 则可表示出CP=2x，BQ=x，QC=25-x
等量关系：P、Q两点相距25cm
解：设x秒后P、Q两点相距25cm.
在Rt△QCP中 QC2+PC2=PQ2
（25-x）2+（2x）2=252
5x2-50x=0
x1=0 （舍） ，x2=10 答：10秒后PQ相距25cm。
答：2秒后△PCQ的面积为Rt△ABC面积的一半.
例2：在Rt△ABC中，∠C=90°，AC=30cm， BC=25cm，动点P沿CA方向运动，速度是 2cm⁄s；动点Q从B点出发，沿BC方向运动， 速度是1cm⁄s，几秒后P、Q两点相距25cm？
分析
运动 点P的运动方向是由C 方向
A问题需要注意几个问题： 1、有几个动点？
2、怎样运动？即向哪儿运动？
3、运动的速度、时间、距离分别是多少？
例1：在Rt△ABC中，∠C=90°，AC=8，BC=6. 点P由A点出发沿AC方向向点C匀速移动，点Q 由B点出发沿BC方向向点C匀速移动，它们的速 度都是1cm⁄s，几秒后△PCQ的面积为 △ABC面积的一半？
若设时间为x， 则可表示出AP=x，BQ=x 所以PC=8-x， QC=6-x
等量关系：△PCQ的面积为△ABC面积的一半

一元二次方程动点问题的解题技巧
关于二次函数动点问题的解答方法：
1、求二次函数的图象与x轴的交点坐标，需转化为一元二次方程；
2、求二次函数的最大（小）值需要利用配方法将二次函数由一般式转化为顶点式；
3、根据图象的位置判断二次函数ax+bx+c=0中a,b,c的符号，或由二次函数中a,b,c的符号判断图象的位置，要数形结合；
4、二次函数的图象关于对称轴对称，可利用这一性质，求和已知一点对称的点坐标，或已知与x轴的一个交点坐标，可由对称性求出另一个交点坐标。

5、与二次函数有关的还有二次三项式，二次三项式ax+bx+c﹙a≠0﹚本身就是所含字母x的二次函数。

1)设⊿ ABC位于直线L左侧部分的面积为S,写出S与x之间的函 数关系式; 2)当x为何值时,直线L平分⊿ ABC的面积?
(1)解：∠ BAC=45°,AP=x,
∴当L位于CD的右侧时,与
BC交于点Q
L
AP=X,PB=3-X
C
Q
CD=2,PQ=?
p
由小学学习的比例计算PQ 即：CD:DB=PQ:BQ
∴450=½×(2X-50)×3X
Q
X²-25X-30=0
C
解得：X₁=-5(舍去）;X₂=30
解得：综合以上情况在10S,15S,30S时，△OPQ的面积为450
例2 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始 以1cm/s的速度沿AB边向点B移动,点Q从点B开始以 2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B 同时出发，几秒后⊿ PBQ的面积等于8cm2？
C
通过观察，有两种情况：（1）蚂蚁未爬完OA这段距离
（2）蚂蚁爬完OA这段距离后，再由O点向B爬行
例1 如图OA=OB=50cm,OC是一条射线，OC⊥AB,一
只蚂蚁由点A以2cm/s的速度向B处爬行，同时另一只蚂
蚁由O点以3cm/s的速度沿oc方向爬行，则是否存在这样
的时刻，使两只蚂蚁所在位置与O点组成的三角形的面积
·ALeabharlann RP∴S◇=S△ABC-S△BPQ-S△APQ
∴16=32-½(8-X)²-½×(X)²
整理：x²-8x+16=0
整理：x₁=x₂=4
CQ
B
∴当AP=4cm时，平行四边形PQCR的面积等于16cm2
例4：⊿ABC中,AB=3, ∠ BAC=45°,CD⊥ AB,垂足为D,CD=2,P 是AB上的一动点(不与A,B重合),且AP=x,过点P作直线L与AB垂直.

完整版)一元二次方程解决动点问题研究目标】1.回顾几何图形中动点的行走路程；2.理解等量关系；3.掌握列出关于动点的一元二次方程；4.灵活选用适当的方法解一元二次方程；5.合理舍掉其中一个根。

重点难点】重点：用一元二次方程解决动点问题；难点：分析动点的运动，列出一元二次方程。

导学流程】一）了解感知：一般动态问题的解法是“动中求静”，即按题意确定动点的一个基本位置，然后按照这个基本位置作出恰当的图形，再按照题意逐步探索和求解。

完成课本56页C组1题。

二）深入研究：1.在等腰直角△ABC中,AB=BC=8cm,动点P从A点出发,沿AB向B移动,通过点P引平行于BC,AC的直线与AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm²？2.在△ABC中，∠B=90°，AB=BC=5cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从B开始沿边BC向点C以2cm/s的速度移动，若一动点运动到终点，则另一个也随之停止。

1）如果P、Q分别从A、B两点同时出发，那么几秒后，△PBQ的面积等于4cm²？2）在（1）中，△PBQ的面积能否等于7cm²？说明理由。

三）迁移运用：1.在矩形ABCD中,AB=5cm,BC=7cm,点P从点A开始以1cm/s的速度沿AB边向点B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B同时出发了t秒，直至两动点中某一点到达端点后停止（即0<t<3.5）1)经过几秒后，PQ的长度等于5？DC2)经过几秒后，△BPQ的面积等于4？3)经过几秒后，DP=DQ？XXX学生课堂导学提纲编号：SXTG-025使用时间：2014-9-21编制人：XXX一、知识点梳理本节课我们将研究三角函数的相关概念和性质，包括正弦、余弦、正切等基本概念，以及它们的定义和性质。

二、课堂讲解1.三角函数的定义三角函数是一类最基本的函数，它们的定义涉及到三角形的角度和边长。

24.4 一元二次方程的应用（6）班级___________ 姓名__________ 小组__________ 分数____________ 卷面Ⅰ卷错题重现（20分）1.某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施，调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台，商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？某商场经销的太阳能路标，标价为4000元/个，优惠办法是：一次购买数量不超过80个，按标价收费；一次购买数量超过80个，每多买1个，所购路灯每个可降价8元，但单价最低不能低于3200元/个，若一顾客一次性购买这样的路灯用去516000元，则该顾客实际购买了多少个路灯？Ⅱ卷当堂检测（80分）一、选择题（每题3分，共15分）1.【王沛青】配方法解方程2420x x-+=，下列配方正确的是（）A．2(2)2x-=B．2(2)2x+=C．2(2)2x-=-D．2(2)6x-=2.【马雪爱】一个长为10m的梯子斜靠在墙上，梯子的底端距墙角6m. 若梯子的底端水平向外滑动1m，梯子的顶端滑动（）A 851B 851C 516D 6513.【宋玉珍】直角三角形的面积是30，两直角边长的和是17，则斜边长为（）A 17B 26C 30D 134．【杨阳】某种衬衣价格经过两次降价后，由每件150元降至96元，则平均每次降价的百分率是（）A 20％B 27％C 28％D 32％5．【王沛青（改编）】方程(3)3x x x=）A123,1x x== B123,1x x==- C123x x==121x x==-二、填空题（每空3分，共15分）6.【宋玉珍】两个相邻偶数的积为168，则这两个偶数是____________。

7.【杨阳】当m 时，关于x的方程5)3(72=-+-xxm m是一元二次方程；8.【马雪爱】某果农2006年的年收入为8万元，由于暴雨，2008年年收入减少到5万元，设平均每年的降低率为x，根据题意列出的方程是．9.【宋玉珍】在一次同学聚会时，大家一见面就相互握手．有人统计了一下，大家一共握了45次手，参这次聚会的同学共有人．10.【宋玉珍】如果21xx、是方程0632=--xx的两个根，那么221)(xx-= __.三、解答题11. 【马雪爱20分】解一元二次方程（1）0152=+-xx（2）052222=--xx；（3）23(5)2(5)x x -=- （4）24120x x +-= (用配方法)12.【孙萌10分】在直角三角形ABC 中,AB=BC=12cm ，点D 从点A 开始以2cm/s 的速度沿AB 边向点B 移动,过点D 做DE 平行于BC,DF 平行于AC,点E.F 分别在AC,BC 上,问：点D 出发几秒后四边形DFCE 的面积为20cm ²？13.【杨阳10分】在△ABC 中, AC=50cm, CB=40cm, ∠C=90°,点P 从点A 开始沿AC 边向点C 以2cm/s 的速度移动, 同时另一点Q 由C 点以3cm/s 的速度沿着CB 边移动,几秒钟后, △PCQ 的面积等于450cm ²?14．【王沛青10分】在直角三角形ABC 中，∠B=90°，AB=6厘米，BC=3厘米，点P 从点A 开始沿AB 边向点B 以1cm/s 的速度移动，点Q 从B 开始沿边BC 向点C 以2cm/s 的速度移动，如果P 、Q 分别从A 、B 同时出发，几秒后PQ 距离等于42厘米。

（2）点P，Q出发几秒后， 可使△PCQ 的面积为9 cm2 ? △PCQ的面积能为10cm2?
（3）当点P、Q出发几秒后，
PQ的长度为 4 2 cm？
有关“动点”的运动问题”
1)关键—— 以静代动把动的点进行转换,
2)方法—— 时间变路程
变为线段的长度,
2、在直角三角形ABC中,AB=BC=12cm，点D从点A开始以2cm/s的速度沿AB边向点B移动,过点D做DE平行于BC,DF平行于AC,点E.
Ｅ
Ａ
Ｄ
Ｂ
一个长为10m的梯子斜靠在墙上， 梯子的顶端距地面的垂直距离为8m， 如果梯子的顶端下滑1m，梯子的底端 滑动xm，可列方程为:__________
：如图，△ABC是边长3cm的等边三角形， 动点P、Q同时从A、B两点出发，分别沿AB、 BC方向匀速移动，点P的速度为1cm/s,点Q的 速度为2cm/s，当点Q到达点C时，P、Q两点 停顿运动，设点P的运动时间为t〔s〕，解答 以下问题： 〔1〕当t为何值时，△PBQ是直角三角形？ (2)△PBQ能否为等边三角形？假设能，请求出t 的值，假设不能，说明理由.
点D从点A开始以2cm/s的速度沿AB边 向点B移动,过点D做DE平行于BC,DF平 一元二次方程的应用动点问题
2、在直角三角形ABC中,AB=BC=12cm，点D从点A开始以2cm/s的速度沿AB边向点B移动,过点D做DE平行于BC,DF平行于AC,点E. 点 P 沿 AC 边从点 A 向终点 C 以 1 cm/s的速度移动； 有关“动点”的运动问题”
一元二次方程的应用动点问题
3）常找的数量关系——面积，勾股定理等； （3）当点P、Q出发几秒后，
F分别在AC,BC上,问：点D出发几秒后四边形DFCE的面积为20cm2？ 点 P 沿 AC 边从点 A 向终点 C 以 1 cm/s的速度移动；

2
整理，得 x26x80
解这个方程，得 x1 2,x2 4
Q
0x6 所以2秒或4秒后⊿ PBQ的面
积等于8cm2
A
B
P
例2：等腰直角⊿ ABC中,AB=BC=8cm,动点P从A 点出发,沿AB向B移动,通过点P引平行于BC,AC的 直线及AC,BC分别交于R、Q.当AP等于多少厘米 时,平行四边形PQCR的面积等于16cm2?
A
D
P
（2）P、Q两点从出发开始到几秒时，
点P和点Q的距离是10cm？
Q
B

C
4.如图，在矩形ABCD中，AB=12cm， BC=6cm.点P沿AB边从点A开始向点B以 2cm/s的速度移动，点Q沿DA边从点D开始 向点A以1cm/s的速度移动.如果P、Q同时 出发，用t（s）表示移动的时间（0≤t≤6）. 那么当t为何值时，ΔQAP的面积等于8cm2？
一元二次方程——动点问题
（2）经过多少时间后，S△PCQ的面积为15cm2？
（3）请用配方法说明，何时△PCQ的面积最大， 最大面积是多少？
2．如图，用一块长为50cm、宽为30cm的长方形铁片制 作一个无盖的盒子，若在铁片的四个角截去四个相同的小 正方形，设小正方形的边长为xcm． （1）底面的长AB=_______cm，宽BC=__________cm （用含x的代数式表示） （2）当做成盒子的底面积为300cm2时，求该盒子的容 积．
解：设AP=x，则PR=x，PB=8-x
根据题意得：x8-x 16
整理得：x2 8x 16 0 解这个方程得：x1 x2 4 答：当AP 4cm时，四边形面积为16cm2
CQ
A
R
P
B

Day5：一元二次方程之动点问题一元二次方程解决问题1．动点问题几何图形应用题，关键是将点的运动关系表示出来，找出未知量与已知量的内在联系，根据面积或体积公式列出方程.常见题型：选择题、解答题，求最值问题.易错点：找准动点的关系.中考回顾：常考，求最值或三角形为直角三角形等等.例1如图，点O 在线段AB 上，AO=1，OB=2，OC 为射线，且∠BOC=120°，动点P 以每秒2个单位长度的速度从点O 出发，沿射线OC 作匀速直线运动．设运动时间为t 秒，当△ABP 为直角三角形时，t 的值为（）A．t=1B．t=1或8﹣C．t=8D．t=1或8例2如图，已知△ABC中，∠B=90°，AB=5cm，BC=7cm，点P从点A开始沿AB边向点B以1cm/s 的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，当其中一点停止运动时，另一点也随之停止，其中P、Q不与A、B重合.（1）如果P、Q分别从A、B同时出发，那么几秒后，△PBQ的面积等于4cm2？（2）如果P、Q分别从A、B同时出发，那么几秒后，PQ的长度等于5cm？（3）在（1）中，△PBQ的面积能否等于7cm2？请说明理由.例3如图，在平面直角坐标系中，过原点O及点A（0,2）、C（6,0）作矩形OABC，∠AOC的平分线交AB于点D.点P从点O出发，以每秒2个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒，则当t为何值时，△PBQ为直角三角形？参考答案1.【答案】B【考点】本题考查了动点问题，结合三角形，注意画出图形，帮助理解．【解析】如图1，当∠PAB=90°时，∵∠BOC=120°，∴∠AOP=60°，∴∠APO=30°，∴OP=2OA=2，∵OP=2t，∴t=1；如图2，当∠APB=90°，过P 作PD⊥AB，∵∠OPD=120°﹣90°=30°，∴OD=12∴AD=AO﹣OD=1﹣t，在Rt△ABP 中，根据勾股定理得：AP 2+BP 2=AB 2，即（2+t）222+（1﹣t）2=32，解得：t=8﹣（负值舍去）；当∠ABP=90°时，此情况不存在；综上，当t=1或t=8﹣时，△ABP 是直角三角形．2.【答案】（1）1秒（2）2秒（3）不能【考点】一元二次方程在三角形中动点问题的应用.【解析】（1）设x 秒后，△PBQ 的面积等于4cm².此时，AP=x cm，PB=（5-x）cm，BQ=2x cm，由S △PBQ =4BQ PB 21=∙得()42-521=∙x x ，整理得0452=+-x x ，解得x 1=1，x 2=4.当x=4时，2x=8>7，不合要求.所以1秒后，△PBQ 的面积等于4cm².（2）设x 秒后，PQ 的长度等于5cm.由PB 2+BQ 2=5²得（5-x）²+（2x）²=5²整理得x²-2x=0，解得x 1=0（舍去），x 2=2.经检验，x=2符合要求，所以2秒后，PQ 的长度等于5cm.（3）不能.理由：设x 秒后，△PBQ 的面积等于7cm²，由题意得()72-521=∙x x ，整理得x²-5x+7=0，03-28-25<==∆，此方程无解，所以△PBQ 的面积不可能等于7cm².3.【答案】t=2或55+=t 或5-5=t 【考点】该题考查的是一元二次方程与直角坐标系结合的动点应用题型.【解析】过点P 作PG⊥OC，垂足为G.在Rt△POG 中，∵∠POG=45°，∴∠OPG=45°，∵OP=t 2，∴OG=PG=t，∴点P（t，t），又∵Q（2t，0），B（6,2），根据勾股定理可得PB²=（6-t）²+（2-t）²，QB²=（6-2t）²+2²，PQ²=（2t-t）²+t²=2t².在P、Q 移动过程中，PQ 始终与OD 垂直，容易得知∠BPQ 不可能等于90°.①若∠PQB=90°，则有PQ²+QB²=PB²，即2t²+[（6-2t）²+2²]=（6-t）²+（2-t）²，整理得4t²-8t=0，解得t 1=0（舍去），t 2=2，∴t=2.②若∠PBQ=90°，则有PB²+QB²=PQ²，∴[（6-t）²+（2-t）²]+[（6-2t）²+2²]=2t²，整理得t²-10t+20=0，解得t=5±5.∴当t=2或55+=t 或5-5=t 时，△PQB 为直角三角形.。

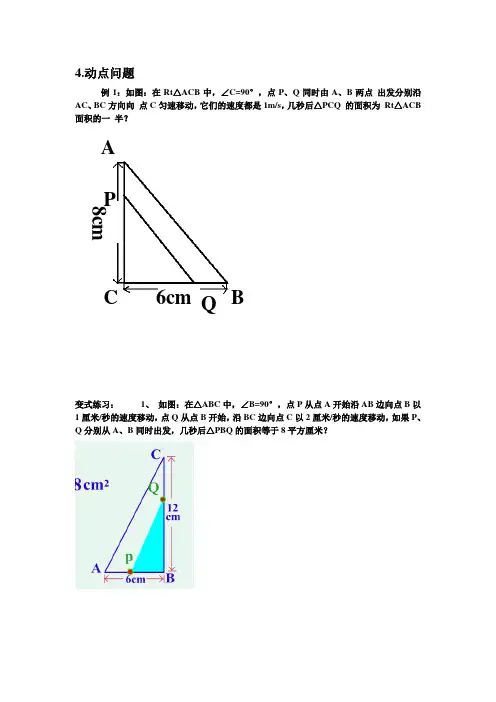
4.动点问题例1：如图：在Rt △ACB 中，∠C=90°，点P 、Q 同时由A 、B 两点 出发分别沿AC 、BC 方向向 点C 匀速移动，它们的速度都是1m/s ，几秒后△PCQ 的面积为 Rt △ACB 面积的一 半？变式练习： 1、 如图：在△ABC 中，∠B=90°，点P 从点A 开始沿AB 边向点B 以1厘米/秒的速度移动，点Q 从点B 开始，沿BC 边向点C 以2厘米/秒的速度移动，如果P 、Q 分别从A 、B 同时出发，几秒后△PBQ 的面积等于8平方厘米？AB C P Q 6cm 8cm2、如图，在△ABC 中，AB=6cm ，AC=12cm 动点D 从A 点出发到B 点为止，运动的速度为1cm/秒；同时动点E 从C 点出发到A 点为止，点E 运动的速度为2cm/秒那么当点A 、D 、E 为顶点的三角形与△ABC 相似时，运动的时间是（ ）3.如图，在矩形ABCD 中，AB=3，BC=4，点P 以每秒2个单位长度的速度从点C 出发，沿CA 向点A 运动；点Q 同时以每秒1个单位长度的速度从点A 出发，沿AB 向点B 运动,设P 、Q 两点移动t 秒（1）求△APQ 与△ABC 相似时t 的值（2）求四边形BCPQ 面积S 与时间t 的关系式（3）求△APQ 为等腰三角形时t 的值B CE D A例2：一艘轮船以20海里/时的速度由西向东航行，途中接到台风警报，台风中心正以40海里/时的速度由南向北移动，距台风中心20 海里的圆形区域(包括边界)都属台10风区.当轮船到A处时，测得台风中心移到位于点A正南方向B处，且AB=100海里.若这艘轮船自A处按原速度继续航行，在途中会不会遇到台风?若会，试求轮船最初遇到台风的时间；若不会，请说明理由.变式练习：某军舰以20节的速度由西向东航行，一艘电子侦察船以30节的速度由南向北航行，它能侦察出周围50海里（包括50海里）范围内的目标。

列一元二次方程解应用题的四种类型（利润、增长率、面积、动点问题）一、商品销售问题售价—进价=利润单价×销售量=销售额一件商品的利润×销售量=总利润某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．如果商场每天要盈利1200元，每件衬衫应降价多少元？分析：设每件衬衫应该降价x元，则每件衬衫的盈利元；商场每天可以多销售件，则商场降价后每天售出的数量为件。

根据：利润=单件的利润╳数量，我们可以列出方程：解这个方程得：答：；例1. 某花圃用花盆培育某种花苗，经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时，平均单株盈利3圆；以同样的栽培条件，若每盆每增加1株，平均单株盈利就减少0.5元.要使每盆的盈利达到10元，每盆应该植多少株？练习：1、某种服装，平均每天可以销售20件，每件盈利44元，在每件降价幅度不超过10元的情况下，若每件降价1元，则每天可多售出5件，如果每天要盈利1600元，每件应降价多少元？2、某化工材料经售公司购进了一种化工原料,进货价格为每千克30元.物价部门规定其销售单价不得高于每千克70元,也不得低于30元.市场调查发现：单价每千克70元时日均销售60kg；单价每千克降低一元,日均多售2kg。

在销售过程中,每天还要支出其他费用500元（天数不足一天时,按一天计算）.如果日均获利1950元,求销售单价3、某商店购进一种商品，进价30元．试销中发现这种商品每天的销售量P(件)与每件的销售价X(元)满足关系：P=100-2X销售量P，若商店每天销售这种商品要获得200元的利润，那么每件商品的售价应定为多少元？每天要售出这种商品多少件？4、某玩具厂计划生产一种玩具熊猫，每日最高产量为４０只，且每日产出的产品全部售出，已知生产ⅹ只熊猫的成本为Ｒ（元），售价每只为Ｐ（元），且ＲＰ与x的关系式分别为R=500+30X，P=170—2X。

一元二次方程与动点问题某些动点问题,常可以建立以时间为未知数的一元二次方程模型.通过求解模型,往往会得到两个实数解,这时要根据实际问题作出取舍.既然是动点问题,结果就有多种可能,因此,有时方程模型的两个实数解都是符合题意的,这一点要注意.解决动点问题,我们必须先弄清楚动点是谁?是单动点还是双动点?运动的路径怎样?方向和速度怎样?运动停止的时间怎样?设运动时间为t ,会用t 表示出各个相关的量,找到等量关系并列出关于t 的方程模型.一般情况下,运动路径由几段构成,就需要分几种情况进行讨论,最后做出总结.例1. 如图,在Rt △ABC 中,︒=∠90ACB ,10=AB cm,8=BC cm,点P 从点A 开始沿射线AC 向点C 以2 cm/s 的速度移动,点Q 从点C 开始沿边CB 向点B 以1 cm/s 的速度移动.如果点P 、Q 分别从点A 、C 同时出发,运动的时间为t s,当点Q 运动到点B 时,两点停止运动.（1）当点P 在线段AC 上运动时,P 、C 两点之间的距离为_________cm;（用含t 的代数式表示）（2）在运动的过程中,是否存在某一时刻,使得△PQC 的面积是△ABC 的面积的61若存在,求出t 的值;若不存在,说明理由.分析:（1）由题意可知,t AP 2=cm ,t CQ =cm .由勾股定理求出6=AC cm .所以()t PC 26-=cm ,即P 、C 两点之间的距离为()t 26-cm ;（2）用含t 的代数式表示△PQC 的面积,由ABC PQC S S ∆∆=61建立关于t 的一元二次方程,由方程是否有实数根说明t 的存在性.由于点P 沿射线AC 运动,且运动停止时间为8s,所以需要分两种情况进行讨论:点P 在线段AC 上运动（t <0≤3）和点P 在线段AC 的延长线上运动（t <3≤8）.解:（1）()t 26-;（2）由题意可知:t CQ =cm.当t <0≤3时,()t PC 26-=cm.∴()t t t t PC CQ S PQC 32621212+-=-=⋅=∆（cm 2） 由486216161=⨯⨯⨯==∆∆ABC PQC S S 可得: 432=+-t t 即0432=+-t t∵()074432<-=⨯--=∆ ∴该方程无实数根;当t <3≤8时,()t PC 26-=cm.∴()46221=-t t ,即0432=--t t 解之得:1,421-==t t （不符合题意,舍去）综上所述,当4=t 时,△PQC 的面积是△ABC 的面积的61. 例2. 如图,在矩形ABCD 中,5=AB cm,6=BC cm,点P 从点A 开始沿AB 向终点B 以1 cm/s 的速度移动,与此同时,点Q 从点B 开始沿BC 向终点C 以2 cm/s 的速度移动,如果点P 、Q 分别从点A 、B 同时出发,当点Q 运动到点C 时,两点停止运动.设运动的时间为t s.（1）填空:=BQ _________,=PB _________;（用含t 的代数式表示）（2）当t 为何值时,PQ 的长度等于102cm? （3）是否存在t 的值,使得五边形APQCD 的面积等于26 cm 2若存在,请求出此时t 的值;若不存在,请说明理由.解:（1）t 2cm,()t -5cm;（2）在Rt △BPQ 中,由勾股定理得:222PQ PB BQ =+∴()()()22210252=-+t t 解之得:3=t∴当3=t 时,102=PQ cm;（3）3065=⨯=⋅=BC AB S ABCD 矩形 cm 2若五边形APQCD 的面积等于26 cm 2,则4=∆BPQ S cm 2 ∴()45221=-⨯t t ∴4,121==t t （不符合题意,舍去）∴存在1=t ,使得五边形APQCD 的面积等于26 cm 2.例3. 如图,在△ABC 中,︒=∠90B ,6=AB cm,12=BC cm,点P 从点A 开始沿AB 边向点B 以1 cm/s 的速度移动,点Q 从点B 开始沿BC 边向点C 以2 cm/s 的速度移动.（1）如果P 、Q 分别从A 、B 同时出发,几秒钟后△PBQ 的面积等于8 cm 2（2）在（1）中,△PBQ 的面积能否等于10 cm 2说明理由. CA BQP解:（1）设x 秒后△PBQ 的面积等于8 cm 2.由题意可知:x AP =cm,x BQ 2=cm∴()x BP -=6cm∵()86221=-⨯=∆x x S PBQ ∴0862=+-x x解之得:4,221==x x∴2s 或4s 后△PBQ 的面积等于8 cm 2;（2）由题意可得:()106221=-⨯x x ∴01062=+-x x∵()0410462<-=⨯--=∆∴该方程无实数根∴△PBQ 的面积不能等于10 cm 2.。

Day5 ：一元二次方程之动点问题一元二次方程解决问题1．动点问题几何图形应用题，要点是将点的运动关系表示出来，找出未知量与已知量的内在联系，依照面积或体积公式列出方程.常有题型：选择题、解答题，求最值问题.易错点：找准动点的关系.中考回顾：常考，求最值或三角形为直角三角形等等.例 1如图，点O 在线段 AB 上，AO=1 ， OB=2 ， OC为射线，且∠BOC=120°，动P点以每秒2个单位长度的速度从点O 出发，沿射线OC 作匀速直线运动．设运动时间为t 秒，当△ABP为直角三角形时，t 的值为（）A．t=1B．﹣33 t=1 或1+8C．t=1+ 33D．t=1 或1+338811 / 4例 2如图，已知△ ABC中，∠ B=90 °，AB=5cm ，BC=7cm ，点 P 从点 A 开始沿 AB 边向点 B 以 1cm/s的速度搬动，点Q 从点 B 开始沿 BC 边向点 C 以 2cm/s的速度搬动，当其中一点停止运动时，另一点也随之停止，其中P、Q 不与 A、B 重合.的面PBQ积等于 4cm 2？（ 1）若是 P、Q 分别从 A、B 同时出发，那么几秒后，△（ 2）若是 P、Q 分别从 A、B 同时出发，那么几秒后，的长度PQ等于 5cm ？（ 3）在（ 1 ）中，△ 的PBQ面积能否等于 7cm 2？请说明原由.例 3如图，在平面直角坐标系中，过原点O 及点 A（ 0,2）、C（ 6,0）作矩OABC形，∠AOC 的均分线交 AB 于点 D. 点 P 从点 O 出发，以每秒 2 个单位长度的速度沿射线OD 方向搬动；同时点 Q 从点 O 出发，以每秒 2 个单位长度的速度沿 x 轴正方向搬动. 设搬动时间为 t 秒，则当 t 为何值时，△ PBQ 为直角三角形？22 / 4参照答案1.【答案】 B【考点】本题观察了动点问题，结合三角形，注意画出图形，帮助理解．【剖析】如图 1 ，当∠PAB=90°时，∵∠BOC=120°，∴∠AOP=60 °，∴∠APO=30 °，∴OP=2OA=2 ，∵ OP=2t ，∴t=1 ；如图 2 ，当∠APB=90 °，过P作 PD⊥ AB ，∵∠ OPD=120°﹣ 90 ° =30 °，1， PD=OP?sin ∠ POD=3 t ，∴ OD= OP=t2∴ AD=AO ﹣ OD=1 ﹣ t ，在 Rt △ ABP中，依照勾股定理得：222，即（2+t2+）（2222，+BPAP=AB 3 t ） + （ 3 t ）+ （ 1﹣ t ）=3﹣331+解得： t=（负值舍去）；8当∠ ABP=90°时，此情况不存在；综上，当 t=1或 t=﹣ABP是直角三角形．1+ 33 时，△82.【答案】（ 1）1秒（ 2）2秒（ 3）不能够【考点】一元二次方程在三角形中动点问题的应用.【剖析】（ 1 ）设x 秒后，△PBQ的面积等于4cm2.此时，AP=xcm ， PB= （ 5-x） cm ， BQ=2xcm ，由 S△PBQ= 1PB BQ 4 得15 - x 2 x 4，22整理得 x 240，解得 x12 5x=1 ，x=4.当 x=4 时， 2x=8>7 ，不合要求.所以 1 秒后，△PBQ的面积等于 4cm2.（ 2 ）设x 秒后，PQ的长度等于5cm.33 / 4由 PB2 +BQ 2=52 得（5-x）2+（2x）2=52整理得 x2-2x=0，解得x1=0（舍去），x2=2.经检验，x=2吻合要求，所以 2 秒后，PQ的长度等于5cm.（ 3 ）不能够.原由：设x秒后，△PBQ的面积等于7cm2 ，12x 7 ，由题意得5- x2， 25-28-3 0，整理得 x2-5x+7=0此方程无解，所以△的PBQ面积不能能等于 7cm2.3.【答案】 t=2或t5 5 或 t 5 - 5【考点】该题观察的是一元二次方程与直角坐标系结合的动点应用题型.【剖析】过点 P 作 PG⊥ OC，垂足为 G.在 Rt △ POG中，∵∠POG=45 °，∴∠OPG=45 °，∵ OP= 2t，∴OG=PG=t ，∴点P（ t ， t ），又∵Q（ 2t ， 0 ），B（ 6,2 ），依照勾股定理可得PB2= （ 6-t ） 2+ （ 2-t） 2 ， QB2= （ 6-2t） 2+22，PQ2= （ 2t-t） 2+t2=2t2.在 P、Q 搬动过程中，始PQ终与 OD 垂直，简单得知∠不BPQ可能等于 90 °.①若∠ PQB=90°，则有PQ2+QB2=PB2，即2t2+[ （ 6-2t ） 2+22]=（ 6-t ） 2+ （ 2-t） 2 ，整理得 4t2-8t=0，解t得1=0 （舍去），t2 =2 ，∴ t=2.②若∠ PBQ=90°，则有PB2+QB2=PQ2，∴ [ （ 6-t） 2+ （ 2-t） 2]+[（ 6-2t） 2+22]=2t2，整理得 t2-10t+20=0，解t=5得±5 .∴当 t=2 或t5 5 或 t 5- 5 时，△PQB为直角三角形.44 / 4。

专题1.7 利用一元二次方程解决几何中的三大动点问题【苏科版】考卷信息：本套训练卷共30题，题型针对性较高，覆盖面广，选题有深度，可加强学生对利用一元二次方程解决几何中的三大动点问题的理解！【类型1 利用一元二次方程解决三角形中的动点问题】1．（2023春·广东江门·九年级校考期中）如图，在等腰中，，，动点P从点A出发沿向点B移动，作，，当的面积为面积的一半时，点P移动的路程为（）A．B．C．D．2．（2023春·浙江·九年级期末）如图，在等腰中，，动点P从点A出发沿折线向点终B以的速度运动，于点Q．设运动时间为，当s时，的面积为．3．（2023春•驻马店期末）如图，已知AG CF，AB⊥CF，垂足为B，AB=BC=3 ，点P是射线AG上的动点（点P不与点A重合），点Q是线段CB上的动点，点D是线段AB的中点，连接PD并延长交BF于点E，连接PQ，设AP=2t，CQ=t，当PQE是以PE为腰的等腰三角形时，t的值为．4．（2023春·广东江门·九年级校考期中）如图，是边长为6cm的等边三角形，动点，同时从，两点出发，分别沿，匀速移动，它们的速度都是2，当点到达点时，，两点都停止运动，设点的运动时间为，解答下列问题：(1)当为何值时，是以为直角的直角三角形？(2)是否存在，使四边形的面积是面积的若存在，求出的值；若不存在，请说明理由．5．（2023春·江苏宿迁·九年级统考期末）如图，在ABC中，∠B＝90°，AB＝12cm，BC＝24cm，动点P 从点A出发沿边AB向点B以2cm/s的速度移动，同时动点Q从点B出发沿边BC向点C以4cm/s的速度移动，当P运动到B点时P、Q两点同时停止运动，设运动时间为ts．(1)BP＝cm；BQ＝cm；（用t的代数式表示）(2)D是AC的中点，连接PD、QD，t为何值时PDQ的面积为40cm26．（2023·浙江金华·九年级期中）如图，在中，厘米，厘米，于点D，动点P从点A出发以每秒1厘米的速度在线段上向终点D运动．设动点运动时间为t秒．（1）求的长；（2）当的面积为15平方厘米时，求t的值；（3）动点M从点C出发以每秒2厘米的速度在射线上运动．点M与点P同时出发，且当点P运动到终点D时，点M也停止运动．是否存在t，使得？若存在，请求出t的值；若不存在，请说明理由．7．（2023春·九年级单元测试）如图，在Rt ABC中，∠BAC＝90°，AB＝AC＝16 cm，AD为BC边上的高，动点P从点A出发，沿A→D方向以cm/s的速度向点D运动，过P点作矩形PDFE(E点在AC上)，设ABP的面积为S1，矩形PDFE的面积为S2，运动时间为t秒(0＜t＜8)．(1)经过几秒钟后，S1＝S2?(2)经过几秒钟后，S1＋S2最大？并求出这个最大值．8．（2023春·江苏淮安·九年级统考期中）Rt ABC中，∠ACB＝90°，AC＝BC＝6，动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动，到达点C停止运动．设运动时间为t秒（1）如图1，过点P作PD⊥AC，交AB于D，若PBC与P AD的面积和是ABC的面积的，求t的值；（2）点Q在射线PC上，且PQ＝2AP，以线段PQ为边向上作正方形PQNM．在运动过程中，若设正方形PQNM与ABC重叠部分的面积为8，求t的值．【类型2 利用一元二次方程解决四边形中的动点问题】1．（2023春·陕西渭南·九年级统考期末）如图，在矩形中，点是上的一个动点，把沿向矩形内部折叠，当点的对应点恰好落在的平分线上时，的长为．2．（2023春·河北邯郸·九年级统考期中）如图所示，A、B、C、D为矩形的四个顶点，，，动点P、Q分别从点A、C同时出发，点P以的速度向B移动，一直到达B为止；点Q以的速度向D移动．当P、Q两点从出发开始秒时，点P和点Q的距离是．（若一点到达终点，另一点也随之停止运动）3．（2023春·山东烟台·九年级统考期中）如图，在矩形中，，，动点P、Q分别以，的速度从点A，C同时出发，沿规定路线移动．(1)若点P从点A移动到点B停止，点Q随点P的停止而停止移动，问经过多长时间P，Q两点之间的距离是？(2)若点P沿着移动，点Q从点C移动到点D停止时，点P随点Q的停止而停止移动，试探求经过多长时间的面积为？4．（2023春·浙江杭州·九年级期中）如图，点，分别在平行四边形的边，上，且，，，动点从点出发沿着线段向终点运动，同时点从点出发沿着折线段向终点运动，且它们同时到达终点，设点运动的路程为，的长度为，且（为常数，）．（1）求证：四边形是平行四边形．（2）求的长．（3）当时，①求的值；②连结，，当为直角三角形时，求所有满足条件的的值．5．（2023春·江西吉安·九年级校联考期中）如图，在ABD中，AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC（1）求证：四边形ABCD是菱形．（2）如果OA,OB(OA>OB)的长（单位：米）是一元二次方程的两根，求AB的长以及菱形ABCD的面积．（3）若动点M从A出发，沿AC以2m/s的速度匀速直线运动到点C,动点N从B 出发，沿BD以1m/s的速度匀速直线运动到点D，当M运动到C点时运动停止．若M、N同时出发，问出发几秒钟后，MON 的面积为？6．（2023春·浙江·九年级期中）如图，在四边形ABCD中，AD∥BC，∠B＝90°，AD＝16cm，AB＝12cm，BC＝21cm，动点P从点B出发，沿射线BC的方向以每秒2cm的速度运动到C点返回，动点Q从点A出发，在线段AD上以每秒1cm的速度向点D运动，点P，Q分别从点B，A同时出发，当点Q运动到点D时，点P随之停止运动，设运动的时间为t（秒）．（1）当t为何值时，四边形PQDC是平行四边形；（2）当t为何值时，以C，D，Q，P为顶点的四边形面积等于60cm2？（3）当0<t<10.5时，是否存在点P，使PQD是等腰三角形？若存在，请直接写出所有满足要求的t的值；若不存在，请说明理由．7．（2023春·浙江杭州·九年级校考期中）如图，平行四边形ABCD中，AB＝4cm，AD＝2cm，∠C＝30°．点P以2cm/s的速度从顶点A出发沿折线A﹣B﹣C向点C运动，同时点Q以1cm/s的速度从顶点A出发沿折线A﹣D﹣C向点C运动，当其中一个动点到达末端停止运动时，另一点也停止运动．设运动时间为ts．（1）求平行四边形ABCD的面积；（2）求当t＝0.5s时，APQ的面积；（3）当APQ的面积是平行四边形ABCD面积的时，求t的值．8．（2023春·广东惠州·九年级惠州一中校考开学考试）如图，AC是正方形ABCD的对角线，AD＝8，E是AC的中点，动点P从点A出发，沿AB方向以每秒1个单位的速度向终点B运动，同时动点Q从点B出发，以每秒2个单位的速度先沿BC方向运动到点C，再沿CD方向向终点D运动，以EP、EQ为邻边作平行四边形PEQF，设点P运动的时间为t秒（0＜t＜8）(1)当t＝1时，试求PE的长；(2)当点F恰好落在线段AB上时，求BF的长；(3)在整个运动过程中，当▱PEQF为菱形时，求t的值．9．（2023春·九年级单元测试）如图，正方形的边长为，动点从点出发，以的速度沿方向向点运动，动点从点出发，以的速度沿方向向点运动，若，两点同时出发，运动时间为．(1)连接，，，当为何值时，面积为(2)当点在上运动时，是否存在这样的的值，使得是以为腰的等腰三角形？若存在，请求出符合条件的的值；若不存在，请说明理由．10．（2023·江苏·九年级假期作业）如图，在矩形中，，，动点P、Q分别从点A、C同时出发，点P以的速度向点B移动，一直到点B为止，点Q以的速度向点D移动（点P停止移动时，点Q也停止移动）．设移动时间为t（s）．连接，．(1)用含t的式子表示线段的长：__________；__________．(2)当t为何值时，P、Q两点间的距离为？(3)当t为何值时，四边形的形状可能为矩形吗？若可能，求出t的值；若不可能，请说明理由．【类型3 利用一元二次方程解决坐标系中的动点问题】1．（2023春·陕西渭南·九年级统考期末）如图①，在矩形中，，对角线、相交于点，动点由点出发，沿运动，设点的运动路程为，的面积为，与的函数关系图像如图②所示，则边的长为（）A．3 B．4 C．5 D．62．（2023·河南驻马店·统考三模）如图，在平面直角坐标系中，矩形的边在y轴上，边在x轴上，点B的坐标是，D为边上一个动点，把沿折叠，若点A的对应点恰好落在矩形的对角线上，则点的坐标为（）A．B．C．D．3．（2023春·四川德阳·九年级统考期末）如图①，在中，于D，，，，点E 是上一动点（不与点A，D重合），在内作矩形，点F在上，点G、H在上，设，连接．(1)设矩形的面积为，的面积为，令，求y关于x的函数解析式；（要求写出自变量的取值范围）(2)如图②，点M是（1）中得到的函数图象上的任意一点，N的坐标为，，当为等腰三角形时，求点M的坐标．4．（2023春·广东佛山·九年级佛山市华英学校校考期中）如图，平面直角坐标系中，已知点，点，过点作轴的平行线，点是在直线上位于第一象限内的一个动点，连接，．(1)求出__________；(2)若平分，求点的坐标；(3)已知点是直线上一点，若是以为直角边的等腰直角三角形，求点的坐标.5．（2023春·广东江门·九年级江门市福泉奥林匹克学校校考期中）已知，如图：在直角坐标系中，正方形AOBC的边长为4，点D，E分别是线段AO，BO上的动点，D点由A点向O点运动，速度为每秒1个单位，E点由B点向O点运动，速度为每秒2个单位，当一个点停上运动时，另一个点也随之停止，设运动时间为t（秒）(1)如图1，当t为何值时，DOE的面积为6；(2)如图2，连接CD，与AE交于一点，当t为何值时，CD⊥AE；(3)如图3，过点D作DG OB，交BC于点G，连接EG，当D，E在运动过程中，使得点D，E，G三点构成等腰三角形，求出此时t的值6．（2023春·浙江·九年级期中）如图直角坐标系中直线与轴正半轴、轴正半轴交于，两点，已知，，，分别是线段，上的两个动点，从出发以每秒个单位长度的速度向终点运动，从出发以每秒个单位长度的速度向终点运动，两点同时出发，当其中一点到达终点时整个运动结束，设运动时间为（秒）．(1)求线段的长，及点的坐标；(2)为何值时，的面积为；(3)若为的中点，连接，，以，为邻边作平行四边形．是否存在时间，使轴恰好将平行四边形的面积分成两部分，若存在，求出的值．7．（2023春·浙江宁波·九年级校考期中）在平面直角坐标系中，A，B点的坐标分别为（0，4），（-4，0），点坐标为，点是射线BO上的动点，满足BE=1.5OP，以，为邻边作．（1）当m=2时，求出PE的长度；（2）当m﹥0时，是否存在m的值，使得的面积等于ABO面积的，若存在求出m的值，若不存在，请说明理由；（3）当点Q在第四象限时，点Q关于E点的对称点为Q′，点Q′刚好落在AB上时，求m的值（直接写出答案）．8．（2023春·浙江·九年级期中）如图1，在平面直角坐标系中，已知四边形的顶点，分别在轴和轴上．直线经过点，与轴交于点已知，，平分，交于点，动点从点出发沿着线段向终点运动，动点从点出发沿着线段向终点运动，，两动点同时出发，且速度相同，当点到达终点时点也停止运动，设．(1)求和的长；(2)如图，连接，，求证：四边形为平行四边形；(3)如图，连接，，当为直角三角形时，求所有满足条件的值．9．（2023春·浙江·九年级期中）如图1，已知，点O为坐标原点，点C在x轴的正半轴上．在中，边的角平分线交于点D．（1）求两点的坐标；（2）若点M是直线上的一个动点，点是坐标平面上的点，以点为顶点的四边形是菱形时，请直接写出点的坐标；（3）如图2，点P从点O出发，以每秒个单位长度的速度沿射线方向移动：同时点Q从点O出发，以每秒2个单位长度的速度沿射线方向移动，连结，设移动时间t秒．当t为何值时，是直角三角形．10．（2023春·重庆·九年级重庆市育才中学校联考期中）在平面直角坐标系中，直线l经过点和点．点C的横坐标为，点D为线段的中点．(1)求直线l的解析式．(2)如图1，若点P为线段上的一个动点，当的值最小时，求出点P坐标．(3)在（2）的条件下，点Q在线段上，若是等腰三角形，请直接写出满足条件的点Q的横坐标，并写出其中一个点Q的横坐标的求解过程．11．（2023春·河南南阳·九年级南阳市第三中学校考期末）如图，平行四边形位于直角坐标系中，为坐标原点，点，点交轴于点动点从点出发，沿方向以每秒1个单位长度的速度终点运动，同时动点从点出发，沿射线的方向以每秒2个单位长度的速度运动，当点运动到点时，点随之停止运动，运动时间为t（秒）．（1）用t的代数式表示：________，________（2）若以A，B，E，F为顶点的四边形是平行四边形时，求t的值．（3）当恰好是等腰三角形时，求t的值．12．（2023·辽宁沈阳·统考一模）已知：如图，在平面直角坐标系中，矩形AOBC的顶点C的坐标是（6，4），动点P从点A出发，以每秒1个单位的速度沿线段AC运动，同时动点Q从点B出发，以每秒2个单位的速度沿线段BO运动，当Q到达O点时，P，Q同时停止运动，运动时间是t秒（t＞0）．（1）如图1，当时间t＝秒时，四边形APQO是矩形；（2）如图2，在P，Q运动过程中，当PQ＝5时，时间t等于秒；（3）如图3，当P，Q运动到图中位置时，将矩形沿PQ折叠，点A，O的对应点分别是D，E，连接OP，OE，此时∠POE＝45°，连接PE，求直线OE的函数表达式．专题1.7 利用一元二次方程解决几何中的三大动点问题【苏科版】考卷信息：本套训练卷共30题，题型针对性较高，覆盖面广，选题有深度，可加强学生对利用一元二次方程解决几何中的三大动点问题的理解！【类型1 利用一元二次方程解决三角形中的动点问题】1．（2023春·广东江门·九年级校考期中）如图，在等腰中，，，动点P从点A出发沿向点B移动，作，，当的面积为面积的一半时，点P移动的路程为（）A．B．C．D．【答案】B【分析】设AP＝x cm，则PB＝（8−x）cm，求出∠A＝45°，∠APR＝90°，得到PR＝P A＝x cm，然后根据▱PQCR 的面积为ABC面积的一半列方程求解即可．【详解】解：设AP＝x cm，则PB＝（8−x）cm，∵∠B＝90°，AB＝BC＝8cm，∴∠A＝45°，∵PR BC，∴∠APR＝90°，∴PR＝P A＝x cm，∵▱PQCR的面积为ABC面积的一半，∴，解得：，∴点P移动的路程为4cm．故选：B．【点睛】本题主要考查了平行四边形的性质，一元二次方程的应用，根据几何图形的性质得出方程是解题的关键．2．（2023春·浙江·九年级期末）如图，在等腰中，，动点P从点A出发沿折线向点终B以的速度运动，于点Q．设运动时间为，当s时，的面积为．【答案】或【分析】利用等腰直角三角形的性质求出AB，设时间为秒，分和两种情况结合三角形面积分别计算．【详解】解：∵在等腰中，，，∴，，．∵于点．∴设当时间为秒时，的面积为．当时，，，，即，解得：或（舍去）．当时，，，，即，解得：或（舍去）．综上所述：当或秒时，的面积为．故答案为：或．【点睛】本题考查了等腰直角三角形的性质，勾股定理，三角形面积公式，解一元二次方程，解题的关键是理解点的运动情况，注意分类讨论．3．（2023春•驻马店期末）如图，已知AG CF，AB⊥CF，垂足为B，AB=BC=3 ，点P是射线AG上的动点（点P不与点A重合），点Q是线段CB上的动点，点D是线段AB的中点，连接PD并延长交BF于点E，连接PQ，设AP=2t，CQ=t，当PQE是以PE为腰的等腰三角形时，t的值为．【答案】或【分析】以B为原点、直线CF为x轴，直线AB为y轴，建立直角坐标系，先证明AP=BE，即可得E点坐标为(2t,0)，CQ=t，BQ=3-t，P点坐标为(-2t,3)，C点坐标为(-3,0)，A点坐标为(0,3)，Q点坐标为(t-2,0)，根据Q点在线段BC上，P点不与A点重合，可得0＜t＜3，进而有BE=2t，BQ=3-t，QE=BQ+EB=3+t，利用勾股定理有：，，，根据PQE是以PE为腰的等腰三角形，分类讨论：当PQ=PE时，当QE=PE时两种情况，即可求解．【详解】以B为原点、直线CF为x轴，直线AB为y轴，建立直角坐标系，如图，∵，AB⊥CF，∴AB⊥AG，∴∠GAB=∠ABF=90°，∵D点为AB中点，∴AD=BD，∴结合∠ADP=∠BDE可得APD≌△BED，∴AP=BE，∵AP=2t，∴BE=2t，∴E点坐标为(2t,0)，∵AB=BC=3，∴CQ=t，即BQ=3-t，P点坐标为(-2t,3)，C点坐标为(-3,0)，A点坐标为(0,3)，∴Q点坐标为(t-3,0)，∵Q点在线段BC上，P点不与A点重合，∴0＜t＜3，∵BE=2t，BQ=3-t，∴QE=BQ+EB=3+t，∴利用勾股定理有：，，，根据PQE是以为腰的等腰三角形，分类讨论：当PQ=PE时，有，整理：，解得（负值舍去），当QE=PE时，有，整理：，解得（0舍去），综上所述：t的值可以为，．故答案为：，．【点睛】本题考查了等腰三角形的性质、构建直角坐标系、勾股定理、全等三角形的判定与性质、一元二次方程的应用等知识，构建直角坐标系是快速解答此题的关键．解答时，需注意分类讨论的思想．4．（2023春·广东江门·九年级校考期中）如图，是边长为6cm的等边三角形，动点，同时从，两点出发，分别沿，匀速移动，它们的速度都是2，当点到达点时，，两点都停止运动，设点的运动时间为，解答下列问题：(1)当为何值时，是以为直角的直角三角形？(2)是否存在，使四边形的面积是面积的若存在，求出的值；若不存在，请说明理由．【答案】(1)1(2)不存在，理由见解析【分析】（1）当时，利用直角三角形的性质建立方程，解方程即可得；（2）假设存在某一时刻，使四边形的面积是面积的，从而可得，过点作于点，利用直角三角形的性质和勾股定理可得，再利用三角形的面积公式建立方程，然后利用一元二次方程根的判别式进行分析即可得出答案．【详解】（1）由题意得：，，为等边三角形，，当点到达点时，，则，∵，，，即，解得，符合题意；（2）不存在，使四边形的面积是面积的，理由如下：假设存在某一时刻，使四边形的面积是面积的，由（1）得：，，如图，过点作于点，，，，整理得：，此方程根的判别式为，方程无解，所以假设不成立，即不存在，使四边形的面积是面积的．【点睛】本题考查了等边三角形的性质、含角的直角三角形的性质、勾股定理、一元二次方程的应用等知识点，正确建立关于时间的方程是解题关键．5．（2023春·江苏宿迁·九年级统考期末）如图，在ABC中，∠B＝90°，AB＝12cm，BC＝24cm，动点P 从点A出发沿边AB向点B以2cm/s的速度移动，同时动点Q从点B出发沿边BC向点C以4cm/s的速度移动，当P运动到B点时P、Q两点同时停止运动，设运动时间为ts．(1)BP＝cm；BQ＝cm；（用t的代数式表示）(2)D是AC的中点，连接PD、QD，t为何值时PDQ的面积为40cm2【答案】(1)（12﹣2t）；4t(2)t＝2或4【分析】（1）根据速度×时间=路程，列出代数式即可；（2）如图，过点D作DH⊥BC于H，利用三角形中位线定理求得DH的长度；然后根据题意和三角形的面积列出方程，求出方程的解即可．【详解】（1）根据题意得：AP＝2tcm，BQ＝4tcm，所以BP＝（12﹣2t）cm．故答案是：（12﹣2t）；4t．（2）如图，过点D作DH⊥BC于H，∵∠B＝90°，即AB⊥BC，∴AB∥DH，又∵D是AC的中点，∴BH=BC＝12cm，DH是ABC的中位线，∴DH AB＝6cm，根据题意，得-（12﹣2t）-（24﹣4t）×6-2t×12＝40，整理，得t2﹣6t+8＝0，解得：t1＝2，t2＝4，即当t＝2或4时，PBQ的面积是40cm2．【点睛】本题主要考查了一元二次方程的应用，解题的关键是读懂题意，找到关键描述语，列出等量关系．6．（2023·浙江金华·九年级期中）如图，在中，厘米，厘米，于点D，动点P从点A出发以每秒1厘米的速度在线段上向终点D运动．设动点运动时间为t秒．（1）求的长；（2）当的面积为15平方厘米时，求t的值；（3）动点M从点C出发以每秒2厘米的速度在射线上运动．点M与点P同时出发，且当点P运动到终点D时，点M也停止运动．是否存在t，使得？若存在，请求出t的值；若不存在，请说明理由．【答案】（1）12厘米；（2）6秒；（3）存在t的值为2或或，使得S PMD=S ABC．【分析】①根据等腰三角形性质和勾股定理解答即可；②根据直角三角形面积求出PD×DC×=15即可求出t；③根据题意列出PD、MD的表达式解方程组，由于M在D点左右两侧情况不同，所以进行分段讨论即可，注意约束条件．【详解】解：（1）∵AB=AC=13，AD⊥BC，∴BD=CD=5cm，且∠ADB=90°，∴AD2=AC2-CD2∴AD=12cm．（2）AP=t，PD=12-t，又∵由PDM面积为PD×DC=15，解得PD=6，∴t=6．（3）假设存在t，使得S PMD=S ABC．①若点M在线段CD上，即0≤t≤时，PD=12-t，DM=5-2t，由S PMD=S ABC，即×(12−t)(5−2t)＝5，2t2-29t+50=0解得t1=12.5（舍去），t2=2．②若点M在射线DB上，即≤t≤12．由S PMD=S ABC得(12−t)(2t−5)＝5，2t2-29t+70=0解得t 1＝，t 2＝．综上，存在t的值为2或或，使得S PMD=S ABC．【点睛】此题关键为利用三角形性质勾股定理以及分段讨论，在解方程时，注意解是否符合约束条件．7．（2023春·九年级单元测试）如图，在Rt ABC中，∠BAC＝90°，AB＝AC＝16 cm，AD为BC边上的高，动点P从点A出发，沿A→D方向以cm/s的速度向点D运动，过P点作矩形PDFE(E点在AC 上)，设ABP的面积为S1，矩形PDFE的面积为S2，运动时间为t秒(0＜t＜8)．(1)经过几秒钟后，S1＝S2?(2)经过几秒钟后，S1＋S2最大？并求出这个最大值．【答案】(1) t＝4 (2) t＝6【分析】分别根据运动方式列出面积S1,S2关于t的函数关系，第一问令面积相等，第二问配方求最值. 【详解】解：S1＝×8×t＝8t，S2＝t(8－t)＝－2t2＋16t，(1)由8t＝－2t2＋16t，解得t1＝4，t2＝0(舍去)，∴当t＝4秒时，S1＝S2(2)∵S1＋S2＝8t＋(－2t2＋16t)＝－2(t－6)2＋72，∴当t＝6时，S1＋S2最大，最大为72【点睛】关于x的两次三项式，可以配方化为只含一个变量的式子，再利用平方的非负性求最值,必要是需要引入二次函数的内容求最值.8．（2023春·江苏淮安·九年级统考期中）Rt ABC中，∠ACB＝90°，AC＝BC＝6，动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动，到达点C停止运动．设运动时间为t秒（1）如图1，过点P作PD⊥AC，交AB于D，若PBC与P AD的面积和是ABC的面积的，求t的值；（2）点Q在射线PC上，且PQ＝2AP，以线段PQ为边向上作正方形PQNM．在运动过程中，若设正方形PQNM与ABC重叠部分的面积为8，求t的值．【答案】（1）t1＝2，t2＝4；（2）t的值为或2时，重叠面积为8．【分析】（1）先求出ABC的面积，然后根据题意可得AP＝t，CP＝6﹣t，然后再PBC与P AD的面积和是ABC的面积的，列出方程、解方程即可解答；（2）根据不同时间段分三种情况进行解答即可.【详解】（1）∵Rt ABC中，∠ACB＝90°，AC＝BC＝6，∴S ABC＝×6×6＝18，∵AP＝t，CP＝6﹣t，∴△PBC与P AD的面积和＝t2+×6×（6﹣t），∵△PBC与P AD的面积和是ABC的面积的，∴t2+×6×（6﹣t）＝18×，解之，得t1＝2，t2＝4；（2）∵AP＝t，PQ＝2AP，∴PQ＝2t，①如图1，当0≤t≤2时，S＝（2t）2﹣t2＝t2＝8，解得：t1＝，t2＝﹣（不合题意，舍去），②如图2，当2≤t≤3时，S＝×6×6﹣t2﹣（6﹣2t）2＝12t﹣t2＝8，解得：t1＝4（不合题意，舍去），t2＝（不合题意，舍去），③如图3，当3≤t≤6时，S＝6×6﹣t2＝8，解得：t1＝2，t2＝﹣2（不合题意，舍去），综上，t的值为或2时，重叠面积为8．【点睛】本题考查了三角形和矩形上的动点问题，根据题意列出方程和分情况讨论是解答本题的关键.【类型2 利用一元二次方程解决四边形中的动点问题】1．（2023春·陕西渭南·九年级统考期末）如图，在矩形中，点是上的一个动点，把沿向矩形内部折叠，当点的对应点恰好落在的平分线上时，的长为．【答案】或【分析】过点A1作A1F⊥BC于F，根据等腰直角三角形的判定可得为等腰直角三角形，设CF==x，从而得出BF= 7－x，CA1=，然后根据折叠的性质可得AB==5，再利用勾股定理求出x，即可求出结论．【详解】解：过点A1作A1F⊥BC于F∵四边形ABCD为矩形，平分∴∴△为等腰直角三角形，设CF==x则BF=BC－CF=7－x，CA1==由折叠的性质可得AB==5在Rt中，即解得：x1=3，x2=4∴CA1=或故答案为：或．【点睛】此题考查的是矩形与折叠问题，掌握矩形的性质、折叠的性质、勾股定理、等腰直角三角形的判定及性质和解一元二次方程是解决此题的关键．2．（2023春·河北邯郸·九年级统考期中）如图所示，A、B、C、D为矩形的四个顶点，，，动点P、Q分别从点A、C同时出发，点P以的速度向B移动，一直到达B为止；点Q以的速度向D移动．当P、Q两点从出发开始秒时，点P和点Q的距离是．（若一点到达终点，另一点也随之停止运动）【答案】2或【分析】设当P、Q两点从出发开始x秒时，点P和点Q的距离是10cm，此时，，利用勾股定理即可得出关于x的一元二次方程，解之即可得出结论．【详解】解：设当P、Q两点从出发开始x秒时，点P和点Q的距离是，此时，，如图，过作于，∵四边形是矩形，∴四边形，是矩形，∴，，∴，则，根据题意得：，解得：，．答：当P、Q两点从出发开始到2秒或秒时，点P和点Q的距离是10cm．故答案为：2或．【点睛】本题考查了矩形的性质与判定，一元二次方程的应用以及勾股定理，利用勾股定理找出关于x的一元二次方程是解题的关键．3．（2023春·山东烟台·九年级统考期中）如图，在矩形中，，，动点P、Q分别以，的速度从点A，C同时出发，沿规定路线移动．(1)若点P从点A移动到点B停止，点Q随点P的停止而停止移动，问经过多长时间P，Q两点之间的距离是？(2)若点P沿着移动，点Q从点C移动到点D停止时，点P随点Q的停止而停止移动，试探求经过多长时间的面积为？【答案】(1)或；(2)4秒或6秒．【分析】（1）过点P作于E，构造直角三角形，利用勾股定理即可求得；（2）根据点P的三个位置进行分类讨论，表示出的底和高，代入面积公式即可求得；【详解】（1）解：过点P作于E，设x秒后，点P和点Q的距离是．，∴，；∴经过或，P、Q两点之间的距离是；（2）解：连接．设经过后PBQ的面积为．①当时，，∴，即，解得；②当时，，，则，解得，（舍去）；③时，，则，解得（舍去）．综上所述，经过4秒或6秒，的面积为．【点睛】本题考查了动点问题，相关知识点有：勾股定理求长度，解一元二次方程等知识点，分类讨论是本题的解题关键．4．（2023春·浙江杭州·九年级期中）如图，点，分别在平行四边形的边，上，且，，，动点从点出发沿着线段向终点运动，同时点从点出发沿着折线段向终点运动，且它们同时到达终点，设点运动的路程为，的长度为，且（为常数，）．（1）求证：四边形是平行四边形．（2）求的长．（3）当时，①求的值；②连结，，当为直角三角形时，求所有满足条件的的值．【答案】（1）见解析；（2）8；（3）①2；②，，【分析】（1）根据已知证明即可得证；（2）根据题，当时，，令时，即可求得；（3）①当到达点时，点到达点，此时,则，令求得，可得，结合已知条件可得；②由①可得，是等边三角形，分情况讨论，当在上，时，根据含30度角的直角三角形的性质，可得；当时，过点分别作，垂足为,可得四边形是矩形，分别求得,根据勾股定理列出方程，解一元二次方程即可，当时，如图，过点作于点,同理通过勾股定理求得，当点在上时，观察图形可知不存在直角三角形．【详解】四边形是平行四边形；即四边形是平行四边形；（2）依题意，设点运动的路程为，的长度为，。