一元二次方程应用(动点问题)
- 格式:doc
- 大小:479.00 KB
- 文档页数:4





4.动点问题例1:如图:在Rt △ACB 中,∠C=90°,点P 、Q 同时由A 、B 两点 出发分别沿AC 、BC 方向向 点C 匀速移动,它们的速度都是1m/s ,几秒后△PCQ 的面积为 Rt △ACB 面积的一 半?变式练习: 1、 如图:在△ABC 中,∠B=90°,点P 从点A 开始沿AB 边向点B 以1厘米/秒的速度移动,点Q 从点B 开始,沿BC 边向点C 以2厘米/秒的速度移动,如果P 、Q 分别从A 、B 同时出发,几秒后△PBQ 的面积等于8平方厘米?AB C P Q 6cm 8cm2、如图,在△ABC 中,AB=6cm ,AC=12cm 动点D 从A 点出发到B 点为止,运动的速度为1cm/秒;同时动点E 从C 点出发到A 点为止,点E 运动的速度为2cm/秒那么当点A 、D 、E 为顶点的三角形与△ABC 相似时,运动的时间是( )3.如图,在矩形ABCD 中,AB=3,BC=4,点P 以每秒2个单位长度的速度从点C 出发,沿CA 向点A 运动;点Q 同时以每秒1个单位长度的速度从点A 出发,沿AB 向点B 运动,设P 、Q 两点移动t 秒(1)求△APQ 与△ABC 相似时t 的值(2)求四边形BCPQ 面积S 与时间t 的关系式(3)求△APQ 为等腰三角形时t 的值BCE D A例2:一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20 海里的圆形区域(包括边界)都属台10风区.当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,请说明理由.变式练习:某军舰以20节的速度由西向东航行,一艘电子侦察船以30节的速度由南向北航行,它能侦察出周围50海里(包括50海里)范围内的目标。

Day5:一元二次方程之动点问题一元二次方程解决问题1.动点问题几何图形应用题,关键是将点的运动关系表示出来,找出未知量与已知量的内在联系,根据面积或体积公式列出方程.常见题型:选择题、解答题,求最值问题.易错点:找准动点的关系.中考回顾:常考,求最值或三角形为直角三角形等等.例1如图,点O 在线段AB 上,AO=1,OB=2,OC 为射线,且∠BOC=120°,动点P 以每秒2个单位长度的速度从点O 出发,沿射线OC 作匀速直线运动.设运动时间为t 秒,当△ABP 为直角三角形时,t 的值为()A.t=1B.t=1或8﹣C.t=8D.t=1或8例2如图,已知△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s 的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点停止运动时,另一点也随之停止,其中P、Q不与A、B重合.(1)如果P、Q分别从A、B同时出发,那么几秒后,△PBQ的面积等于4cm2?(2)如果P、Q分别从A、B同时出发,那么几秒后,PQ的长度等于5cm?(3)在(1)中,△PBQ的面积能否等于7cm2?请说明理由.例3如图,在平面直角坐标系中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒2个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒,则当t为何值时,△PBQ为直角三角形?参考答案1.【答案】B【考点】本题考查了动点问题,结合三角形,注意画出图形,帮助理解.【解析】如图1,当∠PAB=90°时,∵∠BOC=120°,∴∠AOP=60°,∴∠APO=30°,∴OP=2OA=2,∵OP=2t,∴t=1;如图2,当∠APB=90°,过P 作PD⊥AB,∵∠OPD=120°﹣90°=30°,∴OD=12∴AD=AO﹣OD=1﹣t,在Rt△ABP 中,根据勾股定理得:AP 2+BP 2=AB 2,即(2+t)222+(1﹣t)2=32,解得:t=8﹣(负值舍去);当∠ABP=90°时,此情况不存在;综上,当t=1或t=8﹣时,△ABP 是直角三角形.2.【答案】(1)1秒(2)2秒(3)不能【考点】一元二次方程在三角形中动点问题的应用.【解析】(1)设x 秒后,△PBQ 的面积等于4cm².此时,AP=x cm,PB=(5-x)cm,BQ=2x cm,由S △PBQ =4BQ PB 21=∙得()42-521=∙x x ,整理得0452=+-x x ,解得x 1=1,x 2=4.当x=4时,2x=8>7,不合要求.所以1秒后,△PBQ 的面积等于4cm².(2)设x 秒后,PQ 的长度等于5cm.由PB 2+BQ 2=5²得(5-x)²+(2x)²=5²整理得x²-2x=0,解得x 1=0(舍去),x 2=2.经检验,x=2符合要求,所以2秒后,PQ 的长度等于5cm.(3)不能.理由:设x 秒后,△PBQ 的面积等于7cm²,由题意得()72-521=∙x x ,整理得x²-5x+7=0,03-28-25<==∆,此方程无解,所以△PBQ 的面积不可能等于7cm².3.【答案】t=2或55+=t 或5-5=t 【考点】该题考查的是一元二次方程与直角坐标系结合的动点应用题型.【解析】过点P 作PG⊥OC,垂足为G.在Rt△POG 中,∵∠POG=45°,∴∠OPG=45°,∵OP=t 2,∴OG=PG=t,∴点P(t,t),又∵Q(2t,0),B(6,2),根据勾股定理可得PB²=(6-t)²+(2-t)²,QB²=(6-2t)²+2²,PQ²=(2t-t)²+t²=2t².在P、Q 移动过程中,PQ 始终与OD 垂直,容易得知∠BPQ 不可能等于90°.①若∠PQB=90°,则有PQ²+QB²=PB²,即2t²+[(6-2t)²+2²]=(6-t)²+(2-t)²,整理得4t²-8t=0,解得t 1=0(舍去),t 2=2,∴t=2.②若∠PBQ=90°,则有PB²+QB²=PQ²,∴[(6-t)²+(2-t)²]+[(6-2t)²+2²]=2t²,整理得t²-10t+20=0,解得t=5±5.∴当t=2或55+=t 或5-5=t 时,△PQB 为直角三角形.。


一元二次方程的应用-动点问题1.如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P,Q分别从点A,B同时开始移动,点P的速度为1cm/秒,点Q的速度为2cm/秒,点Q移动到点C后停止,点P也随之停止运动.下列时间瞬间中,能使△PBQ的面积为15cm2的是()A.2秒钟B.3秒钟C.4秒钟D.5秒钟2.如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.(1)P、Q两点从出发开始到几秒时,四边形PBCQ的面积为33cm2;(2)P、Q两点从出发开始到几秒时,点P和点Q的距离是10cm.3.等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度做直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ 的面积为S.(1)求出S关于t的函数关系式;=S△ABC?(2)当点P运动几秒时,S△PCQ(3)作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.4.如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1cm2?5.已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于6cm2?(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于5cm?(3)在(1)中,△PQB的面积能否等于8cm2?说明理由.6.如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向C点以2cm/s的速度移动.(1)如果点P,Q分别从A,B同时出发,经过几秒钟后,△PBQ的面积等于8cm2;(2)如果点P,Q分别从A,B同时出发,并且点P到B点后又继续在BC边上前进,点Q到点C后又继续在CA边上前进,则经过几秒钟后,△PCQ的面积等于12.6cm2.7.如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q 从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:(1)经过6秒后,BP=cm,BQ=cm;(2)经过几秒后,△BPQ是直角三角形?(3)经过几秒△BPQ的面积等于cm2?8.如图,长方形ABCD(长方形的对边相等,每个角都是90°),AB=6cm,AD=2cm,动点P、Q分别从点A、C同时出发,点P以2厘米/秒的速度向终点B移动,点Q以1厘米/秒的速度向D移动,当有一点到达终点时,另一点也停止运动.设运动的时间为t,问:(1)当t=1秒时,四边形BCQP面积是多少?(2)当t为何值时,点P和点Q距离是3cm?(3)当t=以点P、Q、D为顶点的三角形是等腰三角形.(直接写出答案)9.已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,同时点Q从点B开始沿BC边向点C以2cm/s的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为x秒,(1)求几秒后,△PBQ的面积等于6cm2?(2)求几秒后,PQ的长度等于5cm?(3)运动过程中,△PQB的面积能否等于8cm2?说明理由.10.如图,菱形ABCD中,AC,BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线运动到C,动点N从B出发沿BD方向以1m/s匀速直线运动到D,若M,N同时出发,问出发后几秒钟时,△MON的面积为?11.如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,若P点沿AB向B以1cm/s的速度移动,点Q从B沿BC向C以2cm/s的速度移动,问几秒后,△PBQ的面积为8cm2?12.如图,在△ABC中,AB=6cm,BC=7cm,∠ABC=30°,点P从A点出发,以1cm/s的速度向B点移动,点Q从B点出发,以2cm/s的速度向C点移动.如果P、Q两点同时出发,经过几秒后△PBQ的面积等于4cm2?同时点Q从点B开始沿BC这向点C以2cm/s的速度移动.当一个点到达终点时另一点也随之停止运动,运动时间为x秒(x>0)(1)求几秒后,PQ的长度等于5cm;(2)运动过程中,△PQB的面积能否等于8cm2?说明理由.14.已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题:(1)经过秒时,求△PBQ的面积;(2)当t为何值时,△PBQ是直角三角形?(3)是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出t的值;不存在请说明理由.点Q从点B开始沿BC边向点C以2cm/s的速度移动.(1)如果P,Q分别从A,B同时出发那么几秒后,PQ的长度等于cm?(2)在(1)中,△PQB的面积能否等于7cm2?请说明理由.16.在长方形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C 时,两点停止运动.设运动时间为t秒.(1)填空:BQ=,PB=(用含t的代数式表示);(2)当t为何值时,PQ的长度等于5cm?(3)是否存在t的值,使得五边形APQCD的面积等于26cm2?若存在,请求出此时t的值;若不存在,请说明理由.17.如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.(1)若点P从点A移动到点B停止,点P、Q分别从点A、C同时出发,问经过2s时P、Q两点之间的距离是多少cm?(2)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?(3)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P 随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?18.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A开始沿射线AC向点C以2cm/s的速度移动,与此同时,点Q从点C开始沿边CB向点B以1cm/s的速度移动.如果P、Q分别从A、C同时出发,运动的时间为ts,当点Q运动到点B时,两点停止运动.(1)当点P在线段AC上运动时,P、C两点之间的距离cm.(用含t的代数式表示)(2)在运动的过程中,是否存在某一时刻,使得△PQC的面积是△ABC面积的.若存在,求t的值;若不存在,说明理由.19.如图,在矩形ABCD中,AB=10cm,AD=8cm,点P从点A出发沿AB以2cm/s的速度向点终点B运动,同时点Q从点B出发沿BC以1cm/s的速度向点终点C运动,它们到达终点后停止运动.(1)几秒后,点P、D的距离是点P、Q的距离的2倍;(2)几秒后,△DPQ的面积是24cm2.20.如图所示,A、B、C、D是矩形的四个顶点,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止,点Q以2cm/s的速度向点D移动(1)P,Q两点从出发开始到几秒时,四边形PBCQ的面积为33cm2?(2)P,Q两点从出发开始到几秒时,点P和点Q的距离第一次是10cm?。


列一元二次方程解应用题的四种类型(利润、增长率、面积、动点问题)一、商品销售问题售价—进价=利润单价×销售量=销售额一件商品的利润×销售量=总利润某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.如果商场每天要盈利1200元,每件衬衫应降价多少元?分析:设每件衬衫应该降价x元,则每件衬衫的盈利元;商场每天可以多销售件,则商场降价后每天售出的数量为件。
根据:利润=单件的利润╳数量,我们可以列出方程:解这个方程得:答:;例1. 某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3圆;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?练习:1、某种服装,平均每天可以销售20件,每件盈利44元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出5件,如果每天要盈利1600元,每件应降价多少元?2、某化工材料经售公司购进了一种化工原料,进货价格为每千克30元.物价部门规定其销售单价不得高于每千克70元,也不得低于30元.市场调查发现:单价每千克70元时日均销售60kg;单价每千克降低一元,日均多售2kg。
在销售过程中,每天还要支出其他费用500元(天数不足一天时,按一天计算).如果日均获利1950元,求销售单价3、某商店购进一种商品,进价30元.试销中发现这种商品每天的销售量P(件)与每件的销售价X(元)满足关系:P=100-2X销售量P,若商店每天销售这种商品要获得200元的利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?4、某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出,已知生产ⅹ只熊猫的成本为R(元),售价每只为P(元),且RP与x的关系式分别为R=500+30X,P=170—2X。
专题八:一元二次方程应用类型中的动点问题(有答案)➢知识指引所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类问题.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.解题时要注意动点的起始位置和终止位置、运动方向,有时还要关注动点的运动速度,注意在运动过程中寻找等量关系.动点问题思路剖析问题1:动点问题的处理框架是什么?答:读题标注,整合信息(即明确所研究的背景图形)问题2:分析运动过程需要关注四要素是什么?答:①起点、终点、速度:标注到图形中,以示说明②时间范围根据路程、时间和速度的公式s=vt,已知动点的速度,结合基本图形中线段长的研究,可以确定动点的运动时间③状态转折状态转折即点的运协发生变化的时刻,常体现在动点的运动方向,运动速度发生了改变④目标或结论导向根据题意作出图形,有序操作(分段作图并求解)问题3:在分析几何特征,表达时,常见表达线段长的方式有哪些?答:①路程即线段长,可根据s=vt直接进行表达已走路程或未走路程②根据研究几何特征的需求进行表达,即要利用动点的运动情况,又要结合背景图形信息➢知识点睛由点的运动产生的几何问题称为动点问题.动点问题的解决方法:1.研究背景图形并标注;;2.分析运动过程,并适时分段;3.表达线段长,建等式和方程.➢典型例题【例1】如图,在△ABC中,∠B=90°,AB=9,BC=12,点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果P.Q分别从A.B同时出发,当点Q运动到点C时,两点停止运动,问:(1)填空:BQ= ,PB= (用含t的代数式表示)(2)经过几秒,PQ的长为6√2cm?(3)经过几秒,△PBQ的面积等于8cm2?【解答】(1)根据题意得:BQ=2t,PB=9-t.故答案为:2t;9-t.(2)根据题意得:(9-t)2+(2t)2=72,,t2=3,解得:t1=35秒或3秒,PQ的长为6√2cm.∴经过35×(9-t)×2t=8,(3)根据题意得:12解得:t1=8,t2=1.∵0≤t≤6,∴t=1.答:经过1秒,△PBQ的面积等于8cm2.【例2】如图,在四边形ABCD中,AD∥BC ,∠C=90°, BC=16,DC=12 ,AD=21 ,动点P从点D出发,沿线段 DA的方向以每秒2个单位长的速度运动;动点Q从点 C出发,在线段 CB 上以每秒1个单位长的速度向点B运动;点P,Q 分别从点D,C同时出发,当点P运动到点 A 时,点Q随之停止运动,设运动的时间为t秒).(1)当t=2时,求△BPQ的面积;(2)若四边形ABQP为平行四边形,求运动时间t.(3)当t为何值时,以 B,P,Q为顶点的三角形是等腰三角形?备用图【解答】(1)如图,过点P 作PM ⊥BC 于M ,则四边形PDCM 为矩形,∴PM=DC=12.∵QB=16-t ,当t=2时,则BQ=14,则S=12QB ⋅PM =12×14×12=84;(2)当四边形ABQP 是平行四边形时,AP=BQ,即21-2t=16-t .解得t=5. ∴当t=5时,四边形ABQP 是平行四边形.(3)由图可知,CM=PD=2t ,CQ=t ,若以B 、P 、Q 为顶点的三角形是等腰三角形,可以分为以下三种情况:①若PQ=BQ ,在Rt △PMQ 中,PQ 2=t 2+122,由PQ 2= BQ 2, 得t 2+ 122= (16-t)2 解得t=72;②若BP=BQ ,在Rt △PMB 中,PB 2=(16-2t)2+122,由PB 2= BQ 2得(16-2t)2+ 122= (16-t)2,即3t 2+-32t+144= 0.此时,Δ= (-32)2 -4×3×144= -704<0, 所以此方程无解,所以PB ≠BQ ;③若PB=PA ,由PB 2= PQ 2,得t 2+ 122= (16-2t)2 + 122 , 解得t 1=163,t 2=16,(不合题意,舍去);综上所述,当t=72或163时,以B ,P ,Q 为顶点的三角形是等腰三角形.➢ 跟踪训练1.如图,在△ABC 中,AC=50cm ,BC=40 cm ,∠C =90°,点P 从点A 开始沿AC 边向点C 以每秒2 cm 的速度匀速移动,同时另一点Q 由C 点开始以每秒3 cm 的速度沿着射线CB 匀速移动,当△PCQ 的面积等于300 cm 2运动时间为( ).A. 5秒B. 20秒C. 5秒或20秒D. 不确定【解答】由题意,得AP=2t ,CQ=3t ,∴PC=50-2t ,∴12•PC•CQ=300,∴12•(50-2t )•3t=300,解得t=20或5,∴t=20s 或5s 时,△PCQ 的面积为300m 2.故选:C .2.如图,在△ABC 中,∠B=90°,AB=6cm ,BC=8cm .点P 从点A 开始沿AB 边向点B 以1cm/s 的速度移动,点Q 从点B 开始沿BC 边向点C 以2cm/s 的速度移动.若P 、Q 两点同时出发,当点P 运动到点B 时,P ,Q 两点同时停止运动,当三角形PQB 的面积是三角形ABC 的面积的三分之一时,所需时间为( )A .4 sB .2 sC .2或4sD .3或4s【解答】设经过x 秒,三角形PQB 的面积是三角形ABC 的面积的三分之一.∵P 、Q 移动t 秒时,AP=t ,BQ=2t ,则PB=AB-AP=6-t ,∴S △P B Q =13,由S △A B C =12AB•BC=12×6×8=24,当S △P B Q =13S △A B C 时,则12•2t(6-t )=13×24,整理,得t 2-6t+8=0,解得t 1=2,t 2=4,即当t=2或4时,△PBQ 的面积等于△ABC 的面积的三分之一. 故选:C .3.如图,在Rt △ABC 中,∠B =90°,AB =BC =12 cm ,点D 从点A 开始沿边AB 以2 cm/s 的速度向点B 移动,移动过程中始终保持四边形DFCE (点E ,F 分别在AC ,BC 上)为平行四边形,则出发________s 时,四边形DFCE 的面积为20 cm 2.【解答】设点D从点A出发x s时,四边形DFCE的面积为20 cm2.由题意,得12×12×12−4x22−(12−2x)22=20,解得x1=1,x2=5,故答案为:1或5.4.某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点A、B,以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系l=t2+3t(t≥0),乙以8cm/s的速度匀速运动,半圆的长度为42cm.(1)甲运动4s后的路程是多少?(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?【解答】(1)当t=4s 时,l=t2+3t=16+12=28(cm).答:甲运动4s后的路程是28cm.(2)由图可知,甲乙第一次相遇时走过的路程为半圆21cm,甲走过的路程为t2+3t,乙走过的路程为4t,则t2+3t+8t=42,解得:t1=3,t2=-14(不合题意,舍去).答:甲、乙从开始运动到第一次相遇时,它们运动了3s.(3)由图可知,甲乙第一次相遇时走过的路程为三个半圆3×42=126cm,则t2+3t+8t=126,解得:t=7或t=-18(不合题意,舍去).答:甲、乙从开始运动到第二次相遇时,它们运动了7s .5.如图,在矩形ABCD 中,AB=6cm ,BC=12cm ,点P 从点A 开始以1cm/s 的速度沿AB 边向B 移动,点Q 从点B 开始以2cm/s 的速度沿BC 边向点C 移动.如果P 、Q 分别从A 、B 同时出发,当点Q 运动到点C 时,P 、Q 两点同时停止运动. (1)是否存在某一时刻使得△PQD 的面积等于8cm 2?若存在,求出运动的时间;若不存在,说明理由.(2)几秒后,△PQD 是以DP 为斜边的直角三角形.【解答】(1)不存在,理由如下:设出发秒x 时△DPQ 的面积等于8cm 2. ∵S 矩形A B C D -S △A P D -S △B P Q -S △C D Q =S △D P Q ,∴6×12-12×12×x -12×(6-x )•2x -12(12-2x )×6=8,∴x 2-6x+28=0,∵∆=b 2-4ac=36-4×28=-76<0,∴原方程无实数根,即不存在某一时刻使得△PQD 的面积等于8cm 2. (2)∵∠A=∠B=∠C=90°,∴PD 2=t 2+122,PQ 2=(6-t )2+(2t )2,QD 2=(12-2t )2+62, ∵△PQD 是以DP 为斜边的直角三角形,∴PD 2=PQ 2+QD 2,即t 2+122=(6-t )2+(2t )2+(12-2t )2+62, 整理得2t 2-15t+18=0,解之得t 1=6,t 2=32,即当t 为32秒或6秒时,△PQD 是以PD 为斜边的直角三角形.6.如图,在矩形ABCD 中,AB=6cm ,BC=12cm ,点P 从点B 出发沿线段BC 、CD 以2cm/s 的速度向终点D 运动;同时,点Q 从点C 出发沿线段CD 、DA 以1cm/s 的速度向终点A 运动(P 、Q 两点中,只要有一点到达终点,则另一点运动立即停止).(1)运动停止后,哪一点先到终点?另一点离终点还有多远?(2)在运动过程中,△APQ 的面积能否等于22cm 2?若能,需运动多长时间?若不能,请说明理由【解答】(1)点P 从开始到运动停止用的时间为:(12+6)÷2=9s,点Q 从开始到运动停止用的时间为:(6+12)÷1=18s, ∵9<18,只要有一点到达终点,则另一点运动立即停止,∴点P 先到终点,此时点Q 离终点的距离是:(6+12)-1×9=9cm, 答:点P 先到终点,此时点Q 离终点的距离是9cm ;(2)在运动过程中,△APQ 的面积能等于22cm 2,当P 从点B 运动到点C 的过程中,设点P 运动时间为as ,∵△APQ 的面积能否等于22cm 2, ∴12×6-2a×62−(12−2a)×a2−(6−a)×122=22,解得,此方程无解;当点P 从C 到D 的过程中,设点P 运动的时间为(b+6)s ,∵△APQ 的面积能否等于22cm 2, ∴12×6-(6+2b)×122−b(6−2b)2=22,解得,b 1=1,b 2=14(舍去),即需运动6+1=7s ,△APQ 的面积能等于22cm 2.7.如图,在矩形ABCD 中,AB=5cm ,BC=6cm ,点P 从点A 开始沿边AB 向终点B 以1cm/s 的速度移动,与此同时,点Q 从点B 开始沿边BC 向终点C 以2cm/s 的速度移动.如果P ,Q 分别从A ,B 同时出发,当点Q 运动到点C 时,两点停止运动,设运动时间为t 秒. (1)填空:BQ=__________,PB=_________;(用含t 的代数式表示) (2)当t 为何值时,PQ 的长度等于5cm ?(3)是否存在t 的值,使得五边形APQCD 的面积等于26cm 2?若存在,请求出此时t 的值;若不存在,请说明理由.【解答】(1)∵P从点A开始沿边AB向终点B以1cm/s的速度移动,∴AP=tcm.∵AB=5cm,∴PB=(5-t)cm.∵点Q从点B开始沿边BC向终点C以2cm/s的速度移动,∴BQ=2tcm;(2)由题意,得(5-t)2+(2t)2=52.解得t1=0(不合题意,舍去),t2=2.所以当t=2秒时,PQ的长度等于5cm.(3)存在,t=1秒时,能够使得五边形APQCD的面积等于26cm2.由矩形ABCD的面积是5×6=30cm2,若五边形APQCD的面积等于26cm2,则△PBG的面积为30-26=4 cm2,=4.解得t1=4(不合题意,舍去),t2=1.即(5-t)×2t×12即当t=1秒时,五边形APQCD的面积等于26cm2.8. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动,到达点C停止运动.点Q在射线PC上,且PQ =2AP,以线段PQ为边向上作正方形PQNM.在运动过程中,设运动时间为t秒,(1)当N点落在BC上时,t= 秒;(2)若设正方形PQNM与△ABC重叠部分的面积为8,求t的值.备用图【解答】(1)当N 落在BC 上时,Q 点在C 处,此时CP+AP=2t+t=6,∴t=2,.故填:2(2)∵AP =t ,PQ =2AP ,∴PQ =2t ,①如图1,当0≤t ≤2时,S =(2t )2﹣12t 2=72t 2=8, 解得:t 1=47√7,t 2=﹣47√7(不合题意,舍去),②如图2,当2≤t ≤3时,S =12×6×6﹣12t 2﹣12(6﹣2t )2=12t ﹣25t 2=8, 解得:t 1=4(不合题意,舍去),t 2=45(不合题意,舍去), ③如图3,当3≤t ≤6时,S =12×6×6﹣12t 2=8,解得:t 1=2√5,t 2=﹣2√5(不合题意,舍去), 综上,t 的值为47√7或2√5时,重叠面积为8.9.等腰△ABC 的直角边AB=BC=10cm ,点P 、Q 分别从A 、C 两点同时出发,均以1cm/秒的相同速度作直线运动,已知P 沿射线AB 运动,Q 沿边BC 的延长线运动,PQ 与直线AC 相交于点D .设P 点运动时间为t ,△PCQ 的面积为S . (1)当点P 运动几秒时,S △PCQ =S △ABC ?(2)作PE ⊥AC 于点E ,当点P 、Q 运动时,线段DE 的长度是否改变?证明你的结论.【解答】(1)由S △ABC =12AB •BC =12×10×10=50.当t <10秒时,P 在线段AB 上,此时CQ=t ,PB=10-t. ∴S △PCQ =12×t×(10−t)=12 (10t −t 2) =50.整理得t 2-10t+100=0无解.当t >10秒时,P 在线段AB 得延长线上,此时CQ=t ,PB=t-10. ∴S △PCQ =12×t×(t −10)=12(t 2−10t) =50.整理得t 2-10t-100=0解得t=5±5√5(舍去负值). ∴当点P 运动5+5√5秒时,S △PCQ =S △ABC .(2)当点P,Q 运动时,线段DE 的长度不会改变. 证明:过Q 作QM ⊥AC ,交直线AC 于点M 易证△APE ≌△QCM ,∴AE=PE=CM=QM=√22t ,∴四边形PEQM 是平行四边形,且DE 是对角线EM 的一半. 又∵EM=AC=10√2,∴DE=5√2.∴当点P 、Q 运动时,线段DE 的长度不会改变. 同理,当点P 在点B 右侧时,DE=5√2。
一元二次方程与动点问题某些动点问题,常可以建立以时间为未知数的一元二次方程模型.通过求解模型,往往会得到两个实数解,这时要根据实际问题作出取舍.既然是动点问题,结果就有多种可能,因此,有时方程模型的两个实数解都是符合题意的,这一点要注意.解决动点问题,我们必须先弄清楚动点是谁?是单动点还是双动点?运动的路径怎样?方向和速度怎样?运动停止的时间怎样?设运动时间为t ,会用t 表示出各个相关的量,找到等量关系并列出关于t 的方程模型.一般情况下,运动路径由几段构成,就需要分几种情况进行讨论,最后做出总结.例1. 如图,在Rt △ABC 中,︒=∠90ACB ,10=AB cm,8=BC cm,点P 从点A 开始沿射线AC 向点C 以2 cm/s 的速度移动,点Q 从点C 开始沿边CB 向点B 以1 cm/s 的速度移动.如果点P 、Q 分别从点A 、C 同时出发,运动的时间为t s,当点Q 运动到点B 时,两点停止运动.(1)当点P 在线段AC 上运动时,P 、C 两点之间的距离为_________cm;(用含t 的代数式表示)(2)在运动的过程中,是否存在某一时刻,使得△PQC 的面积是△ABC 的面积的61若存在,求出t 的值;若不存在,说明理由.分析:(1)由题意可知,t AP 2=cm ,t CQ =cm .由勾股定理求出6=AC cm .所以()t PC 26-=cm ,即P 、C 两点之间的距离为()t 26-cm ;(2)用含t 的代数式表示△PQC 的面积,由ABC PQC S S ∆∆=61建立关于t 的一元二次方程,由方程是否有实数根说明t 的存在性.由于点P 沿射线AC 运动,且运动停止时间为8s,所以需要分两种情况进行讨论:点P 在线段AC 上运动(t <0≤3)和点P 在线段AC 的延长线上运动(t <3≤8).解:(1)()t 26-;(2)由题意可知:t CQ =cm.当t <0≤3时,()t PC 26-=cm.∴()t t t t PC CQ S PQC 32621212+-=-=⋅=∆(cm 2) 由486216161=⨯⨯⨯==∆∆ABC PQC S S 可得: 432=+-t t 即0432=+-t t∵()074432<-=⨯--=∆ ∴该方程无实数根;当t <3≤8时,()t PC 26-=cm.∴()46221=-t t ,即0432=--t t 解之得:1,421-==t t (不符合题意,舍去)综上所述,当4=t 时,△PQC 的面积是△ABC 的面积的61. 例2. 如图,在矩形ABCD 中,5=AB cm,6=BC cm,点P 从点A 开始沿AB 向终点B 以1 cm/s 的速度移动,与此同时,点Q 从点B 开始沿BC 向终点C 以2 cm/s 的速度移动,如果点P 、Q 分别从点A 、B 同时出发,当点Q 运动到点C 时,两点停止运动.设运动的时间为t s.(1)填空:=BQ _________,=PB _________;(用含t 的代数式表示)(2)当t 为何值时,PQ 的长度等于102cm? (3)是否存在t 的值,使得五边形APQCD 的面积等于26 cm 2若存在,请求出此时t 的值;若不存在,请说明理由.解:(1)t 2cm,()t -5cm;(2)在Rt △BPQ 中,由勾股定理得:222PQ PB BQ =+∴()()()22210252=-+t t 解之得:3=t∴当3=t 时,102=PQ cm;(3)3065=⨯=⋅=BC AB S ABCD 矩形 cm 2若五边形APQCD 的面积等于26 cm 2,则4=∆BPQ S cm 2 ∴()45221=-⨯t t ∴4,121==t t (不符合题意,舍去)∴存在1=t ,使得五边形APQCD 的面积等于26 cm 2.例3. 如图,在△ABC 中,︒=∠90B ,6=AB cm,12=BC cm,点P 从点A 开始沿AB 边向点B 以1 cm/s 的速度移动,点Q 从点B 开始沿BC 边向点C 以2 cm/s 的速度移动.(1)如果P 、Q 分别从A 、B 同时出发,几秒钟后△PBQ 的面积等于8 cm 2(2)在(1)中,△PBQ 的面积能否等于10 cm 2说明理由. CA BQP解:(1)设x 秒后△PBQ 的面积等于8 cm 2.由题意可知:x AP =cm,x BQ 2=cm∴()x BP -=6cm∵()86221=-⨯=∆x x S PBQ ∴0862=+-x x解之得:4,221==x x∴2s 或4s 后△PBQ 的面积等于8 cm 2;(2)由题意可得:()106221=-⨯x x ∴01062=+-x x∵()0410462<-=⨯--=∆∴该方程无实数根∴△PBQ 的面积不能等于10 cm 2.。
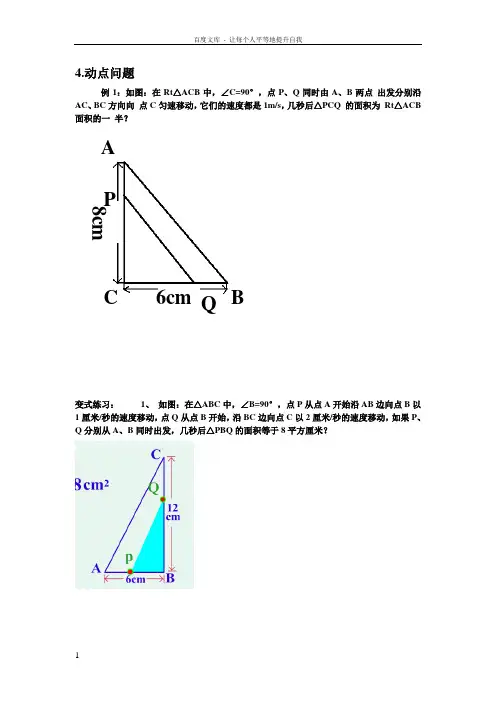
4.动点问题
例1:如图:在Rt △ACB 中,∠C=90°,点P 、Q 同时由A 、B 两点 出发分别沿AC 、
BC 方向向 点C 匀速移动,它们的速度都是1m/s ,几秒后△PCQ 的面积为 Rt △ACB 面积的一 半?
变式练习: 1、 如图:在△ABC 中,∠B=90°,点P 从点A 开始沿AB 边向点B 以1厘米/秒的速度移动,点Q 从点B 开始,沿BC 边向点C 以2厘米/秒的速度移动,如果P 、Q 分别从A 、B 同时出发,几秒后△PBQ 的面积等于8平方厘米?
A
B
C P Q 6cm 8cm
2、如图,在△ABC 中,AB=6cm ,AC=12cm 动点D 从A 点出发到B 点为止,运动的速度为1cm/秒;同时动点E 从C 点出发到A 点为止,点E 运动的速度为2cm/秒那么当点A 、D 、E 为顶点的三角形与△ABC 相似时,运动的时间是( )
3.如图,在矩形ABCD 中,AB=3,BC=4,点P 以每秒2个单位长度的速度从点C
出发,沿CA 向点A 运动;点Q 同时以每秒1个单位长度的速度从点A 出发,沿AB 向点B 运动,设P 、Q 两点移动t 秒
(1)求△APQ 与△ABC 相似时t 的值 B
C
E D A
(2)求四边形BCPQ面积S与时间t的关系式
(3)求△APQ为等腰三角形时t的值
例2:一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正
10
以40海里/时的速度由南向北移动,距台风中心20 海里的圆形区域(包括边界)都属台风区.当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,请说明理由.
变式练习:某军舰以20节的速度由西向东航行,一艘电子侦察船以30节的速度由南向北航行,它能侦察出周围50海里(包括50海里)范围内的目标。
如图,当该军舰行至A处时,电子侦察船正位于A处正南方向的B处,且AB=90海里。
如果军舰和侦察船仍按原速度沿原方向继续航行,那么航行途中侦察船能否侦察到这艘军舰?如果能,最早何时能侦察到?如果不能,请说明理由。