CPK 制作能力数据
- 格式:doc
- 大小:60.00 KB
- 文档页数:2


CPK为什么要定1,1.33,1.67,这几个值?CPK:Complex Process Capability index 的缩写,是现代企业用于表示制程能力的指标。
现今下产品的质量要求越来越高,产品的质量也不是仅仅能保证在公差范围内就能满足要求,因此对产品的质量关注从原来的被动检查产品尺寸转换到对产品加工过程的控制,那么如何来评价某个过程对产品加工质量的控制能力,利用统计学的原理按照一定的时间规律、抽样方案对加工生产出的产品进行数据统计,通过计算其产品数据的离散度、标准差等数据来表达这个过程中产品的质量波动情况,CPK就在这种情况应运而生。
CPK用数值来表示,该值反映的是制造加工过程控制能力的大小,数值越大表示该过程的控制能力越好,产品的一致性越好,产品的尺寸变化波动越小越靠近中间值;而数值越大表示该过程的控制能力越差,产品的一致性越差,产品的尺寸变化波动越大离散度越大,甚至容易超出两边极限公差。
CPK的计算数据由至少125组数据组成,抽取的数据也有一定的要求(每5件为一组连续数据,每组之间按一定的时间间隔进行),抽取数据时制程必须是无任何异常状态下进行,所以CPK值反应的是某个制程在正常工作状态下的过程控制能力。
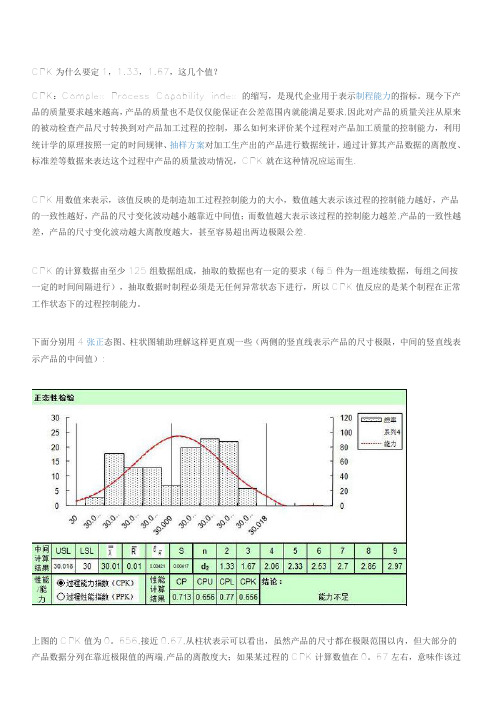
下面分别用4张正态图、柱状图辅助理解这样更直观一些(两侧的竖直线表示产品的尺寸极限,中间的竖直线表示产品的中间值):上图的CPK值为0.656,接近0.67,从柱状表示可以看出,虽然产品的尺寸都在极限范围以内,但大部分的产品数据分列在靠近极限值的两端,产品的离散度大;如果某过程的CPK计算数值在0.67左右,意味作该过程的控制能力并不稳定,具有超出产品极限的风险,如果数值小于0.67,加工过程中可能已经有超差极限值得产品存在。
上图的CPK值为1.078,与CPK值为0.656的图形对比可以看出,产品的尺寸的波动范围比前一副图约小一点,更趋近中间值。
因此当CPK值增大时,该图反应出的过程控制能力就比CPK值为0.656的过程控制能力要好,那么产品超差两端极限的情况也就更小。
CPK为什么要定1,1.33,1.67,这几个值?CPK:Complex Process Capability index 的缩写,是现代企业用于表示制程能力的指标。
现今下产品的质量要求越来越高,产品的质量也不是仅仅能保证在公差范围内就能满足要求,因此对产品的质量关注从原来的被动检查产品尺寸转换到对产品加工过程的控制,那么如何来评价某个过程对产品加工质量的控制能力,利用统计学的原理按照一定的时间规律、抽样方案对加工生产出的产品进行数据统计,通过计算其产品数据的离散度、标准差等数据来表达这个过程中产品的质量波动情况,CPK就在这种情况应运而生.CPK用数值来表示,该值反映的是制造加工过程控制能力的大小,数值越大表示该过程的控制能力越好,产品的一致性越好,产品的尺寸变化波动越小越靠近中间值;而数值越大表示该过程的控制能力越差,产品的一致性越差,产品的尺寸变化波动越大离散度越大,甚至容易超出两边极限公差.CPK的计算数据由至少125组数据组成,抽取的数据也有一定的要求(每5件为一组连续数据,每组之间按一定的时间间隔进行),抽取数据时制程必须是无任何异常状态下进行,所以CPK值反应的是某个制程在正常工作状态下的过程控制能力。
下面分别用4张正态图、柱状图辅助理解这样更直观一些(两侧的竖直线表示产品的尺寸极限,中间的竖直线表示产品的中间值):上图的CPK值为0。
656,接近0.67,从柱状表示可以看出,虽然产品的尺寸都在极限范围以内,但大部分的产品数据分列在靠近极限值的两端,产品的离散度大;如果某过程的CPK计算数值在0。
67左右,意味作该过程的控制能力并不稳定,具有超出产品极限的风险,如果数值小于0.67,加工过程中可能已经有超差极限值得产品存在。
上图的CPK值为1.078,与CPK值为0.656的图形对比可以看出,产品的尺寸的波动范围比前一副图约小一点,更趋近中间值.因此当CPK值增大时,该图反应出的过程控制能力就比CPK值为0。



製程能力指數Ca或k(準確度;Accuracy):表示製程特性中心位置的偏移程度,值等於零,即不偏移。
值越大偏移越大,越小偏移越小。
製程準確度Ca(Caoability of Accuracy)標準公式簡易公式T=USL-LSL=規格上限-規格下限=規格公差P S.單邊規格(設計規格)因沒有規格中心值,故不計算Ca製造規格將單邊規格公差調整為雙邊規格,如此方可計算Ca(Xbar -μ) (實績平均值-規格中心值)Ca(k) =──────=───────────(T /2) (規格公差/2)T=USL-LSL=規格上限-規格下限=規格公差PS.製程特性定義單邊規格(設計規格)因沒有規格中心值,故不計算Ca製造規格將單邊規格公差調整為雙邊規格,如此方可計算Ca當Ca =0 時,代表量測製程之實績平均值與規格中心相同;無偏移當Ca =±1 時,代表量測製程之實績平均值與規格上或下限相同;偏移100%評等參考:Ca值愈小,品質愈佳。
依Ca值大小可分為四級製程精密度Cp(Caoability of Precision)製程能力指數Cp、Pp、CPU、CPL(精密度;Precision):表示製程特性的一致性程度,值越大越集中,越小越分散。
或:雙邊能力指數(長期):雙邊績效指數(短期):單邊上限能力指數:單邊下限能力指數USL:特性值之規格上限;即產品特性大於USL在工程上將造成不合格LSL:特性值之規格下限;即產品特性小於LSL在工程上將造成不合格:製程平均數估計值;即製程目前特性值的中心位置:製程標準差估計值;即製程目前特性值的一致程度PS.製程特性定義單邊規格(設計規格)因沒有規格上限或下限沒有規格下限Cp =CPU =Cpk沒有規格上限Cp =CPL = Cpk綜合製程能力指數Cpk:同時考慮偏移及一致程度。
Cpk=( 1 -k ) xCp 或MIN {CPU,CPL}Ppk=( 1 -k ) xPp 或MIN {PPU,PPL}(X –μ)K=|Ca|=──────(T/2)PS.製程特性定義單邊規格(設計規格)因沒有規格上限或下限沒有規格下限Cp =CPU =Cpk沒有規格上限Cp =CPL =Cpk評等參考當Cpk值愈大,代表製程綜合能力愈好。
工序能力指数CPK的计算和分析CPK的计算公式如下:CPK = min(USL - μ,μ - LSL)/(3 * σ)其中,USL为规格上限,LSL为规格下限,μ为平均值,σ为标准差。
CPK的值越大,表示工序的稳定性和可控性越强。
一般来说,CPK值大于1.33被认为是良好的,大于1.67则被认为是极好的。
而CPK值小于1则表示工序不稳定或者不可控。
CPK的分析可以从以下几个方面进行:1.变异性分析:通过计算标准差和绘制控制图来评估工序的变异性。
如果标准差较小,并且控制图上的数据点在控制界限内,则说明工序具有较小的变异性,可以认为是稳定的。
反之,则说明工序存在较大的变异性,需要进一步改进。
2.规格限值分析:通过比较规格限值和平均值,以及计算CPK值,来评估工序是否能够满足产品的规格要求。
如果CPK值大于1,则说明工序具有足够的能力满足规格要求。
如果CPK值小于1,则需要进行进一步的改进,以提高工序的能力。
3.误差源分析:通过分析工序中可能存在的误差源,找出和改进引起工序不稳定的原因。
误差源可能包括人为因素、设备问题、材料质量等。
通过改进和优化这些误差源,可以提高工序的稳定性和可控性。
4.过程能力改进:通过改进工序中的控制措施和方法,来提高工序的能力。
例如,可以采用六西格玛等质量管理工具,优化工序的流程和参数设定,以减少变异性和提高工序的能力。
总之,CPK是评估工序稳定性和可控性的重要指标,可以通过计算和分析CPK值来评估工序的能力,并通过改进控制措施和优化过程来提高工序的能力。
1、何谓CPK?制程能力指数﹝Process capability index─传统上简称为Cp﹞,系统计制程管制SPC的一个很重要的指标。
代表着我们产品制程的质量有多好或不良率是多少。
自从1950年代SPC普及以来,大抵使用Cp这样的一个能力指数来反映质量水平的状况。
但随着时间的推移,电子产业的兴起,以前的质量水平不良率以百分比%为单位就足以胜任,因为电子组件的数量庞大,百分比的不良率不敷使用,所以演化成以PPM为不良率的单位。
同时更自1980年代因为美国的汽车产业也不堪日本汽车业的竞争,从而将制程能力指数修正成Cpk,近年来电子产业多以追求Cpk为准。
传统品管上针对这个问题是以Ca处理,但通常都带过未加以刻意强调。
而时下流行的Cpk只是对旧有的Cp做了中心值的修正。
需要注意的是传统上Cp时代,我们对制程能力指数的要求Cp=1,易言之,良品率是99.73%,而多年前Cpk出现时要求的是Cpk=1.33,而这两年则要求提升到Cpk=1.67。
而当Cpk=1.63时即可进入个位数的PPM世界。
2、CPK应用检查重点一般来说,当量测数据收集到之后,就需要将这笔数据的制程平均值μ以及制程变异数σ两个值画在图表上。
当图表画好后,就可以将这些数值与规格界限作比较。
我们知道,大约有68.26%的量测数据会落在平均值上下一个σ之内,大约95.44%的数据会落在平均值上下二个σ之内,大约99.73%的制程数据则会落在平均值上下3个σ之内(见Figure 4.),制程能力的观念就是将自然变异(6σ)与规格公差(USL-LSL)作比较。
制程能力是由以下三个主要因素构成:设计的公差(The Design Specification)制程中心(Mean,μ)变异的大小(Sigma,σ)制程能力指数,Cp,就是将上下规格界限的差异(USL-LSL)与制程变异 (6σ)作比较。
99.7%的数据会落在 3个标准偏差之内。
我们以Push Pull为例(见Figure 5),其制程能力指数,Cp,的记算方式如下:C=(USL-LSL)/6σp从图上可看出上规格界限(USL)为0.07,下规格界限(LSL)为0.04,母体标准偏差为0.005。
制程能力指数cpk计算制程能力指数(Cpk)是一种用于评估制程稳定性和一致性的统计指标。
它是对制程过程的潜在变异性和规格限制之间的差异进行量化的方法。
Cpk值越高,说明制程过程越稳定,产品一致性越好,同时也意味着该制程过程满足规格限制的能力更强。
Cpk值的计算需要依赖制程数据,包括过程的上限规格(USL)、下限规格(LSL)以及制程的标准差(σ)。
根据统计学原理,Cpk的计算公式如下:Cpk = min((USL-μ)/(3σ), (μ-LSL)/(3σ))其中,μ表示过程的平均值。
Cpk值大于1表示制程能力良好,能满足规格要求。
Cpk值越接近于1.33,说明制程过程的能力越高。
制程能力指数的计算过程可以分为以下几个步骤:1. 收集制程数据:首先需要收集一定数量的制程数据,包括产品尺寸、重量、颜色等相关参数。
这些数据应该是随机采样得到的,以确保数据的代表性和可靠性。
2. 计算过程的平均值和标准差:根据收集到的数据,计算出制程过程的平均值和标准差。
平均值表示制程过程的中心位置,标准差表示制程过程的变异程度。
3. 确定规格限制:根据产品设计要求和市场需求,确定制程过程的上限规格和下限规格。
规格限制是产品质量的要求,制程过程必须在规格限制范围内才能被接受。
4. 计算Cpk值:根据上述公式,将制程过程的平均值、标准差和规格限制代入计算,得到Cpk值。
如果Cpk值大于1,说明制程能力良好;如果Cpk值小于1,说明制程能力不足,需要采取改进措施提高制程稳定性和一致性。
Cpk值的计算和评估可以帮助企业了解制程过程的稳定性和一致性,从而及时发现和解决潜在问题,提高产品质量和客户满意度。
对于制造型企业来说,制程能力指数是衡量生产能力和质量水平的重要指标之一。
除了Cpk值,还有其他一些与制程能力相关的指标,如Cp值、Ppk 值等。
Cp值是用于评估制程过程稳定性的指标,它只考虑了过程的平均值和标准差,而没有考虑规格限制。
CPK ——过程能力指数
CP(或CPK)是英文Process Capability index缩写,汉语译作工序能力指数,也有译作工艺能力指数过程能力指数。
工序能力指数,是指工序在一定时间里,处于控制状态(稳定状态)下的实际加工能力。
它是工序固有的能力,或者说它是工序保证质量的能力。
对于任何生产过程,产品质量总是分散地存在着。
若工序能力越高,则产品质量特性值的分散就会越小;若工序能力越低,则产品质量特性值的分散就会越大。
工序能力是表示生产过程客观存在着分散的一个参数。
但是这个参数能否满足产品的技术要求,仅从它本身还难以看出。
因此,还需要另一个参数来反映工序能力满足产品技术要求(公差、规格等质量标准)的程度。
这个参数就叫做工序能力指数。
它是技术要求和工序能力的比值,即工序能力指数=技术要求/工序能力当分布中心与公差中心重合时,工序能力指数记为Cp。
当分布中心与公差中心有偏离时,工序能力指数记为CPK。
运用工序能力指数,可以帮助我们掌握生产过程的质量水平。
工序的质量水平按Cp值可划分为五个等级。
A++级Cpk≥2.0 特优可考虑成本的降低
A+ 级2.0 >Cpk ≥ 1.67 优应当保持之
A 级1.67 >Cpk ≥ 1.33 良能力良好,状态稳定,但应尽力提升为A+级
B 级1.33 >Cpk ≥ 1.0 一般状态一般,制程因素稍有变异即有产生不良的危险,应利用各种资源及方法将其提升为A级
C 级1.0 >Cpk ≥ 0.67 差制程不良较多,必须提升其能力
D 级0.67 >Cpk 不可接受其能力太差,应考虑重新整改设计制程。
★表(-):关键质量特性
★表(二):重要质量特性
★表(三):一般质量特性
★过程能力与不合格率之间的对应关系。