个三角形相似
•角角边定理 •边边边公理 •斜边、直角 边公理
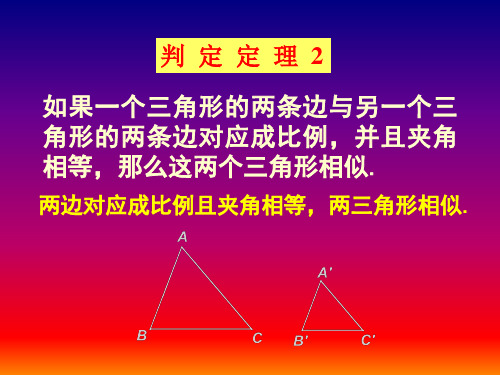
•两 边 对 应 成 比 例 且 夹角相等,两三角 形相似.
•三边对应成比例, 两三角形相似.
例1:根据下列条件,判定△ABC和△A´B´C´
是否相似,并说明理由.
•∠A=120°,AB=7厘米,AC=14厘米,
∠A´=120°,A´B´=3厘米,A´C´=6厘米;
图
的判定方法 的判定方法
形
•定义 •边角边公理 •角边角公理
•定义 •定理 •两角对应相等,两
个三角形相似
•角角边定理 •边边边公理 •斜边、直角
•两 边 对 应 成 比 例 且 夹角相等,两三角 形相似.
边公理
全等三角形 相似三角形
图
的判定方法 的判定方法
形
•定义 •边角边公理 •角边角公理
•定义 •定理 •两角对应相等,两
挑战自我
三个边长为a的正方形ABEG、GEFH 和HFCD,矩形对角线AC的长是 ;
已知:如图,四边形ABEG 、GEFH 、 HFCD都是边长为a的正方形. 求证:△AEF∽△CEA.
证法1:∵正方形ABEG的边长为a,
证法1:∵正方形ABEG的边长为a, ∴AE= a .
证法1:∵正方形ABEG的边长为a, ∴AE= a . 在△AEF和△CEA中, AE∶EF= a∶a= . EC∶EA=2a∶ a= .
证法2:根据题意,可得 AE= a ,AF= a , AC= a . 在△AEF和△CEA中, AE∶EF= a∶a= , EC∶EA=2a∶ a= , CA∶AF = a∶ a= , ∴AE∶EF= EC∶EA= CA∶AF.
证法2:根据题意,可得 AE= a ,AF= a , AC= a . 在△AEF和△CEA中, AE∶EF= a∶a= , EC∶EA=2a∶ a= ,