循环结构、程序框图的画法

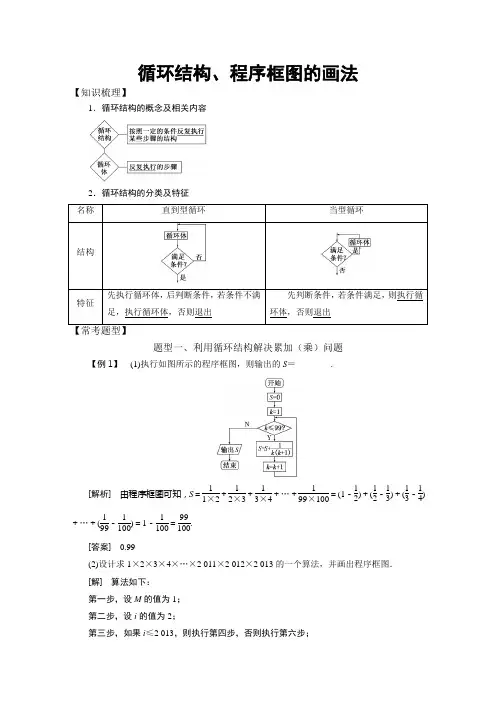
循环结构、程序框图的画法【知识梳理】1．循环结构的概念及相关内容2．循环结构的分类及特征题型一、利用循环结构解决累加（乘）问题【例1】 (1)执行如图所示的程序框图，则输出的S ＝________.[解析] 由程序框图可知，S ＝11×2＋12×3＋13×4＋…＋199×100＝(1－12)＋(12－13)＋(13－14)＋…＋(199－1100)＝1－1100＝99100.[答案] 0.99(2)设计求1×2×3×4×…×2 011×2 012×2 013的一个算法，并画出程序框图． [解] 算法如下： 第一步，设M 的值为1； 第二步，设i 的值为2；第三步，如果i ≤2 013，则执行第四步，否则执行第六步；第四步，计算M乘i并将结果赋给M；第五步，计算i加1并将结果赋给i，返回执行第三步；第六步，输出M的值并结束算法．程序框图如图：【类题通法】利用循环结构应注意的问题(1)如果算法问题里涉及的运算进行多次重复的操作，且先后参与运算的各数之间有相同的变化规律，就可以引入循环变量参与运算，构成循环结构．(2)在循环结构中，要注意根据条件设置合理的计数变量，累加(乘)变量，同时条件的表述要恰当，精确．(3)累加变量的初值一般为0，而累乘变量的初值一般为1，累加(乘)和计数一般是同步进行的，累加(乘)一次，计数一次．【对点训练】编写一个计算12＋32＋52＋…＋9992的算法，并画出程序框图．解：据题意算法如下：第一步，使S＝0；第二步，使i＝1；第三步，使S＝S＋i2；第四步，使i＝i＋2；第五步，如果i＞1 000，则执行第六步，否则返回第三步；第六步，输出S.程序框图如右图：题型二、利用循环结构求满足条件的最值问题【例2】 求满足1＋12＋13＋14＋…＋1n ＞2的最小正整数n ，写出算法，并画出程序框图．[解] 算法：第一步，S ＝0.第二步，i ＝1.第三步，S ＝S ＋1i .第四步，i ＝i ＋1.第五步，若S ≤2，则返回第三步；否则输出i －1，循环结束．程序框图如图．【类题通法】求满足条件的最值问题的实质及注意事项(1)实质：利用计算机的快速运算功能，对所有满足条件的变量逐一测试，直到产生第一个不满足条件的值时结束循环．(2)注意事项：①要明确数字的结构特征，决定循环的终止条件与数的结构特征的关系及循环次数． ②要注意要统计的数出现的次数与循环次数的区别．③要特别注意判断框中循环变量的取值限止，是“＞”“＜”还是“≥”“≤”，它们的意义是不同的．【对点训练】某程序框图如图所示，则该程序的算法功能是________．解析：由程序框图可知，输出的i是满足1×3×5×7×…×n＞50 000的最小正整数n.答案：求满足1×3×5×7×…×n＞50 000的最小正整数n.题型三、循环结构的实际应用【例3】(1)某店一个月的收入和支出总共记录了N个数据，a1，a2，…，a N，其中收入记为正数，支出记为负数．该店用如图所示的程序框图计算月总收入S和月净盈利V，那么在图中空白的判断框和处理框中，应分别填入下列四个选项中的()A．A＞0？，V＝S－T B．A＜0？，V＝S－TC．A＞0？，V＝S＋T D．A＜0？，V＝S＋T[解析]由程序框图可以看出，判断框中应填A＞0？，因为当满足条件时右边执行S＝S ＋A，即收入，故应填A＞0？.而处理框中应填V＝S＋T，因为T为负数即支出，所以V＝S＋T，即收入减去支出．[答案] C(2)某工厂2010年生产轿车20万辆，技术革新后预计每年的产量比上一年增加5%，问最早哪一年生产的轿车超过30万辆？试设计算法并画出相应的程序框图．[解]算法如下：第一步，n＝2010；第二步，a＝20；第三步，T＝0.05a；第四步，a＝a＋T；第五步，n＝n＋1；第六步，若a＞30，输出n，否则执行第三步．程序框图如图所示．【类题通法】利用循环结构解决应用问题的方法【对点训练】某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表所示：如图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，则图中判断框应填________，输出的S＝________.解析：题干中是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，故图中判断框应填i≤6？，输出的S＝a1＋a2＋…＋a6.答案：i≤6？a1＋a2＋…＋a6【练习反馈】1．下列框图是循环结构的是()A．①②B．②③C．③④D．②④解析：选C由循环结构的特点知③④是循环结构，其中①是顺序结构，②是条件结构．2．执行图所示的程序框图，若输出的b的值为16，则图中判断框内①处应填()A．3 B．4C．5 D．12解析：选A按照程序框图依次执行：初始a＝1，b＝1；第一次循环后，b＝21＝2，a＝1＋1＝2；第二次循环后，b＝22＝4，a＝2＋1＝3；第三次循环后，b＝24＝16，a＝3＋1＝4，而此时应输出b的值，故判断框中的条件应为“a≤3？”．3．运行如图程序框图，输出的结果为________．解析：n＝1，S＝1＋0＝1；n＝2，S＝3；n＝3，S＝6；n＝4，S＝10；n＝5，S＝15；n＝6，S＝21；n＝7，S＝28.答案：284．按下列程序框图运算：规定：程序运行到“判断结果是否大于244”为1次运算，若x ＝5，则运算进行________次才停止．解析：第一次运算得13，第二次运算得37，第三次运算得109，第四次运算得325，大于244，程序终止，故运算进行4次．答案：45．画出计算1＋13＋15＋…＋1999的值的一个程序框图．解：程序框图如图所示：。

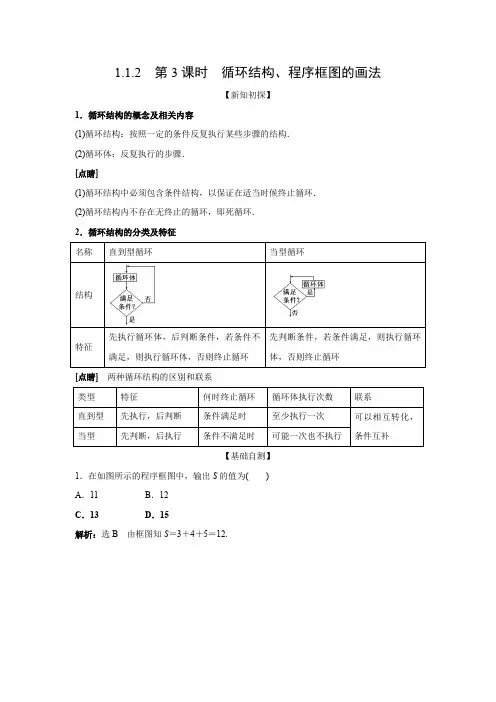
1.1.2 第3课时循环结构、程序框图的画法【新知初探】1．循环结构的概念及相关内容(1)循环结构：按照一定的条件反复执行某些步骤的结构．(2)循环体：反复执行的步骤．[点睛](1)循环结构中必须包含条件结构，以保证在适当时候终止循环．(2)循环结构内不存在无终止的循环，即死循环．2．循环结构的分类及特征名称直到型循环当型循环结构特征先执行循环体，后判断条件，若条件不满足，则执行循环体，否则终止循环先判断条件，若条件满足，则执行循环体，否则终止循环[点睛]两种循环结构的区别和联系类型特征何时终止循环循环体执行次数联系直到型先执行，后判断条件满足时至少执行一次可以相互转化，条件互补当型先判断，后执行条件不满足时可能一次也不执行【基础自测】1．在如图所示的程序框图中，输出S的值为()A．11B．12C．13 D．15解析：选B由框图知S＝3＋4＋5＝12.第1题图第2题图2．程序框图如图所示，其输出结果是()A．110 B．118C．127 D．132解析：选C由题图可知，a的值依次为1,3,7,15,31,63,127，因为127>100，所以输出a＝127. 3．如图所示的程序框图运行后，输出的结果为________．解析：由题意知，s＝1×5×4＝20.答案：204．一个算法的程序框图如图所示，若该程序输出的结果为56，则判断框①中应填入的是________．解析：由框图知，56＝11×2＋12×3＋13×4＋…＋1n n ＋1＝1－1n ＋1，∴n ＝5，运行5次．∴判断框中应为“i ≤5？”． 答案：5【题型探究】题型一含循环结构程序框图的设计[典例] 设计一个计算1×3×5×…×99的算法，画出程序框图． [解] 算法如下： 第一步，令i ＝1，S ＝1. 第二步，S ＝S ×i . 第三步，i ＝i ＋2.第四步，判断i >99是否成立，若成立，则输出S ；否则执行第二步． 程序框图如图所示：【规律方法】利用循环结构解决问题的“三个确定”(1)确定循环变量及初始值，弄清循环变量表示的意义、取值范围及变化规律． (2)确定循环体的功能，根据实际情况确定采用哪种循环结构． (3)确定循环结构的终止条件，弄清不等号的方向及是否含有等号．【跟踪训练】如图是求的值的程序框图，则判断框中应填入的为________．解析：i ＝1时，得到A ＝12＋12，共需加5次，故i ≤5.答案：5题型二利用循环结构求满足条件的最值问题[典例] 设计一个程序框图，求满足1＋2＋3＋…＋n >2 016的最小正整数n . [解] 程序框图如图所示：【规律方法】求满足条件的最值问题的实质及注意事项(1)实质：利用计算机的快速运算功能，对所有满足条件的变量逐一测试，直到产生第一个不满足条件的值时结束循环． (2)注意事项：①要明确数字的结构特征，决定循环的终止条件与数的结构特征的关系及循环次数． ②要注意要统计的数出现的次数与循环次数的区别．③要特别注意判断框中循环变量的取值限制，是“＞”“＜”还是“≥”“≤”，它们的意义是不同的． 【跟踪训练】某程序框图如图所示，则该程序的算法功能是________．解析：由程序框图可知，输出的i 是满足1×3×5×7×…×n ＞50 000的最小正整数n . 答案：求满足1×3×5×7×…×n ＞50 000的最小正整数n题型三循环结构的实际应用[典例] (1)某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，根据如图所示的程序框图，若其中4位居民的月均用水量(单位：吨)分别为1,1.5,1.5,2，则输出的结果s 为________．(2)某商场第一年销售计算机5 000台，如果平均每年销售量比上一年增加10%，那么从第一年起，大约几年可使总销售量达40 000台？画出解决此问题的程序框图． [解析] (1)第一步，s 1＝s 1＋x 1＝0＋1＝1，s ＝1，i ＝2； 第二步，s 1＝s 1＋x 2＝1＋1.5＝2.5，s ＝2.52，i ＝3；第三步，s 1＝s 1＋x 3＝2.5＋1.5＝4，s ＝43，i ＝4；第四步，s 1＝s 1＋x 4＝4＋2＝6，s ＝14×6＝32，i ＝5，不满足i ≤4，输出s ＝32. 答案：32(2)解：程序框图如图所示：【规律方法】利用循环结构解决应用问题的方法【跟踪训练】上海浦东新区2008年的生产总值约为3 151亿元人民币，如果从此浦东新区生产总值的年增长率为10.5%，求浦东新区最早哪一年的生产总值超过8 000亿元人民币？某同学为解答这个问题设计了一个程序框图，但不慎将此框图的一个处理框中的内容污染而看不到了，则此框图中因被污染而看不到的内容应是( )A．a＝a＋b B．a＝a×bC．a＝(a＋b)n D．a＝a×b n解析：选B根据题意，本程序框图意义为计算生产总值．由题意知，a＝3 151，b＝1.105，n＝2 008，当满足a>8 000时，跳出循环，输出年份n.当不满足a>8 000时，执行语句n＝n＋1.根据已知，a为2008年生产总值，b为“1＋增长率”，故执行的语句应为a＝a×b，故选B.。

第3课时循环结构、程序框图的画法【学习目标】1．掌握两种循环结构的程序框图的画法．2．能进行两种循环结构的程序框图的转化．3．能正确设计程序框图解决有关实际问题．【核心内容】1．用框图表示算法的循环结构．(重点)2．利用循环结构解决实际问题．(难点)3．程序框图是本节课的重点，高考多以选择题或填空题的形式出现．自学导引1．循环结构的概念在一些算法中，经常会出现从某处开始，按照一定的条件反复执行某些步骤的情况，这就是循环结构．反复执行的步骤称为循环体．2．常见的两种循环结构名称结构图特征直到型循环结构在执行了一次循环体后，对条件进行判断，如果条件不满足，就继续执行循环体，直到条件满足时终止循环．因此，这种循环结构称为直到型循环结构．当型循环结构在每次执行循环体前，对条件进行判断，当条件满足时，执行循环体，否则终止循环．因此，这种循环结构称为当型循环结构.问题1：循环结构中判断框中的条件是唯一的吗？3．程序框图的画法及步骤(1)在用自然语言表述一个算法后，可以画出程序框图，用顺序结构、条件结构和循环结构来表示这个算法．这样表示的算法清楚、简练，便于阅读和交流．(2)设计一个算法的程序框图的一般步骤：①用自然语言表述算法步骤；②确定每一个算法步骤所包含的逻辑结构，并用相应的程序框图表示，得到表示该步骤的程序框图；③将所有步骤的程序框图用流程线连接起来，并加上终端框，得到表示整个算法的程序框图．名师点睛1．画循环结构程序框图的三要素利用循环结构表示算法时，在画算法的框图之前就应该分析清楚循环结构的三要素：循环变量、循环体、循环终止条件，只有准确地把握了这三个要素，才能清楚地画出循环结构的程序框图．(1)循环变量：一般分为累计变量和计数变量，应明确它的初始值、步长(指循环变量每次增加的量)、终值．(2)循环体：也称循环表达式，它是算法中反复执行的部分．(3)循环的中止条件：程序框图中用一个判断框来表示，用它判断是否继续执行循环体．2．当型循环结构与直到型循环结构的联系和区别(1)联系①当型循环结构与直到型循环结构可以相互转化；②循环结构中必然包含条件结构，以保证在适当的时候终止循环；③循环结构只有一个入口和一个出口；④循环结构内不存在死循环，即不存在无终止的循环．(2)区别直到型循环结构是先执行一次循环体，然后再判断是否继续执行循环体，当型循环结构是先判断是否执行循环体；直到型循环结构是在条件不满足时执行循环体，当型循环结构是在条件满足时执行循环体．要掌握这两种循环结构，必须抓住它们的区别．3．计数变量与累计变量的有关理解一般地，循环结构中都有一个计数变量和累加变量：计数变量用于记录循环次数，同时它的取值还用于判断循环是否终止；累加变量用于表示每一步的计算结果．计数变量和累加变量一般是同步执行的，累加一次，计数一次．①变量i是一个计数变量，它可以统计执行的循环次数，它控制着循环的开始和结束；算法在执行循环结构时，就赋予计数变量初始值，预示循环的开始，每执行一次循环结构，计数变量的值就发生变化，并在每一次重复执行完循环体时或重新开始执行循环体时，要判断循环体的条件是否已达到终止循环的要求．②变量S是一个累加变量，它是我们编写算法中至关重要的量，我们根据要求制定它的变化情况，通常情况下与计数变量有相应关系．每执行一次循环结构，累加变量的值就发生一次变化，并在每一次重复执行完循环体时或重新开始执行循环体时，观察累加变量值的情况，并根据题意对累加变量的要求设置循环结构、终止循环的条件．例题探究题型一用循环结构解决累加、累乘问题【例1】设计求1＋3＋5＋7＋…＋31的算法，并画出相应的程序框图．【变式1】设计求1×2×3×4×…×2 009×2 010的算法，并画出程序框图．题型二利用循环结构寻找特定的数【例2】写出求1＋2＋3＋…＋n＞20 000的最小正整数n的算法，并画出相应的算法框图．【变式2】设计求使1＋2＋3＋4＋5＋…＋n ＜100成立的最大自然数n 的值的算法，画出程序框图．题型三 循环结构程序框图的识别与解读【例3】 (1)某程序框图如图(1)所示，该程序运行后输出的k 的值是( )．A ．4B ．5C ．6D ．7(2)如图(2)是一个算法的程序框图，该算法所输出的结果是( )．A.12B.23C.34D.45【变式3】如果执行下面的程序框图，那么输出的S为________．题型四循环结构的实际应用【例4】某工厂2012年生产小轿车200万辆，技术革新后预计每年的生产能力比上一年增加5%，问最早哪一年该厂生产的小轿车数量超过300万辆？写出解决该问题的一个算法，并画出相应的程序框图．【变式4】某班共有学生50人．在一次数学测试中，要搜索出测试中及格(60分以上)的成绩，试设计一个算法，并画出程序框图．当堂检测1．某同学设计的程序框图如图所示，用以计算和式12＋22＋32＋…＋202的值，则在判断框中应填写()A．i≤19 B．i≥19C．i＞21 D．i＜21(第1题图)2．如图所示，程序框图中输出S的值为__________．(第2题图)3．已知程序框图如下图所示，则输出的a的值为__________．(第3题图)4．某程序框图如图所示，则输出的S ＝__________.(第4题图)5．画出计算1＋12＋13＋…＋1999的值的一个程序框图．参考答案问题1：提示 不是．在具体的程序框图设计时，这里的条件可以不同，但不同表示应该有共同的确定的结果． 【例1】解：第一步：S ＝0.第二步：i ＝1. 第三步：S ＝S ＋i . 第四步：i ＝i ＋2.第五步：若i 不大于31，返回执行第三步，否则执行第六步； 第六步：输出S 值．程序框图如图：【变式1】解：算法如下：第一步，设M的值为1.第二步，设i的值为2.第三步，如果i≤2 010，则执行第四步，否则转去执行第六步．第四步，计算M乘i，并将结果赋给M.第五步，计算i加1并将结果赋给i，转去执行第三步．第六步，输出M的值并结束算法．程序框图如图：【例2】解：法一算法为：第一步，令n＝0，S＝0.第二步，n＝n＋1.第三步，S＝S＋n.第四步，如果S＞20 000，则输出n，否则，执行第二步．该算法的框图如图所示：法二第一步：取n的值等于1.第二步：计算n （n ＋1）2.第三步：如果n （n ＋1）2的值大于10 000，那么n 即为所求；否则，让n 的值增加1，然后返回第二步重复操作．根据以上步骤，可以画如图所示的程序框图．【变式2】解：算法为：第一步，令S ＝0，n ＝1. 第二步，S ＝S ＋n . 第三步，n ＝n ＋1.第四步，若S ≥100，则输出n －2；否则，返回第二步． 程序框图如图所示：【例3】【解析】(1)当k ＝0时，S ＝0S ＝1k ＝1，当S ＝1时，S ＝1＋21＝3k ＝2， 当S ＝3时，S ＝3＋23＝11＜100k ＝3， 当S ＝11时，k ＝4，S ＝11＋211＞100，故k ＝4.(2)运行第一次的结果为n ＝0＋11×2＝12；第二次n ＝12＋12×3＝23；第三次n ＝23＋13×4＝34.此时i ＝4程序终止， 即输出n ＝34.【答案】 (1)A (2)C【变式3】【解析】 当k ＝1，S ＝0＋2×1；当k ＝2，S ＝0＋2×1＋2×2； 当k ＝3，S ＝0＋2×1＋2×2＋2×3； …当k ＝50，S ＝0＋2×1＋2×2＋2×3＋…＋2×50＝2 550. 【答案】2 550 【例4】算法如下：第一步，令n ＝0，a ＝200，r ＝0.05. 第二步，T ＝ar (计算年增量)． 第三步，a ＝a ＋T (计算年产量)． 第四步，如果a ≤300，那么n ＝n ＋1， 返回第二步；否则执行第五步． 第五步，N ＝2 012＋n . 第六步，输出N . 程序框图如图所示：【变式4】解：算法步骤如下：第一步，把计数变量n的初始值设为1.第二步，输入一个成绩r，比较r与60的大小．若r≥60，则输出r，然后执行下一步；若r<60，则执行下一步．第三步，使计数变量n的值增加1.第四步，判断计数变量n与学生个数50的大小，若n≤50，返回第二步，若n>50，则结束．程序框图如图：1．【解析】该程序框图中含有当型循环结构，判断框内的条件不成立时循环终止．由于是当i＝21时开始终止循环，则在判断框中应填写i＜21.【答案】D2．【解析】该程序框图的运行过程是：i＝1，S＝1i＝1＋1＝2S＝2×(1＋1)＝4 i＝2＞5不成立i＝2＋1＝3S＝2×(4＋1)＝10 i＝3＞5不成立i＝3＋1＝4S＝2×(10＋1)＝22 i＝4＞5不成立i＝4＋1＝5S＝2×(22＋1)＝46 i＝5＞5不成立i＝5＋1＝6S＝2×(46＋1)＝94 i＝6＞5成立输出S＝94.【答案】943．【解析】把每次得到的a依次记作a n，则a1＝2，a2＝12，a3＝-1，a4＝2，…是以3为周期的数列．最后一个得到的为a2 013，又a2 013＝a3×671＝a3＝-1.【答案】-14．【答案】265．解：程序框图如下：方法一：当型循环结构方法二：直到型循环结构。