河海大学结构可靠度作业

可靠度作业参考答案可靠度作业参考答案在工程学和科学领域中，可靠度是一个非常重要的概念。

它指的是一个系统、设备或者过程在一定时间内正常运行的概率。

可靠度的计算和评估对于确保系统的稳定性和可持续性至关重要。

本文将介绍可靠度的基本概念和计算方法，并提供一些可靠度作业的参考答案。

一、可靠度的基本概念可靠度是指在特定条件下，系统或者设备在一定时间内正常运行的概率。

它是一个非常重要的指标，可以用来评估系统的稳定性和可持续性。

可靠度的计算通常基于失效率和故障率，其中失效率指的是单位时间内失效的概率，故障率指的是单位时间内发生故障的概率。

二、可靠度的计算方法1. 失效率的计算失效率可以通过以下公式计算：失效率 = 失效数 / 运行时间其中，失效数指的是在给定时间内发生的失效次数，运行时间指的是系统或设备正常运行的时间。

2. 故障率的计算故障率可以通过以下公式计算：故障率 = 故障数 / 运行时间其中，故障数指的是在给定时间内发生的故障次数，运行时间指的是系统或设备正常运行的时间。

3. 可靠度的计算可靠度可以通过以下公式计算：可靠度 = 1 - 故障率可靠度的取值范围在0到1之间，1表示系统完全可靠，0表示系统完全不可靠。

三、可靠度作业参考答案以下是一些可靠度作业的参考答案：1. 问题：一个设备在1000小时内发生了10次故障，计算该设备的故障率和可靠度。

解答：故障率 = 10 / 1000 = 0.01，可靠度 = 1 - 0.01 = 0.99。

2. 问题：一个系统在5000小时内正常运行，没有发生任何故障，计算该系统的失效率和可靠度。

解答：失效率 = 0 / 5000 = 0，可靠度 = 1 - 0 = 1。

3. 问题：一个设备在2000小时内发生了5次故障，计算该设备的故障率和可靠度。

解答：故障率 = 5 / 2000 = 0.0025，可靠度 = 1 - 0.0025 = 0.9975。

通过以上的计算，我们可以得出不同设备和系统的可靠度指标。

2010-2011学年第一学期《钢筋混凝土基本理论》期中试卷（土木工程及土木基地2008级）姓名 班级 学号 成绩 一、单项选择题（每题2分，共20分）1、某强度等级混凝土下列强度指标中，（B ）强度最大。

A ． f c B ． f cuk C ． f t D ．f ck2、与素混凝土梁相比，钢筋混凝土梁抵抗开裂的能力（B ）。

A ．提高许多 B ．提高不多 C ．完全相同 D ．不确定3、若工程结构构件超过其正常使用极限状态，则其丧失了（C ）。

A ．安全性或适用性 B ．安全性或经济性 C ．适用性或耐久性 D ．经济性或耐久性4、结构可靠指标β增大时，其失效概率p f 将（C ）。

A ．增大B ．不变C ．减小D ．可能增大，也可能减小 5、（A ）是计算受弯构件开裂弯矩的依据。

A ．Ⅰa 阶段B ． Ⅱa 阶段C ．Ⅲa 阶段D ．第Ⅱ阶段 6、对于双筋矩形截面梁，计算得到'2s a x <，则（B ）。

A ．该梁为超筋梁B ．破坏时受压区钢筋不能屈服C ．该梁为少筋梁D ．破坏时受拉区钢筋不能屈服7、对同一受弯构件，不配置腹筋，其斜截面可能发生斜压、剪压和斜拉破坏。

这三种破坏时承载力大小关系为（D ）。

A ．斜拉>斜压>剪压B ．剪压>斜压>斜拉C ．斜压>斜拉>剪压D ．斜压>剪压>斜拉8、厚腹梁进行斜截面抗剪设计时，应满足V ≤0.25βc f c bh 0，其目的是为了防止发生（C ）破坏。

A ．斜拉破坏B ．剪压破坏C ．斜压破坏D ．少筋破坏 9、双筋梁截面设计时，A s 和A s ＇均未知，这时补充条件（A ）。

A ．b ξξ=B ．s a x '2=C ．A s =A s ＇D ．bh A s min ρ=10、受弯构件正截面受弯承载力图包住设计弯矩图，可以保证（C）。

A．斜截面受剪承载力B．斜截面受弯承载力C．正截面受弯承载力D．正截面受弯承载力和斜截面受弯承载力二、判断题，如是错误的，需给出正确答案（每题3分，共15分）1、混凝土的变形随荷载增大而增大的现象称为徐变。

共 1 页第 1 页1．结构可靠性的指标有哪些?结构可靠性是结构的强度，稳定即所谓安全性，结构的适用性,结构的耐久性的总称。

结构的安全性是指(1)结构能承受在正常施工和正常使用时，可能出现的各种作用。

（2）结构在偶然事件发生时及发生后，仍能保持必需的整体稳定性;结构的适用性是指在正常使用时，具有良好的工作性能;结构的耐久性是指在正常维修和保护下，具有良好的耐久性能。

具体到已进入实用阶段的近似概率模式有失效概率P f 和可靠指标β.2．试比较定值设计方法和概率设计方法的不同和特点。

定值设计法将有关参数看成是不变的定值，并主要在经验的基础上确定设计安全因数，由于采用的荷载和材料强度设计取值的原则不同,安全因数并不能从定量上度量结构的可靠度。

概率设计法是将作用荷载和抗力都看成是随即变量，并用失效概率或可靠指标来度量结构的可靠程度。

这种方法以承认结构有失效的可能性为前提，从抗力大于荷载的概率出发进行可靠度设计的，而不是用一个笼统的安全因数。

它比定值法更能揭示结构失效的成因，在观念上更容易为人们所接受.结构绝对安全是不可能的,这样的设计目的也不必要。

结构设计的主要目的是在可接受的概率水平上保证结构在规定设计使用期满足预期的用途。

3．随机变量有哪几种常见的分布函数？（1）二项式分布;X 在n 次试验中,事件A 出现k 次的概率为：P （X=k)=C n k p k q n-k (n!p k q n-k ）/ k ！(n —k)!（2）均匀分布()⎪⎩⎪⎨⎧≤≤-=其它012112x x x x x x f（3)普阿松分布 ()k k k n k k n e k q p C n m i l k X P --=∞→==!λ（4)正态分布；密度函数为 ()()22221xx x e x x f σμπσ--=（5）极值分布()()()u x e u x e x f -----=ααα（6)皮尔逊曲线族;将()积分2210x a x a a y d x x d y d +++=（7）对数正态分布;密度函数为()()⎥⎥⎦⎤⎢⎢⎣⎡--=222exp 21y y y y u y e y f σπσ (8) 2分布 ()()02212122≥⎪⎭⎫ ⎝⎛Γ=--x e x x f x γγγ4．工程结构动力可靠性研究还有哪些进一步的问题?(1）工程结构的动力可靠性分析，应综合考虑各种因素，如与抗震结构有关的地震危险性分析中的诸因素，以及结构使用年限，使用条件及其随机变化，各种随机荷载的发生概率及其组合，结构的刚度,质量，强度等的随机性。

模拟试卷一一、选择题（每题2分，共30分）1.摩擦型高强螺栓连接与承压型高强螺栓连接的主要区别是。

(A)摩擦面处理不同(B)材料不同(C)预拉力不同(D)设计计算时所取极限状态不同2.在静力荷载作用下，钢材承受三向拉应力时，易发生。

(A)塑性破坏(B)脆性破坏(C)疲劳破坏(D)无法判定3.进行强度验算时，荷载应采用。

(A)将永久荷载的标准值乘以永久荷载分项系数(B)将可变荷载的标准值乘以可变荷载分项系数(C)永久荷载和可变荷载的标准值，均不乘以各自的分项系数(D)将永久荷载和可变荷载的标准值均乘以各自的分项系数4.钢结构焊接节点设计中，应尽可能选用的焊接位置。

(A)俯焊(B)仰焊(C)立焊(D)任意5.在缀条稳定验算式中，系数是。

(A)考虑塑性发展的系数(B)考虑重要性的调整系数(C)考虑单角钢单面连接偏心受力的系数(D)考虑安全的附加系数6.图示T型截面拉弯构件弯曲正应力强度计算的最不利点为。

(A)截面上边缘1点(B)截面下边缘2点(C)截面中和轴处3点(D)可能是1点也可能是2点7.结构或节点的疲劳强度与关系不大。

(A)钢材的种类(B)应力循环次数(C)节点的制作工艺和质量(D)应力集中系数8.为提高梁在弯矩作用下的强度和刚度，应尽可能使梁的。

(A)翼缘厚而窄(B)翼缘宽薄而腹板窄厚(C)腹板厚而窄(D)腹板薄而宽9.对于钢结构用钢材，对化学成分的定义为。

(A)C为不可缺少元素，Mn、S、P均为有害元素(B)C为不可缺少元素，Mn为脱氧剂，S、P为有害元素(C)C、Mn、S、P均为有害元素(D)C、Mn为有害元素，S、P为不可缺少元素10.规范规定缀条式格构柱单肢的长细比（为柱两个主轴方向长细比的最大值），是为了。

(A)保证柱平面内的整体稳定(B) 保证柱平面外的整体稳定(C)避免单肢先于整个柱失稳(D)构造要求11.由于建筑用钢材多为塑性性能好的钢材，故残余应力的存在将。

(A)降低静力承载能力(B)对静力承载能力无影响(C)提高静力承载能力(D)钢材易发生塑性破坏12.开口槽形截面轴心受压构件，当绕对称轴失稳时，构件将发生的失稳变形。

可靠度的响应面法研究彭攀，张淑华河海大学交通、海洋学院，江苏南京（210098）E-mail ：pp630@摘 要：体系可靠度已经成为可靠度研究的重点 ，由于其功能函数大都为隐式功能函数 ，响应面法已成为计算可靠指标的主要方法 ，响应面法主要分为多项式响应面法、神经网络响应面、模糊神经网络响应面 。

本文介绍了近似函数的选择、响应面的建立、试验设计方法、响应面的评价及发展近况。

关键词：可靠度，响应面法，试验设计方法，评价中图分类号：TU3111. 引 言目前 ， 结构的极限状态方程一般都基于抗力——荷载效应模型。

现有可靠度计算方法都是以极限状态方程具有明确的解析表达式为基础的。

但是对于一些复杂的结构系统 ，由于结构本身的复杂性,其基本随机变量的输入与输出量之间的关系数可能是高度非线性的,有时甚至不存在明确的解析表达式,给可靠度的计算带来很大困难。

响应面法正是由于它在处理隐式极限状态问题时的高效性，而被引入到结构可靠性分析中。

响应面法(response surface method ，RSM)最早是由Box 和Wilson 于1951年提出来，用于利用统计学的综合试验技术，处理复杂系统的输入(基本变量)和输出(系统响应)之间的转换关系，用响应面函数(RSF)来拟合原有的隐式极限状态函数。

1984年Wong 首先提出结构可靠度计算的响应面法，并于1985年将其应用于土坡稳定的可靠度计算[1]。

Bucher 等于1990年将响应面法引入结构可靠性分析中，建立结构输入与结构响应之间的关系，然后进行结构可靠性分析[2]。

由于响应面法的精度是由响应面的形式及取样点的点位确定的，所以这两方面便成为响应面法的研究主题。

2. 近似函数的选择2.1 多项式响应面法响应面法是数学方法和统计方法结合的产物，用于处理复杂系统的输入与输出的转换关系问题。

该方法采用有限的试验，通过回归拟合解析表达式z = g (X)代替真实曲面 z = g(X)，可将功能函数近似地表示为随机变量的显式。

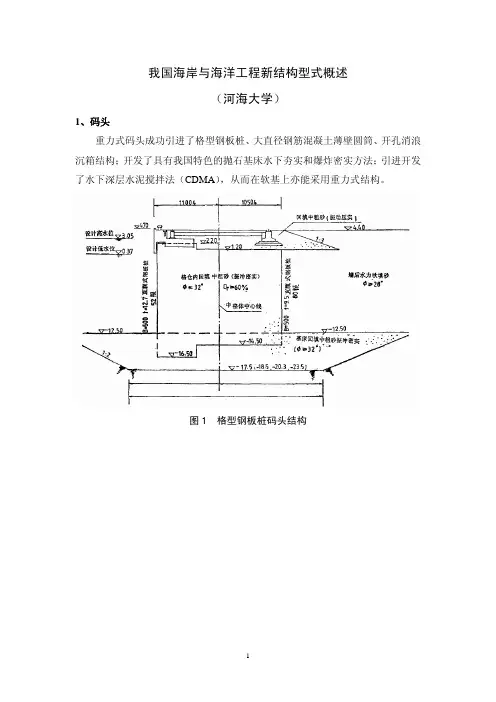
我国海岸与海洋工程新结构型式概述（河海大学）1、码头重力式码头成功引进了格型钢板桩、大直径钢筋混凝土薄壁圆筒、开孔消浪沉箱结构；开发了具有我国特色的抛石基床水下夯实和爆炸密实方法；引进开发了水下深层水泥搅拌法（CDMA），从而在软基上亦能采用重力式结构。

图1 格型钢板桩码头结构图2 大直径钢筋混凝土圆筒码头结构高桩码头在深水情况下成功采用了全直桩结构和依靠自身变形吸收船舶能量的柔性靠船结构。

图3 全直桩码头结构随着板桩码头结构向大型化发展，其结构亦有很大改进，除普通的拉杆式锚碇板桩外，还出现了斜拉（顶）桩式板桩码头和遮帘式板桩码头。

图4 遮帘式板桩码头中交第三航务工程勘察设计院提出了嵌岩导管架码头结构的新型结构型式。

图5 嵌岩导管架码头结构2、防波堤研究开发了爆破填石的防波堤软基处理技术和大空心率空心方块轻型斜波堤；研究开发了削角直立堤、开孔消浪沉箱结构、环保型的梳式沉箱结构及大直径圆筒结构等；研究开发了削角空心方块混合堤和桩基透空堤；引进、吸收、创新推广了半圆型结构混合堤。

3、耐久性高效能减水剂、膨胀剂的研究与应用是水运工程混凝土技术的重大进展；降低水灰比的同时掺入引气剂是提高混凝土抗冻性能的有效措施；钢筋表面封闭材料的应用及钢筋混凝土电化学脱盐防腐技术的开发可有效提高混凝土耐久性；引进开发的纤维混凝土可大大提高其抗裂性和抗冲击性。

我国沿海深水港口建设面临的重大技术问题1、重大基础技术条件（1）模拟技术数学模拟方面重点研究与开发高、新、精、细数学模型；多因素过程数学模型；数学模型和物理模型相结合的复合模型，包括耦合运转型、综合模拟型和混合计算型；智能化可视化数学模型；随机数学模型。

物理模拟方面重点研究与开发开边界的模拟技术、多向波的模拟技术、波流风同时作用的模拟技术；同时模拟悬移质、推移质、冲泻质和床沙质泥沙的技术。

（2）深水设计波浪标准问题现行港口工程技术规范中，对于承受波浪荷载的港口和海岸工程建筑物，主要是针对近岸浅海情况的，对离岸深水情况是否合适，有待深入研究。

钢结构_河海大学中国大学mooc课后章节答案期末考试题库2023年1.同类钢种的钢板，厚度越大，。

答案:强度越低2.最易产生脆性破坏的应力状态是。

答案:三向拉应力状态3.结构或节点的疲劳强度与关系不大。

答案:钢材的种类4.为提高梁在弯矩作用下的强度和刚度，应尽可能使梁的。

答案:腹板薄而宽5.由于建筑用钢材多为塑性性能好的钢材，故残余应力的存在将。

答案:对静力承载能力无影响6.一个普通剪力螺栓在抗剪连接中的承载力是。

答案:螺杆的抗剪承载力和被连接构件(板)的承压承载力两者中的较小值7.摩擦型高强度螺栓连接受剪破坏时，作用剪力超过了。

答案:连接板件间的摩擦力8.钢材脆性破坏同构件无关。

答案:弹性模量9.轴心压杆整体稳定公式的意义为。

答案:构件轴心压力设计值不超过构件稳定极限承载力设计值10.双肢格构式轴心受压柱，实轴为x-x轴，虚轴为y-y轴，应根据确定肢件间距离。

答案:0y＝x11.根据构件截面形式的不同，轴心受压构件的整体屈曲形式可分为弯曲失稳和扭转失稳两种。

答案:错误12.实际轴心受压构件临界力低于理想轴心受压构件临界力的主要原因有初弯曲、初偏心和残余应力的影响。

答案:正确13.钢结构计算的两种极限状态是承载能力极限状态和正常使用极限状态。

答案:正确14.钢材的破坏形式有脆性破坏和塑性破坏。

答案:正确15.钢材的三项主要力学性能为抗拉强度、屈服强度和延伸率。

答案:正确16.确定梁截面高度时，由建筑层高确定最小高度，由刚度条件确定最大高度。

答案:正确17.焊接的连接形式按构造可分为角焊缝和对接焊缝两种类型。

答案:正确18.凡能通过一、二级检验标准的对接焊缝，其抗拉设计强度与母材的抗拉设计强度相等。

答案:正确。

一、如图所示混凝土重力坝段。

已知坝顶宽度B＝9.0m；坝高H=131.0m；上游坡比m1=0.15；下游坡比m2=0.72;坝底到上游折坡点的高度H0=124m。

已知随机变量和统计量为：1.混凝土容重γc＝（24.0kN/m3，0.018，正态分布）；2.上游水位Hs＝（119m，0.06，正态分布）；3.下游水位Hx＝（25m，0.055，正态分布）；4.扬压力系数α＝（0.35，0.15，极值Ⅰ型分布）；5.摩擦系数f＝（0.72，0.25，对数正态分布）；6.凝聚力c＝（600kN/m2，0.6，极值Ⅰ型分布）；7.混凝土抗压强度Rc＝（9980kN/m2，0.23，对数正态分布）。

用JC法计算该混凝土重力坝段的可靠度。

作业要求：要求给出计算程序、计算步骤。

1.给出求解可靠指标的程序框图；2.编制计算程序并计算出满足精度要求的结果；3.试用截尾JC法计算该混凝土重力坝段的可靠度并进行分析比较。

一．混凝土重力坝可靠度计算1. 程序流程2. 可靠度方程的建立混凝土重力坝失稳形式有:坝段抗滑失稳和坝段抗剪短失稳混凝土重力坝坝段的可靠度有：（1）坝段抗滑稳定的可靠度；（2）坝段抗压强度稳定的可靠度。

现计算混凝土重力坝坝段的可靠度如下，取单位宽度的坝段进行计算。

（1）坝段抗滑稳定的可靠度1. 建立坝段抗滑稳定极限状态方程坝段抗滑稳定的极限状态方程为。

运用抗剪断强度公式计算抗滑稳定的极限状态方程为：1°竖向力（不包含）坝体自重：上游水重：下游水重：竖向力：2°扬压力3°上游水压力4°下游水压力说明：a.计算上游水重时，近似认为上游水位低于上游折坡处，故水重按三角形计算；b.扬压力折减处距坝踵L。

L根据SL319-2005《混凝土重力坝设计规范》中对廊道的规定，再结合排水孔，近似取L=10m。

综上，抗滑稳定的极限状态方程为：2.对于非正态分布的的变量先进行当量正态化：在设计验算点x*对数正态分布变量f与Rc的μ与σ：标准差：均值：其中：在设计验算点x*极值Ⅰ型分布变量α与c的参数α与k：则其概率密度和分布函数分别为由当量正态化条件得3. 列出Matlab程序语言编制的JC法程序所需相关公式4.编写Matlab程序语言编制的JC法程序,程序代码:clear;clc;muX=[24;119;25;0.35;0.72;600]; %均值sigmaX=[0.018;0.06;0.055;0.15;0.25;0.6]; %方差%将对数正态分布转化为正态分布，求当量正态化后的方差和均值sLn=sqrt(log(1+(sigmaX(5)/muX(5))^2));mLn=muX(5)-sLn^2/2;% 将极值Ⅰ型分布当量正态化，求当量正态化后的方差和均值aEv4=sqrt(6)*sigmaX(4)/pi;uEv4=-psi(1)*aEv4-muX(4);aEv6=sqrt(6)*sigmaX(6)/pi;uEv6=-psi(1)*aEv6-muX(6);muX1=muX;sigmaX1=sigmaX;x=muX; normX=eps;while abs(norm(x)-normX)/normX>1e-6normX=norm(x); g=(6807.81*x(1)+0.735*x(2)^2+3.528*x(3)^2-49*x(2)-528.612*x(4)*x(2)-1008.224*x(3)+528.612*x(4)*x(3))*x(5)+107.88*x(6)-4.9*x(2)^2+4.9*x(3)^2;gX=[6807.81*x(5);(1.47*x(2)-49-528.612*x(4))*x(5)-9.8*x(2);(7.056*x(3)-1008.224+528.612*x(4))*x(5)+9.8*x(3);(-528.612*x(2)+528.612*x(3))*x(5);6807.81*x(1)+0.735*x(2)^2+3.528*x(3)^2-49*x(2)-1008.224*x(3)-528.612*x(2)*x(4)+528.612*x(3)*x(4);107.88];%logncdf求对数分布累积分布函数，evcdf求极值分布累积分布函数cdfX=[1-evcdf(-x(4),uEv4,aEv4);logncdf(x(5),mLn,sLn);1-evcdf(-x(6),uEv6,aEv6)];%gnpdf求对数分布概率密度函数，evpdf求极值分布概率密度函数pdfX=[evpdf(-x(4),uEv4,aEv4);lognpdf(x(5),mLn,sLn);evpdf(-x(6),uEv6,aEv6)];cdfX(cdfX<eps)=0.001;cdfX(cdfX>0.999)=0.999;pdfX1=pdfX;pdfX(pdfX<eps)=1;%norminv求逆nc=norminv(cdfX);sigmaX1(4:6)=normpdf(nc)./pdfXmuX1(4:6)=[x(4:6)-nc.*sigmaX1(4:6)];gs=gX.*sigmaX1;alphaX=-gs/norm(gs);bbeta=(g+gX'*(muX1-x))/norm(gs)x=muX1+bbeta*sigmaX1.*alphaXend5.编写Matlab程序编制的JC法，得出结果，由不考虑截尾分布的JC法程序计算得坝段的抗滑稳定可靠指标，其对应的失效概率为：求得最终结果：可靠度：b =3.0902验算点坐标：x =[24.0000, 119.0000, 25.0000, 2.5905, 0.0736, 599.9014]（2）坝段抗压强度稳定的可靠度1. 建立坝段抗压强度稳定极限状态方程坝段抗压强度稳定极限状态方程。

工程结构可靠度分析学院：姓名：学号：指导教师：目录一、工程概况 (1)二、计算依据和参考 (3)三、分析模型和参数 (4)3.1 计算模型 (4)3.2 计算模型参数 (5)四、可靠指标计算 (12)4.1 Monte Carlo方法简介 (12)4.2 响应面方法简介 (12)4.3 可靠指标的计算 (13)附录：ANSYS APDL命令流 (25)一、工程概况冷水江市资江二桥为一独塔双索面、完全对称、塔梁墩固结的斜拉桥，设置有22对、上下游2个索面斜拉索，共计88根。

试考虑部分参数的随机性，应用ANSYS PDS 模块计算在各施工工况（最多悬臂施工至第10对索已经张拉），由于突发断索导致的主梁、索塔、桥墩、斜拉索抗弯、抗拉、抗裂性等指标失效概率的变化（响应面法 + Monte Carlo ）。

主梁标准断面如图1-1所示，索塔断面如图1-2所示。

A-A342252,5图1-1 主梁标准断面（单位：m ）Ⅲ-ⅢⅣ-Ⅳ909010010022090909047090140140909040022090909047090400R 90R 90图1-2-a 索塔空心断面（单位：cm ）Ⅴ-ⅤⅥ-Ⅵ2209090904709040032090909057090500R 9R 9图1-2-b 索塔实心断面（单位：cm ）题目编号2：工况：断索位置，仅一侧（9#拉索）；计算内容（可靠指标）：拉索抗拉能力（8#、10#），索塔抗弯、抗裂性。

二、计算依据和参考1、《公路工程技术标准》JTG B01-20032、《公路桥涵设计通用规范》JTG D60-20043、《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTG D62-20044、《公路工程结构可靠度设计统一标准》GB/T 50283-1999三、分析模型和参数3.1 计算模型主梁、索塔、桥墩建模时可考虑尽量采用标准节段，主梁横隔板按节点荷载计入。

拉索锚固点塔端以钢锚梁上锚固坐标为准，锚点与建模节点间通过刚臂连接。

第一章概论一、钢结构的特点可靠性高/材料的强度高，钢结构自重轻/钢材的塑性和韧性好/钢结构制造简便，施工工期短/钢结构密闭性好/钢材的耐锈蚀性差/钢结构耐热但不耐火/钢材在低温时脆性增大二、结构设计的目的任何结构都是为了完成所要求的某些功能而设计的。

工程结构必须具备下列功能：1. 安全性结构在正常施工和正常使用条件下，承受可能出现的各种作用的能力，以及在偶然事件发生时和发生后，仍保持必要的整体稳定性的能力。

2. 适用性结构在正常使用条件下，满足预定使用要求的能力。

3. 耐久性结构在正常维护条件下，随时间变化而仍能满足预定功能要求的能力。

结构的安全性、适用性、耐久性总称为结构的可靠性。

结构设计（计算）的目的是在满足各种预定功能的前提下，做到技术先进、安全适用、经济合理和确保质量。

要实现这一目的，必须借助于合理的设计方法。

结构设计应考虑下列两种极限状态：（1）承载能力极限状态结构或构件达到最大承载能力，或达到不适于继续承载的变形的极限状态。

如限制受弯构件截面上塑性区的发展不能超过某一限值，就是考虑使其不致产生不适于继续承载的变形的一个例子。

（2）正常使用极限状态结构或构件达到使用功能上允许的某一限值的极限状态。

第二章钢结构的材料一、钢材的破坏形式1. 塑性破坏：钢材在产生很大的变形以后发生的断裂破坏称为塑性破坏，也称为延性破坏。

变形大，变形持续时间长，易及时发现和补救。

2. 钢材在变形很小的情况下突然发生断裂破坏称为脆性破坏。

变形很小且突然发生，不易发现和采取补救措施，因而危险性很大。

二、钢结构对所用材料的要求物美价廉1. f u、f y高。

用到f y，f y高可减轻结构自重。

f y/f u太小浪费，太大安全储备小。

通常在0.6～0.7。

2. 塑性、韧性、耐久性好。

可防止脆性破坏，抗动力荷载好，耐疲劳。

3. 良好的加工性能。

冷、热加工和可焊性好。

4. 耐腐性好。

5. 价格便宜。

6. 有时还要求钢材具有适应低温、高温等环境的能力。

1承受动力荷载作用的钢结构，应选用塑性，冲击韧性好的钢材。

2冷作硬化会改变钢材的性能，将使钢材的屈服点提高，塑性和韧性降低。

3钢材五项机械性能指标是屈服强度、抗拉强度、冷弯性、伸长率、冲击韧性。

4钢材中氧的含量过多，将使钢材出现热脆现象。

5钢材含硫量过多，高温下会发生热脆，含磷量过多，低温下会发生冷脆。

6时效硬化(老化)会改变钢材的性能，将使钢材的强度提高，塑性韧性降低。

7影响钢材性能的因素：化学成分，成材过程，钢材硬化，温度，集中应力，反复荷载作用8钢材在250ºC度附近有抗拉强度、硬度提高伸长率降低现象，称之为蓝脆现象。

9钢材硬化的三种情况;冷作硬化，时效硬化，应变时效硬化10钢材的主要性能：抗拉强度，屈服强度，伸长率12钢材牌号Q235－BF,其中235表示屈服强度 ,B表示质量等级B级 ,F表示沸腾钢。

13钢材的三脆是指热脆、冷脆、蓝脆。

14焊接结构选用焊条的原则是,计算焊缝金属强度宜与母材强度相适应。

15钢材中含有C、P、N、S、O、Cu、Si、Mn、V等元素,其中S P O N为有害的杂质元素。

16衡量钢材塑性性能的主要指标是伸长率。

17结构的可靠指标β越大,其失效概率越小。

18承重结构的钢材应具有屈服强度、抗拉强度、伸长率和冷弯性、硫磷极限含量的合格保证,对焊接结构尚应具有含碳量的合格保证;对于重级工作制和起重量对于或大于50 t中级工作制焊接吊车梁类似结构的钢材,应具有常温冲击韧性的保证。

19冷弯性能合格是鉴定钢材在弯曲状态下塑性变形能力和钢材质量的综合指标20结构有哪两种极限状态：承载能力极限状态，正常使用极限状态21工程结构必须具备哪些功能：安全性，使用性，耐久性，总称为结构的可靠性22疲劳破坏的三个阶段：裂纹的形成，裂纹的缓慢扩展，迅速断裂23钢材的选择：结构的重要性，荷载的性质，连接方法，工作环境，钢材厚度24焊缝连接形式：对接搭接T形连接角部连接25钢结构的连接方法通常有焊缝连接，铆钉连接和螺栓连接三种。

《结构可靠度理论与应用》1、如图所示圆截面直杆，承受拉力P=120KN ，已知材料的强度设计值f y 的均值μfy =310MPa ，标准差为σfy =25MPa ，杆直径d 的均值μd =30mm ，标准差为σd =3mm ，在功能函数为：（1）2(/4)Z d r F π=- ；（2）24/Z r F d π=- ，在这两种情况下，试用中心点法求其可靠度指标和可靠度。

程序：clear;clc;muX=[310;30];sigmaX=[25;3]; Z=pi/4*muX(2)^2*muX(1)-120e3; Zx=[pi/4*muX(2)^2;pi/2*muX(1)*muX(2)]; betaC1=Z/norm(Zx.*sigmaX) Pr1=normcdf(betaC1)Z=muX(1)-4/pi*120e3/muX(2)^2; Zx=[1;8*120e3/pi/muX(2)^3]; betaC2=Z/norm(Zx.*sigmaX) Pr2=normcdf(betaC2) 运行结果：betaC1 =2.0977 Pr1 =0.9820 betaC2 =3.3259 Pr2 = 0.99962、粒状土承受剪切应力τ=52KPa ，其剪切面法向应力w 服从正态分布，均值为100KPa ，标准差为20KPa ，土的磨擦角φ服从正态分布，均值为35º，标准差为5º(=0.0873弧度)。

w 和φ相互独立，极限状态方程为：Z=wtan φ-τ=0，用中心点法计算β值和失效概率pf 。

程序：clear;clc;muX=[100;35*pi/180];sigmaX=[20;5*pi/180]; Z=muX(1)*tan(muX(2))-52;Zx=[tan(muX(2)); muX(1)/cos(muX(2))^2]; betaC=Z/norm(Zx.*sigmaX) Pf=normcdf(-betaC) 运行结果：betaC =0.9429 Pf =0.17293、某钢梁承受确定性弯矩138M kN m =⋅，抗弯截面模量63(89010,0.05)W W W m μδ-=⨯=，服从正态分布；钢材强度f 服从对数正态分布（262,f MPa μ=0.1f δ=），极限状态方程为Z fW M =-=0。

大型非线性结构可靠度计算方法研究
陆军;武清玺
【期刊名称】《水科学与工程技术》
【年(卷),期】2010(000)006
【摘要】拱坝是水利工程中的常见结构,因坝体材料的物理参数和作用于坝体的荷载均是随机变量,故坝体的应力和变形呈现出不确定性.因此,在拱坝设计和研究中,以概率统计理论为基础,对拱坝进行可靠度分析是科学、合理的.由于拱坝体量大,构造复杂,且基岩和筑坝材料具有非线性特性,使拱坝结构的可靠度分析十分困难.将可靠度计算的响应面法与拱坝应力分析的有限元法相结合,应用成熟的有限元分析软件,分析拱坝的可靠度.坝体应力与变形的计算采用三维非线性有限元法,可靠度计算采用二次响应面法.针对福建省永泰县大洋水电站拱坝的可靠度分析,得出了可靠指标的变化规律.与其他可靠度分析方法相比,该方法可以直接应用确定性的结构计算程序,使大型非线性结构的可靠度分析工作更加简便可行.
【总页数】4页(P57-60)
【作者】陆军;武清玺
【作者单位】河海大学,土木工程学院,南京,210098;河海大学,土木工程学院,南京,210098
【正文语种】中文
【中图分类】TV314
【相关文献】
1.大型非线性结构可靠度计算方法研究 [J], 陆军
2.超大型FPSO结构总纵强度随机可靠度计算 [J], 杨利敏
3.钢筋混凝土梁—板结构可靠度计算方法研究 [J], 张程;孙晋莉
4.钢筋混凝土梁—板结构可靠度计算方法研究 [J], 张程;孙晋莉;
5.非线性结构可靠度设计的计算应用分析 [J], 胡成荣;赵文才
因版权原因，仅展示原文概要，查看原文内容请购买。