西工大可靠性设计大作业

机械可靠性设计大作业题目：扭杆姓名：刘昀班号：05021104学号：2011301259日期：2014.12.5机械可靠性设计大作业一、题目：扭杆：圆截面直径D为（μ，σ）=（20，0.1）mm，受扭矩T为（μ，σ）=（677400，8891.28）N.mm，工作循环次数N≥4000，材料疲劳极限S为（μ，σ）=（686.9，35.8）MPa。

二、思路：给定强度分布与应力有关的随机参数分布条件，确定应力计算公式，计算相应的分布参数，假定各随机变量都服从正态分布。

然后根据应力--强度干涉理论计算可靠度，主要考虑载荷的均值与方差两项变化可靠度如何变化，以上要求编程实现。

三、输入的数据：扭矩T的均值与标准差T（μ），T（σ）四、输出的结果：可靠度R五、计算的模型：（1）几何参数（扭杆圆截面直径）D、扭矩T和工作循环次数大于等于4000时的材料疲劳极限，亦即此时的疲劳强度S，均为随机变量且服从正态分布；（2）应力--强度干涉模型：大多数机电产品的应力和强度都是服从一定统计分布规律的随机变量，我们用L表示应力，S表示强度。

它们的概率密度函数f(S)和f(L)两曲线出现部分交叉和重叠，亦即出现干涉时，有可能出现强度小于应力的情况，但可把这种引起失效的概率限制在允许的范围内。

在干涉的情况下，我们研究的是如何在保证一定可靠度的前提下，使零件结构简单、重量较轻，价格较低。

对于强度和应力均为正态分布时，我们采用联结方程来计算可靠度，公式如下：SM称为可靠性系数，在已知、、、的条件下，利用上式可直接计算出SM，根据SM从标准正态分布表中查出可靠度R的值。

也即：六、程序流程图Y七、算例分析结果说明及结论（1）程序运行结果T(μ)↑，T(σ)不变时，可靠度R的变化情况：T(μ) T(σ) R677.4 8.89128 0.99960677.4 8.89128 0.999 120677 8.89128 0.999180677 8.89128 0.999240677 8.89128 0.999300677 8.89128 0.999360677 8.89128 0.999420677 8.89128 0.999480677 8.89128 0.999540677 8.89128 0.999600677 8.89128 0.999660677 8.89128 0.999720677 8.89128 0.999780677 8.89128 0.998999 840677 8.89128 0.998982 900677 8.89128 0.997976 960677 8.89128 0.9782411.02068e+006 8.89128 0.840541 1.08068e+006 8.89128 0.487613 1.14068e+006 8.89128 0.14605 T(μ)↑，T(σ)↑时，可靠度R的变化情况：T(μ) T(σ) R677.4 8.89128 0.99960677.4 508.891 0.999 120677 1008.89 0.999180677 1508.89 0.999240677 2008.89 0.999300677 2508.89 0.999360677 3008.89 0.999420677 3508.89 0.999480677 4008.89 0.999540677 4508.89 0.999600677 5008.89 0.999660677 5508.89 0.999720677 6008.89 0.999780677 6508.89 0.998999840677 7008.89 0.998979900677 7508.89 0.997884960677 8008.89 0.9772671.02068e+006 8508.89 0.8379891.08068e+006 9008.89 0.4877451.14068e+006 9508.89 0.149169（2）结果分析及说明T(μ)↑，T(σ)不变时，可靠度R随着扭矩均值T(μ)的增大而减小，并且当扭矩T(μ)达到一个值840677KN.mm附近时，可靠度开始急剧下降，所以在该扭矩作用下，零件刚好达到了它的材料疲劳极限，因此失效可能性急剧增大。

零部件的可靠性设计班级：学号：姓名：文威威摘要:本学期选修了电子设备可靠性工程，对这项科学有了更深的了解，进一步了解了本学科在工业生产和科学研究上的重要性。

据国外有关资料介绍，在船用电子设备的故障原因中，属设计不合理的占40%,电子元器件质量问题约占30%,曲操作和维护引起的故障占1 0 %,由制造工艺引起的故障约占1 0 %;对我国某炮瞄雷达现场故障统计数据分析表明，约有25%以上是山设计不合理所造成的。

引言:在可靠性技术迅速发展的今天，从指标试验评价发展到从指标论证、设计、原材料选择到工艺控制及售后服务的全过程的综合管理和评价，许多产品打出“零失效”的王牌。

产品的可黑性在很大程度上取决于设计的正确性, 而这乂基于零部件的可靠性设计。

零部件的可鼎性设计是以提高产品可靠性为LI的、以概率论与数理统汁理论为基础，综合运用数学、物理、丄程力学、机械工程学、人机工程学、系统工程学、运筹学等多方面的知识来研究机械工程的最佳设计问题。

利用可黑性设讣,可以降低元器件及系统的使用失效率，降低设备的成本，提高设备的可鼎性。

电子设备可靠性设计技术主要包括热设计、降额设汁、动态设计、三防设计、电磁兼容设计、振动与冲击隔离设计等。

正文：国内外的实践经验表明，机械结构的可靠性是由设计决定的，而由制造、安装和管理来保证的。

因此将概率设计理论和可黑性分析与设计方法应用于机械结构设讣中，才能得到既有足够安全可靠性，乂有适当经济性的优化结构。

这样，以估计结构系统可鼎度为LI标的、以概率统讣和随机过程理论为基础的、以各种结构分析技术为工具的多种结构可鼎性分析与设计方法迅速发展oRaize r综述了一次二阶矩法和以一次二阶矩法为基础的现代可靠性分析理论。

赵国藩等建立了广义随机空间内考虑随机变量相关性的结构可靠度实用分析方法，扩大了现有可幕度计算方法的适用范围。

并且贡金鑫和赵国藩还研究了原始空间内的可靠性分析方法，这种方法不需要将非正态随机变量映射或当量正态化为正态随机变量，因而特别适合于当随机变量的概率分布函数不存在显式时可靠度的讣算。

22 春西北工业大学《质量控制及可靠性》在线作业一答案参考1. 仪器用于日常生产分析时，每班用 ( )对仪器进行运行检查，以监控仪器的工作状态。

参考答案：监控样品2. 试指出下面哪一种说法是正确的?( )A . 质量数最大的峰为份子离子峰B . 强度最大的峰为份子离子峰C . 质量数第二大的峰为份子离子峰D . 降低电离室的轰击能量，强度增加的峰为份子离子峰参考答案： D3. 调查表的种类不包括( )。

A.不良项目调查表B.缺陷位置调查表C.频数调查表D.频率调查表参考答案： D4. 质量管理体系的四大要素包括( )。

A.管理职责﹔资源管理﹔产品的实现﹔测量、分析和改进B.管理承诺﹔资源管理﹔产品的实现﹔测量、分析和改进C.管理职责﹔资源管理﹔管理承诺﹔测量、分析和改进D.管理职责﹔管理策划﹔产品的实现﹔测量、分析和改进参考答案： A5. 极谱分析中，与扩散电流无关的因素是( )A . 电极反应电子数B . 离子在溶液中的扩散系数C . 离子在溶液中的迁移数D . 电极面积参考答案： C6. 下列( )项不属于并行工程的基本原则。

下列( )项不属于并行工程的基本原则。

A.突出人的作用B.关注早期设计阶段C.重视顾客需求D.独立工作参考答案： D7. 膨胀机带液如何处理?膨胀机带液如何处理?本题答案： 1)即将关闭紧急切断阀，住手膨胀机。

2)关闭膨胀机的进口阀。

3)打开膨胀机的紧急切断阀、喷嘴、蜗壳吹除阀，将膨胀机内及机后管道的液体排放干净。

4)如果下塔液位过高，排放下塔液面到规定值。

5)打开机前的吹除阀将机前的管道的液体排放干净。

6)以上工作结束后，按启动膨胀机的要求准备关闭或者打开各阀门。

8. 库仑分析与普通滴定分析相比( )。

A . 测量精度相近B . 需要标准物进行滴定剂的校准C . 不需要制备标准溶液，不稳定试剂可以边产生边滴定D . 很难使用不稳定的滴定剂参考答案： C9. 以下对质量管理体系基本内涵的描述不正确的是( )。

诚信保证本人知晓我校考场规则和违纪处分条例的有关规定，保证遵守考场规则，诚实做人。

本人签字： 编号：西北工业大学考试试题（卷）2006－2007学年第二学期开课学院 五 课程 机械可靠性设计 学时 32考试日期 2011.12.25 考试时间 2 小时 考试形式（闭开）（BA）卷题号 一二三四五六七总分得分考生班级05030801学 号姓 名一、概念题（每题3分，共计30分）（前5个为填空，后5个为判断正误）1、有500件产品，工作至800小时有50件失效，此时t=800小时时该产品的可靠度为①。

2、由三人监视作业时，有两人以上同意才能切断电源，n=3,则其操作可靠度为①，设每个人正确操作的概率为R。

3、已知某材料抗拉强度为580~780Mpa，该材料的抗拉强度的均值和标准差分别为①和②。

4、有一汽车的制动系统，可靠度为Rs=0.98，该系统由两个块式制动器并联构成，要求每个制动器的可靠度应为①。

注：1. 命题纸上一般不留答题位置，试题请用小四、宋体打印且不出框。

2. 命题教师和审题教师姓名应在试卷存档时填写。

共6页 第1页成绩5、 有四个单元，可靠度均为0.9，要求所组成系统的可靠度大于0.9的方案有几种①。

6、浴盆曲线是失效概率在工作时间内的描述，反映了产品在整个使用过程中失效状况。

（ × ）7、在减速器的齿轮设计中，齿轮上所受的载荷、齿轮齿宽等几何参数为随机变量。

（ × ）8、产品致命度与产品失效概率成反比。

（ × ）9、在人机系统中，人操作的可靠度比机器的可靠度重要的多。

（ √ ）10、人—机—环境所组成系统的可靠度为三者可靠度之积计算。

（ √ ）二、解释名词（每题3分，共计15分）1、MTTF与MTBF：2、FMECA与FTA：3、维修度：4、应力——强度干涉模型：5、冗余技术：教务处印制 共6页 第2页三、问答题(每小题5分,共20分)1、什么是表决系统？它的可靠度与串、并联系统相比有什么特点？2、可靠性分配、可靠性预测与可靠性分析三者在可靠性系统设计各强调的内容是什么？之间有何联系？3、什么是最小割集和最小路集？在失效树分析中有何作用？4、无替换定数截尾与有替换定数截尾寿命试验有何不同？四、计算题(共35分)1、设有N=100个产品，从t=0开始运行，在50h内无失效，在50h至51h内发生一个失效，在51h至52h内发生3个失效，求该批产品在50h及51h的失效率。

西北工业大学智慧树知到“工业工程”《质量控制及可靠性》网课测试题答案（图片大小可自由调整）第1卷一.综合考核(共10题)1.偶然性原因是可以避免的。

()A.错误B.正确2.()是一种在产品设计和开发过程中用于表明顾客要求的质量特性与产品功能间关系的简明图表，是描述质量展开过程和结果的有效工具。

A.QC工序表B.因果图C.质量表D.方差分析表3.调查表的种类不包括()。

A.不良项目调查表B.缺陷位置调查表C.频数调查表D.频率调查表4.质量管理体系的四大要素包括()。

A.管理职责﹔资源管理﹔产品的实现﹔测量、分析和改进B.管理承诺﹔资源管理﹔产品的实现﹔测量、分析和改进C.管理职责﹔资源管理﹔管理承诺﹔测量、分析和改进D.管理职责﹔管理策划﹔产品的实现﹔测量、分析和改进5.以下属于质量检验阶段的特点的是()。

A.质量检验属于事中把关B.不能够减少因废品而造成的损失C.对避免因不合格品出厂而给用户造成的损失起到了很好的质量把关作用D.能预防废品产生6.5W1H中的“H”代表了顾客需求。

()A.错误B.正确7.下列关于质量检验的定义正确的是()。

A.对产品或服务的一种或多种特性进行测量、检查、试验、计量，并将这些特性与规定的要求进行比较，以确定其符合性的活动B.通过技术专家对产品使用性能进行评价C.通过观察和判断，结合测量、试验所进行的符合性评价D.根据产品标准对原材料、中间产品、成品合格与否给出结论8.下列关于质量功能展开(QFD)的说法，不正确的是()。

A.QFD于20世纪60年代末70年代初起源于日本B.QFD于80年代初传入欧美C.QFD坚持“以顾客为关注焦点”的原则D.QFD不利于缩短开发周期9.产品的设计、制造及企业经营管理等各项活动都离不开人的参与，而且必须以人为主导，这体现了全面质量管理()基本思想。

A.以顾客为中心B.预防为主，防患于未然C.突出人的作用D.过程方法、体系保障10.质量文化整体上分为三个层次，()是质量文化的核心层，通过员工的质量意识、质量观念、质量精神所表现。

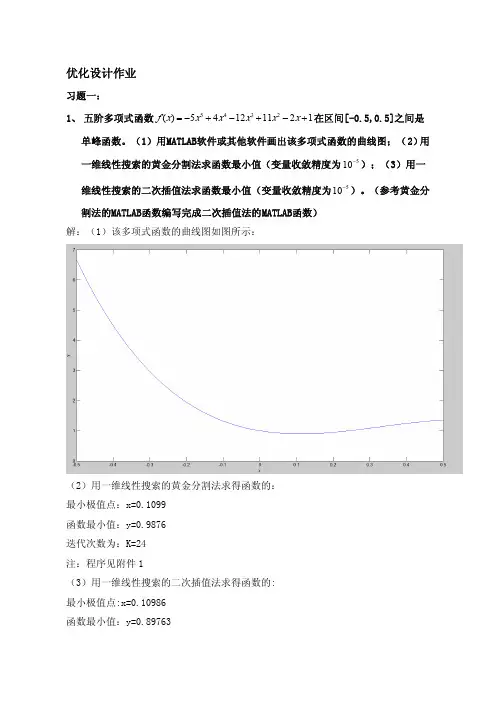
优化设计作业习题一：1、五阶多项式函数5432()54121121f x x x x x x =−+−+−+在区间[-0.5,0.5]之间是单峰函数。

（1）用MATLAB软件或其他软件画出该多项式函数的曲线图；（2）用一维线性搜索的黄金分割法求函数最小值（变量收敛精度为510−）；（3）用一维线性搜索的二次插值法求函数最小值（变量收敛精度为510−）。

（参考黄金分割法的MATLAB函数编写完成二次插值法的MATLAB函数）解：（1）该多项式函数的曲线图如图所示：（2）用一维线性搜索的黄金分割法求得函数的：最小极值点：x=0.1099函数最小值：y=0.9876迭代次数为：K=24注：程序见附件1（3）用一维线性搜索的二次插值法求得函数的:最小极值点:x=0.10986函数最小值：y=0.89763注：程序见附件22、方程220.2()ln (2)ln (10)f x x x x =−+−−,在区间[6,9.9]之间是单峰函数。

重复第一题的3个小问题。

解：（1）该多项式函数的曲线图如图所示：（2）用一维线性搜索的黄金分割法求得函数的：最小极值点：x=8.5016函数最小值：y=2.1338迭代次数为：K=27注：程序见附件1（3）用一维线性搜索的二次插值法求得函数的:最小极值点：x=8.501589函数最小值：y=2.133838注：程序见附件23、用牛顿法求解（牛顿法的MATLAB程序给出）（变量收敛精度为510−）：(1)min 22112212()2 1.52f x x x x x x x =−++−0[1,1]Tx =(2)将函数4231122()32f x x x x x =−+在点0[1,1]T x =简化为二次函数，并用牛顿法求此二次函数的最优解。

解：（1）最小值点为0.4999999586298150.999999966693309x ⎡⎤=⎢⎥⎣⎦极小值为-0.7499999999999(9)9f x =迭代次数2k =（2）最小值点为 1.0606601535905480.749999985401338x ⎡⎤=⎢⎥⎣⎦极小值为-0.4218749999999(9)9f x =注：程序见附件34、用最速下降法（或其它相应的无约束优化方法）求上述第三大题（程序参照牛顿法的程序自己编写）。

西工大可靠性复习资料总结T系统的工作时间，tiT时间内单元的工作时间，Ni第i个单元的重要零件数，N系统的重要零件总数，Ei第i个单元的重要度。

Ei=由第i个单元的失效而造成系统失效的次数/第i单元的失效次数。

分给i的可靠度39可靠性分析：利用归纳、演绎的方法对系统可能发生的故障进行研究，研究失效的原因、后果和影响及严重程度，从而为系统设计提供改进建议。

分析方法：1FMECA法2失效树分析（FTA）40FEMCA：在系统设计过程中，通过对系统各组成单元潜在的各种失效模式及其对系统功能影响，与产品和后果的严重成都进行分析，提出采取的预防改进措施，以提高产品的可靠性的一种设计分析方法。

包含FMA（失效模式分析）、FEA （失效影响分析）、FCA（失效致命度分析）如何进行：按照FMECA表哥逐项分析和填表。

41FMECA基本任务：1查明一切失效模式及其对系统功能造成的影响和后果，判断其严重性等级。

2查明单点失效项目并逐渐评价其发生概率大小。

3完成FMECA报告，内容包括：系统可靠性关键零件清单，改进或补偿措施。

对哪些致命度大零部件进行更换，增加冗余或修改设计，力争将潜在的致命度打的失效消灭在设计阶段。

42失效后果等级：分析失效模式出现对系统工作功能或状态引起的各种后果。

把各种失效模式的后果进行定性分类，分为四类I灾难性的，可能造成人身死亡或全系统损坏。

II关键性的导致系统不可能完成规定的功能，III 边缘的可能造成次要损坏或系统性能下降IV次要的，不造成系统损失，但可能要求计划外的维修。

概率等级：用失效模式出现的概率可定型反映零部件失效率，失效模式出现的概率是以某一失效模式出现数除以全系统失效次数来计算的。

分为个等级A经常的概率约20%，B相当可能的10%~20%，C偶然的1%~10%,D小的概率0、1%~1%，E级极不可能的概率小于0、1%。

43致命度：根据失效后果等级和概率等级，致命度分为四级1级IA；2级IB，IIA；3级IC，IIB, IIIA；4级ID, IIC, IID ,IIIB, IIIC, IIID, IVA, IVB, IVC, IVD, IE, IIE, IIIE, IVE。

机械可靠性设计实验报告学院：机电学院班级：05021104姓名：张木学号：2011301279题目：齿轮：某种机器的齿轮，按国标规定的方法计算或查线图得到各参量的均值和标准差如下,求齿轮的可靠度。

分析：分别计算齿轮齿面接触疲劳强度的可靠度与齿轮齿根弯曲疲劳强度的可靠度后进行比较，取可靠性较小值作为齿轮的可靠度。

12(34644,519.66),(1,0.033),(1.484,0.1613),(1.68,0.0544)(1.603,0.052889),(1.16,0.03828),2(200,1),(148.75,0.74375),(4,0.02),(2.32,0.0116)(189.8,9.49)(),t A V H F H F n H E F N K K K K K K b mm d mm m mm Z Z N mm Z ββααε============2lim (0.81,0.00405),(0.957,0.004785)(1300,156),(1,0.033),(1.03,0.03399)(1.04,0.3432),(0.92,0.03036),(1,0.033),(1,0.033)H N R V L W X Z N mm Z Z Z Z Z Z βσ=========程序流程图：开始计算齿轮零件的齿面接触和齿根弯曲疲劳强度均值uT1，uT2和标准差sT1，sT2根据公式计算应力的均值ut1，ut2和标准差st1，st2然后根据应力和强度的连结方程计算可靠性系数SM1，SM2计算出可靠度R1，R2比较R1，R2，取较小值结束程序1：基于齿面接触强度的可靠性#include <iostream>#include <cmath>using namespace std;#define PI 3.141592653double fun(double x,double miu,double sigma){return 1/(sqrt(2*PI)*sigma)*exp(-((x-miu)*(x-miu))/2/sigma/sigma);}double integral(double miu,double sigma,double a,double b){double s,h;int i;int N=abs(a-b)/0.001;s=(fun(a,miu,sigma)+fun(b,miu,sigma))/2.0;h=(b-a)/N;for(i=1;i<N;i++)s+=fun(a+i*h,miu,sigma);return(s*h);}double sigmaadd(double sigma_c,double sigma_d){return sqrt(sigma_c*sigma_c+sigma_d*sigma_d);}double sigmacheng(double a,double sigma_a,double b,double sigma_b){returnsqrt(a*a*sigma_b*sigma_b+b*b*sigma_a*sigma_a+sigma_b*sigma_b*sigma_a*sigma_a); }double sigmachu(double a,double sigma_a,double b,double sigma_b){return 1/b*sqrt((a*a*sigma_b*sigma_b+b*b*sigma_a*sigma_a)/(b*b+sigma_b*sigma_b)); }int main(){double kf,sigma_kf,ka,sigma_ka,kv,sigma_kv,khb,sigma_khb;double khx,sigma_khx,b,sigma_b,d1,sigma_d1,sigma_v;double zh,sigma_zh,ze,sigma_ze,zt,sigma_zt,v;double zb,sigma_zb,sigmahlim,sigma_sigmahlim,zn,sigma_zn;double zr,sigma_zr,zv,sigma_zv,zl,sigma_zl,zw,sigma_zw;double zx,sigma_zx,ft,sigma_ft,kx,sigma_kx,result;double x,sigma_x,y,sigma_y,u,c,sigma_c,t,sigma_t,R,sigma_R;ft=34644;sigma_ft=519.66;ka=1;sigma_ka=0.033;kv=1.484;sigma_kv=0.1613;khb=1.68;sigma_khb=0.0544;kx=1.16;sigma_kx=0.03828;b=100;sigma_b=0.5;d1=148.75;sigma_d1=0.74375;zh=2.32;sigma_zh=0.0116;ze=189.8;sigma_ze=9.49;zt=0.81;sigma_zt=0.00405;zb=0.957;sigma_zb=0.004785;sigmahlim=1300;sigma_sigmahlim=156;zn=1;sigma_zn=0.033;zr=1.03;sigma_zr=0.03399;zv=1.04;sigma_zv=0.03432;zl=0.92;sigma_zl=0.03036;zw=1;sigma_zw=0.033;zx=1;sigma_zx=0.033;sigma_y=sigmacheng(zh,sigma_zh,ze,sigma_ze);y=zh*ze; sigma_y=sigmacheng(y,sigma_y,zt,sigma_zt);y=y*zt; sigma_y=sigmacheng(y,sigma_y,zb,sigma_zb); y=y*zb;sigma_x=sigmacheng(ka,sigma_ka,kv,sigma_kv);x=ka*kv; sigma_x=sigmacheng(x,sigma_x,khb,sigma_khb); x=x*khb; sigma_x=sigmacheng(x,sigma_x,kx,sigma_kx);x=x*kx;u=3.5;u=(u+1)/u;sigma_t=sigma_ft*u;t=ft*u;sigma_t=sigmachu(t,sigma_t,b,sigma_b);t=t/b;sigma_t=sigmachu(t,sigma_t,d1,sigma_d1); t=t/d1;sigma_c=sigmacheng(t,sigma_t,x,sigma_x); c=t*x;v=c;c=sqrt(sqrt(c*c-0.5*sigma_c*sigma_c));sigma_c=sqrt(v-sqrt(v*v-0.5*sigma_c*sigma_c));sigma_c=sigmacheng(c,sigma_c,y,sigma_y);c=c*y;sigma_sigmahlim=sigmacheng(sigmahlim,sigma_sigmahlim ,zn,sigma_zn);sigmahlim=sigmahlim*zn;sigma_sigmahlim=sigmacheng(sigmahlim,sigma_sigmahlim ,zr,sigma_zr);sigmahlim=sigmahlim*zr;sigma_sigmahlim=sigmacheng(sigmahlim,sigma_sigmahlim ,zv,sigma_zv);sigmahlim=sigmahlim*zv;sigma_sigmahlim=sigmacheng(sigmahlim,sigma_sigmahlim ,zl,sigma_zl);sigmahlim=sigmahlim*zl;sigma_sigmahlim=sigmacheng(sigmahlim,sigma_sigmahlim ,zw,sigma_zw);sigmahlim=sigmahlim*zw;sigma_sigmahlim=sigmacheng(sigmahlim,sigma_sigmahlim ,zx,sigma_zx);sigmahlim=sigmahlim*zx;R=sigmahlim-c;sigma_R=sigmaadd(sigma_sigmahlim,sigma_c);result=integral(R,sigma_R,0,R+100*sigma_R);cout<<result;return 0;}结果：齿面接触可靠度为0.982475程序2：基于齿根弯曲强度的可靠性#include <iostream>#include <cmath>using namespace std;#define PI 3.141592653double fun(double x,double miu,double sigma){return 1/(sqrt(2*PI)*sigma)*exp(-((x-miu)*(x-miu))/2/sigma/sigma);}double integral(double miu,double sigma,double a,double b){double s,h;int i;int N=abs(a-b)/0.001;s=(fun(a,miu,sigma)+fun(b,miu,sigma))/2.0;h=(b-a)/N;for(i=1;i<N;i++)s+=fun(a+i*h,miu,sigma);return(s*h);}double sigmaadd(double sigma_c,double sigma_d){return sqrt(sigma_c*sigma_c+sigma_d*sigma_d);}double sigmacheng(double a,double sigma_a,double b,double sigma_b){returnsqrt(a*a*sigma_b*sigma_b+b*b*sigma_a*sigma_a+sigma_b*sigma_b*sigma_a*sigma_a); }double sigmachu(double a,double sigma_a,double b,double sigma_b){return 1/b*sqrt((a*a*sigma_b*sigma_b+b*b*sigma_a*sigma_a)/(b*b+sigma_b*sigma_b)); }int main(){double ft,sigma_ft,ka,sigma_ka,kv,sigma_kv;double kfb,sigma_kfb,kx,sigma_kx,b,sigma_b;double mn,sigma_mn,result;double y,x,t,c,R,sigma_y,sigma_x,sigma_t,sigma_c,sigma_R;double yf,sigma_yf,ys,sigma_ys;double ye,sigma_ye,yb,sigma_yb,yst,sigma_yst;double sigmaflim,sigma_sigmaflim,ynt,sigma_ynt;double y1t,sigma_y1t,y2t,sigma_y2t,yx,sigma_yx;ft=34644;sigma_ft=519.66;ka=1;sigma_ka=0.033;kv=1.484;sigma_kv=0.1613;kfb=1.603;sigma_kfb=0.052899;kx=1.16;sigma_kx=0.03828;b=100;sigma_b=0.5;mn=4;sigma_mn=0.02;yf=2.36;sigma_yf=0.07788;ys=1.94;sigma_ys=0.06402;ye=0.715;sigma_ye=0.003575;yb=0.8;sigma_yb=0.004;yst=2.1;sigma_yst=0.0693;sigmaflim=310;sigma_sigmaflim=62;ynt=1;sigma_ynt=0.033;y1t=0.99;sigma_y1t=0.03267;y2t=1.065;sigma_y2t=0.035145;yx=1;sigma_yx=0.033;sigma_y=sigmacheng(yf,sigma_yf,ys,sigma_ys);y=yf*ys;sigma_y=sigmacheng(y,sigma_y,ye,sigma_ye);y=ye*y;sigma_y=sigmacheng(y,sigma_y,yb,sigma_yb); y=y*yb;sigma_x=sigmacheng(ka,sigma_ka,kv,sigma_kv);x=ka*kv;sigma_x=sigmacheng(x,sigma_x,kfb,sigma_kfb); x=x*kfb;sigma_x=sigmacheng(x,sigma_x,kx,sigma_kx);x=x*kx;sigma_t=sigmachu(ft,sigma_ft,b,sigma_b);t=ft/b;sigma_t=sigmachu(t,sigma_t,mn,sigma_mn);t=t/mn;sigma_sigmaflim=sigmacheng(sigmaflim,sigma_sigmaflim ,yst,sigma_yst);sigmaflim=sigmaflim*yst;sigma_sigmaflim=sigmacheng(sigmaflim,sigma_sigmaflim ,ynt,sigma_ynt);sigmaflim=sigmaflim*ynt;sigma_sigmaflim=sigmacheng(sigmaflim,sigma_sigmaflim ,y1t,sigma_y1t);sigmaflim=sigmaflim*y1t;sigma_sigmaflim=sigmacheng(sigmaflim,sigma_sigmaflim ,y2t,sigma_y2t);sigmaflim=sigmaflim*y2t;sigma_sigmaflim=sigmacheng(sigmaflim,sigma_sigmaflim ,yx,sigma_yx);sigmaflim=sigmaflim*yx;sigma_c=sigmacheng(t,sigma_t,y,sigma_y);c=t*y;sigma_c=sigmacheng(t,sigma_t,x,sigma_x);c=t*x;R=sigmaflim-c;sigma_R=sigmaadd(sigma_sigmaflim,sigma_c);result=integral(R,sigma_R,0,R+100*sigma_R);cout<<result;return 0;}结果：齿根弯曲疲劳强度可靠度为0.998602综上：齿轮的可靠度为0.982475。