模拟量与数字量的相互转换
- 格式:pptx
- 大小:573.64 KB
- 文档页数:15

![模拟量与数字量转换,电子技术[1]](https://uimg.taocdn.com/34f7f419168884868662d64a.webp)
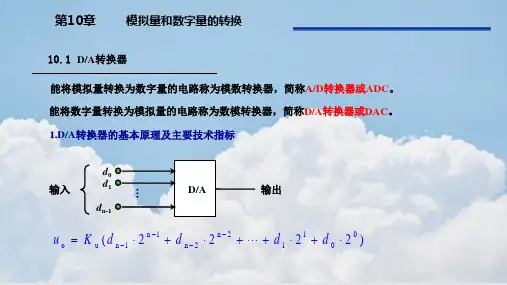

输入模拟量与输出数字量的计算公式在我们的电子世界里,输入模拟量与输出数字量之间有着神秘而有趣的关系,这背后藏着一套计算公式。
咱们先来说说啥是输入模拟量。
比如说,温度、压力、声音的强度,这些连续变化的量就是模拟量。
就拿温度来说吧,它可不是一下子从 0 跳到 10 度,而是能在 0 到 10 度之间平滑地变化。
而输出数字量呢,就像是我们在计算机里看到的 0 和 1 组成的数字。
比如说,温度传感器把连续变化的温度转变成计算机能处理的数字信号,这就是从模拟量变成了数字量。
那它们之间的计算公式到底是啥呢?一般来说,常用的公式是:数字量 = (模拟量 - 模拟量下限)×(数字量最大值 - 数字量最小值)÷(模拟量上限 - 模拟量下限) + 数字量最小值咱来举个例子哈。
假设我们有一个温度传感器,它能测量的温度范围是 0 到 100 度(这就是模拟量的范围),而对应的数字量范围是 0到 1023 。
现在测到的温度是 50 度,那按照公式算一下:数字量 = (50 - 0)×(1023 - 0)÷(100 - 0) + 0算出来大概是 511.5 ,因为数字量得是整数,所以就约等于 512 。
还记得我之前参加过一个电子小制作的活动。
我们要做一个能显示环境湿度的小装置。
在这个过程中,就得搞清楚湿度这个模拟量怎么变成能在屏幕上显示的数字量。
当时可把我难坏了,对着那一堆公式和数据,脑袋都大了几圈。
我就不停地测试,调整参数,反复计算。
有好几次都算错了,显示出来的湿度数值完全不对,要么超高,要么超低,就像个调皮的孩子在跟我开玩笑。
但我没放弃,继续琢磨,终于算出了正确的结果。
当看到那个小装置准确地显示出环境湿度的时候,心里那叫一个美呀!这就像是解开了一道神秘的谜题,找到了通往数字世界和现实世界的桥梁。
其实啊,输入模拟量与输出数字量的计算公式在很多地方都有用。
比如在工业自动化控制中,要精确控制机器的运行,就得靠这个公式把各种模拟量转化成数字量,让计算机能明白该怎么做。



模拟量转数字量万能公式在咱们的科技世界里,有一个特别神奇的概念,叫做“模拟量转数字量”。
这玩意儿听起来好像挺复杂,挺高大上的,但其实啊,它就像我们学骑自行车,一开始觉得难,掌握了窍门之后就会发现,也就那么回事儿。
我记得有一次,我在一个电子实验室里,看到一群学生正在为这个问题抓耳挠腮。
他们面前摆着各种仪器,眼神里充满了困惑和迷茫。
其中有个叫小明的同学,那着急的样子,就像是热锅上的蚂蚁。
咱们先来说说啥是模拟量。
简单来讲,模拟量就像是一条连续不断的河流,它的数值可以在一定范围内任意变化,没有固定的间隔或者台阶。
比如说,温度、压力、声音的强弱,这些都是模拟量。
那数字量呢?数字量就像是一级一级的台阶,它的数值是离散的,只能是一些特定的值。
比如说,咱们电脑里存储的数字 0 和 1 ,就是典型的数字量。
那为啥要把模拟量转成数字量呢?这就好比我们要把一条流淌的河,变成一段一段的水池子,这样我们的电脑啊、电子设备啊,才能更好地处理和理解这些信息。
这时候,咱们就得提到那个传说中的“万能公式”啦!其实啊,它并不是一个真正像数学公式那样写在纸上就能套用的式子,而是一套方法和思路。
比如说,咱们要测量一个温度。
温度是模拟量,那怎么转成数字量呢?首先,咱们得确定一个测量的范围,比如说 0 到 100 度。
然后,我们把这个范围分成很多小的区间,假设分成 1000 个区间。
每个区间就代表一个数字值。
这时候,我们用一个传感器来测量温度,传感器会把温度的变化转化成电信号。
然后通过一个叫做 ADC(模数转换器)的东西,把这个电信号转换成数字信号。
这个 ADC 就像是一个神奇的魔法盒子,能把模拟的东西变成数字的。
但是这里面可有点小讲究哦。
比如说,这个 ADC 的精度,精度越高,转换出来的数字量就越准确。
就像你用一把刻度很精细的尺子去测量东西,肯定比用一把粗糙的尺子准得多。
再比如说,采样频率也很重要。
采样频率就像是你拍照的快门速度,速度越快,就能捕捉到更多的细节。


信号的变换需要经过以下过程:物理量-传感器信号-标准电信号-A/D转换-数值显示。
声明:为简单起见,我们在此讨论的是线性的信号变换。
同时略过传感器的信号变换过程。
假定物理量为A,范围即为A0-Am,实时物理量为X;标准电信号是B0-Bm,实时电信号为Y;A/D转换数值为C0-Cm,实时数值为Z。
如此,B0对应于A0,Bm对应于Am,Y对应于X,及Y=f(X)。
由于是线性关系,得出方程式为Y=(Bm-B0)*(X-A0)/(Am-A0)+B0。
又由于是线性关系,经过A/D转换后的数学方程Z=f(X)可以表示为Z=(Cm-C0)*(X-A0)/(Am-A0)+C0。
那么就很容易得出逆变换的数学方程为X=(Am-A0)*(Z-C0)/(Cm-C0)+A0。
方程中计算出来的X就可以在显示器上直接表达为被检测的物理量。
5、PLC中逆变换的计算方法以S7-200和4-20mA为例,经A/D转换后,我们得到的数值是6400-32000,及C0=6400,Cm=32000。
于是,X=(Am-A0)*(Z-6400)/(32000-6400)+A0。
例如某温度传感器和变送器检测的是-10-60℃,用上述的方程表达为X=70*(Z-6400)/25600-10。
经过PLC的数学运算指令计算后,HMI可以从结果寄存器中读取并直接显示为工程量。
用同样的原理,我们可以在HMI上输入工程量,然后由软件转换成控制系统使用的标准化数值。
在S7-200中,(Z-6400)/25600的计算结果是非常重要的数值。
这是一个0-1.0(100%)的实数,可以直接送到PID指令(不是指令向导)的检测值输入端。
PID指令输出的也是0-1.0的实数,通过前面的计算式的反计算,可以转换成6400-32000,送到D/A端口变成4-20mA输出。
1.自己写转换程序。
2.需要注意你的模拟量是单极性的还是双极性的。
函数关系A=f(D)可以表示为数学方程:A=(D-D0)×(Am-A0)/(Dm-D0)+A0。

创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*信号的变换需要经过以下过程:物理量-传感器信号-标准电信号-A/D转换-数值显示。
声明:为简单起见,我们在此讨论的是线性的信号变换。
同时略过传感器的信号变换过程。
假定物理量为A,范围即为A0-Am,实时物理量为X;标准电信号是B0-Bm,实时电信号为Y;A/D转换数值为C0-Cm,实时数值为Z。
如此,B0对应于A0,Bm对应于Am,Y对应于X,及Y=f(X)。
由于是线性关系,得出方程式为Y=(Bm-B0)*(X-A0)/(Am-A0)+B0。
又由于是线性关系,经过A/D转换后的数学方程Z=f(X)可以表示为Z=(Cm-C0)*(X-A0)/(Am-A0)+C0。
那么就很容易得出逆变换的数学方程为X=(Am-A0)*(Z-C0)/(Cm-C0)+A0。
方程中计算出来的X就可以在显示器上直接表达为被检测的物理量。
5、PLC中逆变换的计算方法以S7-200和4-20mA为例,经A/D转换后,我们得到的数值是6400-32000,及C0=6400,Cm=32000。
于是,X=(Am-A0)*(Z-6400)/(32000-6400)+A0。
例如某温度传感器和变送器检测的是-10-60℃,用上述的方程表达为X=70*(Z-6400)/25600-10。
经过PLC的数学运算指令计算后,HMI可以从结果寄存器中读取并直接显示为工程量。
用同样的原理,我们可以在HMI上输入工程量,然后由软件转换成控制系统使用的标准化数值。
在S7-200中,(Z-6400)/25600的计算结果是非常重要的数值。
这是一个0-1.0(100%)的实数,可以直接送到PID指令(不是指令向导)的检测值输入端。
PID指令输出的也是0-1.0的实数,通过前面的计算式的反计算,可以转换成6400-32000,送到D/A端口变成4-20mA输出。
1.自己写转换程序。
