模拟量和数字量的转换-经典

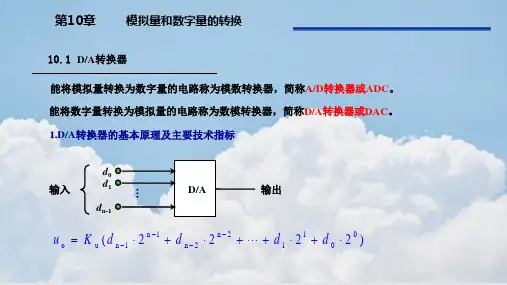
数字量转换模拟量公式摘要：1.数字量转换模拟量概述2.数字量与模拟量的关系3.数字量转换模拟量的公式4.公式应用实例5.总结与建议正文：在前文《数字量转换模拟量公式》中，我们了解了数字量和模拟量的基本概念，以及它们在实际应用中的重要性。

为了帮助大家更好地理解和掌握数字量转换模拟量的方法，本文将详细介绍数字量与模拟量之间的关系，并提供一个实用的转换公式。

首先，我们来回顾一下数字量和模拟量的定义。

数字量是指可以用整数或浮点数表示的量，通常用于计算机处理和存储信息。

而模拟量是指连续变化的物理量，例如温度、压力等，它们可以通过传感器或其他测量设备转换为数字信号。

数字量与模拟量之间的关系密切，数字量往往是模拟量通过一定方式转换得到的。

在实际应用中，我们需要将模拟量转换为数字量进行处理，或者将数字量转换回模拟量以满足设备或系统的需求。

这就涉及到数字量转换模拟量的关键步骤——公式应用。

为了方便理解和计算，我们可以将数字量转换模拟量的过程表示为一个公式：模拟量= 数字量× 转换系数+ 偏置其中，转换系数和偏置是根据实际应用场景和设备要求来确定的。

例如，在某些传感器中，数字量的每个单位可能对应着模拟量的某个固定范围，这时转换系数就是传感器灵敏度，而偏置则是传感器零点。

接下来，我们通过一个实例来说明如何使用这个公式进行数字量到模拟量的转换。

假设某个温度传感器输出的数字量为1234，传感器灵敏度为10，零点为-50，求温度传感器的实际温度。

根据公式，我们可以得到：实际温度= 1234 × 10 + (-50) = 12840 - 50 = 12790因此，该温度传感器的实际温度为12790。

最后，总结一下数字量转换模拟量的方法和注意事项：1.了解数字量和模拟量的基本概念，明确它们之间的关系。

2.确定合适的转换系数和偏置，以便进行准确的数字量转换。

3.熟练掌握公式应用，灵活应对不同场景和设备要求。

4.在实际应用中，注意传感器和设备的调试与校准，确保数字量转换结果的准确性。

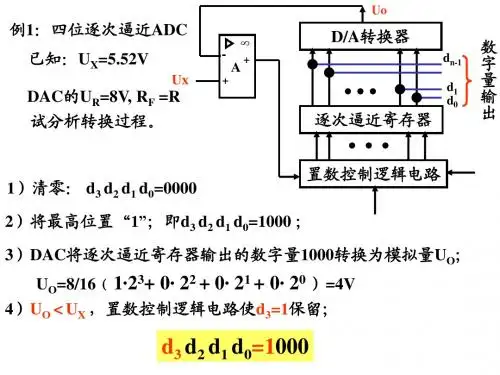
置数控制逻辑电路逐次逼近寄存器D/A 转换器 ++-A Ux 数字量输出Uod 0d 1d n-1例1：四位逐次逼近ADC已知：U X =5.52VDAC 的U R =8V , R F =R试分析转换过程。

1）清零：d 3 d 2 d 1 d 0=00002）将最高位置“1”；即d 3 d 2 d 1 d 0=1000 ；3）DAC 将逐次逼近寄存器输出的数字量1000转换为模拟量U O ；4）U O <U X ，置数控制逻辑电路使d 3=1保留；U O =8/16（1·23+ 0· 22+ 0· 21+ 0· 20 ）=4Vd 3 d 2 d 1 d 0=10005）将d2置“1”；即d3 d2 d1 d0=1100 ；6）DAC将逐次逼近寄存器输出的数字量1100转换为模拟量U O；U O=8/16（1·23+ 1· 22+ 0· 21+ 0· 20 ）=6V7）U O >U X，置数控制逻辑电路使d2=1去掉，使d2=0；d3 d2d1 d0=10008）将d1置“1”；即d3 d2 d1 d0=1010 ；9）DAC将逐次逼近寄存器输出的数字量1010转换为模拟量U O；U O=8/16（1·23+ 0· 22+ 1· 21+ 0· 20 ）=5V10）U O <U X，置数控制逻辑电路使d1=1保留；d3 d2 d1d0=101011）将d0置“1”；即d3 d2 d1 d0=1011；12）DAC将逐次逼近寄存器输出的数字量1011转换为模拟量U O；U O=8/16（1·23+ 0· 22+ 1· 21+ 1· 20 ）=5.5V10）U O <U X，置数控制逻辑电路使d0=1保留；d3 d2 d1d0=1011ADCU X=5.52V d3 d2 d1d0=1011转换误差=0.02V，输出位数越多，误差越小。

信号的变换需要经过以下过程：物理量－传感器信号－标准电信号－A/D转换－数值显示。

声明：为简单起见，我们在此讨论的是线性的信号变换。

同时略过传感器的信号变换过程。

假定物理量为A，范围即为A0－Am，实时物理量为X；标准电信号是B0－Bm，实时电信号为Y；A/D转换数值为C0-Cm，实时数值为Z。

如此，B0对应于A0，Bm对应于Am，Y对应于X，及Y=f(X)。

由于是线性关系，得出方程式为Y=(Bm-B0)*(X-A0)/(Am-A0)+B0。

又由于是线性关系，经过A/D转换后的数学方程Z=f(X)可以表示为Z=(Cm-C0)*(X-A0)/(Am-A0)+C0。

那么就很容易得出逆变换的数学方程为X=(Am-A0)*(Z-C0)/(Cm-C0)+A0。

方程中计算出来的X就可以在显示器上直接表达为被检测的物理量。

5、PLC中逆变换的计算方法以S7-200和4－20mA为例，经A/D转换后，我们得到的数值是6400－32000，及C0=6400，Cm=32000。

于是，X=(Am-A0)*(Z-6400)/(32000-6400)+A0。

例如某温度传感器和变送器检测的是-10－60℃，用上述的方程表达为X=70*(Z-6400)/25600-10。

经过PLC的数学运算指令计算后，HMI可以从结果寄存器中读取并直接显示为工程量。

用同样的原理，我们可以在HMI上输入工程量，然后由软件转换成控制系统使用的标准化数值。

在S7-200中，(Z-6400)/25600的计算结果是非常重要的数值。

这是一个0－1.0（100％）的实数，可以直接送到PID指令（不是指令向导）的检测值输入端。

PID指令输出的也是0－1.0的实数，通过前面的计算式的反计算，可以转换成6400－32000，送到D/A端口变成4－20mA输出。

1.自己写转换程序。

2.需要注意你的模拟量是单极性的还是双极性的。

函数关系A＝f（D）可以表示为数学方程：A＝（D－D0）×（Am－A0）／（Dm－D0）＋A0。

数字量转换模拟量公式数字量转换模拟量是一种常见的电子技术应用，广泛应用于工业自动化控制、仪器仪表以及通讯等领域。

该模拟量转换公式用于将数字信号转换为模拟信号，将数字量的离散值转换为连续的模拟量输出。

下面将介绍数字量转换模拟量的基本原理和常见的转换方法。

一、数字量转换模拟量的基本原理数字量转换模拟量的基本原理是利用数电电路中的数字信号处理技术，将离散的数字信号转换为连续的模拟信号。

数字信号是由0和1组成的离散信号，而模拟信号是连续的变化信号。

数字量转换模拟量的基本原理可以简单地描述为：将数字信号按照一定的规则映射到模拟信号的幅度范围内。

这个规则可以通过公式来表示，公式中包含了数字信号和模拟信号之间的转换关系。

二、数字量转换模拟量的常见方法数字量转换模拟量的方法有很多种，根据具体的需求和应用场景可以选择不同的转换方法。

下面介绍几种常见的数字量转换模拟量的方法。

1. DAC转换DAC（Digital to Analog Converter）是一种常见的数字量转换模拟量的方法。

DAC通过将数字信号转换为相应的模拟信号输出，可以实现数字量到模拟量的转换。

DAC转换的原理是根据输入的数字信号，通过一系列的运算和控制，将数字信号转换为相应的模拟信号输出。

2. PWM调制PWM（Pulse Width Modulation）是一种常见的数字量转换模拟量的方法。

PWM通过改变脉冲信号的占空比，来实现数字信号到模拟信号的转换。

PWM转换的原理是将数字信号转换为一系列的脉冲信号，通过改变脉冲信号的占空比来实现模拟信号的变化。

3. Sigma-Delta转换Sigma-Delta转换是一种高精度的数字量转换模拟量的方法。

Sigma-Delta转换的原理是通过过采样和噪声抑制技术，将数字信号转换为模拟信号。

Sigma-Delta转换的特点是精度高、抗干扰能力强，广泛应用于音频和视频信号的转换。

三、数字量转换模拟量的应用场景数字量转换模拟量广泛应用于工业自动化控制、仪器仪表以及通讯等领域。