当前位置：文档之家 › 07温度应力装配应力 材料力学 第四版 刘鸿文 课件

07温度应力装配应力 材料力学 第四版 刘鸿文 课件

  • 格式：ppt
  • 大小：169.00 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

7材料力学课件(刘鸿文)

7材料力学课件(刘鸿文)

二、约束扭转：杆件扭转时，横截面的翘曲受到限制，相邻 约束扭转： 截面翘曲程度不同。 若杆的两端受到约束而不能自由翘曲，则相邻两横截 若杆的两端受到约束而不能自由翘曲， 面的翘曲程度不同，这将在横截面上引起附加的正应力。 面的翘曲程度不同，这将在横截面上引起附加的正应力。 这一情况称为 约束扭转. 约束扭转.
三、矩形杆横截面上的剪应力: 矩形杆横截面上的剪应力: 1. 剪应力分布如图： （角点、形心、长短边中点） b
τ max
h
τ1
注意！ h ≥ b
T
2. 最大剪应力及单位扭转角
T max τ max = Wt
b
其中： W =
t
β b3
max
τ 1 = ντ
τ max τ1
注意！ h≥ b
h
T θ= , GI t
， m2 = 955 N•m ， m3 = 637 N • m。截面 A与截面 B、C之间的 m。 距离分别为 lAB = 300 mm 和 lAC = 500 mm。轴的直径d = 70 mm, mm。轴的直径d 钢的剪切弹性模量为 G = 80 GPa。试求截面 C 对截面 B 的相对 GPa。 扭转角。 扭转角。
T =
W1 t
(b)
l
T =
W2 t
l
d 2 D2
T
W1 t
T =
W2 t
Q Wt1 =Wt2
π 1 d3 W1 = t 16 3 π 2 ( −α4 ) D 1 W2 = t 16
因此
3 πd1
(a)
d1
l
(b)
d 2 D2
16
=
π1−α4 ) 2
16
l

刘鸿文主编(第4版) 高等教育出版社《材料力学》课件全套

刘鸿文主编(第4版) 高等教育出版社《材料力学》课件全套
解： 用截面m-m将钻床截为两部分，取上半 部分为研究对象，
受力如图：
列平衡方程:
M
Y 0 FN P
Mo(F) 0
FN
Pa M 0
M Pa
目录
§1.4 内力、截面法和应力的概念
为了表示内力在一点处的强度，引入内力集度,
即应力的概念。
F A
pm
F A
—— 平均应力
C
p lim F A0 A
径20mm的圆截面杆，水平杆CB为 15×15的方截面杆。
B 解：1、计算各杆件的轴力。 （设斜杆为1杆，水平杆为2杆）
F 用截面法取节点B为研究对象
Fx 0 FN1 cos 45 FN2 0
x
Fy 0 FN1 sin 45 F 0
FN1 28.3kN
FN 2 20kN
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
m
F m
F
FN
FN
Fx 0
FN F 0 FN F
2、轴力：截面上的内力
F
由于外力的作用线
与杆件的轴线重合，内
力的作用线也与杆件的
轴线重合。所以称为轴
力。 F 3、轴力正负号：
拉为正、压为负
4、轴力图：轴力沿杆 件轴线的变化
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
例题2.1
A
F1
若：构件横截面尺寸不足或形状
不合理,或材料选用不当
___ 不满足上述要求,
不能保证安全工作.
若：不恰当地加大横截面尺寸或
选用优质材料
___ 增加成本,造成浪费
}均 不 可 取
研究构件的强度、刚度和稳定性,还需要了解材料的力学性能。因此在 进行理论分析的基础上，实验研究是完成材料力学的任务所必需的途径和 手段。

刘鸿文主编-材料力学课件

刘鸿文主编-材料力学课件

各向同性假设
总结词
各向同性假设认为材料在不同方向上具有相同的性质 和行为。
详细描述
各向同性假设是材料力学中的另一个重要假设。它意味 着材料在不同方向上具有相同的性质，如弹性模量、泊 松比等。这一假设使得我们可以用统一的数学模型来描 述材料的性质和行为，简化计算过程。在实际应用中， 对于一些各向同性较好的材料，可以采用统一的标准来 近似获得其整体性质。需要注意的是，各向同性材料并 不是指所有方向上的性质都完全相同，而是在一定范围 内可以近似认为各向同性。
机械零件设计
材料力学在机械领域中应用于各 种机械零件的设计，如轴、轴承
、齿轮等。
设备强度分析
对机械设备的强度进行分析，确保 设备在各种工况下的安全运行。
疲劳寿命预测
利用材料力学知识，预测机械零件 的疲劳寿命，提高设备的使用寿命 。
航空航天领域
飞行器结构分析
材料力学在航空航天领域 中应用于飞行器的结构分 析，确保飞行器的安全性 和稳定性。
详细描述
弹性力学理论是材料力学的基本理论之一，主要研究材料在弹性范围内受力时的变形和内力关系。该 理论基于胡克定律，即材料在弹性范围内受力时发生的形变与外力成正比，并引入了应变和应力等概 念来描述材料的变形和受力情况。
塑性力学理论
总结词
描述材料在超过弹性极限后发生塑性形 变时的应力-应变关系。
VS
根据船舶的工作环境和要求，选择具 有优良力学性能的材料。
05
材料力学的未来发展
新材料的研发
高强度轻质材料
如碳纤维复合材料、钛合金等， 在航空、汽车、体育器材等领域
有广泛应用前景。
智能材料
如形状记忆合金、压电陶瓷等， 具有自适应、自修复等特性，可 用于制造智能传感器、执行器等

材料力学ppt(刘鸿文第四版含课后答案)

材料力学ppt(刘鸿文第四版含课后答案)

l1
A' l3
(3) 物理关系
A
l1

N1l
E1A1 cos
l1 l2 A' l3
(1) 静平衡方程
N1 N2
(1)
N3 2N1 cos P 0 (2)
(2) 变形协调方程 l1 l源自 l3 cos (3)(3) 物理关系
l1

N1l
E1A1 cos

0.52 104 (m)
AB杆的变形
lAB lBD lCD lAC 1.05104(m)
例 2 (书例2. 7) 已知： BC杆: d=20mm, BD杆: 8号槽钢。[]= 160 MPa, E=200GPa, P=60kN。 求：校核强度及B点位移。 解：(1) 求轴力
Al
l Nl Pl 胡克定律的
EA EA
另一种形式
EA 抗拉(或抗压)刚度
注意：上式只在应力不超过比例极限时成立。
推广: (1) 阶梯轴
l Nili
Ei Ai
(2) 变截面轴
l

l
N ( x) EA(x)
dx
l1
l2
l3
A1
A2
A3
x
N(x)+dN(x)
N(X)
应力 A2 1024.8106 m2
1

N1 A1
143MPa
[ ] 160MPa
2

N2 A2

73.2 MPa
[ ] 160MPa
(3) 计算杆的变形
BC杆变形
l1

BB1
N1l1 EA1

材料力学刘鸿文第4版(二)PPT课件

材料力学刘鸿文第4版(二)PPT课件

②悬臂梁
21.07.2020
q(x)— 分布力
6
③外伸梁
q — 均布力
P — 集中力
5. 静定梁与超静定梁
静定梁：由静力学方程可求出支反力，如上述三种基本 形式的静定梁。
超静定梁：由静力学方程不可求出支反力或不能求出全 部支反力。
21.07.2020
7
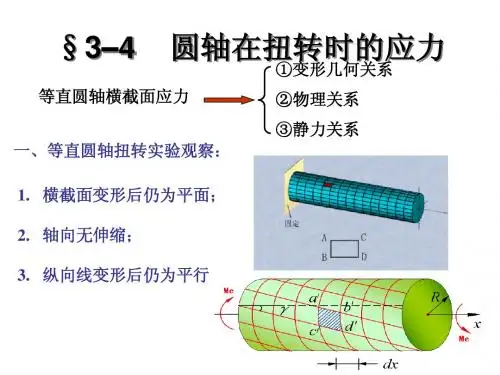
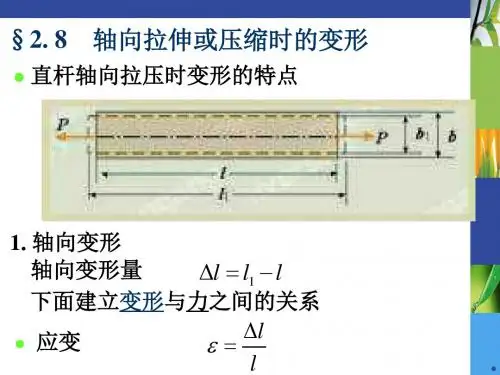
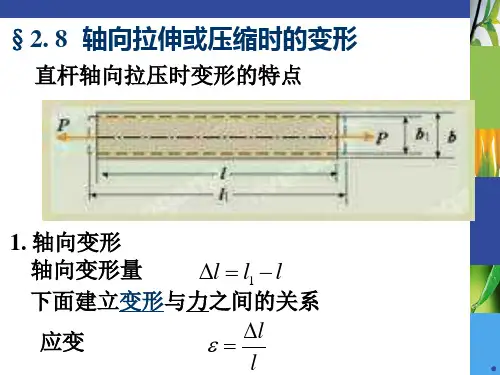
§4-3 剪力与弯矩
shearing force and bending moment
2. Q > 0, M走上坡路; Q < 0, M走下坡路. Q 0, M 走平路; Q = 0处, M有极值
3. q > 0, M 为极小值; q < 0, M 为极大值.
利用平衡关系, 结合截面法, 可以很快地画出 QM 图.
例4-9 (P128) 求作 QM 图
叠加法: 小变形情况下, 内力与外力成线性关系, 内力图可以叠加.
结果正确.
(2)求内力: 第一段:
第二段：
m Q(x1) RA l ,
M(x1)
m l
x1,
m Q(x2) RB l ,
m M(x2) l x2,
0 x1 a. 0 x2 b.
(3) 危险截面在 Q 及 M 绝对值最大处. (4)标出 Qmax 及 Mmax 的大小及位置.
m Q(x1) RA l ,
dx2
21.07.2020
13
§4-5 载荷集度、剪力和弯矩间的关系
Relations between q, Q and M
微分规则： dQ(x) q(x), dM(x) Q(x),
dx
dx
由微分规则可见，当 x 轴选择向右时：
d2M(x) q(x).

材料力学(刘鸿文版)全套课件 PPT

材料力学(刘鸿文版)全套课件 PPT

850 750 650 550
104
105
106
107
108
N
从图可以得出三点结论：
(1)对于疲劳，决定寿命的 最重要因素是应力幅 。
(2)材料的疲劳寿命N 随应力幅 的增大而减小。
(3)存在这样一个应力幅，低于该应力幅，疲劳破坏不会发生，该应力幅
称为疲劳极限，记为 -1 。
目录
对于铝合金等有色金属，其S-N曲线没有明显的水平部分，一般规定
Δ
max
m in
O t
目录
通常用以下参数描述循环应力的特征
(1)应力比 r
r min max
r = -1 ：对称循环 ； r = 0 ：脉动循环 。
r < 0 ：拉压循环 ； r > 0 ：拉拉循环 或压压循环。
(2)应力幅
max min
(3)平均应力 m
B L
解： ⑴ 弯矩方程
F
A
M (x) M e Fx
Me
⑵ 变形能
V

L
M 2 (x) dx 2EI
L
1 2EI
(M
e
Fx)2 dx

M
2 e
L

M e FL2

F 2 L2
2EI 2EI 6EI
B L
F
⑶ 当F和M0分别作用时
A M0
V 1

MeL 2EI
F 2 L3 V 2 6EI
例：试求图示悬臂梁的应变能，并利用功
能原理求自由端B的挠度。
F
解：
l
x
M (x) F x
V

材料力学ppt(刘鸿文第四版含课后答案)

材料力学ppt(刘鸿文第四版含课后答案)
V
应力分布均匀 均匀时 应力分布均匀时
N Al N l U = uV = V = = 2 2E 2EA 2EA
Nl 推广到多杆系统 U = ∑ i=1 2E A i i
1 由能量守恒原理 U =W= P∆l 2 2 n 有 1 Ni li P∆l = ∑ 2 i=1 2E A i i
n 2 i i
关于静不定的基本概念
静定问题
静不定问题 —— 静不定次数 —— 多余约束 ——
求解静不定问题的基本方法
力的平衡关系。 静力平衡方程 －力的平衡关系。 变形与约束的协调关系。 变形协调方程 － 变形与约束的协调关系。 力与变形的关系。 物理关系 － 力与变形的关系。
例 1 (书p.50) 书 已知：1、2杆相同，抗拉 杆相同， 已知： 、 杆相同 刚度为E 刚度为 1A1 , 3杆的抗拉 杆的抗拉 长为l 角 刚度为E 刚度为 3A3 , 长为 , α角。 各杆的内力。 求：各杆的内力。 解： 静不定的次数？ 静不定的次数？
(2) 变形协调方程 (3) 物理关系
∆l1 = ∆l2 = ∆l3 cosα (3) N1l N3l ∆l1 = ∆l3 = E1A cosα E3 A 1 3
(4)
物理关系代入变形协调方程
N1l N3l = cosα E A cosα E3 A 1 1 3
与平衡方程联立，可解出 与平衡方程联立，可解出:
D
C
B
2 l N2
3
1
αα
A P y N3
αα
∑X = 0 N1 sin α − N2 sinα = 0 N1 = N2 ∑Y = 0 N3 +2N1 cosα − P = 0
N1
x
P

绪论材料力学第四版刘鸿文课件分析

绪论材料力学第四版刘鸿文课件分析
材料力学
主讲：赵玉萍
《材料力学》课程基本情况 ：
1.学时：80学时（包含：8学时实验） 2.成绩比例：平时成绩20%
期终考试80%
3.上课要求：不迟到、带笔、带练习本。 4.参考书目：图书馆四楼“工业技术阅览室”
索书号“TB301”
第1章 绪论
1.1 材料力学的任务 一、材料力学的研究对象：构件中的杆件、零件 1.构件的分类：
附2：学好本课程的关键
1.良好的静力学基础。 2. 正确对构件进行受力分析；
选用正确的理论进行计算。 3.紧跟老师讲课的进程，循序渐进。 4.多做练习题。
1、字体安装与设置
2、替换模板
如果您对PPT模板中的字体风格不满意，可进行批量替换，一次性更改各页面字体。 1. 在“开始”选项卡中，点击“替换”按钮右侧箭头，选择“替换字体”。（如下图）
一、构件的内力 由于外部原因引起构件内部各部 分之间的相互作用力。
F1
F3
外力 物体外部 变形
引起
内力 物体内部
F2
Fn
1.内力必须满足平衡条件
作用在变形体上 的外力相互平衡
内力与外力平衡 内力与内力相等
F1
F2
F
假想截面 F3
F1
F2
F
分布内力 F3
二、求内力的方法→截面法
F5
m F4
F1
F2
1.均匀、连续性假设
2.各向同性假设
3.小变形假设
1、材料的均匀、连续性假设 是指材料内部没有空隙；是指材料的性 质各处都一样。
球墨铸铁的显微组织：微观不连续， 不均匀 ，宏观连续均匀。
2、材料的各向同性假设 材料沿不同方向具有相同的力学性质。

刘鸿文版材料力学课件全套4ppt课件

刘鸿文版材料力学课件全套4ppt课件

解：（1）计算横截面的形心、 面积、惯性矩
F 350 F
F 350
M
y1 z0 y
FN
z1
150
A 15000mm2 z0 75mm z1 125 mm I y 5.31107 mm4
50 （2）立柱横截面的内力
FN F
M F 350 75103
50
150
425F 103 N m
10-1
压弯组合变形
目录
§8-1 组合变形和叠加原理
组合变形工程实例
拉弯组合变形
目录
§8-1 组合变形和叠加原理
组合变形工程实例
弯扭组合变形
目录
§8-1 组合变形和叠加原理
叠加原理
构件在小变形和服从胡克定理的条件下， 力的独立性原理是成立的。即所有载荷作用 下的内力、应力、应变等是各个单独载荷作 用下的值的叠加
r4
M8-4 扭转与弯曲的组合
r3
M 2 T 2
W
W d 3
32
d 3 32
M2 T2
3
32
1762 3002 100106
32.8103 m 32.8mm
目录
小结
1、了解组合变形杆件强度计算的基本方法 2、掌握斜弯曲和拉（压）弯组合变形杆件
0 －极限切应力，由单向拉伸实验测得
0 s /2
目录
7-11 四种常用强度理论
最大切应力理论（第三强度理论）
屈服条件 强度条件
1
3
s
ns
低碳钢拉伸
低碳钢扭转
目录
7-11 四种常用强度理论
最大切应力理论（第三强度理论） 实验表明：此理论对于塑性材料的屈服破坏能够得到 较为满意的解释。并能解释材料在三向均压下不发生

材料力学ppt刘鸿文版

材料力学ppt刘鸿文版
目录
§2.7 失效、安全因数和强度计算
例题2.5
AC为50×50×5的等边角钢，AB为10 号槽钢，〔σ〕=120MPa。确定许可载荷F。
解：1、计算轴力（设斜杆为1杆，水平杆 为2杆）用截面法取节点A为研究对象 Fx 0 FN1 cos FN 2 0
F
y
0
FN1 sin F 0
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
例题2.1
A
1 B
11=10kN；F2=20kN； F3=35kN；F4=25kN;试画 出图示杆件的轴力图。
F1 F1 F1
FN kN
F3
3
F4
解：1、计算各段的轴力。 AB段
FN1 FN2 F2
F F
x
x
0
FN1 F1 10kN
在图示结构中，设横梁AB的 变形可以省略，1，2两杆的横截 面面积相等，材料相同。试求1， 2两杆的内力。 解： 1、列出独立的平衡方程
1
例题2.8
2
l

3F 2FN 2 cos FN1 0
2、变形几何关系
A
B
a
l1
a
l2
a
l2 2l1 cos
3、物理关系
4、补充方程
b ｝ F n
例题3-2
FS
h
nn
n
b
l
O Me
Fbs Abs bs
d
O
Me
0.5h
(a)
(b)
nF n S
(c)
目录
§2-13 剪切和挤压的实用计算
解：（1）校核键的剪切强度
Fs A bl d d 由平衡方程 M o 0 得 Fs bl M e

刘鸿文版材料力学(全套)

刘鸿文版材料力学(全套)
材料力学
刘鸿文主编(第4版) 高等教育出版社
精品课件
目录
第一章 绪论
精品课件
目录
第一章 绪论
§1.1 材料力学的任务 §1.2 变形固体的基本假设 §1.3 外力及其分类 §1.4 内力、截面法及应力的概念 §1.5 变形与应变 §1.6 杆件变形的基本形式
精品课件
目录
§1.1 材料力学的任务
精品课件
目录
§1.2 变形固体的基本假设
3、各向同性假设： 认为在物体内各个不同方向的力学性能相同
（沿不同方向力学性能不同的材料称为各向异性 材料。如木材、胶合板、纤维增强材料等）
4、小变形与线弹性范围
A
认为构件的变形极其微小，
Байду номын сангаас比构件本身尺寸要小得多。
如右图，δ远小于构件的最小尺寸，
所以通过节点平衡求各杆内力时，把支
x方向的平均应变：
xm
s x
L
o M x
x+s
M'
N'
N
x
切应变（角应变）
M点处沿x方向的应变： M点在xy平面内的切应变为：
x
lim
x0
s x
g lim(LMN)
2 MN0
M L0
类似地，可以定义 y , z ,g 均为无量纲的量。
精品课件
目录
§1.5 变形与应变
例 1.2
c
已知：薄板的两条边
F F
FN
m m
FN
2、轴力：截面上的内力
F
由于外力的作用线
与杆件的轴线重合，内
力的作用线也与杆件的
轴线重合。所以称为轴
力。 F 3、轴力正负号：

[工学]材料力学课件第四版刘鸿文_OK

[工学]材料力学课件第四版刘鸿文_OK
B 例 6--9 求中点C的挠度。
分析：本题有二种解法
12
q A
c L qdx A c x L dx
q
A c L
一、将qdx看成集中力作用在距原点为x
B
处。用p190（9）式。
l
2 qx(3l 2 4x2 )dx
fl
2
0
48EJ
B
q 48EJ
3l 2 x2 (
2
x4)
l
2 0
BA +
ql 4 3 1 1 5ql 4
m ml
EJ
pl pl
2
fb
fd
d
l 4
fbd
48
fbd
p ( l )3 24 3EJ
pl 3
384EJ
d
c
cd
0
pl 2 2EJ2
ml EJ2
3 pl 2
12816EJ
fd
fc
c
l 4
fcd
0 0 l ml2 4 2EJ 2
pl3 3EJ 2
pl ( l )2 p ( l )3 8 4 2 4
8
(
)
1 3k
k1
k
3ql
as k k1 , k1 0 Rb 8
k as k k1 , k1 Rb 0 Reactions at point B can not exceed the range
通常结构的刚度介于二者之间，因此B点反力不能超过这个范围
Compare internal force and deformation
Equivalent force system
x
a
x a

07应力应变分析--材料力学(刘鸿文)

07应力应变分析--材料力学(刘鸿文)

x
切应力以企图使微体沿顺时 针方向旋转者为正； 倾角a ：自轴x开始逆时针
y
转向为正，反之为负。
2013-8-7
19
n
x
a
xy yx
Fn 0
Ft 0
a y
a
t
a
dA
dAsina
adA ＋（xy dA cosa）sina－（x dAcosa）cosa＋ （yxdA sina）cos a－（ydA sina）sina＝0
a 1.33MPa
max 42.4MPa
a 0 31.72
min 2.4MPa
a 0 90 121.7224
max 42.4MPa
a 0 31.72
得到：
min 2.4MPa
a 0 90 121.72
1
x
a0
3
1 42.4MPa
y
y
yx
yx
xy
x
x
y
2013-8-7
xy
x
纯剪应力状态 ( Shearing State of Stresses )
9
三向应力状态：三个主应力都不为零； 也称空间应力状态( Three-Dimensional State of Stresses )
yz zy
y yx
n
1 3
③主应力大小：
yx
x
a xy
n
x
max
min
1 1 2 （ x y ) ( x y ) 2 4 xy 2 2
y
④由max、、min作用方位（与两个a0如何对应） ⑥
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
B
1 LC 5
15kN
4 L 5
A
2.11
温度应力和装配应力
1.什么是温度应力？ 1.什么是温度应力？ 什么是温度应力 例.图示等直杆AB。长度为L，横截面面积为A, 长度为L 横截面面积为A, 弹性模量E, E,线膨胀系数 为已知. 弹性模量E,线膨胀系数α为已知. ∆ LF 杆内的温度应力 温度应力. 求温度升高 ∆T 时，杆内的温度应力.
A B
FA
A
B
B'
FB
l ∆ LT A
作业：2.47 作业：
平衡方程： 平衡方程：FA=FB ∆L 变形关系： 变形关系： T=|∆LF| B' α 补充方程： 补充方程： L ∆T = FBL/(EA) ∴ FB = EAα∆T σ = Eα∆T 例题：2.12 例题： 练习：2.48 练习：
2.什么是装配应力？ 2.什么是装配应力？ 什么是装配应力 B D C 图示杆系, 图示杆系,若3杆尺寸有微小误差, 杆尺寸有微小误差, 3 2 则在杆系装配好后, 则在杆系装配好后,各杆将处于图 1 α α 中位置,因而产生轴力.3 .3杆的轴力 中位置,因而产生轴力.3杆的轴力 l 为拉力,1.2杆的轴力为压力. ,1.2杆的轴力为压力 为拉力,1.2杆的轴力为压力.这种 A′ 附加的内力就称为装配内力. 附加的内力就称为装配内力.与之 δ 相对应的应力称为装配应力 (initial stresses) . A 平衡方程： 平衡方程：F3 − 2F1 cos α = 0 变形关系： 变形关系：∆L 3 + ∆L1 = δ cos α 补充方程： 补充方程： 作业：2.49 作业：
δ
求解超静定问题 的思路： 的思路：
平衡方程 补充方程
联立求解， 联立求解，得出约 束力或内力
例：在两端固定的杆件的截面C上，沿轴线作用F力， 在两端固定的杆件的截面C 沿轴线作用F 求两端的反力。 求两端的反力。
a
C
b
习题2.40： 习题2.40： 2.40
A
F
B
例：受预拉力10kN拉紧的绳缆，C点再施加15施加15kN的力， 10kN拉紧的绳缆 15kN的力 AC段的内力 段的内力？ 求BC 、AC段的内力？ 点的作用范围？ C点的作用范围？ 习题2.42： 习题2.42： 2.42
B1 C1 A1 2 L 1 B C A a a
FN1
FN3 x
FN2
平衡方程： N1 平衡方程：F = F N2 C1 C' F − 2F = 0 3 N3 N1 N 变形关系： 补充方程： N1 变形关系： L1 + ∆L3 = δ 补充方程： F L + F 3L = δ ∆ E A E3A3 例题：2.13 例题：
例：两刚体用钢杆 1、2连接,杆长L=200mm. 现将制 刚体用钢杆 连接,杆长L=200mm. 造得过长了δ=0.11mm的铜杆 装入CC 的位置。 的铜杆3 造得过长了δ=0.11mm的铜杆3装入CC1的位置。计算 各三根杆内的装配应力. 各三根杆内的装配应力. 已知： =210GPa。 已知：钢杆直径d=10mm, E=210GPa。 铜杆横截面积为20 30mm的矩形 20× 的矩形, 铜杆横截面积为20×30mm的矩形, E3=100GPa.