一信号的定义及分类

第一章主要讲什么是信号，什么是系统。

首先来了解一下信号，我们平时见到的报道称为消息，消息中有意义的内容称为信息，信号是信息的载体，是信息的物理体现。

简而言之，就是通过信号传递信息。

我们平时见到的十字路口的红绿灯就是一种光信号，我们常见的广告牌也可以说成文字、图像信号，电视机接收的信号是一种电信号，而我们主要讨论的就是电信号，简称信号。

电信号的基本形式是随时间变化的电压或电流，通常我们用描述信号，也可以用波形来表示。

需要注意的是在这门课里，“信号”与“函数”两词常相互通用。

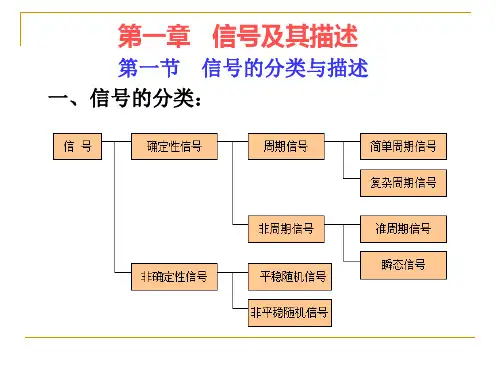
1、信号的分类方法很多，下面是从不同的角度对信号分类：2、按实际用途分类：电视信号，雷达信号，控制信号，通信信号，广播信号3、按所具有的时间特性划分：确定信号和随机信号；连续信号和离散信；周期信号和非周期信号；能量信号与功率信号；因果信号与反因果信号；实信号与复信号等等。

下面从时间角度看一下各种信号的含义：确定信号与随机信号：顾名思义，确定性信号就是信号可以用一个确定的时间函数表示。

有便可推知，而随机信号指信号不能用一个确定的时间函数加以确定，它只能用统计方法进行描述,就像在相同条件下，随机信号不能准确的重现某一数值，只能得到某值得概率。

连续信号和离散信号：连续信号就是在连续时间都有定义的信号，至于值域可连续也可不连续，幅值连续为模拟信号（如图一中），否则为量化信号（如图一中）。

离散时间信号是仅在一些离散的时间才有定义的信号，需要注意的是其余时间无定义（不是0）。

幅值连续是取样信号（如图二），离散是数字信号（如图三）。

图一图二图三如图三的仅在一些离散时刻才有定义，间隔，取等间隔，离散信号：，简写为称为序列，k为序号。

用表达式可表示为：，其他或写为：此处必须标明模拟信号通过抽样可化为抽样信号，抽样信号经过量化可化为数字信号，以后会详细讲述变换过程。

周期信号和非周期信号：可以从字面含义理解。

连续周期信号满足：，离散周期信号满足：，满足上述关系的最小（或整数）称为该信号的周期。

信号与系统考研笔记一、信号与系统的基本概念1.信号的定义和分类：信号可以分为确定性信号和随机信号，周期信号和非周期信号，连续时间信号和离散时间信号等。

2.系统的定义和分类：系统可以分为线性系统和非线性系统，时不变系统和时变系统，连续时间和离散时间系统等。

3.信号的基本运算：包括信号的加法、减法、乘法、除法等基本运算。

4.系统的基本运算：包括系统的串联、并联、反馈等基本运算。

二、傅里叶变换1.傅里叶级数和傅里叶变换的定义：傅里叶级数用于表示周期信号，而傅里叶变换则用于表示非周期信号。

2.傅里叶变换的性质：包括对称性、线性（叠加性）、奇偶虚实性、尺度变换特性、时移特性、频移特性、微分特性、积分特性、卷积特性、相关与自相关特性等。

3.傅里叶变换的应用：包括频域分析、系统响应分析、滤波器设计等。

三、拉普拉斯变换和Z变换1.拉普拉斯变换的定义和性质：拉普拉斯变换是用来分析具有无穷大的时间域信号的一种方法。

2.Z变换的定义和性质：Z变换是用来分析离散时间信号的一种方法。

3.拉普拉斯变换和Z变换的应用：包括系统响应分析、控制系统设计等。

四、线性时不变系统1.LTI系统的定义和性质：LTI系统是指具有线性特性和时不变特性的系统。

2.LTI系统的分析和设计：包括系统的频率响应分析、系统稳定性分析、系统均衡和滤波等。

3.LTI系统的状态空间表示：包括状态空间模型的建立、系统的稳定性和可控性分析等。

五、采样定理和离散傅里叶变换1.采样定理的理解和应用：采样定理规定了采样频率和信号带宽之间的关系，对于连续时间信号的离散化采样具有重要意义。

2.DFT的理解和应用：DFT是离散时间信号的一种基本运算，可以用于信号的分析和处理。

3.快速傅里叶变换（FFT）的理解和应用：FFT是一种高效计算DFT的算法，可以大大提高信号处理的速度和效率。

六、信号与系统的应用和实践1.数字信号处理的应用和实践：包括数字滤波器设计、数字波形合成、数字音频处理等。

信号Signal信号是表示消息的物理量，如电信号可以通过幅度、频率、相位的变化来表示不同的消息。

这种电信号有模拟信号和数字信号两类。

信号是运载消息的工具，是消息的载体。

从广义上讲，它包含光信号、声信号和电信号等。

按照实际用途区分，信号包括电视信号、广播信号、雷达信号，通信信号等；按照所具有的时间特性区分，则有确定性信号和随机性信号等。

信号是运载消息的工具，是消息的载体。

从广义上讲，它包含光信号、声信号和电信号等。

例如，古代人利用点燃烽火台而产生的滚滚狼烟，向远方军队传递敌人入侵的消息，这属于光信号；当我们说话时，声波传递到他人的耳朵，使他人了解我们的意图，这属于声信号；遨游太空的各种无线电波、四通八达的电话网中的电流等，都可以用来向远方表达各种消息，这属电信号。

人们通过对光、声、电信号进行接收，才知道对方要表达的消息。

分类对信号的分类方法很多，信号按数学关系、取值特征、能量功率、处理分析、所具有的时间函数特性、取值是否为实数等，可以分为确定性信号和非确定性信号（又称随机信号）、连续信号和离散信号（即模拟信号和数字信号）、能量信号和功率信号、时域信号和频域信号、时限信号和频限信号、实信号和复信号等。

模拟信号和数字信号：模拟信号是指信号波形模拟着信息的变化而变化，其主要特征是幅度是连续的，可取无限多个值；而在时间上则可连续，也可不连续。

如图2所示。

数字信号是指不仅在时间上是离散的，而且在幅度上也是离散的，只能取有限个数值的信号。

如电报信号，脉冲编码调制(PCM，Pulse Code Modulation)信号等都属于数字信号。

二进制信号就是一种数字信号，它是由“1”和“0”这两位数字的不同的组合来表示不同的信息。

人们依据在通信系统中传送的是模拟信号还是数字信号，把通信系统分成模拟通信系统和数字通信系统。

如果送入传输系统的是模拟信号，则这种通信方式为模拟通信。

如今所使用的大多数电话和广播、电视系统都是采用的模拟通信方式。

信号的分类知识点总结一、信号的基本概念1. 信号的定义信号是带有信息的波形或者电流，可以传送信息的载体。

在通信系统中，信号是指传输中的模拟信号或者数字信号，可以是声音、图像、文本等形式。

在控制系统中，信号指的是传达控制信息或者参数的电气或者物理量。

2. 信号的分类信号可以按照多种特性进行分类，包括：- 按照时间域特性分类：分为连续信号和离散信号。

- 按照频率域特性分类：分为基带信号和载波调制信号。

- 按照数量级分类：分为低频信号、中频信号和高频信号。

- 按照波形形状分类：分为周期信号和非周期信号。

二、信号的时间域特性分类1. 连续信号连续信号指的是在时间上是连续变化的信号，可以用连续的函数来表示。

例如，模拟语音信号、模拟视频信号等都是连续信号。

2. 离散信号离散信号指的是在时间上是不连续的信号，可以用离散的序列来表示。

例如，数字音频信号、数字图像信号等都是离散信号。

三、信号的频率域特性分类1. 基带信号基带信号指的是没有经过频率变换的信号，其频率范围包括直流到最大可用频带之间的所有频率。

例如，普通的模拟声音信号就属于基带信号。

2. 载波调制信号载波调制信号指的是经过频率变换的信号，是将基带信号调制到一个高频信号载波上进行传输的信号。

例如，调幅调制（AM）、调频调制（FM）等都属于载波调制信号。

四、信号的数量级分类1. 低频信号低频信号指的是频率在几百赫兹以下的信号。

例如，语音信号、直流电信号等都属于低频信号。

2. 中频信号中频信号指的是频率在几百赫兹到几百千赫兹之间的信号。

例如，射频信号、调制信号等都属于中频信号。

3. 高频信号高频信号指的是频率在几百千赫兹以上的信号。

例如，微波信号、毫米波信号等都属于高频信号。

五、信号的波形形状分类1. 周期信号周期信号指的是在一定时间间隔内具有重复的波形形状的信号。

例如，正弦信号、方波信号等都是周期信号。

2. 非周期信号非周期信号指的是没有重复的波形形状的信号。

信号与系统基本概念和分类在现代通信领域，信号与系统是一门基础而重要的学科。

理解信号与系统的基本概念和分类对于深入研究通信原理和系统设计至关重要。

本文将介绍信号与系统的基本概念和分类，并探讨其在实际应用中的重要性。

一、信号的基本概念信号是信息的载体，可以通过某种形式或载体传递。

信号的基本概念包括以下几个方面：1. 信号的定义：信号是随时间变化的物理量。

它可以是连续的、离散的、周期的或非周期的。

2. 信号的特征：信号可以通过其振幅、频率、相位、时间等特征进行描述。

这些特征可以在频域或时域中进行观察和分析。

3. 信号的分类：信号可以分为连续信号和离散信号。

连续信号在时间和幅度上都是连续变化的，例如声音信号、电压信号等；离散信号在时间和幅度上都是离散变化的，例如数字信号、脉冲信号等。

二、系统的基本概念系统是对信号进行处理或传输的过程或设备。

理解系统的基本概念可以帮助我们分析和设计复杂的通信系统。

以下是系统的基本概念：1. 系统的定义：系统是由一组有序的组件或部件构成，它们相互作用或协作以实现特定的功能。

2. 系统的输入与输出：系统接受输入信号，并根据某种规则对其进行处理，产生输出信号。

3. 系统的状态：系统的状态是系统在某一时刻的描述，可以用于描述系统的性能和行为。

三、信号与系统的分类信号与系统可以根据不同的特征进行分类。

以下是几种常见的分类方式：1. 按信号的数学表示方式分类：a. 连续时间信号：用函数描述，例如正弦信号、指数信号等。

b. 离散时间信号：用序列描述，例如单位样本序列、冲激序列等。

2. 按系统的输入输出关系分类：a. 线性系统：输出与输入之间存在线性关系，满足叠加原理。

b. 非线性系统：输出与输入之间不存在线性关系，不满足叠加原理。

3. 按系统的时变性分类：a. 时不变系统：系统的性质不随时间改变。

b. 时变系统：系统的性质随时间改变。

四、信号与系统的应用信号与系统的理论和方法在现代通信领域有着广泛的应用。

考研《信号与系统》考研重点考点归纳第1章信号与系统1.1考点归纳一、信号的描述及分类1．信号的定义信号是指消息的表现形式与传送载体。

2．信号的分类及特性（1）确定信号与随机信号确定信号：由确定系统产生、具有确定参数、按确定方式变化的信号。

随机信号：具有不可预知的不确定性信号。

实际中的信号绝大部分都是随机信号。

（2）连续信号与离散信号连续信号：在定义的时间区域内任意时间点上都有定义的信号。

离散信号：只在某些不连续时间值上给定函数值的信号。

（3）周期信号与非周期信号周期信号：=，n∈Z非周期信号：≠，n∈Z（4）奇信号与偶信号偶信号：或。

奇信号：或。

任何信号=一个偶信号＋一个奇信号，其中偶部和奇部分别为：（5）功率信号与能量信号功率信号：信号平均功率为非零的有限值。

能量信号：信号总能量为非零的有限值。

3．信号的能量与功率表1-1 能量与功率计算公式说明：（1）总能量有限的信号，平均功率为零；（2）平均功率有限的信号，能量无穷大。

二、信号的运算1．信号的相加与相乘同一时刻两信号之值对应相加减乘：或2．信号的延时信号延时后的信号：式中，＞0，波形在保持信号形状不变的同时，右移的距离；＜0则向左移动。

3．信号的反褶与尺度变换（1）信号的反褶形式：，波形对称于纵坐标轴的反褶。

（2）信号的尺度变换形式：，有以下规则：①，波形为的波形在时间轴上压缩为原来的；②，波形为的波形在时间轴上扩展为原来的。

③，波形为的波形反转并压缩或展宽至。

4．形如的波形变换（1）先向右（左）平移b个单位，再在此基础上压缩或扩展原来的；（2）先压缩或扩展原来的，再向右（左）平移个单位。

三、指数信号与正弦信号1．连续时间复指数信号与正弦信号连续时间复指数信号具有如下形式：其中C和α一般为复数。

（1）实指数信号实指数信号：C和α都是实数的x（t）。

α的正负对波形的影响：①若α是正实数，x（t）随t的增加而呈指数增长；②若α是负实数，x（t）随t的增加而呈指数衰减。

第一章主要讲什么是信号，什么是系统。

首先来了解一下信号，我们平时见到的报道称为消息，消息中有意义的内容称为信息，信号是信息的载体，是信息的物理体现。

简而言之，就是通过信号传递信息。

我们平时见到的十字路口的红绿灯就是一种光信号，我们常见的广告牌也可以说成文字、图像信号，电视机接收的信号是一种电信号，而我们主要讨论的就是电信号，简称信号。

电信号的基本形式是随时间变化的电压或电流，通常我们用描述信号，也可以用波形来表示。

需要注意的是在这门课里，“信号”与“函数”两词常相互通用。

1、信号的分类方法很多，下面是从不同的角度对信号分类：2、按实际用途分类：电视信号，雷达信号，控制信号，通信信号，广播信号3、按所具有的时间特性划分：确定信号和随机信号；连续信号和离散信；周期信号和非周期信号；能量信号与功率信号；因果信号与反因果信号；实信号与复信号等等。

下面从时间角度看一下各种信号的含义：确定信号与随机信号：顾名思义，确定性信号就是信号可以用一个确定的时间函数表示。

有便可推知，而随机信号指信号不能用一个确定的时间函数加以确定，它只能用统计方法进行描述,就像在相同条件下，随机信号不能准确的重现某一数值，只能得到某值得概率。

连续信号和离散信号：连续信号就是在连续时间都有定义的信号，至于值域可连续也可不连续，幅值连续为模拟信号（如图一中），否则为量化信号（如图一中）。

离散时间信号是仅在一些离散的时间才有定义的信号，需要注意的是其余时间无定义（不是0）。

幅值连续是取样信号（如图二），离散是数字信号（如图三）。

图一图二图三如图三的仅在一些离散时刻才有定义，间隔，取等间隔，离散信号：，简写为称为序列，k为序号。

用表达式可表示为：，其他或写为：此处必须标明模拟信号通过抽样可化为抽样信号，抽样信号经过量化可化为数字信号，以后会详细讲述变换过程。

周期信号和非周期信号：可以从字面含义理解。

连续周期信号满足：，离散周期信号满足：，满足上述关系的最小（或整数）称为该信号的周期。

信号重要基础知识点信号是一种用于传递信息或者在系统中进行通信的方法。

在现代科技和通信领域中，信号是非常重要的基础知识点。

下面将介绍几个与信号相关的重要基础知识点。

1. 信号的定义和分类：信号可以被定义为随时间、空间或其他变量的变化而变化的某种物理量。

根据其物理参数，信号可以被分类为模拟信号和数字信号。

模拟信号是连续时间和连续幅度变化的信号，而数字信号是离散时间和离散幅度变化的信号。

2. 信号的特征和表示：信号可以通过其幅度、频率、相位和时间特性进行描述。

幅度表示信号的振幅或强度，频率表示信号的周期性，相位表示信号相对于某个参考点的偏移，而时间特性表示信号的时域行为。

信号可以用数学方程、图形或者频谱表示进行分析和处理。

3. 傅里叶分析和频谱：傅里叶分析是一种将信号分解成一系列基本频率组成的方法，而频谱则表示信号在频域中不同频率成分的强度或能量分布。

傅里叶变换是用于从时域到频域的转换，而逆傅里叶变换则是将频域信号恢复到时域。

4. 信号传输和衰减：在信号传输过程中，信号可能会受到衰减和失真的影响。

衰减是信号幅度随着传输距离增加而减小的过程，而失真则是信号形状或频谱发生变化的过程。

为了克服这些问题，通信系统通常会采用调制、编码和纠错等技术来提高信号的传输质量。

5. 抽样和量化：数字信号的表示需要进行抽样和量化。

抽样是将连续时间的模拟信号转换为离散时间的数字信号，而量化则是将连续幅度的模拟信号转换为离散幅度的数字信号。

合适的抽样率和量化精度对于保证数字信号的准确性和保真度至关重要。

这些是关于信号重要的基础知识点。

了解信号的定义、分类、特征和表示方法，以及信号传输过程中可能遇到的问题和解决方案，将有助于深入理解信号处理、通信系统以及其他相关领域的知识。

信号与系统第一章总结1、信号的分类（1）周期信号和非周期信号两个周期信号x(t)，y(t)的周期分别为T 1和T 2，若其周期之比T 1/T 2为有理数，则其和信号x(t)+y(t)仍然是周期信号，其周期为T 1和T 2的最小公倍数。

（2）连续信号和离散信号连续时间信号：信号存在的时间范围内，任意时刻都有定义。

用t 表示连续时间变量。

离散时间信号：在时间上是离散的，只在某些不连续的规定瞬时给出函数值， 用n 表示。

（3）模拟信号，抽样信号，数字信号 模拟信号：时间和幅值均为连续的信号。

抽样信号：时间离散，幅值连续的信号。

数字信号：时间和幅值均为离散的信号。

（4）按照信号能量特点分类：能量受限信号：若信号f (t)的能量有界，即E<∞ ,则称其为能量有限信号，简称能量信号，此时P = 0。

功率受限信号：若信号f(t)的功率有界，即P<∞ ,则称为功率有限信号，简称功率信号，此时E = ∞。

PS ：时限信号为能量信号；周期信号属于功率信号。

2、典型的确定性信号（1）指数信号： ， α=0 直流（常数）；α<0 指数衰减；α>0指数增长。

通常把称为指数信号的时间常数，记作τ ,代表信号衰减速度，具有时间的量纲。

对时间的微分和积分仍然是指数形式（2）正弦信号：，振幅K ，周期T=ωπ2 ,初相衰减正弦信号：对时间的微分和积分仍然是同频率的正弦信号 （3）复指数信号：α1θdt t f E 2)(⎰∞∞-∆=⎰-∞→=222|)(|1lim T T T dt t f T P t K t f αe )(=)sin()(θω+=t K t f ()0sin e )(>⎩⎨⎧<≥=-αωαt t t K t f t()()t K t K t K t f t t stωωσσsin e j cos e )( e )(+=∞<<-∞=为复数，称为复频率j ωσ+=s rad/s的量纲为 ，/s 1 的量纲为 ωσ振荡衰减增幅等幅⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≠<≠>≠= 0 ,0 0 ,0 0 ,0ωσωσωσ⎪⎩⎪⎨⎧=<=>==衰减指数信号升指数信号直流 0 ,0 0 ,0 0 ,0ωσωσωσ（4）抽样信号（重点）： 性质：1. 偶函数2. 3. 4.5. 6.（5）钟形信号（高斯函数）：3、信号的平移，反褶，展缩（1）平移：左加右减（注意符号）（2）反褶：关于y 轴对称（3）展缩：f(t)到f(at)，图形变换(1/a)倍变换方法： 1. 先展缩：a>1，压缩a 倍； a<1，扩展1/a 倍 2. 后平移：+，左移b/a 单位；－，右移b/a 单位 3. 加上倒置：4、阶跃信号和冲激信号（1）单位阶跃信号（通常以u （t ）表示）门函数：符号函数：ttt sin )Sa(=)Sa(lim ，即1)Sa(,00===→t t t t 3,2,1π,0)Sa(=±==n n t t ，⎰⎰∞∞-∞==πd sin ,2πd sin 0t t t t t t 0)Sa(lim=±∞→t t ()()t t t ππsin )sinc(=2e )(⎪⎭⎫ ⎝⎛-=τt E tf ()()()[]()0 >±=±→a a b t a f b at f t f 设()()[]a b t a f b at f -=±-()[(/)]f t f a t b a →±()()f t f at →210 0100)(点无定义或⎩⎨⎧><=t t t u ()⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛+=22ττt u t u t f ⎩⎨⎧<->=0101)sgn(t t t（2）单位冲激信号：①定义：狄拉克函数 只在t=0时，函数值不为0；积分面积为1；t =0 时，为无界函数。

实验一练习一信号的特性及其频谱分分析实验原理一. 信号的概念和分类1. 信号在通信与信息系统中，传输的主体是信号，系统所包含的各种电路、设备都是为了实施这种传输。

因此，电路系统设计和制造的要求，必然要取决于信号的特性。

随着待传输信号的日益复杂，相应地，信号传输系统中的元器件、电路的结构等也日益复杂。

因此，对信号进行分析变得越来越重要。

2. 信号的分类下面从不同角度对信号进行分类。

确定信号和随机信号：若其在任何时间的值都是确定已知的，那么是确定信号；若信号在实际发生之前具有一定的不确定性，则表明信号是随机信号。

连续信号和离散信号：将一个信号表示成为时间t的函数，如果其时间变量t的取值是连续的，那么这个信号就称为连续信号。

若信号只在某些不连续的时间点上有确定的取值，则称信号是离散信号。

模拟信号和数字信号：时间或幅度连续的信号称为模拟信号，时间和幅度都离散的信号称为数字信号。

周期信号和非周期信号：在一个可以测量的时间范围内完成一种模式，并且在后续的相同时间范围内重复这一模式，这种信号是周期信号；不随时间变化出现重复的模式或循环，则是非周期信号。

二. 周期模拟信号周期模拟信号可以分为简单类型或复合类型两种。

简单类型模拟信号，即正弦波，不能再分解为更简单的信号。

而复合型模拟信号则是由多个正弦波信号组成的。

正弦波是周期模拟信号的最基本形式。

可以看做一条简单的震荡曲线，在一个周期内的变化是平滑、一直的、连续的、起伏的曲线。

下图就是一个正弦波，每个循环由时间轴上方的单弧和后跟着的时间轴下方的单弧构成。

图1-1-1 正弦波单个正弦波可以用三个参数表示：峰值振幅、频率和相位。

这三个参数完全决定正弦波。

1. 峰值振幅信号的峰值振幅是其最高强度的绝对值，与其携带的能量成正比。

图1-1-2表示了两个信号和它们的峰值振幅。

图1-1-2 相位和频率相同但振幅不同的两个信号2. 周期和频率周期是信号完成一个循环所需要的时间，以秒为单位。