苏教版高中数学必修一第课时——二次函数与一元二次方程

二次函数和方程课型：新授一、学习目标：1、使学生能熟练地画出二次函数y=ax2+bx+c(a≠0)的图象，并能结合图象初步能判断a、b、c的符号。

2、结合二次函数y=ax2+bx+c(a≠0)的图象感受二次函数与不等式、方程的关系。

二、〔一〕复习旧知：1、二次函数y=ax2+bx+c(a≠0)的对称轴是_______，顶点坐标是___________。

2、无论x取任何实数，函数y=x2+2x-3中，函数值y的取值范围是〔〕A、y≥-4B、y≤-4C、y≥-3D、取任何实数3、当0≤x≤5时，函数y=3x2-12x+5的取值范围是________________4、在右图中：〔1〕当x满足_________时，y=0 〔2〕当x满足_________时，y＞0〔3〕当x满足_________时，y＜0〔二〕自主探究问题1：想一想，如何根据图象确定二次函数y=ax2+bx+c(a≠0)中a、b、c的符号，〔1〕a的符号与抛物线的___________有关，有什么结论？______________________________________〔2〕抛物线y=ax2+bx+c(a≠0)与y轴的交点坐标是________因此抛物线与y轴的交点:①在y轴正半轴上时，c与0的大小关系是___________；②在y轴负半轴上时，c与0的大小关系是___________；③在原点时，c与0的大小关系是___________。

〔3〕对称轴与_____ 有关，如何确定b的符号?〔4〕二次函数y=ax2+bx+c(a≠0)的图象如下图，那么〔〕A、a＜0，b＞0，c＜0B、a＜0，b＜0，c＞0，C、a＜0，b＜0，c＜0，D、a＜0，b＞0，c＞0三、例1、〔1〕二次函数y=ax2+bx+c(a≠0)的图象如下图，那么你能判断出以下量的符号吗？a___0;b___0;c____0;abc___0、2a+b___0、a+b+c___0、a-b+c___0、b2-4ac___0 、4a+2b+c____0。

2.5.1 二次函数与一元二次方程(1)教学目标：1.让学生熟练掌握二次函数的图象，并会判断一元二次方程根的存在性及根的个数2.让学生了解函数的零点与方程根的联系3.让学生认识到函数的图象及基本性质（特别是单调性）在确定函数零点中的作用 4．培养学生动手操作的能力教学重点：确定方程实数根的个数教学难点：通过计算器或计算机做出函数的图象 教学过程： 引入问题 问题1.一元二次方程20(0)ax bx c a ++=≠的实根与二次函数2(0)y ax bx c a =++≠的图象有什么关系？通过复习二者之间的关系引出新课（板书课题）：一元二次方程20(0)ax bx c a ++=≠的实数根也称为函数2(0)y ax bx c a =++≠的零点.1．函数零点的定义：对于函数()y f x =，我们把使()0f x =的实数x 叫做函数()y f x =的零点.这样，函数()y f x =的零点就是方程()0f x =的实数根，也就是函数()y f x =的图象与x 轴的交点的横坐标. 2．零点的一般结论方程()0f x =有实数根函数()y f x =的图象与x 轴有交点函数()y f x =有零点问题2.如何判断一元二次方程的零点的个数?对二次函数图象中零点的观察可得如下性质.零点个数 2个 2个相等的零点 0个练习: (课时训练P59例2)求实数k 的取值范围,使关于x 的方程1x k x+=有两个不相等的实根.解法一: (数形结合法) 阅读课时训练P20页,利用函数1y x x=+的图象求解.解法二: (判别式法)原方程可化为210x kx -+=,由题意可得240k ∆=->,∴2k >或2k <-.∴2k >或2k <-时, 方程1x k x+=有两个不相等的实根.3．零点的性质对于任意函数()y f x =，只要它的图象是连续不间断的，则有 （1）当它通过零点时（不是二重零点），函数值变号．如函数2()23f x x x =--的图象在零点1-的左边时，函数值取正号，当它通过第一个零点1-时，函数值由正变为负，再通过第二个零点3时，函数值又由负变成正． （2）在相邻两个零点之间所有的函数值保持同号．4．注意点（1）函数是否有零点是针对方程是否有实数根而言的，若方程没有实数根，则函数没有零点．（2）如方程有二重实数根，可以称函数有二阶零点．阅读课本P75页例2例2的结论:由例2的结论可推广得下面的定理5．勘根定理 (介值定理) (根的存在性定理) 如果函数()y f x =在区间[,]a b 上的图象是连续不间断的一条曲线，并且有()()0f a f b ⋅<那么函数()y f x =在区间(,)a b 内有零点，即存在(,)c a b ∈，使得()0f c =，这个c 也就是方程()0f x =的实数根．题型1.零点的判断 例1．函数2()ln f x x x=-的零点所在的大致区间是（ ） A ．（1，2） B ．（2，3） C ．1(1,)e和（3，4） D ．(,)e +∞分析：从已知的区间(,)a b ，求()f a 和()f b ，判断是否有()()0f a f b ⋅<. 解析：因为(1)20,(2)ln 210f f =-<=-<， 故在（1，2）内没有零点，非A. 又2(3)ln 303f =->，所以(2)(3)0f f ⋅<， 所以()f x 在（2，3）内有一个零点，选B.例2．若方程2210ax x --=在（0，1）内恰有一解，求实数a 的取值范围． 分析：令2()21f x ax x =--在（0，1）内恰有一解，则(0)(1)0f f ⋅<，解出a ． 解析：令2()21f x ax x =--，因为方程在（0，1）内恰有一解， 所以(0)(1)0f f ⋅<，即1(22)0a -⋅-<，解得1a >.练习: (课本P74例1)分析: 证法一,利用0∆>,证明得方程有两个不相等的实数根.证法二,利用二次函数的图象特征: 其开口向上(a >) 且(0)0f <则函数的图象必与x 轴有两个不同的交点.()0af m < 还有其它证法吗?提示:可以求最小值小于0. 还有配方法!问题3.如果二次开口向下呢?如何证明方程仍有两个不同的实数根? 一定要用(0)f 才行吗?你能分类说出二次函数有两个实数根,证法二的一般规律吗?结论: 二次函数2() (0)f x ax bx c a =++≠, 若满足0,0,()0,()0.a a f m f m ><⎧⎧⎨⎨<>⎩⎩或,则方程20 (0)ax bx c a ++=≠必有两个不相等的实数根.即:题型2.零点的个数计算例3．求函数()ln 26f x x x =+-的零点个数.分析：求函数的零点个数实际上是判断方程有没有实数根，有几个实数根的方法，其步骤是：（1）利用计算器或计算机作,()x f x 的对应值表； （2）作出函数()y f x =的图象； （3）确定()y f x =的单调性；（4）若在区间[,]a b 上连续，并且有()()0f a f b ⋅<，那么函数()y f x =在区间(,)a b 内有一个实数根；（5）结合单调性确定其定义域内零点个数，即实数根个数． 结合计算机利用几何画板作出函数的图象观察．分析: 可以判断其为(0,)+∞上的增函数∵(2)(ln 22)0,(3)ln30f f =-<=>, ∴(2)(3)0f f <∴在(2,3)区间上有一个实数根,且该零点有且仅有一个.例4．二次函数2(0)y ax bx c a =++≠中，0a c ⋅<，则函数的零点个数是( )A ．1个B ．2个C ．0个D ．无法确定分析：分析条件0a c ⋅<，a 是二次项系数，确定抛物线的开口方向，(0)c f =，所以(0)0a c a f ⋅=⋅<，由此得解．解：因为(0)c f =，所以(0)0a c a f ⋅=⋅<，即a 与(0)f 异号，即0(0)0a f >⎧⎨<⎩或(0)0a f <⎧⎨>⎩ 所以函数必有两个零点，故选B.题型3.二次函数的图象上其它特征点的信息捕捉 练习: (课时训练P59例1 练习1)二次函数2y ax bx c=++则点(,)cP a b在 ( )A. 第一象限B.第二象限C.第三象限D.第四象限解析:开口向下可得0a <, 令0x =可得0c >,对称轴在x 轴右方可得02ba->, 即得0b >.∴0,0c a b <>,即点(,cP a b在第二象限, 应选B.小结: 二次函数的系数的符号与三个条件有关:①开口方向(a ) ; ②与y 轴的交点 (c ) ; ③对称轴在y 的哪侧 (2ba-) .试一试: 应用此法可立即解得课堂练习1 2 的答案为? D D例4. (课时训练P59练习3)如图,抛物线2(0)y ax bx c a =++≠经过点(-1,0) .(1)试确定a b c ++的符号;(2)求证:方程20ax bx c ++=的另一根0x 满足0(3)求证: 0b a << .解析:(1)如图知,(1)0f a b c =++>. (2)由图象知,(0)0f <, 又∵(1)0f >, ∴()f x 的另一个零点在区间(0,1)上.即方程20ax bx c ++=的另一根0x 满足001x <<; (3)∵图象开口向上, ∴0a >.又∵(1)0f -=, ∴0a b c -+=.而0c <, ∴0a b c -=->, 即a b >.∵(1)0f a b c =++>, 0a b c -+= ,∴()20a b c a b c b ++--+=>, 即得0b >. ∴0b a << .作业布置: 课时训练.。

高一数学二次函数与一元二次方程教案高邮市送桥中学知识目标:（1）会用判别式的符号解释二次函数图象与x 轴交点及一元二次方程的根。

（2）理解解函数的零点与方程根的联系及判断函数的零点所在的大致区间。

能力目标：体验并理解函数与方程相互转化的数学思想培和数形结合的数学思想。

情感目标：培养学生积极探索，主动参与，大胆创新，勇于开拓的精神 教学过程: 一、引入等式20ax bx c ++=()0a ≠是关于x 的一元二次方程，关系式2y ax bx c =++()0a ≠则是关于自变量x 的二次函数。

今天我们将进一步研究它们之间的关系。

二、新授 观察思考：1、 几个具体的一元二次方程及其对应的二次函数，如①方程2230x x --=与函数223y x x =--；②方程2210x x -+=与函数221y x x =-+； ③方程2230x x -+=与函数223y x x =-+。

研讨探究问题：一元二次方程的根与二次函数图象和x 轴交点坐标有什么关系 ？ 探究点一：二次函数图象与一元二次方程根的关系。

⑴以①为例（幻灯片）结论：一元二次方程2230x x --=的判别式∆＞0 ⇔一元二次方程2230x x --=有两个不相等的实数根⇔对应的二次函数223y x x =--的图象与x 轴有两个交点为（3，0），（–1，0）。

（2）再研究②③，能得类似的结论吗？结论：一元二次方程2210x x -+=判别式∆=0一元二次方程2210x x -+=⇔有两等根⇔对应的二次函数221y x x =-+的图象与x 轴有唯一的交点为（1，0）。

一元二次方程判别式2230x x -+=∆﹤0 ⇔一元二次方程2230x x -+= 方程无实数根⇔对应的二次函数223y x x =-+的图象与x 轴没有交点。

联想发散2、一元二次方程20a x b x c ++=（a ＞0）根的个数及其判别式与二次函数2y a x b x c =++（a ＞0）图象与x 轴的位置之间有什么联系？）以a ＞0为例,如下表所示:思考：当二次函数2y ax bx c =++（a ﹤0）时，是否也有类似的结论呢？ 探究点二：函数的零点一元二次方程20ax bx c ++=()0a ≠的的实数根就是二次函数c bx ax y ++=2的值为零时自变量的x 的值，也就是二次函数2y ax bx c =++的图象与x 轴交点的横坐标，因此一元二次方程20ax bx c ++=()0a ≠的的实数根也称为二次函数2y ax bx c =++()0a ≠的零点。

§2.5.1 二次函数与一元二次方程(2)教学目标：1.让学生熟练掌握二次函数的图象，并会判断一元二次方程实根的分布情况2.能够通过图象分析法,求一元二次方程实数分布中字母参数的取值范围.3. 培养分类讨论、转化的能力，综合分析、解决问题的能力；4. 激发学习数学的热情，培养勇于探索的精神，勇于创新精神. 教学重点：一元二次方程的实根分布. 用韦达定理解“含参二次方程的实根分布”问题的基本方法.教学难点：通过问题情境的分析,明确一般要考虑哪些因素以及如何使所列出的代数关系式与图象提供的信息是等价的. 教学过程：引入问题(课时训练P61练习1) (课时训练P51练习3)当||1x ≤时, 函数21y ax a =++的值有正也有负,则实数a 的取值范围是( )A.13a ≥- B.1a ≤- C.113a -<<- D.113a -≤≤-分析:“值有正也有负”是什么意思? 说明该函数的图象有什么样的特征?突破1: 该函数的图象与x 轴必有一个交点且非两个端点1±. 突破2: 该函数图象是一条线段,其两个端点的函数值必一正一负! 解析: 设()21f x ax a =++, 则由已知条件可得(1)0,10,11(1)0,310,3f a a f a ->+>⎧⎧⇒⇒-<<-⎨⎨<+<⎩⎩ 或(1)0,10,(1)0,310,f a f a -<+<⎧⎧⇒⎨⎨>+>⎩⎩此不等式组无解.(舍去) 故应选C.问题1.一次函数的实根是可由特征点的函数值确定,二次函数呢?方程的根的求解问题,需要构建一个与之相应的函数去进行研究,这体现了方程与函数之间的一种必然的联系!实根分布的题型:例1.(1)方程x 2－2ax ＋4＝0的两根均大于1，则实数a 的范围是____________． (2)方程x 2－2ax ＋4＝0的一根大于1 ,一根小于1 ，则实数a 的范围是________． (3)方程x 2－2ax ＋4＝0的一根在(0,1)内, 另一个根在(6,8)内，则实数a 的范围是________．解析：(1)方法一：利用韦达定理，设方程x 2－2ax ＋4＝0的两根为x 1、x 2，则⎪⎩⎪⎨⎧≥∆．，＞－＋－，＞－－00)1()1(0)1)(1(2121x x x x 解之得2≤a ＜25．方法二：利用二次函数图象的特征， 设f （x ）＝x 2－2ax ＋4，则⎪⎩⎪⎨⎧≥∆．＞，＞，10)1(0a f 解之得2≤a ＜25．(2) 方法一：利用韦达定理，设方程x 2－2ax ＋4＝0的两根为x 1、x 2，则12(1)(1)00x x ⎧⎨∆>⎩－－<，．解之得a >25．方法二：利用二次函数图象的特征，设f （x ）＝x 2－2ax ＋4，则(1)0f <解之得a >25．(3) 利用二次函数图象的特征， 设f （x ）＝x 2－2ax ＋4，则(0)0(1)0,(6)0(8)0.f f f f >⎧⎪<⎪⎨<⎪⎪>⎩， 解之得101734a << .反思领悟: 判断二次函数的零点分布的关键在于作出二次函数的图象的草图 , 根据草图列出不等式组, 要注意二次函数的对称轴与△的同时存在性问题.练习:(1)方程ax2－2x＋4＝0的两根均大于1，则实数a的范围是_______．(2)方程ax2－2x＋4＝0的一根大于1 ,一根小于1 ，则实数a的范围是_______．(3)方程ax2－2x＋4＝0的一根在(-1,0)内, 另一个根在(0,1)内，则实数a的范围是____．答案:(1)设f（x）＝ax2－2x＋4，则(1)0,11,0.afa>⎧⎪>⎪⎪⎨>⎪⎪∆≥⎪⎩，或(1)0,11,0.afa<⎧⎪<⎪⎪⎨>⎪⎪∆≥⎪⎩，解之得14a<≤;(2)设f（x）＝ax2－2x＋4，则(1)0.af>⎧⎨<⎩，或(1)0.af<⎧⎨>⎩，解之得20a-<<;(3)设f（x）＝ax2－2x＋4，则0,(1)0(0)0,(1)0.afff>⎧⎪->⎪⎨<⎪⎪>⎩，或0,(1)0(0)0,(1)0.afff<⎧⎪-<⎪⎨>⎪⎪<⎩，解之得2a<-.小结:设二次方程ax2－bx＋c =0 (a≠0), 对应的二次函数 f (x)＝ax2－bx＋c(a≠0)①若方程两个根都大于m,则0,()0,20.af mbma>⎧⎪>⎪⎪⎨<-⎪⎪∆≥⎪⎩，或0,()0,20.af mbma<⎧⎪<⎪⎪⎨<-⎪⎪∆≥⎪⎩，;2a2a②若方程一个根大于m ,另一个根小于m ,则0,()0.a f m >⎧⎨<⎩或0,()0()0.a a f m f m <⎧⇔⋅<⎨>⎩.③若方程有两个实根,一个在(,)a b , 另一个在(,)m n 内, 且b m <, 则0,()0()0,()0,()0.a f a f n f b f m >⎧⎪>⎪⎪>⎨⎪<⎪<⎪⎩，或0,()0()0,()0,()0.a f a f n f b f a <⎧⎪<⎪⎪<⎨⎪>⎪>⎪⎩，2a2a2a2a④若方程有两个实根在(,)m n 内, 则0,()0()0,,20.a f m f n b m n a ⎧⎪>⎪>⎪⎪>⎨⎪⎪<-<⎪⎪∆≥⎩，或0,()0()0,,20.a f m f nb m n a ⎧⎪<⎪<⎪⎪<⎨⎪⎪<-<⎪⎪∆≥⎩，练习1.(课时训练P61例2)当k 为何值时,关于x 的一元二次方程2230kx kx k ++-=的两个根都是负数?提示: ①若方程两个根都大于m ,则0,()0,20.a f m b m a >⎧⎪>⎪⎪⎨<-⎪⎪∆≥⎪⎩，或0,()0,20.a f mb m a <⎧⎪<⎪⎪⎨<-⎪⎪∆≥⎪⎩， ;解析: 设2()23f x kx kx k =++- ,由题意可得, 20,(0)020,244(3)0.k f k k k k k >⎧⎪>⎪⎪-⎨<-⎪⋅⎪∆=--≥⎪⎩，或20,(0)020,244(3)0.k f k k k k k <⎧⎪<⎪⎪-⎨<-⎪⋅⎪∆=--≥⎪⎩， 解之得3k > .2.(课时训练P61例3) 已知关于x 的方程2(2)210xm x m +-+-=有两个不等的实根,且较小的根1x 在区间(0,1)内,求m 的取值范围.分析: ③若方程有两个实根,一个在(,)a b , 另一个在(,)m n 内(,)a b , 则0,()0()0,()0,()0.a f a f n f b f m >⎧⎪>⎪⎪>⎨⎪<⎪<⎪⎩，或0,()0()0,()0,()0.a f a f n f b f a <⎧⎪<⎪⎪<⎨⎪>⎪>⎪⎩，解析:令2()(2)21f x x m x m =+-+- , 由题意可得函数()f x 较小的零点0(0,1)x ∈, ∴(0)0,(1)0.f f >⎧⎨<⎩ ∴210,1(2)210.m m m ->⎧⎨+-+-<⎩∴1,22.3m m ⎧>⎪⎪⎨⎪<⎪⎩∴1223m <<.3.( 课时训练P61练习2 P61练习5)设关于x 的方程22430kx x k --=的两个实根一个小于1,另一个大于1,则实数的取值范围是( )A. 0k >B. 1k >C. 4k <-D. 4k <-或0k >分析: ②若方程一个根大于m ,另一个根小于m ,则0,()0.a f m >⎧⎨<⎩或0,()0()0.a a f m f m <⎧⇔⋅<⎨>⎩.解析: 令2()243f x kx x k =-- 由题意可得20,20,(1)0,(1)0.k k f f ><⎧⎧⎨⎨<>⎩⎩或 即20,20,40,40.k k k k ><⎧⎧⎨⎨--<-->⎩⎩或 解之得40k k <->或.故选D.开放探究题型:例2.已知()()()2f x x a x b =--- (a b <) ,并且,αβ是方程()0f x =的两个根(αβ<),则实数,,a b ,αβ的大小关系可能是( )A. a b αβ<<<B.a b αβ<<<C.a b αβ<<<D.a b αβ<<< 解析设()()()g x x a x b =--, 则()()2f x g x =-, 分别作出此两个函数的图象,如右图所示, 可得a b αβ<<<,故应选A.例3.设函数lg |2|,2,()1, 2,x x f x x -≠⎧=⎨=⎩若关于x 的方程2()()0f x bf x c ++=恰有4个不同的实数解1234,,,x x x x ,则1234()f x x x x +++等于( ) A. 0 B. lg 2 C. lg 4 D. lg 6 解析:由右图可得,当()1f x =时,方程仅有三个不同的 实数解不合题意.由方程有四个不同的实数解可得方程20t bt c ++=有两个不同的实数根12,t t ,且12,1t t ≠.令141232()(),()()f x f x t f x f x t ====, 则14234x x x x +=+=, ∴1423()(8)lg6f x x x x f +++==.故应选D.。

x一、复习引入问题1、不解方程如何判断一元二次方)0(02≠=++a c bx ax 程解的情况。

问题2、画出二次函数322--=x x y 的图象，观察图象，指出x 取哪些值时，0=y 。

二、建构数学1、探究函数)0(2≠++=a c bx ax y 与方程)0(02≠=++a c bx ax 图象之间的关系，填2、零点：对于函数)(x f y =，我们把使0)(=x f 的实数x 叫做)(x f y =的零点； 0)(=x f 有实数根⇔)(x f y =的图象与x 轴有交点⇔)(x f y =有零点。

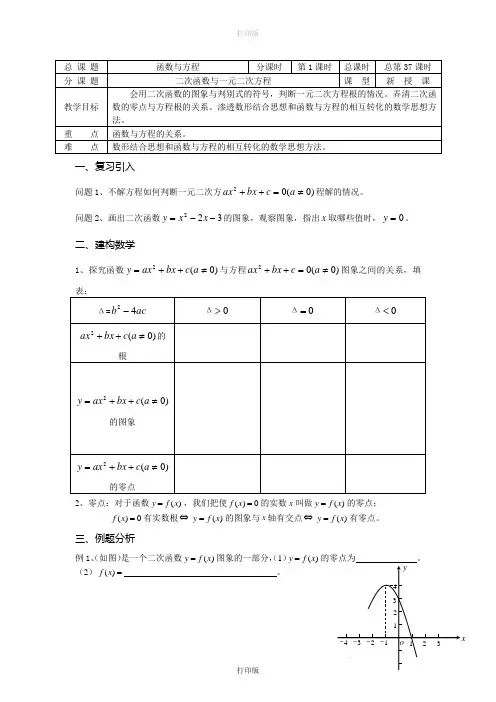
三、例题分析例1、（如图）是一个二次函数)(x f y =图象的一部分，（1）)(x f y =的零点为 。

（2）=)(x f 。

例2、求证：一元二次方程07322=--x x 有两个不相等的实数根（用两种方法证）。

例3、（1）12)(-=x x f 在区间)1,0(上是否存在零点？（2）732)(2-+=x x x f 在区间)2,3(--、)2,1(上是否存在零点？观察：)1()0(f f 值的符号特点；)2()3(--f f 、)2()1(f f 值的符号特点。

结论：如果函数)(x f y =在区间],[b a 上的图象是连续不断的一条曲线，并且0)()(<b f a f ，那么函数)(x f y =在区间),(b a 内有零点。

（即存在),(b a c ∈，使得0)(=c f ．这个c 也就是方程0)(=x f 的根。

）思考：（1）若)(x f y =在],[b a 上是单调函数，且0)()(<b f a f ，则)(x f y =在],[b a 上的零点情况如何？（2）若0x 是二次函数)(x f y =的零点，且n x m <<0，那么0)()(<n f m f 一定成立吗？四、随堂练习1、分别指出下列各图象对应的二次函数)0(2≠++=a c bx ax y 中,,,a b c ∆与0的大小关（1）a ______0，b _____0，c ______0，∆______0（2）a ______0，b _____0，c ______0，2、判断函数12)(2--=x x x f 在区间)3,2(上是否存在零点。