课内试验项目操作分析单
班级________姓名_______学号_______ 编制部门：编制人：编制日期：
项目编号项目名称基尔霍夫定律训练对象
课程名称电工电子技术教材《电工技术》《电子技术基础》学时１
试验目的（１）掌握万用表测量电流、电压的方法及稳压电源的使用方法
（２）掌握基尔霍夫定律的内容和其在电路分析中的应用
（３）培养学生严谨细致，认真负责的工作作风
一、仪器设备：
ZH-12通用电学实验台、万用表
二、注意事项：
1、试验之前应先检查设备、器材的好坏。
2、电路连接时，要注意电源极性，避免反接。
3、使用万用表时，要正确选择档位，且要规范操作。
若选用电压表和电流表则应注意选
用合适量程的表，并且电路连接时要注意极性。
4、测量电压时，应将表并在所测对象两端；测量电流时，应将表串入电路。
三、试验电路：
试验<1> 图
四、操作步骤：
（１）调节ZH－12实验台上的稳压电源，使其输出电压为９V，待用。
（２）（２）按图<1>所示电路图接线。
（３）（３）经教师检查后接通电源，用万用表测电压及各支路电流，并将结果填入表<1>中。
五、结果汇总
六、结果分析
1、分析试验电路(1)中各电流的关系
2、分析试验电路(1)中各段电压的关系
七、评分
１、操作是否符合规范（40%）
２、结果是否正确（30%）总分：_________
３、分析是否正确（30%）
课题7：基尔霍夫定律
课型：讲练结合
教学目的：
知识目标：
（１）掌握基尔霍夫定律。
（２）学会运用基尔霍夫定律进行电路分析。
技能目标：
（1）进一步熟悉万用表测量电压、电流的方法。
（2）进一步熟练电路连接技巧。
重点、难点：
重点：（1）基尔霍夫电压和电流定律的内容及表达式。
难点：（１）运用基尔霍夫定律分析电路。
（２）列方程∑Ｉ＝0、∑Ｕ＝0过程中，电流，电压，电动势字母前正负号的确
定。
教学分析
本节课采用学生先根据电路及要求进行试验，在课堂讲解过程中老师再加以演示，边演示边讲解，导出基尔霍夫定律的具体内容及表达式，再详细讲解在列ＫＣＬ、ＫＶＬ方程式中，电流，电压，电动势字母前正负号的确定，通过例题讲解，使学生能较好的理解课程
的内容，突破难点。
复习、提问：
（１）电路开路及短路时的特点？
（２）什么是简单电路？
教学过程：
一、引入
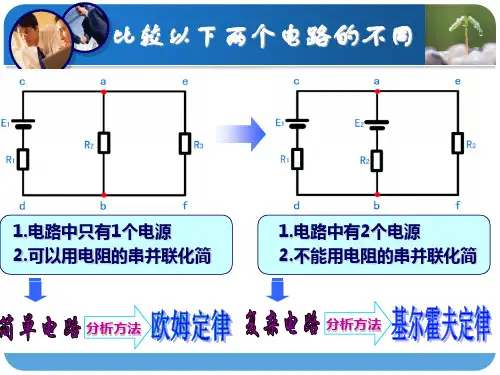
问题：简单电路是指可以用元件的串、并联加以化简求解的电路，复杂电路是指不能用元件的串、并联化简得以求解的电路，
如下图所示电路。
图1 （提问2-3人，引起大家对本次课题的注意）
引入正题：解决这一类问题可以用基尔霍夫定律，基尔霍夫定律有两部分，分别是基尔霍夫电流定律——阐述节点电流之间的关系；基尔霍夫电压定律——阐述回路电压之间的关系。
通过基尔霍夫电流、电压定律，针对上述电路中的节点和回路分别列出方程，再对方程加以求解，就可以解决上面提出来的问题。
那么，基尔霍夫定律究竟是什么呢？下面我们通过同学们自己的试验、测试来探索得出其具体内容。
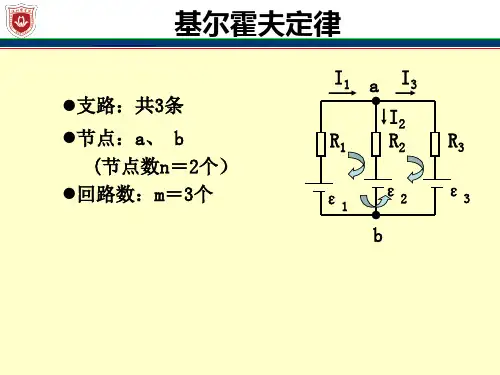
为了叙述方便，先对节点、支路、回路三个概念作一下解释。
（1）支路——无分支的一段电路，支路中各处电流相等，称为支路电流。
（2）节点——三条或三条以上支路的连接点。
（3）回路——由一条或多条支路所组成的闭合电路。
请学生回答图1中的支路、节点、回路数。
二、试验操作
提示注意事项，做好电路连接示范，按试验操作单对项目1进行连接测试，并记录好所
测量的数据。
三、对试验结果进行分析
1、对节点电流关系进行分析
先通过提问，请同学们回答从他们的测试结果中获得什么发现，提问2-3人。
I1+I2=I3
或改写为I1+I2-I3 = 0 =>∑I=0
即表示：在任一瞬间，一个节点上电流的代数和恒等于零。
（分析：先确定电流的正方向，如果规定正方向向着节点的电流取正号，那么背着节点的电流就取负号）为什么？因为电荷在电路中任何一点均不能堆积，这是由电流的连续性所决定。
得出结论：
基尔霍夫电流定律（KCL）：在任一瞬间，流向某一节点的电流之和等于流出该节点的
电流之和。
∑ I入=∑I出
2、对回路电压进行分析
提问2-3人，请同学们回答从他们的测试结果中发现了什么。
从左回路看，沿顺时针方向，是否有
U ab+U bc+U ca=0 =>∑U=0
从右回路看，沿顺时针方向是否有U ad+ U db+U ba =0 =>∑U =0把U用E来代替，因从数值上有U =E
左回路式子可写成U ab+U bc-E=0 =>U ab+U bc=E =>∑E=∑（IR）（因U ca沿顺时针方向是电压下降方向，而E沿这个方向是电压上升，所以E前面要加“--”号）即在任一回路循行方向上，回路中的电动势的代数和等于电阻上电压降的代数和。
首先，假设电流的正方向与回路循行方向，对于式∑E=∑（IR），凡电流方向与回路循行方向相同时，取正，相反时，取负。
电动势的正方向与所选回路循行方向一致者，取正号，相反者，取负号。
得出结论：
基尔霍夫电压定律（KVL）：在任一瞬间，沿任一回路循行方向，回路中各段电压
的代数和恒等于零。
原因：电路中任意一点的瞬时电位具有单值性（同一点同一时间不可能有两个电位值）
四、基尔霍夫定律的推广应用
1、基尔霍夫电流定律可扩展应用于任一闭合面。
结论：在任一瞬间，通过任一闭合面电流的代数和也恒等于零。
基尔霍夫定律通常应用于节点。
但对于图2中由三个电阻三角形连接所组成的电路，我们给它在外面画一个虚线圆圈；这个虚线圆圈就引成了一个闭合面。
我们可以把闭合面看成一个“广义节点”，基尔霍夫电流定律同样适用于广义节点。
我们也可以用基尔霍夫电流定律，写出A、B、C三个节点的
电流关系，从而推导出流入闭合面的电流关系：
根据基尔霍夫电流定律有：I A=I AB-I CA
I B=I BC-I AB
I C=I CA-I BC 图2
把上列三式相加即得I A+ I B+ I C=0 =>∑I=0
即，任一瞬间，通过任一闭合面的电流的代数和也恒等于零。
根据这一原理，基尔霍夫电流定律还可以推广应用到其它一些场合。
例如：
例1：一个晶体三极管有三个电极，各极电流的方向如图所示，各极电流关系如何？
解：晶体管可看成一个闭合面
则有I E =I B+ I C I B
I C
I E
例2：两个电气系统若用两根导线连接，如图3（a），电流I1和I2的关系如何？若用一根导线连接，如图3（b），电流I是否为零？
解：将A电气系统视为一个广义节点，则对图a有I1=I2
对图b则有I=0
图3（a）图3（b）解：将A电器系统看作一个广义节点。
则对图3（a）：I1=I2；对图3（b）：I=0。
结论：基尔霍夫电流定律可推广应用于广义节点。
2、基尔霍夫电压定律扩展应用于回路的部分电路
如果把并未闭合的回路AOBA看成一个虚拟的闭合回路。
则U AB+U B -U A =0 => U AB=U A-U B
同理，我们来看一下一段有源电路的欧姆定律表达式：
U=E-IR0
图4
可见用欧姆定律与基尔霍夫定律解答是一致的；所以基尔霍夫定律可以应用于简单或复杂的一切电路。
下面再举一个基尔霍夫电压定律应用的例子。
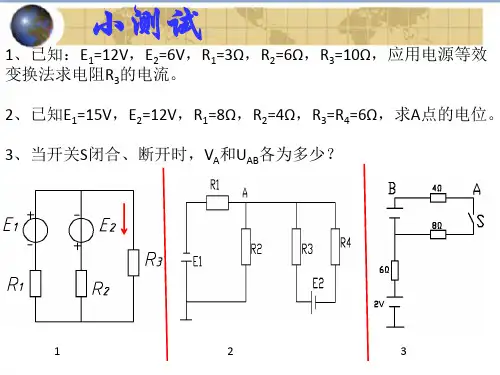
例3：在下图所示电路中，已知U1=10V，E1=4V，E2=2V，R1=4Ω，R2=2Ω，R3=5Ω，1、2两点间处于开路状态，试计算开路电压U2。
解：对左回路应用基尔霍夫电压定律可得：
E1=I（R1+R2）+U1
得：I=(E1- U1)/（R1+R2）=-1A
再对右回路列出：
E1-E2=IR1+U2
得：U2=E1-E2-IR1=6V
小结：基尔霍夫定律包括电流定律和电压定律两部分。
电流定律是描述电路中节点电流关系的。
指出任一瞬间，流入节点的电流恒等于流出节点的电流。
同时，电流定律还可推广应用于广义节点。
电压定律是描述回路电压之间的关系的。
它指出，在任一瞬间，沿任一回路循行方向，回路中各段电压的代数和恒等于零。
同时，电压定律也可推广应用于回路的部分电路。
基尔霍夫定律反映的是任何电路，任何元件之间的电压电流关系。
通过列出描述节点电流关系的方程和描述回路电压之间关系的方程，并联解之，就可获得电路中电流电压的相关解答。
它是描述电路中电流电压关系的最基本的定律，同学们必须对其内容有深刻的理解，并会应用本定律于电路物理量的求解。
作业：见参考书1，第43页2-19、2-29。
