SPSS相关分析

第10章相关分析 (225)1 双变量相关分析 (225)1.1 双变量相关分析的数据特征 (225)1.2 皮尔逊相关系数 (225)1.3 肯德尔相关系数 (228)1.4 例题3 (230)2 偏相关关系 (232)2.1 偏相关关系 (232)2.2 例题 (232)3 距离相关分析 (234)3.1 特征 (234)3.2 主要参数 (235)3.3 例题 (235)3.4 实例介绍 (237)第10章相关分析相关分析是研究变量之间关系密切程度的一种统计方法，包括双变量相关分析、偏相关分析和距离相关分析。

1 双变量相关分析1.1 双变量相关分析的数据特征当某一个事物存在着多个变量时，而各个变量之间呈数量关系时，可以用双变量相关分析来研究，并做出统计学推断。

双变量相关分析可以输出两两变量之间的相关系数，相关系数的种类有皮尔逊相关系数、肯德尔相关系数、斯皮尔曼等级相关系数等。

1.2 皮尔逊相关系数X和Y有线性函数关系，两变量间的相关系数是+1～-1，相关系数没有单位。

1.2.1 例题133名产妇进行产前检查，测定X1-X6六项指标，试计算X1-X4的皮尔逊相关系数。

1.2.2 SPSS过程Data，analyze，correlate，打开bivariate对话框，选择x1-x4→variables，选择pearson 相关系数，two-tail，flag significant correlations，打开options对话框，means and standard deviations，exclude case pairwirs，continue，ok.two-tail，双尾检验；Flag significant correlations：用星号显示有显著性相关的相关系数；Exclude case pairwirs：剔除有缺失值的配对变量；Cross-product deviations and covarances：显示每一对变量的离均差交叉积与协方差。

第8章SPSS的相关分析学习目标：1.明确相关关系的含义以及相关分析的主要目标。

2.掌握散点图的含义，熟练掌握绘制散点图的具体操作。

3.理解简单相关系数、Spearman相关系数、Kendall相关系数的基本原理，熟练掌握计算各种相关系数的具体操作，能够读懂分析结果。

4.理解偏相关系分析的主要目标以及与相关分析之间的关系，熟练掌握偏相关分析的具体操作，能够读懂分析结果。

8.1 相关分析相关分析是分析客观事物之间关系的数量分析方法，明确客观事物之间有怎样的关系对理解和运用相关分析是极为重要的。

客观事物之间的关系大致可归纳为两大类关系，它们是函数关系和统计关系。

相关分析是用来分析事物之间统计关系的方法。

所谓函数关系指的是两事物之间的一种一一对应的关系，即荡一个变量x取一定值时，另一变量y可以依确定的函数取唯一确定的值。

例如，商品的销售额与销售量之间的关系，在单价确定时，给出销售量可以唯一地确定出销售额，销售额与销售量之间是一一对应的关系，且这个关系可以被y=Ρx（y表示销售额，Ρ表示单价，x表示销售量）这个数学函数精确地描述出来。

客观世界中这样的函数关系有很多，如圆面积和圆半径、出租车费和行程公里数之间的关系等。

另一类普遍存在的关系是统计关系。

统计关系指的是两事物之间的一种非一一对应的关系，即当一个变量x取一定值时，另一变量y无法依确定的函数取唯一确定的值。

例如，家庭收入和支出、子女身高和父母身高之间的关系等。

这些事物之间存在一定的关系，但这些关系却不能像函数关系那样可用一个确定的数字函数描述，且当一个变量x取一定值时，另一变量y的值可能有若干个。

统计关系可再进一步划分为线性相关和非线性相关关系。

线性相关又可分为正线性相关和负线性相关。

正线性相关关系指两个变量线性的相随变动方向相同，而负线性相关关系指两个变量线性的相随变动方向相反。

事物之间的函数关系比较容易分析和测度，而事物之间的统计关系却不像函数关系那样直接，但确实普遍存在，并且有的关系强，有的关系弱，程度各有差异。

相关系数是衡量变量之间相关程度的度量，也是很多分析的中的当中环节，SPSS 做相关分析比较简单，主要是区别如何使用这些相关系数，如果不想定量的分析相关性的话，直接观察散点图也可以。

相关系数有一些需要注意的地方：1、两变量之间存在相关，仅意味着存在关联，并不意味着因果关系。

2、相关系数不能进行加减乘除运算，没有单位，不同的相关系数不可比较3、相关系数大小容易受到数据取值区间大小和数据个数大小的影响。

4、相关系数也需要进行检验确定其是否有统计学意义相关系数的假设检验中H0：相关系数=0，变量间没有相关性H1：相关系数≠0，变量间有相关性相关系数很多，我们一般根据变量的类型进行选择，我们知道变量类型由低级到高级可以分为定类、定序、定距、定比四种类型，而变量的数据类型则可以分为连续型或者离散型，注意不要混淆一、定距、定比变量，基本上也就是连续变量一般使用pearson相关系数，也称为积差相关系数，是一种线性相关系数，使用最为广泛，适用条件是两变量需要为线性关系，并且都来自正态分布总体，且要求成对出现二、定序、定距、定比变量一般使用spearman等级相关系数也称为秩相关系数，该系数利用了变量的次序信息，而且对原始数据没有过多要求，因此比pearson相关系数使用范围更广，它利用两变量的秩次大小作为分析依据，也可以认为是基于秩次的pearson相关系数，当数据不符合pearson相关系数的要求时，可以选择使用spearman相关系数，但是如果是定距或定比变量，还是建议用pearson相关系数，spearman 相关系数的效能略低。

三、只限定序变量1.Gamma相关系数2.Kendall等级相关系数，分为τ-a，τ-b，τ-c三种3.Somer's D相关系数四、定类变量定类变量的相关性大都是根据卡方值衍生而来1、person卡方实际上也就是卡方检验2.列联系数3.φ-Phi系数4.Cramer's V系数mbda（λ）系数6.Goodman and Kruskal的Tau-y系数五、二分类变量1.相对危险度RR值2.优势比OR值=========================================================熟悉了各种相关系数的情况之后，我们来看一下在SPSS中的操作1.分析—描述性统计—交叉表此过程一般用来分析列联表的，由于数据的组成大多是列联表形式，因此该过程包含了很多种相关系数2.分析—相关—双变量此分析为简单相关分析，是最常用的相关分析。

SPSS相关分析实例操作步骤-SPSS做相关分析SPSS（Statistical Product and Service Solutions）是目前在工业、商业、学术研究等领域中广泛应用的统计学软件包之一。

Correlation是SPSS的一个功能模块，可以用于分析两个或多个变量之间的关系。

下面是SPSS进行相关分析的具体步骤：1. 打开SPSS软件，选择“变量视图”（Variable View），输入相关的变量名，包括数字型变量和分类变量。

2. 进入“数据视图”（Data View），输入数据，并保存数据集。

3. 打开菜单栏中的“分析”（Analyze），选择“相关”（Correlate），再选择“双变量”（Bivariate）。

4. 在双变量窗口中，选择包含需要分析的变量的变量名，并将其移至右侧窗口中的变量框（Variables）。

5. 如果需要控制其他变量的影响，可以选择“控制变量”（Options）。

6. 点击“确定”（OK）按钮后，SPSS将输出结果，并将其显示在输出窗口中。

相关系数（Correlation Coefficient）介于-1和1之间，可以用来衡量两个变量之间的线性关系的强度。

7. 如果需要对结果进行图形化展示，可以选择“图”（Plots），并选择适当的图形类型。

需要注意的是，进行相关分析时需要确保变量之间存在线性关系。

如果变量之间存在非线性关系，建议使用其他统计方法进行分析。

同时，SPSS进行相关分析的结果只能描述变量之间的关系，不能用于说明因果关系。

以上是SPSS做相关分析的具体步骤，希望能对大家进行SPSS 数据分析有所帮助。

spss对数据进行相关性分析实验报告一、实验目的与背景在统计学的研究中，相关性分析是一种常见的分析方法，用于研究两个或多个变量之间的关联程度。

本实验旨在使用SPSS软件对收集到的数据进行相关性分析，并探索变量之间的关系。

二、实验过程1. 数据收集：根据研究目的，我们收集了一份包含多个变量的数据集。

其中，变量包括A、B、C等。

2. 数据准备：在进行相关性分析之前，我们需要对数据进行准备。

首先，我们载入数据集到SPSS软件中。

然后，对于缺失数据，我们根据需要采取相应的填补或删除策略。

接着，我们进行数据的清洗和整理，以确保数据的准确性和一致性。

3. 相关性分析：使用SPSS软件，我们可以轻松地进行相关性分析。

在SPSS的分析菜单中，选择相关性分析功能，并设置相应的参数。

我们将选择Pearson相关系数，该系数用于衡量两个变量之间的线性相关关系。

此外，还可以选择其他类型的相关系数，如Spearman相关系数，用于非线性关系的探索。

设置参数后，我们点击“运行”按钮，即可得到相关性分析的结果。

4. 结果解读：SPSS将为我们提供一份详细的结果报告。

我们可以看到每对变量之间的相关系数及其显著性水平。

如果相关系数接近1或-1，并且P值低于显著性水平（通常为0.05），则可以得出两个变量之间存在显著的线性相关关系的结论。

此外，我们还可以通过散点图、线性回归等方法进一步分析相关性结果。

5. 结论与讨论：根据相关性分析的结果，我们可以得出结论并进行讨论。

如果发现两个变量之间存在显著的相关关系，我们可以进一步探究其原因和意义。

同时，我们还可以提出假设并设计更深入的实验，以验证和解释这些相关性。

三、结果与讨论根据我们的研究目的和数据集，通过SPSS软件进行的相关性分析显示了一些有意义的结果。

我们发现变量A与变量B之间存在显著的正相关关系（Pearson相关系数为0.7，P<0.05）。

这表明随着A的增加，B也会相应增加。

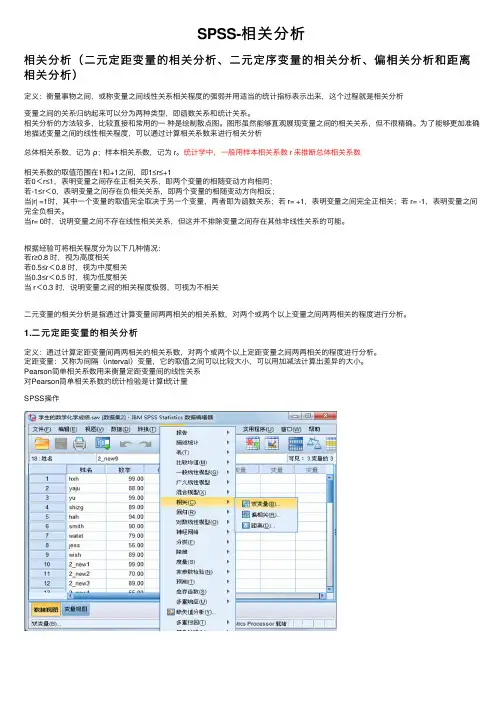
SPSS-相关分析相关分析（⼆元定距变量的相关分析、⼆元定序变量的相关分析、偏相关分析和距离相关分析）定义：衡量事物之间，或称变量之间线性关系相关程度的强弱并⽤适当的统计指标表⽰出来，这个过程就是相关分析变量之间的关系归纳起来可以分为两种类型，即函数关系和统计关系。

相关分析的⽅法较多，⽐较直接和常⽤的⼀种是绘制散点图。

图形虽然能够直观展现变量之间的相关关系，但不很精确。

为了能够更加准确地描述变量之间的线性相关程度，可以通过计算相关系数来进⾏相关分析总体相关系数，记为ρ；样本相关系数，记为 r。

统计学中，⼀般⽤样本相关系数 r 来推断总体相关系数相关系数的取值范围在1和+1之间，即1≤r≤+1若0＜r≤1，表明变量之间存在正相关关系，即两个变量的相随变动⽅向相同；若-1≤r＜0，表明变量之间存在负相关关系，即两个变量的相随变动⽅向相反；当|r| =1时，其中⼀个变量的取值完全取决于另⼀个变量，两者即为函数关系；若 r= +1，表明变量之间完全正相关；若 r= -1，表明变量之间完全负相关。

当r= 0时，说明变量之间不存在线性相关关系，但这并不排除变量之间存在其他⾮线性关系的可能。

根据经验可将相关程度分为以下⼏种情况：若r≥0.8 时，视为⾼度相关若0.5≤r＜0.8 时，视为中度相关当0.3≤r＜0.5 时，视为低度相关当 r＜0.3 时，说明变量之间的相关程度极弱，可视为不相关⼆元变量的相关分析是指通过计算变量间两两相关的相关系数，对两个或两个以上变量之间两两相关的程度进⾏分析。

1.⼆元定距变量的相关分析定义：通过计算定距变量间两两相关的相关系数，对两个或两个以上定距变量之间两两相关的程度进⾏分析。

定距变量：⼜称为间隔（interval）变量，它的取值之间可以⽐较⼤⼩，可以⽤加减法计算出差异的⼤⼩。

Pearson简单相关系数⽤来衡量定距变量间的线性关系对Pearson简单相关系数的统计检验是计算t统计量SPSS操作2.⼆元定序变量的相关分析定序变量：⼜称为有序（ordinal）变量、顺序变量，它取值的⼤⼩能够表⽰观测对象的某种顺序关系（等级、⽅位或⼤⼩等）Spearman和Kendall's tua-b等级相关系数⽤以衡量定序变量间的线性相关关系，它们利⽤的是⾮参数检验的⽅法。

第八章SPSS的相关分析和线性相关分析在统计学中，相关分析是用来研究两个或多个变量之间关系的一种方法。

SPSS（Statistical Package for the Social Sciences）是一款常用的统计软件，可用于进行相关分析和线性相关分析。

本章将介绍如何使用SPSS进行相关分析和线性相关分析，以及如何解释分析结果。

一、相关分析相关分析是一种用于研究变量之间关系的统计方法。

通过相关分析可以确定两个或多个变量之间的关联程度，以及这种关联程度的方向（正相关或负相关）。

在SPSS中进行相关分析的步骤如下：1.打开SPSS软件，选择“文件”>“打开”>“数据”，选择要进行分析的数据文件，点击“打开”。

2.在菜单栏中选择“分析”>“相关”>“双变量”或“多变量”。

3. 在弹出的对话框中，将变量移动到“变量”框中。

可以选择自定义相关性系数的类型，如Pearson相关系数、Spearman相关系数等。

4.点击“OK”进行相关分析。

5.SPSS将生成一个相关矩阵和一个相关系数表格，展示了变量之间的关联程度。

在进行相关分析时，需要注意以下几点：1.相关系数的取值范围为-1到1，-1表示完全负相关，1表示完全正相关，0表示没有相关性。

2.根据相关系数的取值大小可以判断变量之间的关联程度，一般认为相关系数大于0.7为强相关，0.3到0.7为中等相关，小于0.3为弱相关。

3.相关分析只能判断变量之间是否存在关系，不能确定因果关系。

线性相关分析是一种用于研究两个变量之间线性关系的统计方法。

通过线性相关分析可以确定两个连续变量之间的关联程度，以及这种关联程度的方向（正相关或负相关）。

在SPSS中进行线性相关分析的步骤如下：1.打开SPSS软件，选择“文件”>“打开”>“数据”，选择要进行分析的数据文件，点击“打开”。

2.在菜单栏中选择“分析”>“相关”>“双变量”。

SPSS第十三讲相关性分析相关性分析是统计学中非常重要的概念，用于研究两个变量之间的关系。

SPSS是一种统计分析软件，可以用来进行相关性分析并且生成相应的结果。

本文将介绍SPSS中的相关性分析方法，并结合实际案例来解释其应用。

首先，打开SPSS软件并导入需要分析的数据。

假设我们有一组数据包含两个变量：X和Y。

我们想要确定这两个变量之间的相关性。

第一步是选择"分析"菜单中的"相关"子菜单。

在相关菜单中，我们可以看到有两个选项："二变量"和"相关矩阵"。

如果我们只想要分析两个变量之间的关系，就选择"二变量"。

在"二变量"对话框中，我们需要选择要分析的两个变量，即X和Y。

将它们分别输入到对应的方框中。

首先，选择X变量并将其拖到框中，然后选择Y变量并将其拖到框中。

在"协方差矩阵"部分，可以选择是否要计算协方差矩阵。

协方差矩阵会给出每个变量之间的协方差，是相关性的衡量指标之一、如果我们只关心相关性，可以不勾选该选项。

然后，点击"确定"按钮生成相关性分析结果。

SPSS会输出相关性系数，如皮尔逊相关系数和斯皮尔曼相关系数。

皮尔逊相关系数用于度量两个连续变量之间的线性相关性，而斯皮尔曼相关系数则用于度量两个有序变量之间的相关性。

除了相关系数，SPSS还会输出显著性水平（p值）。

p值用来衡量样本相关系数是否代表总体相关系数。

通常情况下，如果p值小于0.05，则我们可以认为样本相关系数是显著的。

接下来，我们将通过一个实际案例来说明相关性分析在SPSS中的应用。

假设我们想要研究体重和身高之间的相关性。

我们收集了100个人的身高和体重数据，现在想要分析这两个变量之间的关系。

首先，将身高数据输入到X变量中，将体重数据输入到Y变量中。

然后，在"协方差矩阵"部分不勾选选项，因为我们只关心相关性。

第七章SPSS的相关分析SPSS是一种常用的统计分析软件，可以进行各种统计分析方法，如相关分析。

相关分析是一种用来研究两个变量之间关系的方法。

本文将介绍SPSS中进行相关分析的方法和步骤。

进入“Correlate”选项后，弹出一个新的窗口，在这个窗口中有两个选项：“Bivariate”和“Partial”。

在这里我们选择“Bivariate”选项，因为我们想要研究两个变量之间的直接关系。

然后，我们可以选择要进行相关分析的变量，将其移动到右边的“Variables”框中。

在“Bivariate”选项的窗口中，还有一个选项“Options”，点击这个选项可以设置一些其他的参数。

比如我们可以选择是否计算缺失值、是否使用Spearman相关系数等。

根据实际情况，我们可以酌情选择这些参数。

在设置完成后，点击“OK”按钮，SPSS将进行相关分析，并且将结果显示在“Output”窗口中。

在输出结果中，我们可以看到相关系数的值以及相关系数的显著性水平。

此外，SPSS还会生成相关系数的散点图，方便我们直观地观察变量之间的关系。

除了进行简单的两个变量之间的相关分析，SPSS还可以进行多个变量之间的相关分析。

在“Bivariate”选项的窗口中，我们可以选择多个变量，将其移动到右边的“Variables”框中。

然后，我们可以选择是否计算偏相关系数，以及是否进行Bonferroni校正等。

总结起来，SPSS是一种方便易用的统计分析软件，可以进行各种统计分析方法，包括相关分析。

通过SPSS，我们可以快速而准确地对变量之间的关系进行研究。

在分析结果中，SPSS还会为我们提供有用的图表和统计指标，帮助我们更好地理解和解释数据。

SPSS相关分析实验报告篇一：spss对数据进行相关性分析实验报告实验一一.实验目的掌握用spss软件对数据进行相关性分析，熟悉其操作过程，并能分析其结果。

二.实验原理相关性分析是考察两个变量之间线性关系的一种统计分析方法。

更精确地说，当一个变量发生变化时，另一个变量如何变化，此时就需要通过计算相关系数来做深入的定量考察。

P值是针对原假设H0：假设两变量无线性相关而言的。

一般假设检验的显著性水平为0.05，你只需要拿p值和0.05进行比较：如果p值小于0.05，就拒绝原假设H0，说明两变量有线性相关的关系，他们无线性相关的可能性小于0.05；如果大于0.05，则一般认为无线性相关关系，至于相关的程度则要看相关系数R值，r越大，说明越相关。

越小，则相关程度越低。

而偏相关分析是指当两个变量同时与第三个变量相关时，将第三个变量的影响剔除，只分析另外两个变量之间相关程度的过程，其检验过程与相关分析相似。

三、实验内容掌握使用spss软件对数据进行相关性分析，从变量之间的相关关系，寻求与人均食品支出密切相关的因素。

(1)检验人均食品支出与粮价和人均收入之间的相关关系。

a.打开spss软件，输入“回归人均食品支出”数据。

b.在spssd的菜单栏中选择点击，弹出一个对话窗口。

C.在对话窗口中点击ok,系统输出结果，如下表。

从表中可以看出，人均食品支出与人均收入之间的相关系数为0.921，t检验的显著性概率为0.000<0.01，拒绝零假设，表明两个变量之间显著相关。

人均食品支出与粮食平均单价之间的相关系数为0.730，t检验的显著性概率为0.000<0.01，拒绝零假设，表明两个变量之间也显著相关。

(2)研究人均食品支出与人均收入之间的偏相关关系。

读入数据后：A.点击系统弹出一个对话窗口。

B.点击OK，系统输出结果，如下表。

从表中可以看出，人均食品支出与人均收入的偏相关系数为0.8665，显著性概率p=0.000<0.01，说明在剔除了粮食单价的影响后，人均食品支出与人均收入依然有显著性关系，并且0.8665<0.921，说明它们之间的显著性关系稍有减弱。

怎么用SPSS进行相关分析相关分析是一种用来确定两个或多个变量之间关系的统计方法，其中一个比较常见的使用软件是SPSS。

在SPSS中进行相关分析包括计算相关系数以及进行显著性检验。

以下是一步一步的指导，如何使用SPSS进行相关分析。

第一步：导入数据首先，打开SPSS软件，然后导入要进行相关分析的数据集。

点击“文件”菜单，选择“打开”子菜单，然后选择数据集的位置并导入数据。

第二步：选择变量在SPSS中，要选择进行相关分析的变量，首先需要将这些变量放入一个变量列表中。

点击顶部菜单的“数据”选项，然后选择“选择变量”。

在弹出的对话框中，选择要进行相关分析的变量，并将它们添加到变量列表中。

可以通过按住Ctrl键同时点击变量名称，以选择多个变量。

在SPSS中进行相关分析的最常用方法是使用“相关”功能。

点击顶部菜单的“分析”选项，然后选择“相关”子菜单。

在弹出的对话框中，将要进行相关分析的变量从“可用变量”框拖放到“相关变量”的框中。

然后，可以选择计算Pearson相关系数或Spearman相关系数，也可以选择计算双尾还是单尾显著性。

点击“确定”按钮后，SPSS将计算相关系数，并在输出窗口中显示结果。

第四步：解释结果分析结果将显示在输出窗口中。

可以找到Pearson相关系数（或Spearman相关系数）和相应的显著性水平。

Pearson相关系数的取值范围在-1到1之间，接近1表示正相关，接近-1表示负相关，接近0表示无相关。

通过分析结果，可以得出结论并解释变量之间的关系。

可以引用结果中的显著性水平，以确定变量之间的关系是否具有统计学意义。

第五步：可视化结果（可选）如果需要，可以使用SPSS的绘图功能可视化相关分析的结果。

点击顶部菜单的“图表”选项，然后选择适当的图表类型，例如散点图或线图。

通过分析图表，可以更直观地观察变量之间的关系。

总结：使用SPSS进行相关分析通常包括导入数据、选择变量、进行相关分析、解释结果以及可视化结果。

《数据统计分析软件SPSS的应用(五)——相关分析与回归分析》篇一数据统计分析软件SPSS的应用（五）——相关分析与回归分析一、引言在当今的大数据时代，数据统计分析成为了科学研究、市场调研、社会统计等众多领域的重要工具。

SPSS（Statistical Package for the Social Sciences）作为一款功能强大的数据统计分析软件，被广泛应用于各类数据分析中。

本文将重点介绍SPSS 中相关分析与回归分析的应用，以帮助读者更好地理解和掌握这两种分析方法。

二、相关分析1. 相关分析的概念与目的相关分析是研究两个或多个变量之间关系密切程度的一种统计方法。

其目的是通过计算相关系数，了解变量之间的线性关系强度和方向，为后续的回归分析提供依据。

2. SPSS中的相关分析操作步骤（1）导入数据：将数据导入SPSS软件中，建立数据文件。

（2）选择分析方法：在SPSS菜单中选择“分析”->“相关”->“双变量”，进行相关分析。

（3）设置变量：在弹出的对话框中，设置需要进行相关分析的变量。

（4）计算相关系数：点击“确定”后，SPSS将自动计算两个变量之间的相关系数，并显示在结果窗口中。

3. 相关分析的注意事项（1）选择合适的相关系数：根据研究目的和数据特点，选择合适的相关系数，如Pearson相关系数、Spearman相关系数等。

（2）控制混淆变量：在进行相关分析时，要控制可能影响结果的混淆变量，以提高分析的准确性。

三、回归分析1. 回归分析的概念与目的回归分析是研究一个或多个自变量与因变量之间关系的一种预测建模方法。

其目的是通过建立自变量和因变量之间的数学模型，预测因变量的值或探究自变量对因变量的影响程度。

2. SPSS中的回归分析操作步骤（1）导入数据：同相关分析一样，将数据导入SPSS软件中。

（2）选择分析方法：在SPSS菜单中选择“分析”->“回归”->“线性”，进行回归分析。

SPSS学习笔记之——相关分析（Pearson、Spearman、卡方检验一、相关分析方法的选择及指标体系（一）两个连续变量的相关分析1、Pearson相关系数最常用的相关系数，又称积差相关系数，取值-1到1，绝对值越大，说明相关性越强。

该系数的计算和检验为参数方法，适用条件如下：（1）两变量呈直线相关关系，如果是曲线相关可能不准确。

（2）极端值会对结果造成较大的影响（3）两变量符合双变量联合正态分布。

2、Spearman秩相关系数对原始变量的分布不做要求，适用范围较Pearson相关系数广，即使是等级资料，也可适用。

但其属于非参数方法，检验效能较Pearson系数低。

（二）有序分类变量的相关分析有序分类变量的相关性又称为一致性，即行变量等级高的列变量等级也高，如果行变量等级高而列变量等级低，则称为不一致。

常用的统计量有：Gamma、Kendall的tau-b、Kendall的tau-c等。

（三）无序分类变量的相关分析最常用的为卡方检验，用于评价两个无序分类变量的相关性。

根据卡方值衍生出来的指标还有列联系数、Phi、Cramer的V、Lambda系数、不确定系数等。

OR、RR也是衡量两变量之间的相关程度的指标。

二、SPSS相关操作SPSS的相关分析散布在交叉表和相关分析两个模块中。

（1）交叉表过程如下图：以上的指标很全面，解释如下：（1）“卡方”复选框：为常用的卡方检验，适用于两个无序分类变量的检验。

（2）“相关性”复选框：适用于两个连续性变量的相关分析，给出两变量的Pearson相关系数和Spearman相关系数。

（3）“有序”复选框组：包含了一组反映有序分类变量一致性的指标，只能用于两变量均为有序分类变量的情况。

（4）“名义”复选框组：包含一组分类变量相关性的指标，有序和无序分类时都可使用，但变量为有序时，检验效能没有“有序”复选框组中的统计量高。

（5）Kappa：为内部一致性系数。

（6）风险：给出OR或RR值。