SPSS典型相关分析
- 格式:pdf
- 大小:329.33 KB
- 文档页数:16

典型相关分析的spss操作流程1.首先,打开SPSS软件并创建一个新的数据文件。
First, open the SPSS software and create a new data file.2.导入你要进行典型相关分析的数据到SPSS中。
Import the data for canonical correlation analysis into SPSS.3.确保数据变量的命名和类型是正确的。
Make sure the data variable names and types are correct.4.确认数据的缺失值情况,并进行适当的处理。
Check for missing values in the data and handle them appropriately.5.选择“分析”菜单中的“相关”选项。
Select the "Correlate" option from the "Analysis" menu.6.选择“典型相关”作为分析的方法。
Choose "Canonical Correlation" as the method for analysis.7.将想要进行分析的自变量和因变量添加到对应的框中。
Add the predictor and criterion variables to their respective boxes for analysis.8.确定是否需要进行变量的标准化处理。
Decide if standardization of variables is needed.9.点击“OK”开始进行典型相关分析。
Click "OK" to start the canonical correlation analysis.10.解释典型相关分析的结果和统计显著性。
Interpret the results and statistical significance of the canonical correlation analysis.11.对典型相关分析的结果进行图表展示。

如何在SPSS中实现典型相关分析什么是典型相关分析?典型相关分析是指对于两个变量集合,分别找出它们的主成分,使得两个主成分之间相关系数最大,称为典型相关分析,也叫双重主成分分析。
典型相关分析可用于研究两个变量集合之间的联系,特别是当变量集合具有相关结构时,可发现更深入的联系。
SPSS中如何实现典型相关分析?1.打开数据文件:首先要打开SPSS软件,然后点击“文件”选项卡,从下拉菜单中选择“打开”命令。
在弹出的打开文件对话框中选择自己的典型相关分析数据文件并打开。
2.设置典型相关分析:点击“分析”选项卡,在下拉菜单中选择“典型相关”命令。
在弹出的对话框中选择两组变量集合并输入相关变量的名称,然后点击“确定”按钮。
3.进行典型相关分析:在弹出的典型相关分析结果窗口中,SPSS会输出典型相关系数矩阵和变量权重矩阵,以及典型变量的相关性和累积方差贡献等信息。
4.结果解释:通过观察典型相关系数矩阵和变量权重矩阵,可发现两个变量集合之间的相关性状况。
同时,通过观察典型变量的相关性和累积方差贡献,获取变量集合对联结的贡献度和对典型变量的解释能力。
典型相关分析的应用实例举例来说,假设我们想研究人的身体状况与心理健康之间的关系。
我们将人的身体状况因素归为一组变量集(如身高、体重、BMI指数等),将人的心理健康因素归为另一组变量集(如焦虑得分、抑郁得分、快乐得分等),然后进行典型相关分析。
结果显示,两组变量集之间存在强关联,其中第一对典型变量是身高、体重、BMI指数、焦虑得分和抑郁得分;第二对典型变量是快乐得分、嗜睡得分和心境得分。
这些变量集代表两方面不同的人类特征。
因此我们可以得到人类身体和心理健康之间的关系非常密切。
典型相关分析是一种用于寻找两组变量集合之间关联的有用工具。
在SPSS中实现典型相关分析,需要首先打开数据文件,然后选择指定变量集合并进行典型相关分析。
最后通过观察典型相关系数矩阵、变量权重矩阵、典型变量的相关性和累积方差贡献等指标,来解释变量集合之间的关联状况。

SPSS典型相关分析案例典型相关分析(Canonical Correlation Analysis,CCA)是一种统计方法,用于研究两组变量之间的相关性。
它可以帮助研究人员了解两组变量之间的关系,并提供有关这些关系的详细信息。
在SPSS中,可以使用典型相关分析来探索两个或多个变量之间的关系,并进一步理解这些变量如何相互影响。
下面我们将介绍一个典型相关分析的案例,以展示如何在SPSS中执行该分析。
案例背景:假设我们有一个医学研究数据集,包含30名患者的多个生物标记物和他们的疾病严重程度评分。
我们希望了解这些生物标记物与疾病严重程度之间的关系,并查看是否可以建立一个线性模型来预测疾病严重程度。
以下是执行这个案例的步骤:第1步:准备数据首先,我们需要准备数据,确保所有变量都是数值型。
在SPSS中,我们可以通过检查数据集的描述性统计信息或查看变量视图来做到这一点。
第2步:导入数据在SPSS中,我们可以通过选择菜单中的"File"选项,然后选择"Open"来导入数据集。
我们应该选择包含待分析数据的文件,并确保正确指定变量的类型。
第3步:执行典型相关分析要执行典型相关分析,我们可以选择菜单中的"Analyze"选项,然后选择"Canonical Correlation"。
在弹出的对话框中,我们应该选择我们希望研究的生物标记物变量和疾病严重程度评分变量。
然后,我们可以选择一些选项,如方差-协方差矩阵、相关矩阵和判别系数,并点击"OK"执行分析。
第4步:解释结果完成分析后,SPSS将提供几个输出表。
我们应该关注典型相关系数和标准化典型系数,以了解两组变量之间的关系。
我们可以使用这些系数来解释生物标记物如何与疾病严重程度相关联,并找到最重要的变量。
此外,我们还可以使用SPSS提供的其他统计结果来进一步解释模型的效果和预测能力。
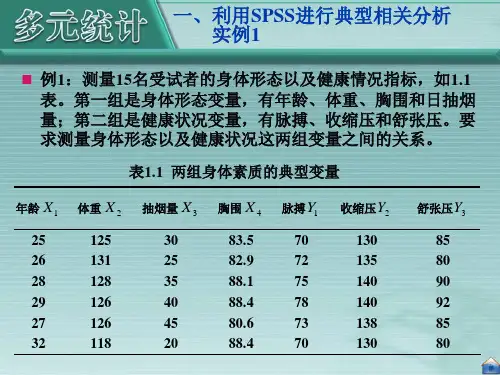


Correlations for Set-1Y1Y2Y3Y1 1.0000.9983.5012Y2.9983 1.0000.5176Y3.5012.5176 1.0000第一组变量间的简单相关系数Correlations for Set-2X1X2X3X4X5X6X7X8X9X10X11X12X13 X1 1.0000-.3079-.7700-.7068-.6762-.7411-.7466-.5922-.1948-.1285-.2650-.9070-.6874 X2-.3079 1.0000-.0117.0103-.0613-.0283-.0140.3333.4161.3810.3831.1098-.0640 X3-.7700-.0117 1.0000.9905.9860.9973.9990.5892.0421-.0196.2492.9515.9903 X4-.7068.0103.9905 1.0000.9910.9935.9952.5634.0249-.0367.2476.9120.9953 X5-.6762-.0613.9860.9910 1.0000.9887.9912.5717.0363-.0277.2475.8972.9926 X6-.7411-.0283.9973.9935.9887 1.0000.9985.5563.0142-.0453.2210.9355.9950 X7-.7466-.0140.9990.9952.9912.9985 1.0000.5795.0319-.0298.2441.9390.9945 X8-.5922.3333.5892.5634.5717.5563.5795 1.0000.7097.6540.8990.6619.5138 X9-.1948.4161.0421.0249.0363.0142.0319.7097 1.0000.9922.8520.1350-.0228 X10-.1285.3810-.0196-.0367-.0277-.0453-.0298.6540.9922 1.0000.8184.0752-.0801 X11-.2650.3831.2492.2476.2475.2210.2441.8990.8520.8184 1.0000.3093.1840 X12-.9070.1098.9515.9120.8972.9355.9390.6619.1350.0752.3093 1.0000.9040 X13-.6874-.0640.9903.9953.9926.9950.9945.5138-.0228-.0801.1840.9040 1.0000Correlations Between Set-1and Set-2X1X2X3X4X5X6X7X8X9X10X11X12X13 Y1-.7542-.0147.9995.9940.9892.9989.9998.5788.0334-.0280.2426.9430.9937 Y2-.7280-.0234.9965.9958.9954.9977.9988.5859.0485-.0136.2573.9285.9949 Y3-.4485.2952.5096.4955.5230.4760.5048.9695.7610.7071.9073.5449.4500Canonical Correlations1 1.0002 1.0003 1.000第一对典型变量的典型相关系数为CR1=1.....二三Test that remaining correlations are zero:维度递减检验结果降维检验Wilk's Chi-SQ DF Sig.1.000.000.000.0002.000.00024.000.0003.000103.48911.000.000此为检验相关系数是否显著的检验,原假设:相关系数为0,每行的检验都是对此行及以后各行所对应的典型相关系数的多元检验。

数学建模__SPSS_典型相关分析典型相关分析(Canonical Correlation Analysis)是一种多变量统计方法,用于分析两组变量之间的关系。
在典型相关分析中,我们尝试找到两组变量之间的线性组合,使得这些线性组合之间的相关性最大化。
典型相关分析可以帮助研究者理解两组变量之间的关系,并发现潜在的相关结构。
典型相关分析适用于有两组或多组相关变量的研究。
典型相关分析既可以用于预测模型的建立,也可以用于变量选择和降维。
下面我们将介绍典型相关分析的基本原理、步骤和应用。
典型相关分析的基本原理是寻找两个组合线性关系,使得两个组合相互之间具有最大的相关性。
在典型相关分析中,我们将一个变量集作为自变量,另一个变量集作为因变量,然后寻找这两个变量集之间的最佳线性组合。
典型相关分析的步骤如下:1.收集数据:首先需要收集自变量和因变量的数据。
这些数据可以是观察数据、实验数据或调查数据。
2.数据预处理:在进行典型相关分析之前,我们需要对数据进行预处理。
这包括缺失数据处理、异常值检测和变量归一化等步骤。
3.计算相关系数:接下来,我们需要计算自变量和因变量之间的相关系数。
这可以通过计算皮尔逊相关系数、斯皮尔曼相关系数或肯德尔相关系数来实现。
4.计算典型变量:通过应用典型相关分析模型,我们可以计算出一组自变量和一组因变量的典型变量。
典型变量是自变量和因变量的线性组合,它们具有最大的相关性。
5.进行相关性检验:在典型相关分析中,我们常常需要进行相关性的显著性检验。
这可以通过计算典型相关系数的显著性水平来实现。
6.结果解释和应用:最后,根据典型相关分析的结果,我们可以解释自变量和因变量之间的关系,并根据这些结果进行应用和决策。
典型相关分析的应用非常广泛。
例如,在金融领域,典型相关分析可以帮助分析公司的财务指标与市场指标之间的关系。
在医学研究中,典型相关分析可以用于分析不同变量对医疗结果的影响。
在社会科学研究中,典型相关分析可以帮助分析人们的行为和态度之间的关系。
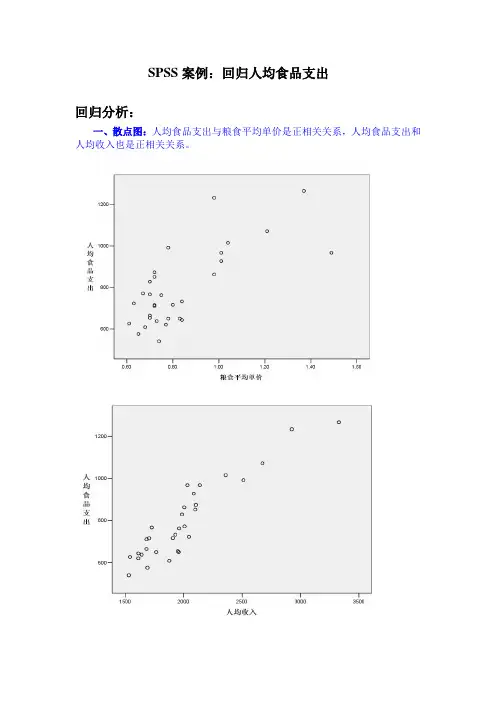
SPSS案例:回归人均食品支出回归分析:一、散点图:人均食品支出与粮食平均单价是正相关关系,人均食品支出和人均收入也是正相关关系。
二、相关性分析:人均食品支出与粮食平均单价的相关系数为0.730,为显著相关,假设检验t检验,sig(2-tailed)=0小于双侧检验的显著水平0.01,所以推翻原假设,人均食品支出与粮食平均单价线性相关。
人均食品支出与人均收入的相关系数为0.921,为显著相关,假设检验t检验,sig(2-tailed)=0小于双侧检验的显著水平0.01,所以推翻原假设,人均食品支出与人均收入线性相关。
三、(1)方程中的自变量列表(方法是进入)(2 )模型拟合概述:可以从表中看出,自变量和因变量之间的相关系数为0.940,拟合线性回归的确定性系数为0.883,经调整后的确定性系数为0.875,标准误的估计为2.766。
这里的R,R^2的值反映两变量的共变量比率高,模型与数据的拟合程度好。
Durbin-Watson=2.766>2,所以他们三者的关系程度显著。
四、方差分析:回归平方和为915129.1,残差平方和为120679.8,总平方和为1035809,对应的F统计量的值为106.164,显著性水平小于0.05,可以认为所建立的回归方程有效。
因为sig=0小于0.05,所以推翻原假设的多个自变量同时为0的假设,所以自变量不同时为0.五、回归系数:非标准化的回归系数X1的估计值为213.423,标准误为73.278,标准化的回归系数为0.243,回归系数显著性检验t统计量的值为2.913,对应显著性水平Sig.=0.007<0.05,可以认为粮食平均单价对人均食品输出有显著影响。
X2的估计值为0.352,标准误为0.038,标准化的回归系数0.767,回归系数显著性检验t统计量的值为9.185,对应显著性水平Sig.=0.000<0.05,可以认为人均收入对人均食品输出有显著影响。


SPSS学习笔记:探索相关分析方法(包括Pearson、Spearman 和卡方检验),了解如何运用这些统计工具揭示变量间的关联与独立性。
一、相关分析方法的选择及指标体系连续变量的两个相关分析1、Pearson相关系数最常用的相关系数,又称积差相关系数,取值-1到1,绝对值越大,说明相关性越强。
该系数的计算和检验为参数方法,适用条件如下:(1)两变量呈直线相关关系,如果是曲线相关可能不准确。
极端值会对结果造成较大影响。
(3)两变量符合双变量联合正态分布。
2、Spearman秩相关系数优化语序后的文本:对原始变量的分布不做要求、适用范围广泛,该方法不仅适用于等级资料,且对Pearson相关系数的应用场景有所扩展。
然而,作为非参数方法,它在检验效能上相较于基于参数的方法可能略显不足。
二:有序分类变量相关分析有序分类变量的相关性,即一致性,指的是:行变量等级高时,列变量等级亦高;反之,若行变量等级较高但列变量等级较低,则表现为不一致。
常用的统计量包括Gamma、Kendall的tau-b与tau-c。
(三)无序分类变量的相关分析最常用的为卡方检验,用于评价两个无序分类变量的相关性。
根据卡方值衍生出来的指标还有列联系数、Phi、Cramer的V、Lambda系数、不确定系数等。
OR、RR也是衡量两变量之间的相关程度的指标。
二、SPSS相关操作SPSS的相关分析散布在交叉表和相关分析两个模块中。
(1)交叉表过程如下图:以上的指标很全面,解释如下:(1)“卡方”复选框:为常用的卡方检验,适用于两个无序分类变量的检验。
相关性复选框适用于两个连续性变量的相关分析,提供两变量的Pearson及Spearman相关系数。
有序复选框组仅适用于两变量皆为有序分类变量,包含评估一致性指标。
(4)“名义”复选框组:包含一组分类变量相关性的指标,有序和无序分类时都可使用,但变量为有序时,检验效能没有“有序”复选框组中的统计量高。

SPSS典型相关分析结果解读
典型相关分析是SPSS的一种统计分析方法,用于检验两变量之间的线性关系。
它的结果包括Pearson积差相关系数、Spearman等级相关系数以及Kendall tau-b相关系数。
a. Pearson积差相关系数:Pearson积差相关系数是最常用的相关分析指标,该系数介于-1~+1之间,表示两个变量之间的线性关系强度。
当其值接近1时,表明两个变量之间呈正相关;当其值接近-1时,表明两个变量之间呈负相关;而当其值接近0时,表明两个变量之间没有显著相关性。
b. Spearman等级相关系数:Spearman等级相关系数也是一种常用的相关分析指标,用于检验两个变量之间的非线性关系,通常情况下,该指标的取值范围在-1~+1之间,其余与Pearson积差相关系数的解释原理相同。
c. Kendall tau-b相关系数:Kendall tau-b相关系数也是一种常用的相关分析指标,用于检验两个变量之间的非线性关系,其取值范围也是-1~+1,当取值为正时,表明两个变量之间存在正相关性;当取值为负时,表明两个变量之间存在负相关性;而当取值为0时,表明两个变量之间没有显著相关性。
SPSS典型相关分析及结果解释SPSS 11.0 - 23.0典型相关分析1方法简介如果要研究一个变量和一组变量间的相关,则可以使用多元线性回归,方程的复相关系数就是我们要的东西,同时偏相关系数还可以描述固定其他因素时某个自变量和应变量间的关系。
但如果要研究两组变量的相关关系时,这些统计方法就无能为力了。
比如要研究居民生活环境与健康状况的关系,生活环境和健康状况都有一大堆变量,如何来做?难道说做出两两相关系数?显然并不现实,我们需要寻找到更加综合,更具有代表性的指标,典型相关(Canonical Correlation)分析就可以解决这个问题。
典型相关分析方法由Hotelling提出,他的基本思想和主成分分析非常相似,也是降维。
即根据变量间的相关关系,寻找一个或少数几个综合变量(实际观察变量的线性组合)对来替代原变量,从而将二组变量的关系集中到少数几对综合变量的关系上,提取时要求第一对综合变量间的相关性最大,第二对次之,依此类推。
这些综合变量被称为典型变量,或典则变量,第1对典型变量间的相关系数则被称为第1典型相关系数。
一般来说,只需要提取1~2对典型变量即可较为充分的概括样本信息。
可以证明,当两个变量组均只有一个变量时,典型相关系数即为简单相关系数;当一组变量只有一个变量时,典型相关系数即为复相关系数。
故可以认为典型相关系1数是简单相关系数、复相关系数的推广,或者说简单相关系数、复相关系数是典型相关系数的特例。
2引例及语法说明在SPSS中可以有两种方法来拟合典型相关分析,第一种是采用Manova过程来拟合,第二种是采用专门提供的宏程序来拟合,第二种方法在使用上非常简单,而输出的结果又非常详细,因此这里只对它进行介绍。
该程序名为Canonical correlation.sps,就放在SPSS的安装路径之中,调用方式如下:INCLUDE 'SPSS所在路径\Canonical correlation.sps'.CANCORR SET1=第一组变量的列表/SET2=第二组变量的列表.在程序中首先应当使用include命令读入典型相关分析的宏程序,然后使用cancorr名称调用,注意最后的“.”表示整个语句结束,不能遗漏。
spss典型相关分析【SPSS典型相关分析】导言:典型相关分析是一种常用的统计方法,旨在研究两个不同变量集之间的关联程度。
通过典型相关分析,可以定量地了解两组变量之间的相互影响,从而更好地理解它们之间的关系。
本文将介绍SPSS软件在典型相关分析中的操作流程,并通过一个具体案例来展示对结果的解释和分析。
一、概述典型相关分析是一种多元回归技术,用于研究两组变量集之间的关系。
它通过构建线性组合(典型变量),从而发现两组变量之间的最大相关。
典型相关分析包含两个主要步骤:提取典型变量和解释典型变量。
二、SPSS操作流程1. 数据准备首先,需要确保所用数据集完整、无缺失值,并且变量之间没有共线性。
可以使用SPSS软件导入需要分析的数据集。
2. 创建数据文件在SPSS软件中,通过点击“文件”并选择“新建”来创建新的数据文件。
3. 导入数据在新的数据文件中,通过点击“文件”并选择“打开”来导入待分析的数据集。
在弹出的窗口中,选择所需导入的数据文件并点击“打开”。
4. 进行典型相关分析在SPSS软件中,点击“分析”并选择“典型相关”进行分析。
5. 设置变量在典型相关分析的窗口中,将两组变量逐一添加到相应的文字框中。
6. 运行分析确认所设置的变量无误后,点击“确定”运行分析。
7. 结果解释得出结果后,可以通过SPSS软件中提供的表格和图形等形式进行结果的解释和展示。
三、案例展示为了更好地理解典型相关分析的操作流程和结果解释,以下是一个具体案例的分析。
案例描述:研究人员想要了解大学生的学习成绩和心理健康之间的关系,他们收集了大学生的学习成绩(包括各科目的成绩和平均绩点)和心理健康指标(包括抑郁程度、压力水平和自尊水平)的数据。
分析步骤:1. 数据准备:研究人员清洗数据并确保数据集完整和无缺失值。
他们还进行了变量之间的相关性分析,以排除共线性。
2. 创建数据文件:研究人员在SPSS软件中创建了新的数据文件,命名为“大学生学习与心理健康”。
SPSS典型相关分析是一种通过分析一组变量与另一组变量之间的相关性来解释对方变量
差异的统计方法。
在企业管理和人力资源管
理领域,这种方法常被用来研究员工工作满
意度与各种因素的关系,并制定相关的管理
策略。
以下是一个SPSS典型相关分析的案例。
假设我们有一个样本,由100名员工组成,我们想要研究员工工作满意度与以下9个因
素之间的关系:薪酬、晋升机会、培训机会、福利、工作环境、工作内容、工作压力、同
事关系和公司文化。
在进行典型相关分析之前,我们需要将这些变量进行预处理,即去
除不需要的变量、处理缺失值和异常值等。
然后,我们进入SPSS软件,点击“Analyze”菜单下的“Canonical Correlation”命令,在打开的对话框中选择所有9个因素和员工
满意度作为“Variable(s)”并点击“OK”按钮。
SPSS会自动给出相应的结果,包括典型相关系数、方差解释比、典型相关变量等。
假设结果表明第一个典型相关系数为0.70,方差解释比为49%,前三个典型相关变量分别是薪酬、晋升机会和工作内容。
这意味着
这三个变量与员工工作满意度的关系最为密切,可以通过调整这些变量来提高员工的工
作满意度。
具体的建议可以根据调查结果和
实际情况制定,比如提高薪酬水平、加强晋升机会和职业发展支持、改善工作环境等。
我们已经知道,两个随机变量间的相关关系可以用简单相关系数表示,一个随机变量和多个随机变量的相关关系可以用复相关系数表示,而如果需要研究多个随机变量和多个随机变量间的相关关系,则需要使用典型相关分析。
典型相关分析由于研究的是两组随机变量之间的相关关系,因此也属于一种多元统计分析方法,多元统计分析方法基本上都有降维的思想,典型相关分析也不例外,它借用主成分分析的思想,在多个变量中提取少数几个综合变量,将研究多个变量间的相关关系转换为研究几个综合变量的相关关系。
典型相关分析首先在每组变量中寻找线性组合,使其具有最大相关性,然后再继续寻找在每组中寻找线性组合,使其在和第一次寻找的线性组合不相关的条件下,具有最大相关性,如此继续,直到两组变量的相关性被提取完为止,这些被提取的变量就是综合变量,也称为典型变量,第一对典型变量之间的相关系数称为第一典型相关系数,和其他多元分析一样,一般提取2-3对典型变量,就可以充分概括样本信息。
看一个例子我们现在想分析体力与运动能力的关系,随机抽取了38人,收集了与体力有关的7项指标,与运动能力有关的5项指标,数据如下SPSS对于典型相关分析没有专门的过程,而是需要调用专门的宏程序来加以完成,该程序名为Canonical correlation.sps,在按照SPSS的时候默认安装在Sample文件夹中相应的程序为:INCLUDE 'E:\Program Files\IBM\SPSS\Statistics\21\Samples\Simplified Chinese\Canonical correlation.sps'.CANCORR SET1=X1 to X7/ SET2=Y1 to Y5 .首先通过include命令读取宏程序,然后用cancorr调用程序主体并进行变量指定。
SPSS数据统计分析与实践
第二十二章:典型相关分析
(Canonical Correlation)
主讲:周涛副教授
北京师范大学资源学院
教学网站:/Courses/SPSS
典型相关分析(Canonical Correlation)本章内容:
一、典型相关分析的基本思想
二、典型相关分析的数学描述
三、SPSS实例
四、小节
典型相关分析的基本思想
z典型相关分析是研究两组变量之间相关关系的一种多元统计方法。
z简单相关系数;复相关系数;典型相关系数
z典型相关分析首先在每组变量中找出变量的线性组合,使其具有最大相关性;
z然后再在每组变量中找出第二对线性组合,使其与第一对线性组合不相关,而第二对本身具有最大相关性;
z如此继续下去,直到两组变量之间的相关性被提取完毕为止;
z这些综合变量被称为典型变量(canonical variates);第I对典型变量间的相关系数则被称为第I 典型相关系数(一般来说,只需提取1~2对典型变量即可较为充分的概括样本信息)。
典型相关分析的目的
T
q T
p Y Y Y Y X X X X )
,,,(),,,(2121K K ==设两组分别为p 与q 维(p ≤q)的变量X ,Y :
设p + q 维随机向量协方差阵,⎟⎟⎠⎞⎜⎜⎝
⎛=Y X Z ⎟⎟⎠
⎞
⎜⎜⎝⎛Σ
ΣΣΣ=Σ22
21
1211其中Σ11是X 的协方差阵,Σ22是Y 的协方差阵,Σ12=ΣT 21是X ,Y 的协方差阵
典型相关分析用X 和Y 的线性组合U =a T X , V =b T Y 之间的相关来研究X 和Y 之间的相关性。
其目的就是希望找到向量a 和b ,使ρ(U ,V )最大,从而找到替代原始变量的典型变量U 和V 。
典型相关分析的数学描述
z
典型相关系数的数学定义为:
b
b a a b
a V Var U Var V U Cov V U T T T 221112)()(),(),(ΣΣΣ=
=ρ由于随机变量乘以常数不改变其相关系数,为防止不必要的结果重复出
现,最好在其中附加如下的约束条件:
1
)(1)(2211=Σ==Σ=b b V Var a a U Var T T 记,,则有2112212111ΣΣΣΣ=−−A 12
11121122ΣΣΣΣ=−−B b Bb a Aa 22,λλ==其中既是A 又是B 的特征根,a 和b 就是对应于A 和B 的特征向量。
2
λ
SPSS 实例
为研究运动员体力与运动能力的关系,对某高一年级男生38人进行体力测试(共7项指标)及运动能力测试(共5项指标)。
运动能力测试指标:Y1 50米跑(秒)Y2跳远(cm )Y3投球(m )
Y4引体向上(次)Y5耐力跑(s )
体力测试指标:
X1反复横向跳(次)X2纵跳(cm )X3背力(kg )X4握力(kg )
X5台阶试验(指数)X6立定体前屈(cm )X7俯卧上体后仰(cm )
SPSS实例
SPSS操作
z SPSS采用’Canonical correlation.sps’宏程序来实现。
输出结果解释-两组变量间的相关系数SPSS在三个方框中分别输出的是体力测试指标内部的相关系数、运动能力测试指标内部的相关系数,以及两组指标间的相关系数
由体力测试指标内部相关系数看,各指标间相关系数较小,即指标间没有多大的重复。
如果两个指标相关系数很大,可能这两个指标反映的是同一个方面,可以考虑合并。
输出结果解释-两组变量间的相关系数SPSS在三个方框中分别输出的是体力测试指标内部的相关系数、运动能力测试指标内部的相关系数,以及两组指标间的相关系数
运动能力测试指标间的相关系数也比较类似(各指标间的相关系数较小),不过y2(跳远)和y4(引体向上)之间的相关系数较大,达到0.6067
输出结果解释-两组变量间的相关系数SPSS在三个方框中分别输出的是体力测试指标内部的相关系数、运动能力测试指标内部的相关系数,以及两组指标间的相关系数
上表输出的是体力与运动能力之间的相关系数,从二者直接相关系数看,只有X2(纵跳)和y2(跳远)之间关联程度较大(R=0.5584),而其他体力指标和运动能力指标间的直接关联不大,更多的可能是综合影响。
由于变量间的交互作用,因此,这个简单相关系数矩阵只能作为参考,不能真正反映两组变量间的实质联系。
典型相关系数及显著性检验
第一典型相关系数为0.763,第二典型相关系数为0.706,第三典型相关系数为0.607,它们均比体力指标和运动能力指标两组间的任一个相关系数大,即综合的典型相关分析效果要好于简单相关分析。
典型相关系数及显著性检验
由于此处的典型相关系数是从样本数据算得的,和简单相关系数一样,有必要进行总体系数是否为0的假设检验。
此处采用的是Bartlett的χ2检验,零假设为对应的典型相关系数为0。
上面的输出结果表明:在α=0.05的情况下,第一与第二典型相关系数是显著的。
典型变量的系数-体力变量
标准化变量(Standardized
Canonical Coefficients)的典型
相关变量的换算系数
e.g. 来自体力指标的第一典型变
量的计算公式为:
U1=0.314X1 + 0.628X2 +
0.295X3 + 0.309X4 + 0.335X5
+ 0.033X6 + 0.077X7
原始变量(Raw Canonical
Coefficients)的典型相关变量
的换算系数
典型变量的系数-运动能力变量
来自运动能力指标的第一典型变
量的计算公式为:
V1= -0.578y1 + 0.299y2 +
0.199y3 + 0.228y4 + 0.033y5
在第一对典型变量中,大部分变
量的系数都比较均匀,无论是体
力变量还是运动能力指标的系数
都表明,其测试结果越好,泽表
明其综合运动能力越强,可以解
释为全面能力程度。
典型变量的系数-运动能力变量
来自于体力指标的第二典型变量为:
U2 = 0.171X1-0.463X2 + 0.005X3 + 0.155X4
+0.841X5 + 0.146X6 -0.390X7
来自于运动能力指标的第二典型变量为:
V2 = -0.753y1 –1.087y2 -0.267y3
+ 0.038y4 –0.882y5
在对二对典型变量中,在体力指标中X2(纵跳)和X5(台阶试验)的系数较大,在运动能力指标中y1(50米跑)、y2(跳远)和y5(耐力跑)的系数较大,所以第二对典型变量可以解释为腿部能力的关系,表示跑和跳的能力。