当前位置：文档之家 › 第五章 2 围岩应力分析

第五章 2 围岩应力分析

  • 格式：doc
  • 大小：984.50 KB
  • 文档页数：44

下载文档原格式

  / 44

合集下载

n05 地下洞室的围岩应力与围岩压力汇总

n05 地下洞室的围岩应力与围岩压力汇总

5 地下洞室的围岩应力与围岩压力5.1 地下洞室的围岩应力计算及应力分布5.1.1 概述在岩体中开挖地下洞室，必然会破坏原来岩体内相对平衡的应力状态，并在一定范围内引起岩体天然应力状态的重分布。

岩体的强度和变形特性是否适应重分布以后的应力状态，将直接影响地下建筑物的安全。

为了正确评价地下建筑的稳定性，除进行必要的地质分析外，对围岩应力分布特征的分析和计算，也是评价围岩稳定性所必须的环节。

洞室开挖后，周围的岩石在一般情况下（侧压力系数<3）必然会在半径方向上发生伸长变形，在切线方向上发生压缩变形，这就使原来径向上的压缩应力降低，切向上的压缩应力增高，而这种降低和增高的程度随着远离洞壁逐渐减弱，达到一定距离后基本无影响。

通常将应力的这种变化称为应力重分布（即原始的应力状态变化到新的平衡的应力状态的过程）。

把应力重分布影响范围内的岩体称为围岩。

围岩内的应力称为围岩应力或二次应力（相对与天然应力）。

理论研究和实际测量结果表明，围岩应力的分布规律与开挖前岩体的天然应力状态及洞型等有关。

地下工程在设计、施工和使用时，总是要研究其稳定性问题。

在地下工程（井巷、隧道、洞室等）工作期内，安全和所需最小断面得以保证，称为稳定。

稳定如果用公式来表示的话，就是：Uu S <<max max σ 其中，σmax 、u max ——地下工程岩体或支护体中最大、最危险的应力与位移；S 、U ——岩体或支护材料的强度极限与位移。

无论无支护或有支护，凡涉及这方面研究的问题，统称为稳定性问题。

地下工程稳定性可分为两类：（1）自稳——能长期自行稳定的情况，如天然石灰岩溶洞、某些金属采矿场等。

通常不需要进行支护。

（2）人工稳定——需要依靠支护才能达到稳定的情况，如煤矿中的软岩巷道、表土洞室等，由于次生应力场的作用形成破碎带。

地下工程自身影响范围达不到地面的，称为深埋，否则称为浅埋。

深埋地下工程存在如下力学特点：（1）可视为无限体中的孔洞问题，孔洞各方向的无穷远处仍为原岩体；（2）当埋深Z 达到巷道半径或宽高之半的20倍及以上时，巷道影响范围内的岩体自重可忽略不计；原岩水平应力可以简化为均匀分布，通常误差不大（在10%以下）；（3）深埋的水平巷道长度较大时，可作为平面应变问题处理。

岩石力学巷道围岩应力分布及其稳定性分析

岩石力学巷道围岩应力分布及其稳定性分析
二、巷道围岩弹性区次生应力分析
基本假设： ①围岩为均质，各向同性、线弹性、无蠕变或粘性行为。 ②巷道长度远远大于巷道断面尺寸，符合平面变形条件。 ③巷道深度远远大于巷道断面尺寸，因此可忽略巷道围岩自 重。
1、圆形巷道次生应力分布
2 4 a2 1 1 a a r q p 1 2 q p 1 4 2 3 4 cos 2 r 2 2 r r 4 a2 1 1 a q p 1 2 q p 1 3 4 cos 2 r 2 2 r


r r 0
b m a
椭圆形巷道周边次生应力分布随轴比的变化(λ =1/4)
轴比m=b/a
应力
5
1.15p 1.75p
4
1.25p 1.25p
3
1.42p 0.75p
2
1.75p 0.25p1Fra bibliotek2.75p
1/2
4.75p
1/3
6.75p
两帮中央 顶底板中央
-0.25p -0.50p -0.58p
三、相邻巷道间的相互影响规律
相邻巷道间的相互影响规律： ①、当巷道断面相同时，其相互影响的距离可定为巷道最大尺寸 的3—5倍，当受爆破影响时，可增大为4—6倍。 ②、当相邻巷道中心连线与最大主应力垂直时，巷道间岩柱的应 力集中程度增加；当连线与最大主应力一致时，应力集中程度降 低巷道可相互起到屏蔽作用。
3、矩形巷道次生应力分 布
4、直壁拱形巷道次生应力分布
弹性区围岩应力分布规律： ①、围岩应力中，其决定作用的因素是：原岩应力、侧压系数、 断面以及a/r等。 ②、形状对围岩应力的影响往往比断面大小更明显。 ③、不论何种形状的巷道，其围岩应力均随着远离孔边急剧下降， 而且应力集中程度越高，下降幅度越明显。 ④、圆形巷道应力集中程度最低，平直周边容易出现拉应力，拐 角处容易产生高剪应力。 ⑤、巷道的高宽比对围岩应力分布有重大影响，断面的尺寸应尽 量与最大来压方向一致。

构造地质学05第五章岩石力学性质

构造地质学05第五章岩石力学性质
一、库伦剪切破裂准则 所谓准则，指的是基本条件是什么，库伦指出， 假定材料的破坏，取决于最大剪切应力，按照 这个理论建立的条件是：
τｍａｘ＝ τ０ …（１）
τ０为抗剪强度极限
理论上，破裂面应沿最大剪应力面产生，形成棋 盘格式构造。剪裂角＜ ４５０？
库伦解释是岩石抗剪强度与剪应力和正应力有 关，因此将（１）式改为：
De/dt 常量
撤出应力
t0 t1 t2
t3
时间
永久应变
t4 t5
松弛——保持应变不变，应力随时间而减小。 （相当于降低了岩石的弹性极限） （1）、应力随时间减小，松弛速度急剧下降。 （2）、应力经很长时间后可趋于一极限值
实践证明：在地质上岩石能否在很长时间的极 小差异应力下不断变形，需要一定的温度和压 力条件，因为它一般发生在地壳深层或它具备 有利于蠕变之条件的地方，如某些强变形带中。
剪切 脆性
挠曲
压扁
流动 温度
韧性
熔融 围 压
岩石随P-T条件的变化而呈现 变形习性及相应的主要变形机制
显理 示想 了的 各地 构壳 造一 层段 次剖 构面 造， 样剖 式面
三．岩石变形的时间因素
在地质条件下，岩石变形是长期的，通常要 以百万年为单位，因此评价时间因素对岩石变 形的效应具有关键意义。
σｙ＝０
完全塑性材料。没
有载荷，变形继续
增大。
如果超过屈服点，继 续塑性变形，需施加 更大的应力超过屈服 应力，这个过程称应 变硬化或加工硬化。 经过一段应变硬化的 塑性变形后卸载，应 力－应变曲线回到e２ 表明总的永久变形。
应变硬化
σｙ＞０ σｙ＝０
如果将同样应力继续 加上去，应力－应变 曲线则沿以前路径回 到塑性变形Ｐ位置上 ，好像增大了弹性范 围和增高了屈服应力 （σｙ／）。因此应变 硬化可以看作屈服强 度随递进变形而连续 升高。

第五章岩石地下工程

第五章岩石地下工程

设原岩垂直应力为p，水平应力为q，作用在围岩边 界，忽略围岩自重的影响，按弹性理论中的基尔西公式 计算围岩中任一点A（r,θ）的应力：
p
q
q p
q p
p q a 2 q p a 2 a 4 r2(1 r2)2(1 4 r2 3 r4)c2 os
p q a 2 qp a 4 2(1 r2)2(1 3r4)c2 os
γ——围岩重度（kN/m3）。
在矿山法施工的条件下，ⅠⅡ类围岩取Hp=2.5hq ；ⅣⅤ类围岩 取Hp=2.0hq 。
3、地下工程按用途可分为： 交通地下工程（如公路及铁路隧道、水底隧道、
地下铁道、航运隧道、人行隧道等） 水工地下工程（如引水及尾水隧洞、导流隧洞、
排沙隧洞等） 市政地下工程（如给排水隧道、人防洞室等） 矿山地下工程。
3
当θ＝0，π时， p(3)
当θ＝ 3π/2 ，π/2时， p(31)
不同的λ下，坑道周边切向应力σθ 的分布：
λ
θ=0，π θ=π/2， 3π/2
4
－p
11p
3
0
8p
2
p
5p
1
2p
2p
1/2
2.5p
0.5p
1/3
2.67p
0p
1/4
2.75p
-0.25p
不同的λ下，坑道周边切向应力σθ 的分布：
(5－1)
rq 2p(12a r2 23a r4 4)si2 n
（2）当r＝a时，即坑道周边的应力为：
r r0
(5－3)
p ( 1 2 c2 o ) q ( 1 s 2 c2 o ) s
或：
p ( 1 ) 2 ( 1 ) c 2 o (5s －4)

围岩应力状态ppt课件

围岩应力状态ppt课件
3
分析问题的思路
①围岩的塑性判据； ②塑性区内围岩的应力应满足塑性判据和
平衡方程； ③弹性区内围岩的应力应满足弹性条件和
平衡方程； ④在弹塑性边界上即满足弹性条件又满足
塑性判据，且满足应力和位移的协调性
4
1. 围岩的塑性判据
摩尔-库仑条件作为塑性判据 ：
其塑性条件是，可以在-平面上表示
R0
R02 r2
teLeabharlann z 1 R02 r2
R0
R02
r2
对比式（3.3.11）
r t
z (1 2 ) pa 2
z
(1
2
)
pa
2
将两式相加消去σR0，得 re ＋ te ＝2 z
并应满足边界处塑性判据（式3.4.4）：
17
即求得弹、塑性区边界上（ r＝ R0 ） 的应力表达式。（式3.4.13）：
限制了塑性区域的发展。
20
讨论2：若坑道开挖后不修筑衬砌，即径向
支护阻力pa＝0时 的极端情况下塑性区是
最大的，式（3.4.16）（包含开挖半径和
围岩参数的表达式）；
1sin
R0
r0
(1
s
in
)
c cot c cot
z
2 sin
21
讨论3：若想使塑性区域不形成，即r0＝ R0时， 就可以由式（3.4.15）求出不形成塑性区所需 的支护阻力 ，式（3.4.17） ；
pa z (1 sin ) c cos
这就是维持坑道处于弹性应力场所需的最小支 护阻力。
对比式（3.4.13）
r t
z (1 sin ) c cos z (1 sin ) c cos

围岩应力状态

围岩应力状态

ccot
式3.4.10
2021/6/3
13
由式（3.4.10）中可知，
围岩塑性区内的应力值与初始应力状态 无关，
仅与围岩的物理力学性质、开挖半径及 支护提供的阻力有关。
为什么？
2021/6/3
14
（2）弹性区内的应力场
在塑性区域以外的弹性区域内，其应力状态是 由初始应力状态及塑性区边界上提供的径向应 力Leabharlann R0 决定的。2021/6/3
5
图3.4.1 材料强度包络线及应力圆
最大主应力 最小主应力 Rc的表达式
Rc
2cos 1sin
c
2021/6/3
6
塑性判据：式（3.4.3）或式（3.4.4）
tp ( 1 si) nr p ( 1 si) n 2 c co 0 s
tp rp R c 0 , 1 1 s s ii,n n R c 1 2 c s o ic n s
化。
设以岩体的残余粘聚力cr和残余内摩擦 角 r表示改变后的岩体特性，则（3.4.3）
式可写成式（3.4.6） 的形式。
tr rrr Rcr 0
2021/6/3
9
2. 轴对称条件下围岩应力的弹 塑性分析
塑性区内单元体的受力状态
2021/6/3
10
（1）塑性区内的应力场
塑性区内任一点的应力分量需满足平衡 条件。对于轴对称问题，不考虑体积力， 某一单元体极坐标平衡方程式 （3.4.7） ：
tr zz((1 1 ssii n n )) c cc co o s s 2R 0 zR 0
该应力式与围岩的初应力状态σz、围岩 本身的物理力学性质c、φ有关，而与支
护阻力pa和开挖半径r0无关。

围岩应力应变计算公式

围岩应力应变计算公式

围岩应力应变计算公式引言。

在岩石工程中，围岩的应力应变计算是非常重要的一部分。

通过对围岩的应力应变进行准确的计算，可以帮助工程师更好地了解围岩的稳定性，从而有效地设计和施工工程项目。

本文将探讨围岩的应力应变计算公式，以及如何应用这些公式来进行工程实践。

围岩的应力应变计算公式。

围岩的应力应变计算公式可以通过岩石力学理论来推导和建立。

在岩石力学中，通常使用弹性模型来描述岩石的应力应变关系。

弹性模型假设岩石在受力作用下会产生弹性变形，即在去除外力后能够完全恢复到原来的形状。

基于弹性模型，可以得到围岩的应力应变计算公式如下：ε = σ / E。

其中，ε表示围岩的应变，σ表示围岩的应力，E表示围岩的弹性模量。

这个公式表明了围岩的应变与应力之间的线性关系，弹性模量E越大，围岩的应变就越小。

应力应变计算公式的应用。

围岩的应力应变计算公式可以应用于岩石工程的各个方面，包括岩石的稳定性分析、隧道和坑道的支护设计、岩石爆破工程等。

下面将分别介绍这些方面的应用。

1. 岩石的稳定性分析。

在岩石工程中，经常需要对围岩的稳定性进行分析，以确保工程项目的安全性。

围岩的应力应变计算公式可以帮助工程师计算出围岩在受力作用下的变形情况，从而评估围岩的稳定性。

通过对围岩的应力应变进行分析，工程师可以确定围岩的变形情况，为工程项目的设计和施工提供重要的参考依据。

2. 隧道和坑道的支护设计。

在隧道和坑道工程中，围岩的应力应变计算公式可以用于支护结构的设计。

通过计算围岩的应力应变，工程师可以确定支护结构的尺寸和材料，以确保支护结构能够有效地抵抗围岩的变形和破坏。

应力应变计算公式还可以用于评估支护结构的稳定性，为支护设计提供科学依据。

3. 岩石爆破工程。

在岩石爆破工程中，围岩的应力应变计算公式可以用于评估爆破后围岩的变形情况。

通过计算围岩的应力应变，工程师可以确定爆破参数，以减小围岩的应力集中，降低围岩的破坏程度，从而提高爆破效果和保证工程安全。

岩石力学-岩石地下工程围岩应力解析法分析

岩石力学-岩石地下工程围岩应力解析法分析

2）基本方程：
平衡方程：
d r r 0
dr
r
本构方程（平面应变）：
r

1
E
2
( r
1

)


1 2
E
(
1
r)
几何方程：
r

du dr

u r
3）边界条件
r R0 , r 0 r , r p0
4）结果


u (1 ) p0R02 p0R02
Er

1 2
(1


)
p0
(1

2
R02 r2
3
R04 r4
)
sin
2
（6－28）
3）讨论
① 1 时，式（6-28）变为


p0 (1
R02 r2
)
r

p0 (1
R02 ) r2
②周边应力情况 r R0 时，r r 0有
r 0
(1 ) p0 2(1 ) p0 cos 2 （6－29）
由 d 0 d
得
m 1

（6-31）
将此m值代入（6-30）得到
p0 p0 （6-32）
4、矩形和其他形状巷道周边弹性应力 常见的非圆巷主要有梯形、拱顶直墙、椭圆、
拱顶直墙反拱等。
1）基本解题方法 原则上，地下工程比较常用的单孔非圆巷围岩
的平面问题弹性应力分布，都可用弹性力学的复 变函数方法解决。
③径向位移常用计算式
轴对称圆巷：
u 1
E
p0
R02 r

隧道结构设计基本原理

隧道结构设计基本原理

（三）隧道工程的两大理论比较
松弛荷载理论
核心内容：稳定的岩体有自稳能力，不产生荷
载；不稳定的岩体则可能产生坍塌，需要用支护 结构予以支承。这样，作用在支护结构上的荷载 就是围岩在一定范围内由于松弛并可能塌落的岩 体重力。
代表人物：太沙基（K.Terzaghi）和普氏
围岩承载理论
以传统矿山法为基础
核心内容：围岩稳定显然是岩体自身有承载自
②以现场量测和实验室试验为主的实用设计方法，例如以洞周位量测 值为根据的收敛－约束法；
③作用与反作用模型，即荷载—结构模型，例如弹性地基圆环计算和 弹性地基框架计算等计算法；（结构力学模型）
④连续介质模型，包括解析法和数值法。数值计算法目前主要是有 限单元法。（岩体力学模型）
地下结构设计计算方法
结构力学方法 岩体力学方法 信息反馈方法 经验方法
稳能力；不稳定围岩丧失稳定是有一个过程的， 如果在这个过程中提供必要的帮助或限制，则围 岩仍然能够进入稳定状态。
代表人物：腊布希维兹、米勒·菲切尔、芬
纳·塔罗勃和卡斯特奈
以新奥法为基础
§5.2 围岩压力
一、围岩压力及其分类 二、影响围岩压力的因素 三、围岩松动压力的形成 四、确定围岩松动压力的方法 五、围岩压力的现场量测简介
对于围岩自身承载能力的认识有又分为两个阶段：
（1）假定弹性反力阶段 （2）弹性地基梁阶段
20世纪初期，假定弹性反力的分布 图形位置线为三角形或梯形 1934年，按结构的变形曲线假定地 层弹性反力的分布图形为月牙形
局部变形弹性地基梁理论
共同变形弹性地基梁理论
3.连续介质阶段
20世纪中期以来，连续介质力学理论
这种计算理论认为，作用在支护结构上的压力是其上覆岩层的重力， 没有考虑围岩自身的承载能力。

第五章岩体天然应力与洞室围岩的应力分布

第五章岩体天然应力与洞室围岩的应力分布
当构造应力存在时 1。
三.影响岩体初应力状态的其它因素
（1）地形-自重的减小或增大
地形对初应力的影响
（2）地质条件对初应力的影响。
背斜对地应力的影响
断层对地应力的影响
（3）水压力、热应力
孔隙水压力、流动水压力(影响小，可不计)、 静水压力（悬浮作用）热胀冷缩在岩体中产生 热应力。地温升高会使岩体内地应力增加，一
般地温梯度：3C/10m0岩体的体膨胀系
数： 10-5，岩体弹模E=104MPa；地温梯度 引起的温度应力约为：
T z E 0 .0 1 3 5 0 14 z 0M 0 .0 P z 0 a M 3
z--深度/m。
温度应力是同深度的垂直应力的1/9，并呈静 水压力状态。
四.岩体天然应力的分布特点和分布规律
二滩引水隧洞岩爆发生部位示意图
基坑边坡回弹错动
（5）野外原位测试测得的岩体物理力学指标比实验室岩 块试验结果高。
高地应力条件下岩体变形曲线
三、研究高地应力应注意的问题
（一）关于岩体的浅 塑状态
可以通过莫尔 强度包络线来判断 岩石（体）发生何 种破坏及形式。若 应力圆位于莫尔包 络线（图中曲线 2）以内，岩体处于
是工程稳定性分析的原始参数。 不仅影响场地的稳定性（区域性）；影响工程的设计 与施工（地下和地面工程）；同岩体力学特性有密切关系。
自重垂直应力分布
（2）Heim假设（塑性状态）
当原始应力超过一定的极限，岩体就会处 于潜塑状态或塑性状态。
1 （相当于 0.5）
（3）岩体为理想松散介质（风化带、断层带）
（二）处理高地应力的岩石力学原则 （1）及早发现，及早作出对应措施和准备工作。 （2）及早降低应力，释放能量。具体做法是：在开挖面 上及时打超前密集小孔；或从开挖面内向内钻孔和在一定 深度内放炮，在一定范围内形成破碎带，降低洞周的应力。 （3）及早采取临时性和永久性防护措施，使岩爆与施工 人员一定程度隔离开来。在设计支护结构时，宜设计柔性 支护。 （4）工程中设计一定的应力降低措施：切割应力释放槽， 尽量避免引起应力集中的开挖形态，避免不必要的小型叉 洞和形状突变的洞形。

第五章 2 围岩应力分析

第五章 2 围岩应力分析

四、 围岩应力分析地下洞室的开挖，会产生应力重分布，围岩应力不仅与天然应力场有关，而且还与洞室的开挖有关。

基本假定：①岩体均质，各向同性，连续体。

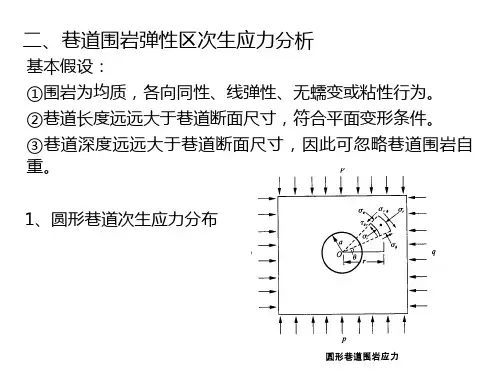
②无构造应力作用，仅由自重应力形成天然应力场，其大小为z z ⋅=γσ取K 0＝0，1/3，1三种情况下的应力场③忽略洞室高度上的应力场变化，即认为洞顶和洞底处的天然应力相同，则有H P v γ=（H 为洞中心的深度）④为平面应力问题K = 10P = P h vPv = r . Z1. 圆形洞室洞室开挖前的天然应力为H P v γ=v h P K P 0=围岩中的径向应力r σ，切向应力θσ以及剪应力θτr 可按下述公式计算：（Ⅰ）r0——洞室半径（m）r——自洞室中心算起的径向距离（m）θ——自水平轴算起的极坐标中的角度p v——垂直方向的压应力（MPa）（=γH）p h——水平方向的压应力（MPa）(= K0 p v)讨论：1)．K 0=1; p h =p v （K 0=1静水压力式的天然应力场） 洞室周围处于等压状态，（Ⅰ）式变为⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛-=011220220θθτσσr v v r r r p r r p ， 推出⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=-=011220220θθτσσr vvr r r p r r p取v rp σ或 vp θσ为应力集中系数，绘制应力集中系数分布曲线。

① σr 分布：洞室开挖后，围岩中的径向应力σr 始终小于岩体初始应力γH 。

即σr ＜P 0=γH②切向应力θσ大于v p ； 在洞壁上最大θσ=2P 0=2γH ③ 当r=6r 0时00611P P r ≈⎪⎭⎫ ⎝⎛-=σ 00611P P ≈⎪⎭⎫ ⎝⎛+=θσ离洞中心三倍洞直径的地方；其应力基本上为岩体的天然应力。

所以，洞室开挖的影响范围是三倍洞直径。

2)．K 0=0即0=h p ，仅有垂向应力（单向受压状态）从式中看，当r 一定时，r σ，θσ，θτr 是θ的函数， 讨论① 0=θ（水平方向）σr 分布⎥⎦⎤⎢⎣⎡-=44022023r r r rp v rσ 0r r =时，0=r σ 0r r >>时，0→r σ取04r r =，059.0=r σ05r r =，0384.0=r σ； 010r r =，0099.0=r σvr p σ对r 求导，得：02r r =，rH r 83=σ最大。

岩石力学-岩石地下工程围岩应力解析法分析

岩石力学-岩石地下工程围岩应力解析法分析
2）一般结论 和其他形状一样，在弹性应力条件下，巷道断
面围岩中的最大的应力是周边的切向应力，且周 边应力大小E，v弹性参数无关，与断面的绝对尺 寸无关。同样，它和原岩应力场分布、巷道的形 状很有关系。另外，断面在有拐角的地方往往有 较大的应力集中。
5、井巷围岩的弹性与粘弹性位移 1）弹性位移 ①特点：
由 d 0 d
得
m 1

（6-31）
将此m值代入（6-30）得到
p0 p0 （6-32）
4、矩形和其他形状巷道周边弹性应力 常见的非圆巷主要有梯形、拱顶直墙、椭圆、
拱顶直墙反拱等。
1）基本解题方法 原则上，地下工程比较常用的单孔非圆巷围岩
的平面问题弹性应力分布，都可用弹性力学的复 变函数方法解决。
③塑性区半径
（6－53） （6－54） （6－55）
6）讨论
① Rp与R0成正比，与p0成正变关系，与c， ，P1成
反变关系；
②塑性区内各点应力与原岩应力p0无关，且应力圆 均与强度曲线相切（注意联立方程中有屈服条件， 此为极限平衡问题特点之一）。
③支护反力P1=0，RP最大。 ④指数 1sin 物理意义，可近似理解为“拉压强度

1 2
(1


)
p0
(1

2
R02 r2
3
R04 r4
)
sin
2
（6－28）
3）讨论
① 1 时，式（6-28）变为


p0 (1
R02 r2
)
r

p0 (1
R02 ) r2
②周边应力情况 r R0 时，r r 0有
r 0

巷道围岩应力变化分析

巷道围岩应力变化分析

巷道掘进后，围岩的原岩应力平衡状态被破坏，围岩应力重分布进入塑性状态，一方面导致塑性区扩大和两帮位移增长，另一方面使一些强度低的岩石因应力达到强度极限而破坏，随之产生裂缝或剪切位移，造成破坏岩石的大量脱落，为了保持围岩，稳定以及硐室结构的安全，在围岩稳定性评价的基础上进行支护，以改变围岩的物理力学性质，改善围岩内部的应力及应力分布，降低支承压力区的承载能力，使支承压力向围岩深部转移，从而提高围岩的稳定性。

巷道掘进时，巷道围岩压力以压应力为主，在巷道两帮和拱脚处应力较大，容易出现应力集中，导致出现片帮和巷道拱脚岩石破裂。

顶板由于卸载作用，巷道出现最大切向拉应力，并分布在顶板一定范围内，极易出现顶板岩石离层现象。

施工巷道的围岩应力及来压分析

施工巷道的围岩应力及来压分析

施工巷道的围岩应力及来压分析施工巷道的围岩应力及来压是施工过程中需要重点分析和考虑的问题。

在进行施工工程之前，首先需要对巷道围岩进行调查和评估，确定巷道围岩的性质、厚度、倾角等基本参数。

然后，根据巷道的设计方案和施工工艺，结合现场的实际情况，进行应力及来压分析。

巷道的围岩应力分析是指对围岩的应力状态进行研究。

一般来说，巷道围岩的应力状态可以分为两种情况：一是围岩受到一定的外力作用而形成的应力状态；二是围岩失去平衡后自身产生的应力状态。

在施工巷道中，由于施工过程中的爆破、挖掘和支护等工作会对围岩产生应力作用，因此需要对这些外力作用进行分析和评估。

巷道围岩的来压分析是指对围岩受到力的压力大小进行分析。

在施工巷道中，围岩受到上部土层、建筑物及水压力等的压力作用，这些压力会对巷道的稳定性和安全性产生影响。

因此，需要对来压力进行分析和计算，确定巷道围岩的受力情况，为巷道设计和施工提供依据。

对于施工巷道的围岩应力及来压分析，可采用数值模拟方法进行研究。

通过建立巷道围岩的数学模型，输入相关参数和边界条件，使用计算机软件对围岩的应力和来压进行模拟计算。

根据计算结果，可以评估巷道围岩的稳定性，并提出合理的支护措施和安全预警机制。

在进行施工巷道围岩应力及来压分析时，应注意以下几个方面：一是要充分考虑巷道围岩的地质条件，包括岩性、结构、断裂、节理等因素；二是要准确测量巷道围岩的应力和来压，尽可能获取真实的数据；三是要合理选择适应的数值模拟软件和方法，确保计算结果的可靠性；四是要结合施工工艺和支护措施，进行综合分析和评估。

总之，施工巷道的围岩应力及来压分析是保证巷道工程顺利施工和安全运营的重要工作。

通过合理的分析和评估，可以为巷道设计和施工提供科学依据，保障巷道的稳定性和安全性。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

四、 围岩应力分析地下洞室的开挖，会产生应力重分布，围岩应力不仅与天然应力场有关，而且还与洞室的开挖有关。

基本假定：①岩体均质，各向同性，连续体。

②无构造应力作用，仅由自重应力形成天然应力场，其大小为z z ⋅=γσ取K 0＝0，1/3，1三种情况下的应力场③忽略洞室高度上的应力场变化，即认为洞顶和洞底处的天然应力相同，则有H P v γ=（H 为洞中心的深度）④为平面应力问题K = 10P = P h vPv = r . Z1. 圆形洞室洞室开挖前的天然应力为H P v γ=v h P K P 0=围岩中的径向应力r σ，切向应力θσ以及剪应力θτr 可按下述公式计算：（Ⅰ）r0——洞室半径（m）r——自洞室中心算起的径向距离（m）θ——自水平轴算起的极坐标中的角度p v——垂直方向的压应力（MPa）（=γH）p h——水平方向的压应力（MPa）(= K0 p v)讨论：1)．K 0=1; p h =p v （K 0=1静水压力式的天然应力场） 洞室周围处于等压状态，（Ⅰ）式变为⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛-=011220220θθτσσr v v r r r p r r p ， 推出⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=-=011220220θθτσσr vvr r r p r r p取v rp σ或 vp θσ为应力集中系数，绘制应力集中系数分布曲线。

① σr 分布：洞室开挖后，围岩中的径向应力σr 始终小于岩体初始应力γH 。

即σr ＜P 0=γH②切向应力θσ大于v p ； 在洞壁上最大θσ=2P 0=2γH ③ 当r=6r 0时00611P P r ≈⎪⎭⎫ ⎝⎛-=σ 00611P P ≈⎪⎭⎫ ⎝⎛+=θσ离洞中心三倍洞直径的地方；其应力基本上为岩体的天然应力。

所以，洞室开挖的影响范围是三倍洞直径。

2)．K 0=0即0=h p ，仅有垂向应力（单向受压状态）从式中看，当r 一定时，r σ，θσ，θτr 是θ的函数， 讨论① 0=θ（水平方向）σr 分布⎥⎦⎤⎢⎣⎡-=44022023r r r rp v rσ 0r r =时，0=r σ 0r r >>时，0→r σ取04r r =，059.0=r σ05r r =，0384.0=r σ； 010r r =，0099.0=r σvr p σ对r 求导，得：02r r =，rH r 83=σ最大。

θσ 分布4402202321rr r r p v ++=θσ 0r r =时，v p 3=θσ， 为最大切向应力0r r >>时，v p →θσ， 为岩体初始应力0=θτr ②θ=90°时r σ44022023251rr r r p v r+-=σ0r r =时，0=r σ 0r r >>时，v r p rH ==σ 06r r =时，v r p 9317.0=σ 010r r =时，v r p 97515.0=σ对v r p σ求导，得02.1r r =时，最小， 为拉应力，由于较小，一般未予考虑。

θσ 分布4402202321rr r r p v -=θσ 0r r =时，rH p v -=-=θσ出现拉应力。

03r r =时，0=θσ 03r r >时，0>θσ但很小如03r r =时，rH 271=θσ 05r r >时，0→θσ0=θτr③θ=45°r σ分布⎪⎪⎭⎫ ⎝⎛-=220121r r p v rσ 0r r =时，0=r σ 06r r >时，v r p 21≈σ θσ分布⎪⎪⎭⎫⎝⎛+=220121r r p v θσ 0r r =时，v p =θσ06r r >时，v p 21→θσ0=θτr⎪⎪⎭⎫ ⎝⎛-+=44022032121r r r r p v r θτ 0r r =时，0=θτr ： 02r r =时，v vr p p 65625.0169==θτ 03r r =时，v v r p p 5926.05432==θτ： 04r r =时，v r p 5566.0=θτ 05r r =时，v r p 5376.0=θτ： 06r r =时，v r p 5266.0=θτ 010r r =时，v r p 5098.0=θτ： 0r r >>时，vr p 21=θτ 对r 求导，得时，v r p 6667.0=θτ为最大13）K0=3(Ⅰ－3)讨论① 0θ=σ分布r⎪⎪⎭⎫ ⎝⎛-+=402032131r r r r p v rσ 0r r =时， 0=r σ 02r r =时， v r p 4375.0=σ03r r =时， v r p 395.0=σ04r r =时， v r p 371.0=σ 010r r =时， v r p 3399.0=σ0r r >> 时，h p =θσθσ 分布440220321rr r r p v ++=θσ 0r r =时，02r r =时， v p 229.1=θσ03r r =时， v p 086.1=θσ 04r r =时， v p 046.1=θσ 0r r >>时，v p =θσ0=θτr② 90=θ r σ44022021rr r r p v r+-=σ 0r r =时，0=r σ 02r r =时，v r p 5625.0=σ03r r =时，v r p 79.0=σ 04r r =时，v r p 879.0=σ05r r =时，v r p 9216.0=σ010r r =时，v r p 98.0=σ; 0r r >>时，v r p →σ 最大θσ分布⎪⎪⎭⎫ ⎝⎛-+=44022032131r r r r p v θσ 0r r =时，0=θσ；02r r =时，v p 4375.0=θσ； 03r r =时，v p 395.0=θσ 04r r =时，v p 371.0=θσ； 05r r =时，v p 3584.0=θσ010r r =时，v p 3399.0=θσ； 0r r >>时，v v p p 31333.0==θσ对r 求导，得03r r =时，v v r p p 444.094==σ 最大。

0=θτr ③θ=45°r σ 分布⎪⎪⎭⎫ ⎝⎛-=220132r r p v rσ 0r r = 时，0=r σ； 02r r =时，v r p 21=σ 04r r = 时，v r p 85=σ；010r r =时，v r p 66.0=σ02r r = 时，v r p 21=σ； 02r r =时，v r p 21=σ0r r >>时，v v r p p 667.032==σθσ分布⎪⎪⎭⎫ ⎝⎛+=220132r r p v θσ 0r r =时，v p 34=θσ； 02r r =时，v p 65=θσ； 03r r =时，v p 74.0=θσ 04r r =时，v p 708.0=θσ； 010r r =时，v p 673.0=θσ 0r r >>时，v v p p 667.032==θσθτr 分布⎪⎪⎭⎫ ⎝⎛-+=44022032131r r r r p v r θτ 0r r =时，0=θτr02r r =时，v r p 4375.0=θτ； 03r r =时，v r p 395.0=θτ 04r r =时，v r p 371.0=θτ； 05r r =时，v r p 3584.0=θτ 010r r =时，v r p 3399.0=θτ0r r >>时，v r p 31=θτ03r r =时，v v r p p 4445.094==θτ为最大综合上述讨论，有以下结论： ①无论K 0何值，洞壁上的径向应力σr =0 ；水平方向上，趋于水平应力的大小，如K 0=1时，σr =P h ;K 0=0时，σr =0; K 0=1/3时，σr =P h / 3;垂直方向上，趋于垂直应力的大小，即σr =P v ;不论 K 0=0，=1/3，或1。

② 不论K 0为任何值，洞壁上的剪应力0=θτr ，且在水平方向和垂直方向上的剪应力0=θτr ， 其它方向的剪应力不为零。

③关于洞壁上的切向应力θσ：a.在水平方向上（θ=0°），洞壁上的θσ随K 0值的增大而减小，b.在垂直方向上（θ=90°，洞顶）洞壁上的θσ随K 0值的增大而增大，且当310<k 时，出现拉应力。

c.当 K 0<1时，σθ随θ的增大（0→90而减小。

d.当K 0>1时，σθ随θ的增大而增大。

④围岩在洞壁上的各应力中，只有切向应力不为零，且最大切向应力发生在洞壁上。

⑤在围岩应力中，r σ，θτr 都小于v p ，而θσ可以大于v p稳定验算部位：侧墙和顶拱，验算的应力是切向应力θσ，压或拉。

如K 0=1时，验算θσ压。

K 0=0时，验算侧墙处压θσ＞r σ和顶拱θσ＞r σ。

出现拉应力的区域为： 120~90~60=θ2、椭圆形洞室椭圆形洞室两个半轴设为q 1、q 2，则参数方程为βcos 1a q x = βsin 2a q y =由于洞室围岩中的最大切向应力发生在洞壁上，则在稳定性分析需计算洞壁上的切向应力。

按弹性力学原理，开挖后所引起洞室边界上的切向应力为： (Ⅱ)21q q m =β——椭圆偏心角由于P v 、P h 为主应力，则0=xy τ 将m 代入（II ）并整理，得222222121222221sin )(2]sin ))[((q q q p q q q q q p p vh v t +-+-+-=ββσ（Ⅱ－1）与圆形洞室讨论一样，可取不同的q 1/q 2宽高比，讨论K 0取不同值时的变化（取β=0、45°、90°）讨论(1)．取宽高比25.0//21==q q h B A 点 （β=900）：K 0=0时，v t p -=σ（最大拉应力） K 0=1/3时，v t p 2=σ，压应力 K 0=1时，v t p 8=σ，压应力最大 B 点 （β=00）：v t p )2~0(=σ，K 0=0、1/3、1(2)．宽高比B/h=0.5 A 点（β=900）：00=k ，v t p -=σ拉应力 310=k ，v t p 21=σ10=k ，v t p 4=σB 点（β=00）：v t p )2~1(=σK 0 = 0、1/3、1（3）．宽高比B/h=2A 点（β=900）：K 0=0，σt = - p v ， K 0=1/3，v t p 31-=σ 拉应力 K 0=1，σt = p v B 点（β=00）：v t p )5~8.3(=σ 均为压应力。