比例尺(例1)

比例尺（1）【教学内容】比例尺（1）(教材第53页内容）。

【教学目标】1.从学生的生活实际出发认识比例尺，理解比例尺的含义，使学生会求一幅图的比例尺。

2.让学生经历比例尺的探究过程，体验从实践中学习的方法，感受数学知识与日常生活的密切联系，培养学生的探究意识和创新意识。

【重点难点】理解比例尺的含义。

【教学准备】投影仪，比例尺不同的地图，机器零件纸，北京的平面图。

【情景导入】教师：(出示两幅不同的地图，让学生思考两幅图中北京到上海中的距离一样吗？为什么不一样？因为它们的比例尺不一样。

这节课我们就一起来研究比例尺。

【新课讲授】1.比例尺的意义。

（1）教师讲解：因为在绘制地图和其它平面图时，经常要用到图上距离与实际距离的比，我们就把它起个名字，叫做比例尺。

（板书：图上距离：实际距离=比例尺）有时图上距离与实际距离的比也可以写成分数形式。

（板书： =比例尺） 图上距离是比的前项，实际距离是比的后项。

为了计算简便，通常把比例尺写成前项或后项是1的最简整数比。

（2）教师出示地图，引导学生观察1∶100000000。

（3）组织学生议一议：比例尺中的“1”表示什么?“100000000”表示什么？指名说一说：“1”表示图上距离，“100000000”表示实际距离，也就是说图上实际距离图上距离1cm 的距离表示实际距离100000000cm 。

教师说明：1∶100000000是数值比例尺，有时写成。

（4）引导学生观察比例尺。

适时讲解：这是线段比例尺，表示线段的长度1cm 是图上距离，50km 是实际距离，也就是说图上距离1cm 代表着实际距离是50km 。

（5）教师用投影出示图纸。

引导学生观察图中的比例尺2∶1表示什么? 指名汇报：2∶1表示图上距离是实际距离的2倍。

教师小结：在生产中，有时由于机器零件比较小，需要把实际距离扩大一定的倍数以后，再画在纸上。

这时比例尺的前项比后项大。

为了计算方便，通常把比例尺写成前项或后项是1的比。

比例尺例1：比例尺及其求法。

在教学例1之前，教材着重介绍了以下知识内容：比例尺的概念；比例尺的不同表示形式（数值比例尺和线段比例尺）及其线段比例尺转化为数值比例尺的方法（原实验教材以例1的形式编排）；沟通比例尺与分数的关系；除了用比例尺表示把实际距离缩小画在图纸上，还介绍了生活中把实际距离放大的情况等。

其中，教材强调在线段比例尺转化为数值比例尺时要特别注意单位的统一，再化简成最简成数比；另外，在用数值比例尺表示时，为便于计算，对一般的表示形式也做了特别的说明，即一般把比例尺写成前项或后项是1的形式。

之后的例1教学，就是根据比例尺的定义，介绍了比例尺的求法：利用图上距离和相对应的实际距离，先统一长度单位，再相比、化简。

例2：比例尺的应用。

教材提供了一个真实的问题情境：根据北京轨道交通路线示意图，求两站之间的实际距离。

教材给出了完整的解题过程：首先引导学生如何思考，再给出了从设未知数、列出比例以及解比例求出实际距离的具体过程。

在教学的过程中，特别要注意培养学生以下几方面的技能：在示意图上寻找比例尺的信息；经历并能反思求实际距离的思维过程：根据比例尺列出比例，解比例求出未知数的值，再换算成合适的单位。

例3：应用比例尺画平面图。

本例是综合运用比例尺、方位的有关知识解决实际问题。

与原实验教材相比，修订版教材提供了绘制简易位置的平面图，给出了比例尺，这大大降低了学生学习的难度。

【知识与技能】 使学生理解比例尺的意义并能正确地求出平面图的比例尺。

【过程与方法】使学生能够应用比例知识，根据比例尺求图上距离或实际距离。

【情感、态度与价值观】在探究过程体验成功的乐趣。

【教学重点】理解比例尺的意义，能根据比例尺正确求出图上距离或实际距离，画位置平面图。

【教学难点 】设未知数时长度单位的使用。

一、复习准备（一）填空。

1千米＝（ ）米1分米＝（ ）厘米1米＝（ ）分米1厘米＝（ ）毫米30米＝（ ）厘米300厘米＝（ ）分米15千米＝（ ）厘米40毫米＝（ ）厘米（二）解比例。

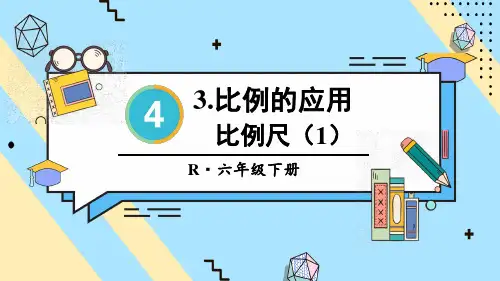
比例尺的三种公式(一)
比例尺的三种公式
1. 线性比例尺公式
•线性比例尺公式用于计算地图上物体的实际长度与地图上的表示长度之间的比例关系。

•公式：实际长度 = 地图上的表示长度× 比例尺分母
•举例：某张地图上标注的一段公路长度为5厘米，比例尺为1:10000，求实际公路长度。

解答：实际长度 = 5厘米× 10000 = 50000厘米 = 500米
2. 面积比例尺公式
•面积比例尺公式用于计算地图上物体的实际面积与地图上的表示面积之间的比例关系。

•公式：实际面积 = 地图上的表示面积× 比例尺分母的平方
•举例：某张地图上标注的一个湖泊面积为10平方厘米，比例尺为1:20000，求实际湖泊面积。

解答：实际面积 = 10平方厘米× ^2 = 平方厘米= 4平方千米
3. 体积比例尺公式
•体积比例尺公式用于计算地图上物体的实际体积与地图上的表示体积之间的比例关系。

•公式：实际体积 = 地图上的表示体积× 比例尺分母的立方
•举例：某张地图上标注的一座山的体积为立方厘米，比例尺为1:50000，求实际山的体积。

解答：实际体积 = 立方厘米× ^3 = 00立方厘米= 立方千米。

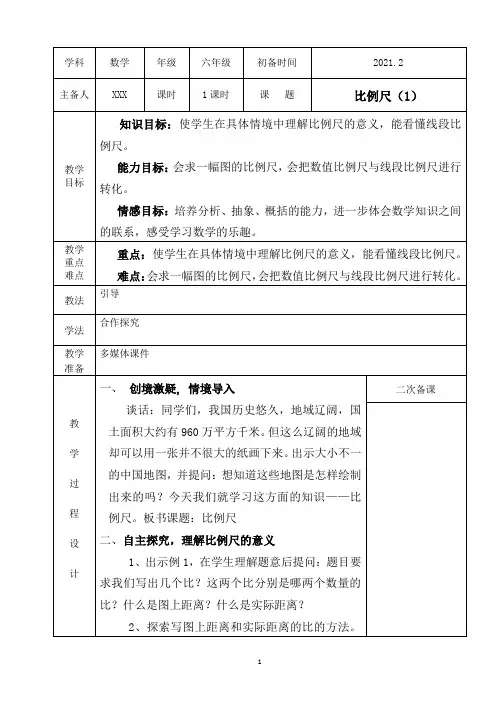
比例尺应用题参考答案典题探究一．基本知识点：二．解题方法：例1．在比例尺是1：500的图纸上，量得一个正方形草坪的边长是4厘米．这个草坪的实际面积是400平方米．考点：比例尺应用题．分析：图上距离和比例尺已知，依据“实际距离=图上距离÷比例尺”即可求出这个正方形草地的边长，进而利用正方形的面积S=a2，就能求出这个草坪的实际面积．解答：解：4÷=2000（厘米）=20（米），20×20=400（平方米）；答：这个草坪的实际面积是400平方米．故答案为：400平方米．点评：此题主要考查正方形的面积的计算方法依据图上距离、实际距离和比例尺的关系，解答时要注意单位的换算．例2．培正小学的操场长80米，宽50米，如果用的比例尺画出操场的平面图，图上面积是160平方厘米．考点：比例尺应用题．分析：实际距离和比例尺已知，依据“图上距离=实际距离×比例尺”即可分别求出操场长和宽的图上距离，进而利用长方形的面积公式就可以求出操场的图上面积．解答：解：80米=8000厘米，50米=5000厘米，8000×=16（厘米），5000×=10（厘米），16×10=160（平方厘米）；答：这个操场的图上面积是160平方厘米．故答案为：160平方厘米．点评：此题主要考查图上距离、实际距离和比例尺的关系在实际中的应用，以及长方形的面积的计算方法．例3．地图上1.5厘米的距离表示实际距离120千米，这幅地图的比例尺是1：8000000．如果该地图上，甲乙两地之间的图上距离是2厘米，那么实际距离是160千米．考点：比例尺应用题．专题：比和比例应用题．分析：（1）根据比例尺的意义作答，即图上距离与实际距离的比就是比例尺；（2）先求出1厘米的线段表示实际距离的千米数，由此求出2厘米所表示的实际距离的千米数．解答：解：（1）1.5厘米：120千米，=1.5厘米：12000000厘米，=15：120000000，=1：8000000；（2）120÷1.5×2，=80×2，=160（千米），故答案为：1：8000000；160．点评：本题主要灵活利用：比例尺=图上距离：实际距离这一关系解决问题．例4．在比例尺是1：4000000的地图上，量得甲、乙两港的距离是9厘米，一艘货轮于上午6时以每小时24千米的速度从甲港开往乙港，到达乙港的时间是晚上9或21时．考点：比例尺应用题；简单的行程问题．专题：比和比例应用题；行程问题．分析：先依据“实际距离=图上距离÷比例尺”求出两地的实际距离，再据“路程÷速度=时间”求出货轮从甲港到乙港需要的时间，进而可以求出到达乙港的时刻．解答：解：9÷=36000000（厘米）=360（千米），360÷24=15（小时），6+15=21（时）；答：货轮到达乙港的时间是晚上9时或21时．故答案为：晚上9或21．点评：此题主要考查图上距离、实际距离和比例尺的关系以及基本的数量关系“路程÷速度=时间”．演练方阵A档（巩固专练）1．一张图纸长30厘米、宽20厘米，把长50米、宽38米的一块长方形菜的画在这张图纸上，选用适当的比例尺是（）A．1：200 B．1：400 C．1：100 D．200：1考点：比例尺应用题．专题：比和比例应用题．分析：本题的实际长度是长50米、宽38米．而图上距离是：长30厘米、宽20厘米，要想画在这样的图纸上，必须是缩小的，所以D答案不能选，既能画下来，还能画的合适，这就是比例尺的问题了，应根据：图上距离：实际距离=比例尺来计算．解答：解：因为：50米=5000厘米38米=3800厘米，而图纸长30厘米、宽20厘米，比例尺为；30：5000≈1：167，20：3800=1：190，综合长和宽的比例尺选1：200比较合适．故选：A．点评：此题主要考查比例尺、图上距离、实际距离三者之间的数量关系：比例尺=图上距离÷实际距离，灵活变形列式解决问题．2．一个三角形中，三个内角的度数比是1：1：3，那么这个三角形是（）A．钝角三角形B．直角三角形C．锐角三角形D．等边三角形考点：比例尺应用题；三角形的分类；三角形的内角和．专题：比和比例应用题；平面图形的认识与计算．分析：因为三角形的内角度数和是180°，它的最大角占内角度数和的，根据一个数乘分数的意义，求出最大角，进而判断即可．解答：解：1+1+3=5，最大角度数：180°×=108°，所以，这个三角形是钝角三角形．故选：A．点评：解决此题关键是掌握三角形的内角度数和是180°，运用按比例分配的方法解决问题．3．在比例尺是1：8的图纸上，甲、乙两个圆的直径比是2：3，那么甲、乙两个圆的实际的直径比是（）A．1：8 B．4：9 C．2：3 D．8：1考点：比例尺应用题．分析：根据比例尺的意义，令甲乙两圆的图上直径为2d，3d，根据比例尺可得实际圆的直径分别是16d，24d，由此利用比例尺进行计算，即可选择正确答案．解答：解：令甲乙两圆的图上直径为2d，3d，根据比例尺可得实际甲乙两圆的直径分别是16d，24d，16d：24d=2：3．故选：C．点评：此题考查了利用比例尺解决实际问题的方法．4．学校实验园地是一个长60m，宽40m的长方形，用比例尺1﹕1000画平面图，长应画（）A．4cm B．6cm C．6dm D．6m考点：比例尺应用题．专题：压轴题；比和比例应用题．分析：图上距离=实际距离×比例尺，实际距离是60米，比例尺是1：1000．代入数据进行解答．解答：解：60米=6000厘米，6000×=6（厘米）．答：长应画6厘米．故选：B．点评：本题主要考查了学生对图上距离=实际距离×比例尺，这一数量关系的掌握情况．5．北京到上海的实际距离大约是300千米，画在一幅比例尺是的地图上，应该画（）厘米．A．3B．2C．6考点：比例尺应用题．专题：比和比例应用题．分析：因为图上距离1厘米表示实际距离50千米，依据除法的意义，即可求出图上距离．解答：解：300÷50=6（厘米）；答：应该画6厘米．故选：C．点评：此题主要考查线段比例尺的意义．6．在一幅比例尺是1：30000000的地图上，量的甲乙两地的距离是5厘米，那么甲地到乙地的实际距离是（）千米．A．150 B．6000 C．1500考点：比例尺应用题．专题：压轴题；比和比例应用题．分析：图上距离与比例尺已知，求实际距离，用图上距离除以比例尺即可．解答：解：5÷=150000000（厘米），150000000厘米=1500千米；答：甲地到乙地的实际距离是1500千米．故选：C．点评：本题主要是灵活利用比例尺的意义解决问题，注意单位的换算．7．一个直角三角形的两条直角边分别是3厘米、2厘米，按4：1的比例放大后，面积是（）平方厘米．A．6B．24 C．48 D．96考点：比例尺应用题．专题：压轴题．分析：先按4：1的比例尺分别求出放大后的两条直角边的长度，再依据三角形的面积公式即可求出放大后的面积．解答：解：放大后的直角边分别是：3×4=12（厘米），2×4=8（厘米）；放大后的面积：12×8÷2=48（平方厘米）；答：放大后的面积是48平方厘米．故选：C．点评：此题主要考查放大比例尺的应用及三角形的面积计算．8．在比例尺是1：500000的地图上，量得A、B两地间的距离是11厘米，A、B两地间的实际距离是（）千米．A．55 B．5500000 C．5500考点：比例尺应用题．专题：比和比例应用题．分析：求实际距离，根据公式“图上距离÷比例尺=实际距离进行解答即可．解答：解：11÷=5500000（厘米），5500000厘米=55千米，答：A、B两地之间的实际距离是55千米；故选：A．点评：此类题做题的关键是弄清题意，根据图上距离、实际距离和比例尺三者之间的关系进行列式解答．9．长江是中国第一大河，全长6300千米，在比例尺是1：100000000的地图上的长度为．（）A．6.3cm B．63dm C．63cm考点：比例尺应用题．专题：比和比例应用题．分析：根据比例尺=图上距离：实际距离，知道图上距离=比例尺×实际距离，代入数据解答即可．解答：解：6300千米=630000000厘米，630000000×=6.3（厘米），答：在比例尺是1：100000000的地图上的长度为6.3厘米．故选：A．点评：此题主要考查比例尺的意义及已知比例尺和实际距离求图上距离．注意单位的换算．10．一种精密零件长5毫米，把它画在图纸上，图上零件长6厘米，这张图纸的比例尺是（）A．1：12 B．5：6 C．6：5 D．12：1考点：比例尺应用题．专题：比和比例应用题．分析：根据比例尺=图上距离：实际距离，把实际长度5毫米，图上长度6厘米代入求出这张图纸的比例尺．解答：解：6厘米：5毫米，=60毫米：5毫米，=60：5，=（60÷5）：（5÷5），=12：1，答：这张图纸的比例尺是12：1．故选：D．点评：此题主要考查学生对比例尺这一知识点的理解和掌握，像这种求比例尺的题目单位一般不相同，因此首先要注意单位的统一．B档（提升精练）1．在比例尺是1：100000的地图上，量得甲、乙两地的距离是3厘米，甲、乙两地的实际距离是（）A．300千米B．3千米C．30千米D．0.3千米考点：比例尺应用题．专题：比和比例应用题．分析：图上距离和比例尺已知，依据“实际距离=图上距离÷比例尺”即可求出甲、乙两地的实际距离．解答：解：3÷=300000（厘米）=3（千米）；故选：B．点评：此题主要考查图上距离、实际距离和比例尺的关系，解答时要注意单位的换算．2．学校操场扩建后的平面图如图，扩建后面积比原来增加25%，操场原来的面积是（）平方米．A．480 B．4800 C．6000 D．7500考点：比例尺应用题；应用比例尺画图．专题：压轴题；比和比例应用题．分析：先依据“图上距离÷比例尺=实际距离”求出扩建后的操场的长和宽的实际长度，再利用长方形的面积公式求出扩建后的面积，把原来的面积看作单位“1”，再据已知一个数的几分之几是多少，求这个数的方法，即可求解．解答：解：6=6000（厘米）=60（米），10÷=10000（厘米）=100（米），100×60÷（1+25%），=6000÷1.25，=4800（平方米）；答：操场原来的面积是4800平方米．故选：B．点评：此题主要考查图上距离、实际距离和比例尺的关系，以及长方形的面积的计算方法在实际生活中的应用．3．新光小学的操场是一个长方形，画在比例尺是1：4 000的平面图上，长3厘米，宽2厘米．操场的实际面积是（）A．240平方米B．96平方米C．2.4平方米D．9 600平方米考点：比例尺应用题．专题：比和比例应用题．分析：要求操场的实际面积，根据“图上距离÷比例尺=实际距离”，代入数值，分别计算出操场实际的长和宽，然后根据“长方形的面积=长×宽”，代入数值，计算即可．解答：解：3÷=12000（厘米）=120（米），2÷=8000（厘米）=80（米），面积：120×80=9600（平方米），答：操场的实际面积是9600平方米，故选：D．点评：解答此题用到的知识点：（1）图上距离、实际距离和比例尺三者之间的关系；（2）长方形的面积计算方法．4．在比例尺是1：20的图纸上画出一种机械配件平面图的角是40度．这个角实际是（）度．A．2B．40 C．800考点：比例尺应用题．分析：比例尺=图上距离÷实际距离，是指长度尺寸按比例放大或缩小．解答：解：根据比例尺是1：20的图纸，知道图上距离是1厘米，实际距离是20厘米，是长度尺寸是按比例缩小，角的大小与边的长度无关，只与两边叉开的程度有关，所以角度是不会变的；故选：B．点评：此题主要考查了比例尺的意义以及角的意义．5．在比例尺是1：4000000的地图上，量得A、B两港距离为9厘米，一艘货轮于上午6时以每小时24千米的速度从A开向B港，到达B港的时间是（）A．15点B．17点C．21点考点：比例尺应用题．分析：先依据“实际距离=图上距离÷比例尺”求出两地的实际距离，再据“路程÷速度=时间”求出货轮从A地到B地需要的时间，进而可以求出到达B地的时刻．解答：解：9÷=36000000（厘米）=360（千米），360÷24=15（小时），6+15=21（时）；答：货轮到达B港的时间是21时．故选：C．点评：此题主要考查图上距离、实际距离和比例尺的关系以及基本的数量关系“路程÷速度=时间”．6．比例尺表示．A．图上距离是实际距离的B．实际距离是图上距离的800000倍C．实际距离与图上距离的比为1：800000考点：比例尺应用题．分析：在图上附有一条注有数目的线段，用它来表示和地面上相对应的实际距离，这就叫做线段比例尺．图中比例尺1厘米表示实际距离8千米，用比表示为1：800000．解答：解：8千米=800000厘米，所以此线段比例尺表示为：1：800000，它可以表示图上距离是实际距离的，也可以表示实际距离是图上距离的800000倍，也表示图上距离与实际距离的比是1：800000．所以在ABC答案中，只有B答案正确．故选：B．点评：此题考查了线段比例尺的意义．7．在比例尺是1：3000000的地图上，量得A、B两港距离为12cm，一艘货轮于上午7时出发，以每小时24km的速度从A港开向B港，到达B港的时间是（）A．22时B．23时C．21时考点：比例尺应用题．专题：压轴题；比和比例应用题．分析：先根据图上距离÷比例尺=实际距离，再根据路程÷速度=时间，进而解出答案．解答：解：12÷=36000000（厘米）=360（千米），360÷24=15（小时），上午7时过15小时是晚上的22时，故选：A．点评：此题主要考查图上距离、实际距离和比例尺的关系，以及行程问题中的基本数量关系“路程÷速度=时间”．8．在比例尺是1：30，000，000的地图上量得甲、乙两地相距5.5厘米，一辆汽车按3：2分两天行完全程，那么第二天行的路程是（）A．6.6千米B．66千米C．660千米D．6600千米考点：比例尺应用题．分析：先根据比例尺求出实际的全程，再把全程按照3：2的比例分配即可．解答：解：30000000×5.5=165000000（厘米）；165000000厘米=1650（千米）；3+2=5，1650÷5×2=660（千米）；故答案选：C．点评：本题先利用比例尺求出实际的全程，再把全程按比列分配；注意1千米=100000厘米．9．在比例尺是1：3000000的地图上，量得A、B两港距离为12厘米，一艘货轮于上午7时以每小时24千米的速度从A港开向B港，到达B港的时间是（）A．16点B．18点C．20点D．22点考点：比例尺应用题．分析：先根据图上距离÷比例尺=实际距离，再根据路程÷速度=时间，进而解出答案．解答：解：12÷=36000000（厘米）=360（千米），360÷24=15（小时），上午7时过15小时是晚上的22时，故选：D．点评：解答此题用了比例尺和行程方面的知识解答．10．一个正方形的面积是100平方厘米，把它按10：1的比放大．放大后图形的面积是多少平方厘米？（）A．1000平方厘米B．2000平方厘米C．10000平方厘米考点：比例尺应用题．分析：一个正方形的面积是100平方厘米，它的边长是10厘米，把它按10：1的比放大，就是把这个正方形的边长扩大到原来的10倍，据此可求出放大后图形的面积．解答：解：10×10=100（厘米），100×100=10000（平方厘米）；故选：C．点评：本题是考查图形的放大与缩小，图形放大与缩小的倍数是指图形边长放大与缩小的倍数．C档（跨越导练）1．在比例尺是1：1000的图纸上，量得一块正方形地的边长是5厘米，则这块地的实际面积是（）A．250000平方厘米B．2500平方厘米C．2500平方米D．250平方米考点：比例尺应用题；长方形、正方形的面积．专题：平面图形的认识与计算．分析：图上距离和比例尺已知，依据“实际距离=图上距离÷比例尺”即可求出正方形的边长的实际长度，进而利用正方形的面积公式即可求解．解答：解：5÷=5000（厘米）=50（米），50×50=2500（平方米）；答：这块地的实际面积是2500平方米．故选：C．点评：此题主要考查依据图上距离、实际距离和比例尺之间的关系解决实际问题，解答时要注意单位的换算．2．在比例尺是1：6000000的地图上，量得广州到北京的距离是30厘米，广州到北京的实际距离约是（）千米．A．1600 B．2000 C．1800考点：比例尺应用题．专题：比和比例应用题．分析：图上距离和比例尺已知，依据“实际距离=图上距离÷比例尺”即可求出广州到北京的实际距离．解答：解：30÷=180000000（厘米）=1800（千米）；答：广州到北京的实际距离是1800千米．故选：C．点评：此题主要考查图上距离、实际距离和比例尺的关系，解答时要注意单位的换算．3．地图上的线段比例尺如图，表示这副地图的数值比例尺是（）A．B．C．D．考点：比例尺应用题；长度的单位换算．分析：依据比例尺的意义，即“图上距离与实际距离的比即为比例尺”即可将线段比例尺化成数字比例尺．解答：解：由题意可知：图上1厘米代表实际60千米，又因60千米=6000000厘米，所以1厘米：6000000厘米=1：6000000；故选：C．点评：此题主要考查比例尺的意义，解答时要注意单位的换算．4．在比例尺是1：30000000的地图上，量得甲地到乙地的距离是5厘米，一辆汽车按3：2的比例分两天行完全程，两天行的路程差是（）A．300km B．600km C．900km D．1500km考点：比例尺应用题；按比例分配应用题．专题：比和比例应用题．分析：要求两天行的路程差是多少千米，先根据“图上距离÷比例尺=实际距离”，求出甲地到乙地的路程，然后根据两天行的路程比，得出第一天行了全程的第二天行了全程的，第一天比第二天多行全程的﹣，解答即可得出结论．解答：解：5÷×（﹣），=150000000×，=30000000（厘米）；30000000厘米=300千米；故选：A．点评：此题应根据图上距离、比例尺和实际距离的关系，先求出全程，进而运用按比例知识进行解答即可．5．在比例尺是1：2000000的地图上，量得两地距离是28厘米，这两地的实际距离是560千米，若一辆货车以70千米每小时的速度由贵阳往晴隆行驶，则需要8小时．考点：比例尺应用题；简单的行程问题．专题：比和比例应用题；行程问题．分析：已知比例尺和图上距离求实际距离，求出实际距离，再根据路程÷速度=时间，列式解答．解答：解：（1）28=56000000（厘米），56000000厘米=560千米，（2）560÷70=8（小时），答：这两地的实际距离是560千米，需要8小时．故答案为：560，8．点评：此题主要考查比例尺的意义及已知比例尺和图上距离求实际距离．注意单位的换算．6．在比例尺是1：10000000的地图上，量得甲地到乙地的距离是10.2厘米，一辆汽车按3：2的比例分两天跑完全程，两天跑的路程的差是204千米．考点：比例尺应用题．专题：比和比例应用题．分析：首先实际距离=图上距离÷比例尺，求出甲、乙两地之间的路程，已知一辆汽车按3：2的比例分两天跑完全程，第一天跑的路程占全程的，第二天跑的路程占全程的，然后根据一个数乘分数的意义，用乘法解答．解答：解：10.2，=10.2×10000000，=102000000（厘米），102000000厘米=1020千米，1020×（），=1020×，=204（千米），答：两天跑的路程的差是204千米．故答案为：204．点评：此题解答关键是根据图上距离和比例尺求出实际距离，再把比转化成分数，根据一个数乘分数的意义解答即可．7．树人小学新建一幢教学楼，地基是长50米、宽28米的长方形．画在图纸上，长是2.5厘米，宽是1.4厘米，这幅图的比例尺是1：2000．考点：比例尺应用题；长度的单位换算．分析：这道题是已知实际距离、图上距离，求比例尺的问题，运用图上距离：实际距离=比例尺，即可解决问题．解答：解：50米=5000厘米，2.5：5000=1：2000；答：这幅图的比例尺是1：2000．故答案为：1：2000．点评：此题主要考查比例尺、图上距离、实际距离三者之间的数量关系：比例尺=图上距离÷实际距离，灵活变形列式解决问题．8．在一副比例尺为1：4000000的地图上，量得平阳至杭州的公路长时10.5cm，两地实际相距420千米，如果一辆汽车每小时100千米的速度与上午10时40分从平阳开出，那么将在下午2时52分到达杭州．考点：比例尺应用题；简单的行程问题．专题：压轴题；比和比例应用题；行程问题．分析：（1）图上距离和实际距离已知，依据“实际距离=图上距离÷比例尺”即可求出平阳至杭州的公路的实际长度；（2）依据“路程÷速度=时间”即可求出这辆汽车需要的时间，进而求出到达的时刻．解答：解：（1）10.5÷=42000000（厘米）=420（千米）；答：两地实际相距420千米．（2）420÷100=4.2（小时）=4小时12分钟，所以10时40分+4小时12分=14时52分；答：这辆汽车将在下午2时52分到达杭州．故答案为：420、2、52．点评：此题主要考查图上距离、实际距离和比例尺的关系，以及行程问题中的基本数量关系“路程÷速度=时间”．9．在比例尺是1：60000000的地图上，量得甲乙两地的航线距离是2.5厘米，上午8时30分有一架飞机从甲地飞往乙地，上午11时到达．这架飞机平均每小时飞行600千米．考点：比例尺应用题．分析：已知比例尺和图上距离求实际距离，用图上距离÷比例尺=实际距离；上午8时30分有一架飞机从甲地飞往乙地，上午11时到达，飞行时间是2.5小时，再根据路程÷时间=速度，列式解答．解答：解：2.5÷=2.5×60000000=150000000（厘米）；150000000厘米=1500千米；1500÷2.5=600（千米/时）；答：这架飞机平均每小时飞行600千米．故答案为：600．点评：此题主要考查已知比例尺和图上距离求实际距离的方法，再根据路程、速度、时间三者之间的关系解答即可．10．在比例尺是1：60000000的地图上，量得甲乙两地的距2.5厘米，上午8点30分有一架飞机从甲地飞往乙地，上午9点45分到达，这架飞机每小时行1200千米．考点：比例尺应用题．分析：这道题是已知比例尺、图上距离，求实际距离，根据图上距离÷比例尺=实际距离列式求得实际距离，再进一步求出飞机速度，即可解答．解答：解：2.5÷=2.5×60000000=150000000（厘米），150000000厘米=1500千米，从上午8点30分到上午9点45分的时间为1.25小时，1500÷1.25=1200（千米）；答：这架飞机每小时行1200千米．故答案为：1200．点评：此题主要考查比例尺、图上距离、实际距离三者之间的数量关系：比例尺=图上距离÷实际距离，灵活变形列式解决问题．。

比例尺例1（一等奖创新教案）人教版数学六年级下册《比例尺》教案教学目标1.让学生在实践活动中体验生活中需要比例尺。

2通过观察、操作与交流，体会比例尺实际意义，了解比例尺的含义。

3运用比例尺的有关知识，通过测量、绘图、估算、计算等活动，学会解决生活中的一些实际问题。

4学生在自主探索，合作交流中，逐步形成分析问题、解决问题的能力和创新的意识，体验数学与生活的联系，培养学生用数学眼光观察生活的习惯。

学情分析这部分知识是在学生学习完正反比例及解比例后学习的，学生已经能够熟练地计算化简比，解比例。

在老师的引导下，通过动手操作，大胆设想、自主探究的方法进行学习，必要时进行合作交流。

重点难点重点：正确理解比例尺的含义，会求一幅地图的比例尺。

难点：运用比例尺的有关知识，通过测量、绘图、估算、计算等活动，体会比例尺的实际意义，学会解决生活中的一些实际问题。

教学准备多媒体课件。

教学过程一、复习上课之前我们先来热热身好吗？1厘米＝( )毫米1分米＝( )厘米1米＝( )厘米l千米＝( )厘米30米＝( )厘米300厘米＝( )米设计意图：这个环节为学生意义建构和后面的计算做好思想方法上的准备。

二、情景引入师：同学们真棒！对学过的知识掌握牢固，今天老师还给大家带来了一幅地图。

我们的祖国历史悠久，文化灿烂，地域辽阔，拥有960多万平方公里的土地。

960 多万平方公里的土地，为什么可以画在一张小小的纸上的呢？通过观察，你发现了什么？师：通过观察，你发现了什么？什么变了？什么没变？生：形状没变、大小变了。

教师指出：在现实生活当中，有时根据需要把实际物体缩小或扩大若干倍以后画到图纸上。

你能举出生活中这样的例子吗？教师展示照片设计意图：从学生已有的生活经验导入新课，有效地调动学生学习的积极性，而且在不知不觉中让学生体验到比例尺的意义。

师：同学们说得真好，如果要给我们的教室画一张平面图，它应该是什么形状的？你会画吗？生：长方形。

师：那我们来估一估它的长和宽吧（生：长大约12米，宽大约8米。