电源变换基础及应用第3章不连续导通模式DCM
- 格式:ppt
- 大小:2.82 MB
- 文档页数:8
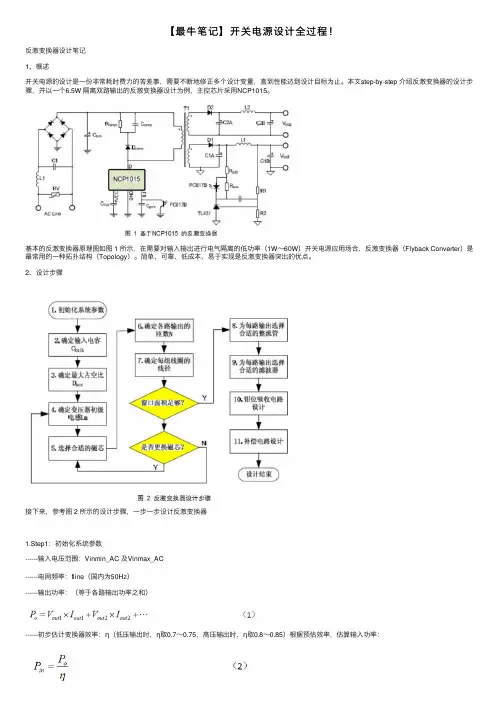
【最⽜笔记】开关电源设计全过程!反激变换器设计笔记1、概述开关电源的设计是⼀份⾮常耗时费⼒的苦差事,需要不断地修正多个设计变量,直到性能达到设计⽬标为⽌。
本⽂step-by-step 介绍反激变换器的设计步骤,并以⼀个6.5W 隔离双路输出的反激变换器设计为例,主控芯⽚采⽤NCP1015。
基本的反激变换器原理图如图 1 所⽰,在需要对输⼊输出进⾏电⽓隔离的低功率(1W~60W)开关电源应⽤场合,反激变换器(Flyback Converter)是最常⽤的⼀种拓扑结构(Topology)。
简单、可靠、低成本、易于实现是反激变换器突出的优点。
2、设计步骤接下来,参考图 2 所⽰的设计步骤,⼀步⼀步设计反激变换器1.Step1:初始化系统参数------输⼊电压范围:Vinmin_AC 及Vinmax_AC------电⽹频率:fline(国内为50Hz)------输出功率:(等于各路输出功率之和)------初步估计变换器效率:η(低压输出时,η取0.7~0.75,⾼压输出时,η取0.8~0.85)根据预估效率,估算输⼊功率:对多路输出,定义KL(n)为第n 路输出功率与输出总功率的⽐值:单路输出时,KL(n)=1.2. Step2:确定输⼊电容CbulkCbulk 的取值与输⼊功率有关,通常,对于宽输⼊电压(85~265VAC),取2~3µF/W;对窄范围输⼊电压(176~265VAC),取1µF/W 即可,电容充电占空⽐Dch ⼀般取0.2 即可。
⼀般在整流后的最⼩电压Vinmin_DC 处设计反激变换器,可由Cbulk 计算Vinmin_DC:3. Step3:确定最⼤占空⽐Dmax反激变换器有两种运⾏模式:电感电流连续模式(CCM)和电感电流断续模式(DCM)。
两种模式各有优缺点,相对⽽⾔,DCM 模式具有更好的开关特性,次级整流⼆极管零电流关断,因此不存在CCM 模式的⼆极管反向恢复的问题。
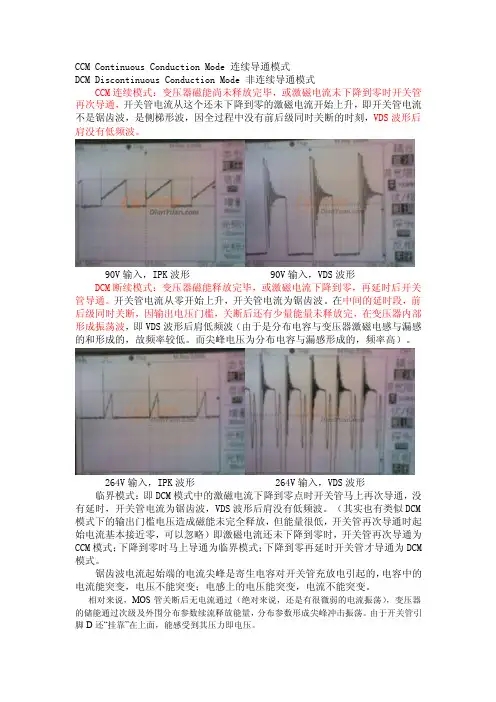
CCM Continuous Conduction Mode 连续导通模式DCM Discontinuous Conduction Mode 非连续导通模式CCM连续模式:变压器磁能尚未释放完毕,或激磁电流未下降到零时开关管再次导通,开关管电流从这个还未下降到零的激磁电流开始上升,即开关管电流不是锯齿波,是侧梯形波,因全过程中没有前后级同时关断的时刻,VDS波形后肩没有低频波。
90V输入,IPK波形 90V输入,VDS波形DCM断续模式:变压器磁能释放完毕,或激磁电流下降到零,再延时后开关管导通。
开关管电流从零开始上升,开关管电流为锯齿波。
在中间的延时段,前后级同时关断,因输出电压门槛,关断后还有少量能量未释放完,在变压器内部形成振荡波,即VDS波形后肩低频波(由于是分布电容与变压器激磁电感与漏感的和形成的,故频率较低。
而尖峰电压为分布电容与漏感形成的,频率高)。
264V输入,IPK波形 264V输入,VDS波形临界模式:即DCM模式中的激磁电流下降到零点时开关管马上再次导通,没有延时,开关管电流为锯齿波,VDS波形后肩没有低频波。
(其实也有类似DCM 模式下的输出门槛电压造成磁能未完全释放,但能量很低,开关管再次导通时起始电流基本接近零,可以忽略)即激磁电流还未下降到零时,开关管再次导通为CCM模式;下降到零时马上导通为临界模式;下降到零再延时开关管才导通为DCM 模式。
锯齿波电流起始端的电流尖峰是寄生电容对开关管充放电引起的,电容中的电流能突变,电压不能突变;电感上的电压能突变,电流不能突变。
相对来说,MOS管关断后无电流通过(绝对来说,还是有很微弱的电流振荡),变压器的储能通过次级及外围分布参数续流释放能量,分布参数形成尖峰冲击振荡。
由于开关管引脚D还“挂靠”在上面,能感受到其压力即电压。
上图电流波形上的,那个尖峰是由哪产生的,有的电流波形朝也也会有这个尖,开通瞬间的电流尖峰是次级二极管的反向恢复以及分布电容放电产生的。

例3-61 在电阻性负载三相半波可控整流电路中,如果窄脉冲出现过早,即在移到自然换相点之前,会出现什么现象?画出负载侧d u 波形。
图3-29 例3-61图解:如图3-29,当触发脉冲1g u 触发U 相晶闸管,则U 相晶闸管导通。
当1g u 触发V 相晶闸管时,这时U 相电压高于V 相电压,所以V 相晶闸管不导通,U 相晶闸管继续导通。
过了自然换相点后,尽管V 相电压高于U 相电压,但V 相晶闸管的触发脉冲2g u 消失,所以V 相晶闸管仍不通。
U 相晶闸管导通到过零点结束。
这样下去,接着导通的是W 相晶闸管。
由此可以看出,由于晶闸管间隔导通而出现了输出波形相序混乱现象,这是不允许的。
例3-62 如果图3-30a 所示电路,VT 1管无触发脉冲,试画出15α=︒、60α=︒两种情况下的d U 波形,并画出60α=︒时晶闸管VT 2两端电压2T u 波形。
图3-30 例3-62图解:VT 1管无触发脉冲,15α=︒时波形如图图3-30b 所示,其中上图打斜线部分为整流输出d u 的波形。
60α=︒时,整流输出波形如图图3-30c 上图打斜线部分所示。
VT 2晶闸管两端电压波形如图图3-30c 下图打斜线部分所示。
由图中可以看出,0~t 1区间VT 3导通,所以VT 2管承受反压U VW ,t 1~t 2区间,无晶间管导通,所以VT 2管承受正压u V ,t 3~t 4区间,晶闸管VT 2导通,两端电压为零。
t 4~t 5区间,无晶闸管导通,VT 2承受反压u V ,t 5~t 6区间,晶闸管VT 3导通,承受反向电压U VW ,t 6~t 7区间,无晶闸管导通,承受反压u V 。
例3-63 电感性负载三相桥式半控整流电路,如VT 3管无触发脉冲,试画出30α=︒,90α=︒时的d u 波形。
解:当VT 3管无触发脉冲时,凡是W 字头的线电压如WU u 、WV u 等均不导通。
30α=︒时d u 的波形如图3-31b 打斜线部分所示。

编号XXXX大学毕业设计题目高频同步整流BUCK变换器的设计与仿真毕业设计(论文)原创性声明和使用授权说明原创性声明本人郑重承诺:所呈交的毕业设计(论文),是我个人在指导教师的指导下进行的研究工作及取得的成果。
尽我所知,除文中特别加以标注和致谢的地方外,不包含其他人或组织已经发表或公布过的研究成果,也不包含我为获得及其它教育机构的学位或学历而使用过的材料。
对本研究提供过帮助和做出过贡献的个人或集体,均已在文中作了明确的说明并表示了谢意。
作者签名:日期:指导教师签名:日期:使用授权说明本人完全了解大学关于收集、保存、使用毕业设计(论文)的规定,即:按照学校要求提交毕业设计(论文)的印刷本和电子版本;学校有权保存毕业设计(论文)的印刷本和电子版,并提供目录检索与阅览服务;学校可以采用影印、缩印、数字化或其它复制手段保存论文;在不以赢利为目的前提下,学校可以公布论文的部分或全部内容。
作者签名:日期:XX大学本科毕业设计(论文)诚信承诺书本人郑重声明:所呈交的毕业设计(论文)(题目:)是本人在导师的指导下独立进行研究所取得的成果。
尽本人所知,除了毕业设计(论文)中特别加以标注引用的内容外,本毕业设计(论文)不包含任何其他个人或集体已经发表或撰写的成果作品。
作者签名:年月日(学号):高频同步整流BUCK变换器的设计与仿真摘要便携式电子产品的广泛应用,推动了开关电源技术的迅速发展。
因为开关电源具有体积小、重量轻以及功率密度和输出效率高等诸多优点,己经逐渐取代了传统的线性电源,随之成为电源芯片中的主流产品。
随着开关电源技术应用领域的扩大,对开关电源的要求也日益提高,高效率、高可靠性以及高功率密度成为趋势,这就对开关电源芯片设计提出了新的挑战。
本文首先概述了现有开关电源设计技术及其发展趋势,接着介绍了BUCK变换器的电路结构、工作原理及控制原理。
最后进行了芯片系统的仿真研究,其中首先介绍了所选芯片的性能特点及其经典电路图,然后利用LTSPICE进行了仿真验证。

反激变换器dcm模式公式推导反激变换器(flyback converter)是一种常见的开关电源拓扑结构之一,其工作原理基于电感储能和开关器件的周期性开关。
当反激变换器处于离散(DCM)模式时,输入电压和输出电压之间的关系可以通过以下公式进行推导:1. 设定以下符号和参数:- $V_{in}$:输入电压- $V_{out}$:输出电压- $D$:开关周期内开关器件导通时间比例(占空比)- $T$:开关周期- $D_{max}$:开关器件最大导通时间比例- $L$:电感器- $C$:输出电容- $N$:变压器变比- $f_s$:开关频率- $V_c$:电容器电压(很小时,近似等于$V_{out}$)- $i_L$:电感器电流2. 离散(DCM)模式下,开关周期分为两个阶段:- Tonic(升压)阶段:开关器件导通,电感器储能- Fly(负载释放)阶段:开关器件关断,电感器释放能量给负载3. 在Tonic阶段,电感器电流的变化率为:$\frac{di_L}{dt} = \frac{V_{in} - V_c}{L}$4. 在Fly阶段,电感器电流的变化率为:$\frac{di_L}{dt} = \frac{-V_c}{L}$5. 因为电感器电流在升压阶段和负载释放阶段之间变化,所以我们可以将Tonic阶段中的电流变化时间分为两个阶段:- $t_{on,1}$:电压从0到$V_c$的时间- $t_{on,2}$:电压从$V_c$下降到0的时间6. 根据电感器电流变化率的方程,我们可以得到:$\frac{di_L}{dt}=\begin{cases}\frac{V_{in}-V_c}{L},&0\leq t\leq t_{on,1}\\\frac{-V_c}{L},&t_{on,1}\leq t \leq (t_{on,1}+t_{on,2})\\\end{cases}$7. 针对两个阶段的电流变化率方程,我们可以对其进行积分得到电感器电流的表达式:$i_L(t)=\begin{cases}\frac{V_{in}}{L}t,&0\leq t \leq t_{on,1} \\\frac{V_{in}}{L}t_{on,1} -\frac{V_c}{L}(t-t_{on,1}),&t_{on,1}\leq t\leq (t_{on,1}+t_{on,2}) \\\end{cases}$8. 在Fly阶段的t时刻,电感器电流$i_L(t)$降为0,因此:$\frac{V_{in}}{L}t_{on,1} - \frac{V_c}{L}(t_{on,1}+t_{on,2}) = 0$推导得到:$t_{on,1} = \frac{V_c}{V_{in}}(t_{on,1}+t_{on,2})$9. 在Tonic阶段的电感器电能变化为:$E_{L,1} = \frac{1}{2}L(i_L(t_{on,1})^2 - 0^2) = \frac{1}{2}L(\frac{V_{in}}{L}t_{on,1})^2 =\frac{1}{2}\frac{V_{in}^2}{L}t_{on,1}^2$10. 在Fly阶段的电感器电能变化为:$E_{L,2} = \frac{1}{2}L(0^2 - (-\frac{V_c}{L}(t_{on,1}+t_{on,2}))^2 =\frac{1}{2}\frac{V_c^2}{L}(t_{on,1}+t_{on,2})^2$11. 根据能量守恒的原理,Tonic阶段的能量改变和Fly阶段的能量改变之和应等于0:$E_{L,1} + E_{L,2} = \frac{1}{2}\frac{V_{in}^2}{L}t_{on,1}^2 +\frac{1}{2}\frac{V_c^2}{L}(t_{on,1}+t_{on,2})^2 = 0$12. 根据上述能量守恒的方程,我们可以解出$t_{on,1}$和$t_{on,2}$的关系:$(V_{in}^2)t_{on,1}^2 + (V_c^2 + 2V_{in}V_c)t_{on,1}t_{on,2} + (V_c^2)t_{on,2}^2 = 0$13. 这是关于未知数$t_{on,1}$和$t_{on,2}$的二次方程,可以使用求根公式求解。

电源变换基础及应用
《电源变换基础及应用》是一门涉及电力电子技术的学科,主要研究电源的转换和控制。
这门学科的基础包括电路理论、电子学、控制理论等,应用领域非常广泛,包括电力系统、通信系统、计算机系统、工业控制等。
在电源变换基础方面,学生需要学习电源的基本概念、电路拓扑、控制方法等。
其中,电路拓扑是指电源变换电路的结构形式,例如 Buck、Boost、Buck-Boost 等;控制方法则包括脉宽调制(PWM)、脉频调制(PFM)等。
在应用方面,学生需要学习如何设计和实现各种电源变换电路,例如 DC-DC 变换器、AC-DC 变换器、DC-AC 逆变器等。
此外,还需要学习如何应用电源变换技术来解决实际问题,例如提高电源效率、减小电源体积、提高电源稳定性等。
总之,《电源变换基础及应用》是一门非常实用的学科,对于从事电子工程、电力工程、通信工程等领域的工程师和研究人员来说,具有非常重要的意义。
![033-电源设计培训【DC-DC】资料[文字可编辑]](https://uimg.taocdn.com/07035e28b84ae45c3b358c59.webp)


开关变换器和开关电源电源有如人体的心脏,是所有电设备的动力。
标志电源特性的参数有功率、电压、频率、噪声及带负载时参数的变化等;在同一参数要求下,又有体积、重量、形态、效率、可靠性等指标。
在有些情况下,一般电力要经过转换才能符合使用的需要。
例如,交流转换成直流,高电压变成低电压等。
按电力电子的习惯称谓,AC-DC(理解成AC转换成DC,其中AC表示交流电,DC表示直流电)称为整流(包括整流及离线式变换),DC-AC称为逆变,AC-AC称为交流-交流直接变频(同时也可以是变压),DC-DC称为直流-直流变换。
为达到转换目的,手段是多样的。
20世纪60年代前,研发了半导体器件,并以次器件为主实现这些转换。
电力电子学科从此形成并有了近30年的迅速发展。
所以,广义地说,凡半导体功率器件作为开关,将一种电源形态转变成为另一形态的主电路都叫做开关变换器电路;转变时用自动控制闭环稳定输出并有保护环节则称开关电源(Switching Power Supply)。
开关电源主要组成部分是DC-DC变换器,因为它是转换的核心,涉及频率变换。
目前DC-DC变换中所用的频率提高最快,它在提高频率中碰到的开关过程、损失机制,为提高效率而采用的方法,也可作为其他转换方法参考。
常见到离线式开关变换器(Off-line Switching Converter)名称,即AC-DC变换,也常称开关整流器;它不仅包含整流,而且整流后又做了DC-DC变换。
所谓离线并不是变换器与市电线路无关的意思,只是变换器中因有高频变压器隔离,使输出的直流与市电隔离,所以称离线式开关变换器。
稳压电源的分类及基本知识开关型交流稳压电源它应用于高频脉宽调制技术,与一般开关电源的区别是它的输出量必须是与输入侧同上频、同相的交流电压。
它的输出电压波型有准方波、梯型波、正弦波等,市场上的不间断电源(UPS)抽掉其中的蓄电源和充电器,就是一台开关型交流稳压电源的稳压性好,控制功能强,易于实现智能化,是非常具有前途的交流稳压电源。
buck电路不连续导通状态的时间常数摘要:1.BUCK电路基本概念与原理2.不连续导通状态的原因3.时间常数的影响因素4.应对不连续导通状态的方法5.总结与建议正文:buck电路是一种常见的降压型DC-DC变换器,其工作原理是通过在输入端开关控制导通与截止,使电能转化为电压较低的直流电源。
在buck电路中,PMOS管和NMOS管交替工作,实现电能的传递和电压的降低。
然而,在实际应用中,buck电路的PMOS管有时会出现一直处于导通状态的现象。
这种情况通常是由于不连续导通状态(Discontinuous Conduction Mode,简称DCM)引起的。
DCM是指在buck电路的工作过程中,由于电感电流的不连续性,导致PMOS管在某些时间段内一直处于导通状态。
不连续导通状态的出现主要受到以下几个因素的影响:1.占空比:占空比是开关导通时间与周期的比值,当占空比大于0.5时,电感电流不能连续流过,从而导致DCM。
2.电感值:电感值越大,电感电流变化的速率越慢,容易产生不连续导通状态。
3.负载电流:负载电流越大,电感电流的变化幅度越大,不连续导通的可能性越高。
针对不连续导通状态,可以采取以下方法进行优化:1.调整占空比:通过改变占空比,可以控制电感电流的连续性,从而减小DCM的影响。
2.选择合适的电感值:电感值的大小直接影响到电感电流的变化速率,选择合适的电感值可以降低DCM出现的概率。
3.增加缓冲电路:在buck电路中增加缓冲电路,可以提高电路的稳定性,减少DCM的影响。
4.优化控制策略:通过调整开关控制策略,例如使用滞环控制或PWM控制,可以有效降低DCM的发生。
总之,不连续导通状态在buck电路中是一个常见问题,需要从多个方面进行分析和解决。
在实际应用中,我们要充分考虑电路参数的匹配、控制策略的优化,以提高buck电路的稳定性和可靠性。
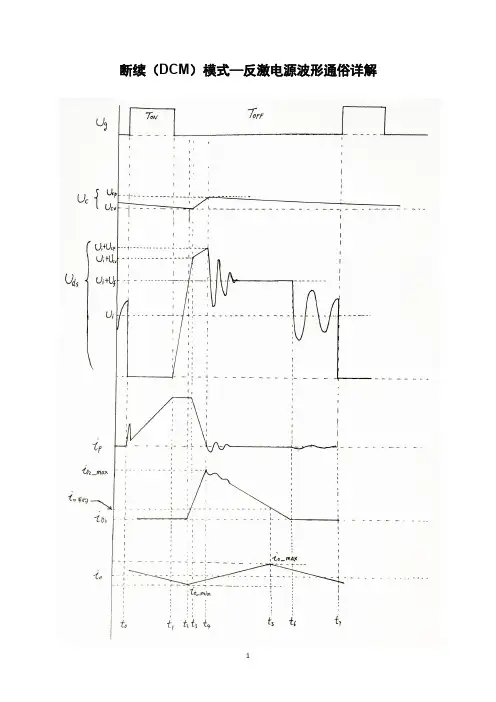
反激变换器不连续模式的特征反激变换器是一种常见的电源转换器,其工作方式可以分为连续导通模式和不连续导通模式。
本文将重点介绍反激变换器的不连续模式特征以及相关的应用和调试指导。
不连续模式指的是在工作周期中,反激变换器的辅助开关管(例如二极管或MOSFET)在某些时候不会导通,因而导致电流波形非连续。
首先,不连续模式的特征之一是辅助开关管在每个工作周期开始时都会关闭。
这是由于输入电压的极性和电感元件的磁场极性导致的。
这种不连续导通现象不同于连续导通模式,需要在设计过程中特别注意。
其次,不连续模式下反激变换器的输出电流波形通常为脉冲状。
这是因为当辅助开关管关闭时,电感元件上的电流不能连续流过负载。
相比之下,连续导通模式下的输出电流波形更接近直流。
此外,不连续模式也可能导致电压尖峰或电流尖峰的产生。
辅助开关管在每个工作周期中关闭时,电感元件上的能量无法即时耗尽,从而产生尖峰现象。
这些尖峰可能会对系统的稳定性和效率产生不利影响,因此需要采取适当的措施来抑制。
当然,不连续模式也可以在一些特定应用中被有意利用。
例如,在一些低功率应用中,通过精心设计反激变换器的参数和元件选择,可以实现高效率的转换,并有效降低系统成本和尺寸。
对于调试反激变换器的不连续模式,以下几点需要特别注意。
首先,需要确保开关频率和元件的电压和电流承受能力匹配。
不连续模式会导致辅助开关管承受较高的电压和电流,因此在选用元件时要特别关注这些参数。
其次,需要注意反激变换器的控制策略,特别是在不连续模式下的控制信号生成。
精确的控制可以提高系统的稳定性和效率,避免不必要的能量损耗和不稳定的波形。
最后,充分了解不连续模式的特征并进行合理的设计和调试,可以有效提高反激变换器的性能和可靠性。
通过深入研究不连续模式的工作原理和特性,我们可以充分利用其优势,为各种电源转换应用提供更稳定、高效的解决方案。
总之,反激变换器的不连续模式具有特殊的特征,并且在不同的应用中会有不同的影响和利用方式。