同济大学理论力学模拟题A
- 格式:pdf
- 大小:150.20 KB
- 文档页数:4

同济大学课程考核试卷(A 卷) 2006—2007学年第一学期命题教师签名:审核教师签名: 课号:课名:工程力学考试考查:此卷选为:期中考试()、期终考试()、重考()试卷 年级专业学号姓名得分=10m/s 2,成60度mm 计)2_;计的刚当无初B 的12C5均质细杆AB 重P ,长L ,置于水平位置,若在绳BC 突然剪断瞬时有角加速度?,则杆上各点惯性力的合力的大小为_gPL 2α,(铅直向上)_,作用点的位置在离A 端_32L_处,并在图中画出该惯性力。
6铅垂悬挂的质量--弹簧系统,其质量为m ,弹簧刚度系数为k ,若坐标原点分别取在弹簧静伸长处和未伸长处,则质点的运动微分方程可分别写成_0=+kx x m _和_mg kx x m =+ _。
二、计算题(10分)图示系统中,曲柄OA 以匀角速度?绕O 轴转动,通过滑块A 带动半圆形滑道BC 作铅垂平动。
已知:OA?=?r?=?10?cm ,??=?1?rad/s ,R?=?20?cm 。
试求??=?60°时杆BC 的加速度。
解:动点:滑块A ,动系:滑道BC ,牵连平动 由正弦定理得: 34.34=βcm/s 55.566.115sin 2r =︒=AA v v [5分]向ζ方向投影:2cm/s 45.7=[10分]三、计算题(15分)图示半径为R 的绕线轮沿固定水平直线轨道作纯滚动,杆端点D 沿轨道滑动。
已知:轮轴半径为r ,杆CD 长为4R ,线段AB 保持水平。
在图示位置时,线端A 的速度为v ,加速度为a,铰链C 处于最高位置。
试求该瞬时杆端点D 的速度和加速度。
解: 轮C 平面运动,速度瞬心P 点CO [8分](1) 物块下落距离时轮中心的速度与加速度; (2) 绳子AD段的张力。
解:研究系统:T 2-T 1=ΣW i223C v m +21J C ω2+21J B ω2+221A vm =m 1gs [5分] 式中:2321r m J C =,22ρm J B =代入得:v C =23222113222r m ρm R m gsm r++[7分]式两边对t 求导得:a C =23222113222r m ρm R m grRm ++[10分]对物A:m a=ΣF ,即:m 1a A =m 1g -F AD F AD =m 1g -m 1a A =m 1g -ra R m C⋅1[15分][15六、计算题(15分)在图示系统中,已知:匀质圆柱A 的质量为m1,半径为r ,物块B 质量为m 2,光滑斜面的倾角为?,滑车质量忽略不计,并假设斜绳段平行斜面。

理论力学A 卷参考答案一、选择题1-6 DABADC二、填空题(1) 绝对速度 相对速度 牵连速度(2) 平动 转动 (3) 1442222=+b y b x ,2bk ,2bk 2 (4) l M2,l M(5) 2p ml ω=,(→); 2(65/24)o L m l ω=,逆时针方向(6) mL ω/2,mL 2ω/3,mL 2ω2/6三、计算题1、解:(1)设圆柱O 有向下滚动趋势,取圆柱O0=∑A M ----0sin max 1T =-⋅-⋅M R F R θP0=∑y F ----0cos N =-θP F又N max F M δ= ……………………2分设圆柱O 有向上滚动趋势,取圆柱O0=∑A M ----0sin max 2T =+⋅-⋅M R F R θP0=∑y F ----0cos N =-θP F ……………………2分又N max F M δ=……………………2分系统平衡时: ……………………2分)cos (sin 1T θR θP F δ-=(2)设圆柱O 有向下滚动趋势.0=∑C M 0m a x =-⋅M R F s0=∑y F 0c o s N =-θP F 又θδcos P R F s = 所以θδcos P R F s = (2)只滚不滑时,应有 θP f F f F s s s cos N =≤ R f s δ≥同理,圆柱O 有向上滚动趋势时得 R f s δ≥只滚不滑时,Rf s δ≥ (2)2、解:速度分析:1. 杆AB 作平面运动,基点为B.……………………….1分2.动点 :滑块 A ,动系 :OC 杆……………………….2分 沿v B 方向投影:……………………….1分……………………….1分 沿vr 方向投影:……………………….1分加速度分析:n t ABAB B A a a a a ++=……………………….2分 沿v C 方向投影:……………………….2分……………………….1分……………………….1分3、 解:突然解除约束瞬时,杆OA 将绕O 轴转动,不再是静力学问题。
同济大学课程考核试卷(A 卷) 2012 — 2013学年 第二学期命题教师签名: 审核教师签名:课号:125003 课名:理论力学 考试/考查:考试此卷选为:期中考试( )、期终考试( √ )、重考( )试卷年级 专业 学号 姓名 得分题号 一 二 三 四 五 六总分 题分 30分 15分 15分 15分 10分 15分 100分 得分一.填空题(每小题5分,共30分)1.已知力F 与尺寸a 。
则力F 在y 轴上的 投影为______________、力F 对x 、z 轴的矩 为_________________、_________________。
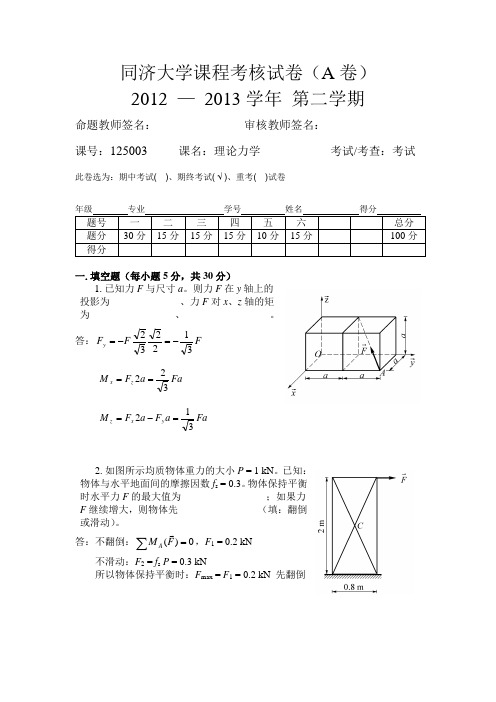
答:F FF y 312232-=-= Fa a F M z x 322== Fa a F a F M y x z 312=-=2.如图所示均质物体重力的大小P = 1 kN 。
已知: 物体与水平地面间的摩擦因数f s = 0.3。
物体保持平衡 时水平力F 的最大值为_________________;如果力 F 继续增大,则物体先________________(填:翻倒 或滑动)。
答:不翻倒:∑=0)(F M A,F 1 = 0.2 kN不滑动:F 2 = f s P = 0.3 kN所以物体保持平衡时:F max = F 1 = 0.2 kN 先翻倒3.半径为r 的车轮沿固定圆弧面作纯滚 动,若某瞬时轮子的角速度为ω、角加速度 为α,则轮心O 的切向加速度和法向加速度 的大小分别为________________________。
答:αr a o=t ,rR r r R v a o+=+=2220n ω。
4.直角弯管OAB 在平面内以匀角速度ω=2rad/s 绕 O 转动,动点M 以相对速度v r =20mm/s 沿弯管运动。
若动坐标系在弯管上,则图示瞬时动点的牵连加速度 a e =______________、科氏加速度a C =____________。

密封线 第二学期理论力学(A)试卷1. 立方体的C 点作用一力F ,已知F =800N 。
则力F 在坐标轴x 、y 、z 上的投影为:Fz = ; ; ; 。
2. 悬臂梁受载荷集度的均布力 和矩M=2kN·m 的力偶作用,如图所示, 则该力系向A 点简化的结果为:__________,RX F = __________,RY F =__________A M =。
3. 如图所示平面机构中,AB 杆的A 端靠在光滑墙上,B 端铰接在滑块上,若选AB 上的A 为动点,滑块为动系,则A 的相对运动为 。
4. 杆AB 作平面运动,已知某瞬时B 点的 速度大小为=6m/s ,方向如图所示,则在该瞬时A 点的速度最小值为min _________V =。
二、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题3分,共21分)5. 如果力R F是1F、2F二力的合力,用矢量方程表示为R F=1F+2F,则三力大小之间的关系为()。
A. 必有R F=1F+2F;B. 不可能有R F=1F+2F;C. 必有R F>1F,R F>2F;D. 可能有R F<1F,R F<2F。
6. 正立方体的前侧面沿AB方向作用一力F,则该力()。
A. 对轴之矩全相等;B. 对三轴之矩全不相等;C. 对轴之矩相等;D. 对轴之矩相等。
7. 点作曲线运动时,“匀变速运动”指的是()。
A. =常矢量;B. =常量;C. =常矢量;D. =常量。
8. 刚体绕定轴转动,()。
A. 当转角时,角速度为正;B. 当角速度时,角加速度为正;C. 当与同号时为加速转动,当与异号时为减速转动;D. 当α时为加速转动,当α时为减速转动。
9. 平面运动刚体相对其上任意两点的()。
A. 角速度相等,角加速度相等;B. 角速度相等,角加速度不相等;C. 角速度不相等,角加速度相等;D. 角速度不相等,角加速度不相等。

《理论力学》考试试卷(答案)1.如图3所示,a图中B端的反支力为M/2L , b图中B端的反支力为M/L 。
2.某桁架如图2所示,其中零杆数目为—o3.如图3所示,刚架受到一对力偶和一对共线的力作用,且知m=5kN.m以及P = 41kN , A处支座反力分别为X.= 0 ,Y A= 0 ,此= (逆时针为正)。
5.如图4所示,刚体作平面运动,其平面图形(未画出)内两点A、B相距L = 3m, 两点的加速度均垂直于AB连线,方向相反,大小分别为5m/s和10m/s。
则该瞬时图形的角速度的大小为5 rad/s 。
6.如图5所示,均质直杆0A质量为m,长为L,以角速度3绕固定轴0顺时针转动(逆时针为正)。
在图示位置直杆水平,其动量的大小为mLco/2 ;直杆对0轴动量矩的大小为ml? 3/3 ,杆动能大小为ml; 3 76。
二、计算题(共60分)。
1.如图所示,梁AC用三根链杆支承,梁受集中力P和均布荷载作用,已知P=40kN, q=5kN/m,试求各链杆的内力。
(本题15分)解:受力分析如图所示:2.桁架如图所示,试求杆件CD, CE和EF的内力。
(本题15分)解:由图分析可知CD杆为0杆。
……(1分)1)先取整体分析,如图所示分别对A点和B点取矩:Am尸)=o-2x10-4x10-6x10-8x5 + 8x7? = 0D2>*)=°2x10 + 4x10 + 6x10 + 8x5-8x7?^ =0解得:R A =20kN, R B =20kN如图取I - I截面左半部分对A点取矩,取II-11截面右部分对B点取矩£ 〃很了)= 0-2xl0-2x S CE sin(cif)-lx S CE cos(o) = 0£ 〃七(了)= o8X7?A +8X5+6X10+4X10+6X S CE sin(。
)-lx S CE cos(。
)+ 4x S FE = 0上式解得:S^=—11.18KN, S FF = 1QKNCc r Zi3,图示机构中,曲柄04长为r,绕。
《理论力学》期末考试卷模拟试卷01一.判断题(认为正确的请在每题括号内打√,否则打×;每小题3分,共15分)(√)1.几何约束必定是完整约束,但完整约束未必是几何约束。
(×)2.刚体做偏心定轴匀速转动时,惯性力为零。
(×)3.当圆轮沿固定面做纯滚动时,滑动摩擦力和动滑动摩擦力均做功。
(√)4.质点系动量对时间的导数等于作用在质点系上所有外力的矢量和。
(√)5.平面运动随基点平动的运动规律与基点的选择有关,而绕基点转动的规律与基点选取无关。
二.选择题(把正确答案的序号填入括号内,每小题3分,共30分)1.如图1所示,楔形块A,B自重不计,并在光滑的mm,nn 平面相接触。
若其上分别作用有大小相等,方向相反,作用线相同的二力P,P’,则此二刚体的平衡情况是( A )(A)二物体都不平衡(B)二物体都能平衡(C)A平衡,B不平衡(D)B平衡,A不平衡2.如图2所示,力F作用线在OABC平面内,则力F对空间直角坐标Ox,Oy,Oz轴之距,正确的是( C )(A)m x(F)=0,其余不为零(B)m y(F)=0,其余不为零(C)m z(F)=0,其余不为零(D)m x(F)=0, m y(F)=0, m z(F)=03.图3所示的圆半径为R,绕过点O的中心轴作定轴转动,其角速度为ω,角加速度为ε。
记同一半径上的两点A,B的加速度分别为a A,a B(OA=R,OB=R/2),它们与半径的夹角分别为α,β。
则a A,a B的大小关系,α,β的大小关系,正确的是(B )(A)BAaa2=, α=2β(B)BAaa2=, α=β(C)BAaa=, α=2β(D)BAaa=, α=βy图14.直管AB 以匀角速度ω绕过点O 且垂直于管子轴线的定轴转动,小球M 在管子内相对于管子以匀速度v r 运动。
在图4所示瞬时,小球M 正好经过轴O 点,则在此瞬时小球M 的绝对速度v ,绝对加速度a 是(D )(A )v=0,a =0 (B )v=v r, a =0 (C )v=0,r v a ω2=,← (D )v=v r , r v a ω2=,← 5. 图5所示匀质圆盘质量为m ,半径为R ,可绕轮缘上垂直于盘面的轴转动,转动角速度为ω,则圆盘在图示瞬时的动量是( B ) (A )K=0 (B )K=mR ω,↓ (C )K=2mR ω ,↓ (D )K=mR ω2 ,←6. 条件同前题(5),则圆盘的动能是(D )(A )2221ωmR T = (B )2241ωmR T =(C )22ωmR T = (D )2243ωmR T =7. 匀质半圆盘质量为m ,半径为R ,绕过圆心O 并垂直于盘面的定轴转动(图6),其角速度为ω,则半圆盘对点O 的动量矩的大小L 0 是( C )。
一、判断题 (正确打“√”,错误打“×”,每小题2分,共10分)1、平面任意力系,只要主矢0≠'RF,最后必可简化为一合力。
( √ )2、刚体在3个力的作用下平衡,这3个力不一定在同一个平面内。
( × )3、某刚体作平面运动时,若A 和B 是其平面图形上的任意两点,则速度投影定理[][]AB B AB A v v=恒成立。
( √ )4、作瞬时平移的刚体,该瞬时其惯性力系向质心简化,主矩为零。
( × )5、当牵连运动为定轴转动时一定有科氏加速度。
( × )二、选择题(每一小题只有一个正确答案,多选不给分。
请将正确答案的序号填入括号内。
每题3分,共15分)1、已知杆AB 和CD 的自重不计,且在C 处光滑接触。
若作用在AB 杆上的力偶矩为1m ,欲使系统保持平衡,需在CD 杆上施加力偶矩2m ,其大小为( A )。
A 、 12m m =;B 、 1234m m =;C 、 122m m =;D 、 1221m m =。
2、平面一般力系的二力矩式平衡方程为,0)(,0==∑∑i A y F M F 0)(=∑i B F M ,其适用条件是 ( D )。
A 、 A 、B 两点均在y 轴上; B 、 y 轴垂直于 A 、B 连线;C 、 x 轴垂直于A 、B 连线;D 、 y 轴不垂直于A 、B 连线。
3、圆盘作定轴转动,若某瞬时其边缘上A 、B 、C 、D 四点的速度、加速度如图所示,则( D )的运动是可能的。
(A )点A 、B ; (B )点A 、C ; (C )点C 、B ;Am 1BCD m 260ºAD C B V 1V 2V 3V 4a 2a 1a 4a 3O(D )点C 、D 。
4、平面图形上任意两点A 、B 的加速度A a 、B a 与A 、B 连线垂直,且B A a a ≠,则该瞬时平面图形的角速度ω和角加速度α为 ( C )。
理论力学AI(或B)期末考试模拟试题一、 选择题(多选或单选,在正确答案上打√。
每题2分共10分)1、正方体上的六个面各作用有一个平面汇交力系,则该力系独立的平衡方程最多有:A:4个;B:6;C:8个;D:12个2、若质点的速度矢量(不为零)与加速度矢量(不为零)始终垂直,则质点可能作:A:直线运动;B:平面曲线运动;C:空间曲线运动3、结构如图1所示,力F与杆1和杆2平行,不计各构件自重,则图示结构中的零力杆为:A:1杆;B:2杆;C:3杆图1 图24、平面运动刚体上三个点A、B、C构成等边三角形,某瞬时各点加速度或速度矢量如图2所示。
则图2中所示的运动是可能的。
A:图2(a);B: 图2(b);C: 图2 (a)和(b)5、质心在转轴上的匀角速度定轴转动刚体,其惯性力系向转轴上的某点简化的结果可能是:A:零力系;B:一个力偶;C:一个力;D:一个力螺旋二、 填空题(将正确答案的最简结果填在空格内,每空5分,共50分)1、平面桁架如图3所示,该桁架是(选择:静定桁架或静不定F=(拉力为正)。
桁架)。
杆件2的内力2图3 图 42、结构及其受力如图4所示,已知均布载荷集度N/m 10=q ,力偶矩的大小,,不计结构自重。
则CD 杆上C 端所受的约束力的大小为F = m N 5⋅=M m 1=a N 。
3、系统如图5所示,杆重为W ,半径为R 的均质圆盘重为2W ,杆与水平线的夹角为,OC 铅垂,不计铰链处的摩擦。
无论水平弹簧的拉力有多大,系统都能在图示位置实现自锁。
则杆与圆盘间的最小静滑动摩擦因数1O A 045=θ=min f 。
图 图65 4、四根杆件用铰链连接如图6所示,在水平杆AB 上作用有一力偶矩为M 的力偶,不计构建自重,则系统平衡时,铅垂杆AC 的内力=F (拉力为正)。
5、质量为m 的质点M 在OA 管内运动,OA 管绕水平轴O 在铅垂面内运动,管子与质点M 间的动滑动摩擦因数为。