理论力学分析讨论课——静力学部分实例讲解 [同济大学]
- 格式:pdf
- 大小:1.31 MB
- 文档页数:12


第一章静力学【竞赛知识要点】重心共点力作用下物体的平衡物体平衡的种类力矩刚体的平衡流体静力学(静止流体中的压强)【内容讲解】一.物体的重心1.常见物体的重心:质量均匀分布的三角板的重心在其三条中线的交点;质量均匀分布的半径R的半球体的重心在其对称轴上距球心3R/8处;质量均匀分布的高为h的圆锥体的重心在其对称轴上距顶点为3h/4处。
2.重心:在xyz 三维坐标系中,将质量为m的物体划分为质点m1、m2、m3……m n.设重心坐标为(x0,y0,z0),各质点坐标为(x1,y1,z1),(x2,y2,z2)……(x n,y n,z n).那么:mx0=∑m i x i my0=∑m i y i mz0=∑m i z i【例题】1、(1)有一质量均匀分布、厚度均匀的直角三角板ABC,∠A=30°∠B=90°,该三角板水平放置,被A、B、C三点下方的三个支点支撑着,三角板静止时,A、B、C三点受的支持力各是N A、N B、N C,则三力的大小关系是.(2)半径为R的均匀球体,球心为O点,今在此球内挖去一半径为0.5R的小球,且小球恰与大球面内切,则挖去小球后的剩余部分的重心距O点距离为.2、如图所示,质量分布均匀、厚度均匀的梯形板ABCD,CD=2AB,求该梯形的重心位置。
3、在质量分布均匀、厚度均匀的等腰直角三角形ABC(角C为直角)上,切去一等腰三角形APB,如图所示。
如果剩余部分的重心恰在P点,试证明:△APB的腰长与底边长的比为5:4.4、(1)质量分别为m,2m,3m……nm的一系列小球(可视为质点),用长均为L的细绳相连,并用长也是L的细绳悬于天花板上,如图所示。
求总重心的位置5、如图所示,质量均匀分布的三根细杆围成三角形ABC,试用作图法作出其重心的位置。
6、如图所示,半径为R圆心角为θ的一段质量均匀分布的圆弧,求其重心位置。
7、论证质量均匀分布的三角形板的重心在三条中线的交点上8、求半径为R的厚薄均匀的半圆形薄板的重心9、均匀半球体的重心问题10、均匀圆锥体的重心11、如图所示,有一固定的半径为R 的光滑半球体,将一长度恰好等于R 21、质量为m 的均匀链条搭在球体上,其一端恰在球体的顶点上,并用水平拉力拉住链条使之静止,求拉力的大小。

静力学问题解析静力学是力学的一个重要分支,研究物体在静止状态下的受力和平衡条件。
在实际生活和工程实践中,静力学问题的解析具有重要意义。
本文将从静力学概念、平衡条件和静力学应用等方面进行阐述,并通过具体示例来说明。
一、静力学概念静力学是研究物体在静止状态下的受力和平衡条件的学科。
它假设物体处于平面上,不考虑物体的形变和运动,只关注物体受到的力和力的平衡条件。
物体受力主要有重力、支持力、摩擦力等。
重力是所有物体都具有的,它的方向始终指向地心。
支持力是物体受到支撑平面的力,与物体与支撑平面的角度有关。
摩擦力是物体与支撑平面接触面之间的摩擦产生的力,与物体受到的外力和摩擦系数有关。
二、平衡条件物体在静止状态下必须满足平衡条件才能保持稳定。
平衡条件有两个:力的平衡和力矩的平衡。
1.力的平衡:物体受到的合力为零,即所有受力的矢量和为零。
当物体受到多个力时,通过向量相加来求解合力。
合力为零时,物体处于力的平衡状态。
举个例子来说明。
假设一个木块放在水平支撑平面上,受到重力和支持力的作用。
重力向下,支持力向上,它们大小相等,方向相反,合力为零。
这样木块就能在平面上保持静止。
2.力矩的平衡:物体受到的合力矩为零,即所有受力产生的力矩的矢量和为零。
力矩是力对物体产生的转动效应,它的大小等于力的大小与力臂的乘积。
力臂是力作用点到旋转轴的距离。
继续上面的例子,如果我们在木块上施加一个水平向右的力,这个力就会产生一个与支撑平面垂直的力矩。
为了使木块保持平衡,其余力必须产生一个与之相等大小但方向相反的力矩,以达到力矩平衡。
三、静力学应用静力学的应用非常广泛,不仅在日常生活中,也在工程实践中起着重要的作用。
1.静力学在桥梁的设计和建造中有着重要地位。
桥梁作为承载人车等载荷的结构,必须满足力的平衡和力矩平衡的条件,以确保桥梁的稳定性和安全性。
2.静力学也在建筑物的设计和施工中发挥着重要的作用。
例如,大楼的地基必须能够承受建筑物的重力,支撑力的大小和方向也需要经过精确计算和合理设计。
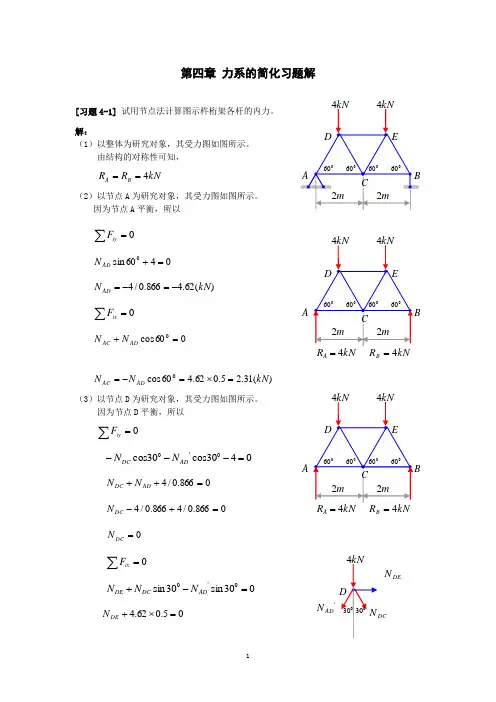
第四章 力系的简化习题解[习题4-1] 试用节点法计算图示杵桁架各杆的内力。
解:(1)以整体为研究对象,其受力图如图所示。
由结构的对称性可知, kN R R B A 4==(2)以节点A 为研究对象,其受力图如图所示。
因为节点A 平衡,所以0=∑iyF0460sin 0=+AD N)(62.4866.0/4kN N AD -=-=0=∑ixF060cos 0=+AD AC N N)(31.25.062.460cos 0kN N N AD AC =⨯=-= (3)以节点D 为研究对象,其受力图如图所示。
因为节点D 平衡,所以 0=∑iyF0430cos 30cos 0'0=---AD D C N N 0866.0/4=++AD D C N N 0866.0/4866.0/4=+-D C N0=DC N0=∑ixF030sin 30sin 0'0=-+AD D C D E N N N 05.062.4=⨯+DE NkN4)(akN4AB RkN 2AC23N A )(31.2kN N DE -=(4)根据对称性可写出其它杆件的内力如图所示。
[习题4-2] 用截面法求图示桁架指定杆件 的内力。
解:(a)(1)求支座反力以整体为研究对象,其受力图如图所示。
由对称性可知,kN R R B A 12==(2)截取左半部分为研究对象,其受力图 如图所示。
因为左半部分平衡,所以0)(=∑i CF M0612422843=⨯-⨯+⨯+⨯N 063243=⨯-++N )(123kN N =kN2AC23N A0=∑ixF0cos cos 321=++N N N αθ01252252421=+⋅+⋅N N012515221=+⋅+⋅N N0512221=++N N ……..(1) 0=∑iyF02812sin sin 21=--++αθN N025*******=+⋅+⋅N N02525121=+⋅+⋅N N052221=++N N0544221=++N N ……..(2) 05832=-N)(963.53/582kN N ==)(399.1652963.5252221kN N N -=-⨯-=--=解:(b )截取上半部分为研究对象,其受力图如图所示。


工程力学中的静力学分析在工程领域中,静力学分析是一项至关重要的研究内容,它为设计安全可靠的结构和机械系统提供了坚实的理论基础。
静力学主要关注物体在静止状态下的受力情况,通过对力的平衡条件的分析,我们能够预测物体的稳定性、结构的承载能力以及机械部件之间的相互作用。
静力学的基本概念包括力、力偶、力矩等。
力是一个有大小和方向的矢量,它可以使物体产生运动或变形。
力偶则是由两个大小相等、方向相反且不共线的力组成,力偶只能使物体产生转动效果。
力矩是力对某一点的转动效应,等于力乘以力臂。
理解这些基本概念是进行静力学分析的第一步。
在实际工程问题中,我们经常需要对物体进行受力分析。
这意味着要确定作用在物体上的所有力,包括主动力和约束力。
主动力是已知的、能够使物体运动或有运动趋势的力,例如重力、驱动力等。
约束力则是由物体与周围环境的相互作用产生的,限制了物体的运动,常见的约束力有支持力、摩擦力等。
为了清晰地表示物体的受力情况,我们通常绘制受力图,将物体从其所处的系统中隔离出来,画出所有作用在它上面的力。
力的平衡条件是静力学分析的核心。
对于一个处于平衡状态的物体,其受到的所有力的矢量和必须为零,同时对任意一点的力矩之和也必须为零。
这两个条件可以用数学表达式表示为:∑F = 0 和∑M = 0。
通过建立和求解这些平衡方程,我们可以确定未知的力或力偶的大小和方向。
例如,在一个简单的悬臂梁结构中,已知梁的长度、所承受的集中载荷以及支座的类型,我们就可以通过静力学分析计算出支座对梁的约束力。
假设梁的长度为 L,集中载荷为 P 作用在距离支座为 a 的位置,支座为固定端。
首先,对整个梁进行受力分析,受到向下的集中载荷 P,支座处有向上的约束力 R 和一个力矩 M。
然后,根据力的平衡条件,在水平方向上没有力的作用,所以合力为零;在垂直方向上,R P = 0,可得 R = P。
再根据对支座处的力矩平衡,M P × a = 0,可得 M = P × a 。

静力学平衡状态下物体受力的分析与计算在静力学中,平衡是指一个物体处于静止状态或者匀速直线运动状态下,其受力合力为零的状态。
而静力学平衡状态下,物体的受力情况可以通过受力分析和计算来确定。
本文将就静力学平衡状态下物体受力的分析与计算进行探讨。
一、问题引入在物体处于静力学平衡状态下时,其受力情况可以通过作用在物体上的外力以及物体本身的重力来描述。
为了方便分析与计算,我们通常将外力分为水平方向的力和垂直方向的力。
二、受力分析在进行受力分析时,我们首先需要明确物体所受到的所有外力和重力的大小、方向以及作用点位置。
接下来,我们可以将这些受力以矢量的形式表示出来,并进行合力分解。
1. 合力分解对于物体所受到的多个力,我们可以将其分解为水平力和垂直力。
通过合力分解,我们可以得到水平方向上的合力以及垂直方向上的合力。
2. 力的平衡条件在静力学平衡状态下,物体所受的水平力和垂直力的合力都必须为零。
即所有水平方向上的力合力为零,所有垂直方向上的力合力为零。
根据这个原理,我们可以得到静力学平衡的两个基本条件:(1)∑F_horizo ntal = 0:物体受到的所有水平方向的力合力为零。
(2)∑F_vertical = 0:物体受到的所有垂直方向的力合力为零。
三、受力计算一旦我们完成了受力分析,我们就可以进行受力计算,并求解静力学平衡状态下物体所受到的各个力的大小。
1. 力的计算对于物体所受到的各个力,我们可以通过力的计算公式或者力的分解来求解其大小。
2. 力的方向在求解力的大小之后,我们还需要确定力的方向。
根据受力分析的结果,我们可以发现物体所受到的力的方向往往与物体所受到的支撑或者施力对象有关。
3. 力的作用点除了力的大小和方向外,力的作用点也是非常重要的。
力的作用点决定了力矩的大小,是静力学计算的关键。
四、力矩的计算对于物体所受到的力,除了进行合力分解和力的计算外,我们还可以通过力矩的计算来获得更多的受力信息。

静力学力的平衡与受力分析在物理学中,力是物体之间相互作用的结果,是描述物体受到的外界作用的量。
静力学力的平衡与受力分析是力学中的重要概念和方法。
本文将通过对静力学平衡和受力分析的讨论,阐述力的平衡条件以及如何进行受力分析。
静力学平衡的概念使我们能够了解物体在静止状态下所受的力的关系。
在一个封闭的系统中,如果物体保持静止,则该物体的受力和力的矩之和为零。
这可以用以下公式表示:ΣF = 0其中,ΣF表示所有作用在物体上的力的矢量和。
这个方程称为力的平衡条件,它是静力学平衡的基础。
平衡条件的主要应用在于解决各种物体和结构的受力问题。
通过对平衡条件的分析,我们可以确定物体上受力的大小、方向和作用点的位置。
在进行受力分析时,我们首先需要明确物体所处的受力系统。
受力系统包括物体所受的所有外力和内力。
外力是由外界环境对物体施加的力,如重力、摩擦力等。
内力是物体内部不同部分之间相互作用的力,如张力、弹力等。
确定了受力系统后,我们可以使用受力分析方法来计算物体所受力的大小和方向。
下面介绍几种常见的受力分析方法:1. 自由体图法:将物体从整体中分离出来形成自由体,只考虑物体受到的力,不考虑周围物体的作用。
通过绘制自由体图,我们可以清楚地看到物体所受的各个力的大小和方向,从而计算出受力平衡的条件。
2. 悬挂点法:对于悬挂在一定点上的物体,我们可以通过设定悬挂点作为坐标原点,建立力的平衡方程来求解物体所受的力。
通过受力分析,我们可以确定物体所受力的大小、方向和作用点的位置。
3. 斜面分解法:对于放置在斜面上的物体,我们可以将受力分解为平行和垂直于斜面的分力,通过受力分析得到物体所受力的大小和方向。
受力分析在工程学和物理学中有着广泛的应用。
它可以帮助我们解决各种实际问题,如桥梁的结构稳定性分析、机械装置的设计优化等。
除了上述介绍的受力分析方法,还有其他一些分析方法,如向量分解法、平衡方程法等。
不同的问题需要选择合适的受力分析方法,以便得到准确的结果。

第一章静力学【竞赛知识要点】重心共点力作用下物体的平衡物体平衡的种类力矩刚体的平衡流体静力学(静止流体中的压强)【内容讲解】一.物体的重心1.常见物体的重心:质量均匀分布的三角板的重心在其三条中线的交点;质量均匀分布的半径R的半球体的重心在其对称轴上距球心3R/8处;质量均匀分布的高为h的圆锥体的重心在其对称轴上距顶点为3h/4处。
2.重心:在xyz 三维坐标系中,将质量为m的物体划分为质点m1、m2、m3……m n.设重心坐标为(x0,y0,z0),各质点坐标为(x1,y1,z1),(x2,y2,z2)……(x n,y n,z n).那么:mx0=∑m i x i my0=∑m i y i mz0=∑m i z i【例题】1、(1)有一质量均匀分布、厚度均匀的直角三角板ABC,∠A=30°∠B=90°,该三角板水平放置,被A、B、C三点下方的三个支点支撑着,三角板静止时,A、B、C三点受的支持力各是N A、N B、N C,则三力的大小关系是.(2)半径为R的均匀球体,球心为O点,今在此球内挖去一半径为0.5R的小球,且小球恰与大球面内切,则挖去小球后的剩余部分的重心距O点距离为.2、如图所示,质量分布均匀、厚度均匀的梯形板ABCD,CD=2AB,求该梯形的重心位置。
3、在质量分布均匀、厚度均匀的等腰直角三角形ABC(角C为直角)上,切去一等腰三角形APB,如图所示。
如果剩余部分的重心恰在P点,试证明:△APB的腰长与底边长的比为5:4.4、(1)质量分别为m,2m,3m……nm的一系列小球(可视为质点),用长均为L的细绳相连,并用长也是L的细绳悬于天花板上,如图所示。
求总重心的位置5、如图所示,质量均匀分布的三根细杆围成三角形ABC,试用作图法作出其重心的位置。
6、如图所示,半径为R圆心角为θ的一段质量均匀分布的圆弧,求其重心位置。
7、论证质量均匀分布的三角形板的重心在三条中线的交点上8、求半径为R的厚薄均匀的半圆形薄板的重心9、均匀半球体的重心问题10、均匀圆锥体的重心11、如图所示,有一固定的半径为R 的光滑半球体,将一长度恰好等于R 21、质量为m 的均匀链条搭在球体上,其一端恰在球体的顶点上,并用水平拉力拉住链条使之静止,求拉力的大小。