当前位置：文档之家 › 李雅普诺夫稳定性理论

李雅普诺夫稳定性理论

  • 格式：pptx
  • 大小：1.42 MB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

第5章李雅普诺夫稳定性分析

第5章李雅普诺夫稳定性分析
3
第5章 李雅普诺夫稳定性分析
第五章 李雅普诺夫稳定性分析
5.1 李雅普诺夫意义下的稳定性 5.2 李雅普诺夫第一法(间接法) 5.3 李雅普诺夫第二法(直接法) 5.4 线性定常系统的李雅普诺夫稳定性分析
4
第5章 李雅普诺夫稳定性分析
5.1 李雅普诺夫意义下的稳定性
1．自治系统
没有外输入作用时的系统称为自治系统，可 用如下系统状态方程来描述:
如果时变函数V(x,t)有一个正定函数作为下限， 也就是说，存在一个正定函数W(x) ，使得
V ( x ,t) W ( x), V (0,t) 0, t t0
则称时变函数V(x,t)在域S（域S包含状态空间的 原点）内是正定的。
24
第5章 李雅普诺夫稳定性分析
3. 负定函数：如果-V(x)是正定函数，则标量函数 V(x)为负定函数。
则称平衡状态xe在李雅普诺夫意义下是稳定的。
在上述稳定的定义中，实数δ通常与ε和初始时
刻t0都有关，如果δ只依赖于ε ，而和t0的选取无关，
则称平衡状态是一致稳定的。
9
第5章 李雅普诺夫稳定性分析
5. 渐近稳定性
若系统的平衡状态xe不仅具有李雅普诺夫意 义下的稳定性，且有
lim
t
||
x(t;
x0 ,
(s)
则 m(s) 为矩阵A的最小多项式。
注：换言之，矩阵A的最小多项式就是(sI-A)-1
中所有元素的最小公分母。
17
第5章 李雅普诺夫稳定性分析
例5-1（补充）：判断下述线性定常系统的稳定性
0 0 0
x 0 0
0
x
0 0 1
解：1）系统矩阵A为奇异矩阵，故系统存在无穷

李雅普诺夫稳定性理论

李雅普诺夫稳定性理论

x(t0 , x0 , t0 ) x0 初态

3.平衡状态：
xe f (xe , t) 0 xe 系统的平衡状态 a.线性系统 x Ax x Rn
A非奇异： Axe 0 xe 0
A奇异：
Axe 0 有无穷多个 xe
b.非线性系统
x f (xe ,t) 0 可能有多个 xe

Pij Pji
x x1 x2 xn T
李氏第二法稳定性定理
设 x f (x,t) 1)在 xe 满足 f (0,t) 0
2） xe 0 V (x, t)存在
定理1
若1)
V
(
x,
t
)
正定 xe
2)
V ( x, t )
负定
则 xe渐近稳定
3)若 x V (x)
eg. x1 x1
x2 x1 x2 x23
令 x1 0 x2 0

xe 1

0

0

0 xe3 1
0 xe2 1
5.2李雅普诺夫意义下的稳定
1.李氏意义下的稳定
如果对每个实数 0 都对应存在另一个
实数 ( ,t0 ) 0 满足 x0 xe (,t0)
则平衡状态 xe 是不稳定的
推论1 若 1)V (x,t)正定 2)V(x,t)正半定
3)x 0 V(x,t) 0 则 xe不稳定
推论2 若 1)V (x,t)正定 2)V(x,t)正半定
3)x 0 V(x,t) 0 则 xe 是李雅普
诺夫意义下的稳定
选取李氏函数的方法
1）构造一个二次型函数 V (x,t)

04第四章-李雅普诺夫稳定性理论

04第四章-李雅普诺夫稳定性理论
平衡状态— —又称一致李氏稳定。
几何意义：
当t t0时,系统受扰动,平衡状态受破坏,产生对应初始状态 x0,当t t0后, 运动状态x(t)会发生变化。
若无论多么小球域S( ),总存在一个球域S( ),当
x0 S( )时, x(t)轨线不会超出S( ),则平衡点xe为
Lyapunov意义下稳定。 实际上，工程中的李氏 稳定是临界不稳定
说明：
J P1AP A~J 考察eJt即可看出 e At的有界性
例：
0 0 J1 0 -1
李氏稳定
0 1 J2 0 0
不稳定
0 0 J3 0 0
李氏稳定
0 0 A J1 0 -1
e At
1
0
0
e-t
x(t)
e At x0
1 0
0 e-t
x10
x20
x10
e-t x20
f1
xn
令
x x xe ,
A
f xT
f 2
xe
x1
f2 x2
f2
xn
xe
f
n
fn
fn
x1 x2 xn
则
.
x
x
( xe常数)
判定法：
.
x Ax
(1) A的所有特征值均有负实部,则xe是渐近稳定的, 与R(x)无关. (2) A的特征值至少有一个有正实部,则xe是不稳定的, 与R(x)无关. (3) A的特征值至少有一个实部为0,则xe的稳定性 与R( x)有关, 不能由A来决定.
P为实对称矩阵 , pij p ji
第二节 李雅普诺夫间接法
李氏间接法利用系统矩阵A的特征值 1, 2,, n 或者说系统极点来判断系统稳定性。

04第四章李雅普诺夫稳定性理论汇总

04第四章李雅普诺夫稳定性理论汇总

04第四章李雅普诺夫稳定性理论汇总李雅普诺夫稳定性理论是数学中一项重要的稳定性理论，对于研究动力系统的稳定性具有重要的指导意义。

该理论由俄罗斯数学家李雅普诺夫于19世纪末和20世纪初提出，后经实践证明，被广泛应用于不同领域的研究中。

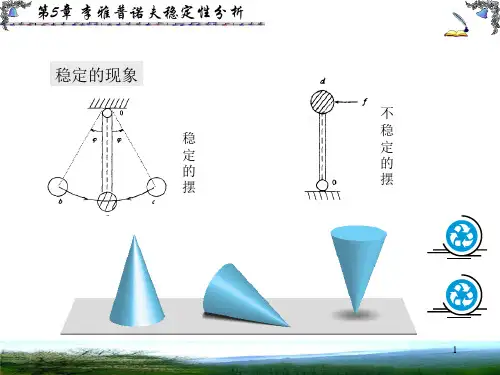
李雅普诺夫稳定性理论的核心思想是通过构造李雅普诺夫函数来分析系统的稳定性。

李雅普诺夫函数是一个满足一定条件的实数函数，它能够度量系统中各个状态的变化情况，并通过数学分析得出系统状态的稳定性。

在李雅普诺夫稳定性理论中，一般使用正定函数来构造李雅普诺夫函数。

对于一个动力系统，假设其状态空间为n维实数向量，系统的演化过程可以表示为一个关于状态变量的微分方程。

为了判断系统在其中一状态的稳定性，需要构造一个函数V(x)，其中x表示状态变量。

如果函数V(x)满足以下两个条件：1.V(x)是正定函数，即对于所有的x，都有V(x)>0，且只有在x=0时，V(x)=0成立。

2.对于系统中任意两个状态x1和x2，如果V(x2)>V(x1)，则在系统演化的过程中，x2的状态比x1更不稳定。

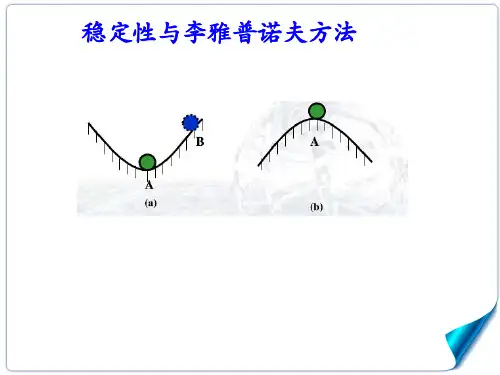
那么，可以推导出系统在状态x=0附近的稳定性。

如果对于所有的状态x，有V(x)>V(x=0)，那么系统就是在x=0处的稳定点。

如果只有在x=0附近，存在一个圆盘区域，使得对于所有的状态x，有V(x)>V(x=0)，那么系统就是局部稳定的。

通过构造李雅普诺夫函数，可以得出系统的稳定性信息。

对于局部稳定性，可以通过计算雅普诺夫函数的导数来得到更详细的信息。

如果导数小于零，则系统是渐进稳定的；如果导数等于零，则系统是边界稳定的；如果导数大于零，则系统是不稳定的。

李雅普诺夫稳定性理论不仅适用于连续系统，也适用于离散系统。

对于离散系统，李雅普诺夫函数的构造和分析方式与连续系统类似，只是微分方程变为差分方程。

总结起来，李雅普诺夫稳定性理论是一种基于构造李雅普诺夫函数来分析系统稳定性的方法。

通过构造正定函数，可以得出系统的稳定性信息，并通过李雅普诺夫函数的导数来得到更详细的稳定性判断。

李雅普诺夫稳定性

李雅普诺夫稳定性

x bx5
这时线性化方法不能用来判断它的稳定性。
李雅普诺夫理论基础
例：证明下面单摆的平衡状态 ( , 0) 是不稳定的。
MR2 b MgR sin 0
式中 R 为单摆长度，M 为单摆质量， b 为铰链的摩擦系数，
g 是重力常数。(系统的平衡点是什么？)
在 的邻域内
sin sin cos ( ) h.o.t. ( ) h.o.t. 设 ~ ，那么系统在平衡点附近的线性化结果是
以速度 1 指数收敛于 x 0 。
例2：系统 x x2 , x(0) 1它的解为 x 1/(1 t)，是个慢于任 何指数函数 et ( 0) 的函数。
3、局部与全部稳定性
定义：如果渐近（或指数）稳定对于任何初始状态都能 保持，那么就说平衡点是大范围渐近（或指数）稳定的， 也称为全局渐近（或指数）稳定的。
李雅普诺夫理论基础
§2.2 线性化和局部稳定性
李雅普诺夫线性化方法与非线性系统的局部稳定性有关。
Lyapunou线性化方法说明：在实际中使用线性控制方法基
本上是合理的。
对于自治非线性系统 x f (x) ，如果 f (x) 是连续可微的,那
么系统的动态特性可以写成( f (0) 0 )：
x
f x
李雅普诺夫理论基础
第二章 Lyapunov理论基础
稳定性是控制系统关心的首要问题。
稳定性的定性描述：如果一个系统在靠近其期望工作点的某 处开始运动，且该系统以后将永远保持在此点附近运动， 那么就把该系统描述为稳定的。
例如：单摆，飞行器 李雅普诺夫的著作《动态稳定性的一般问题》，并于1892
年首次发表。 1. 线性化方法：从非线性系统的线性逼近的稳定性质得出非

李雅普诺夫关于稳定性的定义

李雅普诺夫关于稳定性的定义

✓
线性定常系统的有界输入有
界输出(BIBO)稳定性
未研究系统的内部状态变化的稳定性，也不能推广 到时变
系统和非线性系统等复杂系统。
➢ 再则，对于非线性系统或时变系统，虽然通过一些 系统转化方法，上述稳定判据尚能在某些特定系统和范 围内应用，但是难以适用于一般系统。
现代控制系统的结构比较复杂，大都存在非线性或时变因 素，即使是系统结构本身，往往也需要根据性能指标的要 求而加以改变，才能适应新的情况，保证系统的正常或最 佳运行状态。
Lyapunov的博士论文被译成法文并于1907年发表，1949年 普林斯顿大学出版社重印了法文版。1992年在Lyapunov的 博士论文发表100周年之际，International Journal of Control （国际控制杂志）以专辑形式发表了Lyapunov论文的英译 版，以纪念他在控制理论领域所作的卓越贡献。
➢ 该方法不仅可用于线性系 统而且可用于非线性时变 系统的分析与设计，已成 为当今控制理论课程的主 要内容之一。
➢ 百余年来Lyapunov理论 得到极大发展, 在数学、 力学、自动控制、机械工 程等领域得到广泛应用。
A.M. Lyapunov是一位天才的数学家。曾从师于大数学家 P.L. Chebyshev（切比雪夫），和A.A. Markov（马尔可夫 ）是同校同学（李比马低两级），并同他们始终保持着良好 的关系。他们共同在概率论方面做出了杰出的贡献。在概率 论中可以看到关于矩的马尔可夫不等式、切比雪夫不等式和 李亚普诺夫不等式等。Lyapunov还在相当一般的条件下证 明了中心极限定理。
✓
经典控制理论讨论的有界输入
有界输出（BIBO）稳定即为外部稳定性 。
Outer stability

李雅普诺夫稳定性的定义

李雅普诺夫稳定性的定义

x(0) x(0)
x1
? 定义 (李雅普诺夫稳定性) 若状态方程
x2
x'=f(x,t) 所描述的系统,
? 对于任意的?>0和任意初始时刻t0,
??
x(0) x(0)
x1
? 都对应存在一个实数?(?,t0)>0,
? 使得对于任意位于平衡态xe的球域 S(xe,?)的初始状态x0,
? 当从此初始状态x0出发的状态方程的解x都位于球域 S(xe,?)内,
? 它是一种具有普遍性的稳定性理论, 不仅适用于线性 定常系统,而且也适用于非线性系统、时变系统、分 布参数系统。
? 本节先讨论李雅普诺夫稳定性理论的基础--李雅普 诺夫稳定性定义。
平衡态
? 设我们所研究的系统的状态方程为 x'=f(x,t)
其中x为n维状态变量; f(x,t)为n维的关于状态变量向量x和时间t的非线性向量函数。 ? 对该非线性系统,其平衡态的定义如下。
? 则系统在初始时刻t0的平衡态xe 为在李雅普诺夫意义下稳定的。
x2
??
x(0) x(0)
x1
? 以二维状态空间为例,上述定义的几何解释和状态轨线变 化如图所示。
? 对于李雅普诺夫稳定性，还有如下说明：
? 李雅普诺夫稳定性针对平衡状态而言，反映的是平衡状 态邻域的局部稳定性，即小范围稳定性。
? 系统做等幅振荡时，在平面上描出一条封闭曲线，只要 不超过S(xe,?)，就是李雅普诺夫稳定的，而经典控制理 论则认为不稳定。
? 因此,不失一般性,为了便于分析,我们常把平衡态取为状 态空间的原点。
? 值得指出的是，由于非线性系统的李雅普诺夫稳定性具有局 部性特点,因此在讨论稳定性时,通常还要确定平衡态的稳定邻 域(区域)。

李雅普诺夫Lyapunov稳定性理论李雅普诺夫

李雅普诺夫Lyapunov稳定性理论李雅普诺夫

现代控制理论的稳定性判据
李雅普诺夫（Lyapunov）稳定性理论
李雅普诺夫（Lyapunov）稳定性理论
李雅普诺夫，俄国数学力学专家， 俄罗斯科学院院士，意大利林琴 科学院 以及法国巴黎科学院的外籍院士。 1892年在他的博士论文《运动稳定性的一般 问题》（The general problem of the stability motion） 中系统地研究了由微分方程描述的一般运动系统的稳定性 问题，建立了著名的Lyapunov方法，为现代控制和非线性 控制奠定了基础。 Lyapunov稳定性理论对于控制理论学科的发展产生了深刻 的影响，已成为现代控制理论的一个非常重要的组成部分。
时，从任意初态出发的解始终位于以 x e 为球心，半径为 的闭 球域S ( ) 内，即
x(t; x0 , t0 ) xe , t t0
则称系统的平衡状态 x 在李雅普诺夫意义下稳定。
e
当系统做不衰减的震荡运动
时，将描绘出一条封闭曲线 ，只要不超出 S ( ) ，则认为是 稳定的。
初始状态有界，随时间
推移，状态向量距平衡 点的距离可以维持在一 个确定的数值内，而到 达不了平衡状态。
x2
S ( )
xe
S ( )
x1
任给一个球域S ( ) ，若存在一个球域S ( ) ，使得从 S ( )出发的 轨迹不离开S ( )，则称系统的平衡状态是李雅普诺夫意义下稳定 的。 若 与初始时刻 t 0无关，则 称系统的平衡状态x e是一致
x2
S ( )
xe
S ( )
x1
近，直至到达平衡状态后
停止运动。
3、大范围渐近稳定 当初始条件扩展到整个状态空间，且平衡状态均具 有渐近稳定性时，称此平衡状态是大范围渐近稳定的。 几何意义：

第四章李雅普诺夫稳定性理论

第四章李雅普诺夫稳定性理论

对概念的几点说明：
(5)线性系统渐近稳定等价于大范围渐近稳定。对非线 性系统,一般只考虑吸引区为有限定范围的渐近稳定。
第二节 李雅普诺夫间接法
思想：李氏间接法利用系统矩阵A的特征值 或者说系统极点来判断系统稳定性。
一、线性定常系统的稳定性
线性定常系统的稳定性判别定理：
(1)李氏稳定 A的约当标准形J中，实部为0的特征 值所对应的约当块的维数是一维的，其余特征值均 有负实部。 (2)渐近稳定 A的特征值均具有负实部。
，其中P为实对
称方阵，它的元素可以是定常的，可以是时变的，但
V(x)并不一定都是简单的二次型。
(4) V(x)函数只表示系统在平衡状态附近某邻域内局部运动的 稳定情况，但丝毫不能提供邻域外运动的任何信息。
(5) 由于V(x)构造需要技巧，因此Lyapunov第二法主要用 于那些使用别的方法无效或难以判断其稳定性的问题，如 高阶非线性系统或时变系统。
A奇异：
b. 非线性系统 例：
令
2. 孤立的平衡状态：在某一平衡状态的充分小的 邻域内不存在别的平衡状态。
说明： (1) 系统不一定都存在平衡点； (2) 但系统也可能有多个平衡点； (3) 平衡点多数在状态空间的原点，可通过适当
的坐标变换移到原点（针对孤立平衡点）； (4) 稳定性问题都是相对于某个状态而言的，对
(3)不稳定 A的特征值中至少有一个有正实部。
说明：
(1)劳斯判据依然适用。 (2)状态稳定(内部的稳定)与BIBO稳定(输出稳定性)。
解释： 例1：
李氏稳定 不稳定 李氏稳定
李氏稳定 不稳定
例2：
求A的特征值： 得A特征值：
不稳定
二、非线性系统的稳定性 非线性系统的稳定性一般是局部的。用间接法判

第五章 李雅普诺夫稳定性理论

第五章 李雅普诺夫稳定性理论

非线性系统的稳定性是相对系统的平衡态而言的， 非线性系统的稳定性是相对系统的平衡态而言的，很难 笼统地讨论非线性系统在整个状态空间的稳定性。 笼统地讨论非线性系统在整个状态空间的稳定性。 对于非线性系统， 对于非线性系统，其不同的平衡态有着不同的稳定 故只能分别讨论各平衡态附近的稳定性。 性，故只能分别讨论各平衡态附近的稳定性。 对于稳定的线性系统，由于只存在唯一的孤立平衡 对于稳定的线性系统， 态，所以只有对线性系统才能笼统提系统的稳定性 问题。 问题。 李雅普诺夫稳定性理论讨论的是动态系统各平衡态 附近的局部稳定性问题。 附近的局部稳定性问题。 它是一种具有普遍性的稳定性理论， 它是一种具有普遍性的稳定性理论，不仅适用于线 性定常系统，而且也适用于非线性系统、时变系统、 性定常系统，而且也适用于非线性系统、时变系统、 分布参数系统。 分布参数系统。
5.1 动态系统的外部稳定性
控制系统的外部稳定性，常称为有界输入有界输出稳定性。 控制系统的外部稳定性，常称为有界输入有界输出稳定性。 在讨论系统的外部稳定性时，一般只适用于线性动态系统， 在讨论系统的外部稳定性时，一般只适用于线性动态系统， 而且必须假定系统的初始条件为零。 而且必须假定系统的初始条件为零。 外部稳定性的定义是，初始条件为零的线性系统， 外部稳定性的定义是，初始条件为零的线性系统，在任何一 个有界的输入作用下，若系统所产生的输出也是有界的， 个有界的输入作用下，若系统所产生的输出也是有界的，就 称该动态系统是外部稳定的，又称为BIBO稳定。 稳定。 称该动态系统是外部稳定的，又称为 稳定 对于单输入单输出线性定常系统而言， 对于单输入单输出线性定常系统而言，在经典控制理论中定 义的传递函数正是表征了系统在零初始条件下， 义的传递函数正是表征了系统在零初始条件下，输出量与输 入量两者间的关系。因此，对线性定常系统， 入量两者间的关系。因此，对线性定常系统，具有外部稳定 性的充要条件等价于其传递函数的所有极点都位于s平面的 性的充要条件等价于其传递函数的所有极点都位于 平面的 左半边。 左半边。

稳定性与李雅普诺夫

稳定性与李雅普诺夫
1）V(x) ＞ 0，则称V(x)为正定。例如V(x)=x12 +x22； 2）V(x) ≥ 0，则称V(x)为半正定（或非负定）。例如
V(x)=(x1 +x2)2； 3）V(x) ＜ 0，则称V(x)为负定。例如V(x)=－(x12 +2x22)； 4）V(x) ≤ 0，则称V(x)为半负定（或非正定）。例如
p
Δ1
p11 ， Δ2
11
p
21
p
12
p
，…
， Δn P
22
矩阵 P（或 V(x)）定号性的充要条件是：
1）若 Δi 0, i (1,2,, n) ，则 P（或 V(x)）为正定；
2）若
Δi
0, 0,
i为偶数 i为奇数
，则
P（或
V(x)）为负定；
3）若
Δi
0, 0,
i i
(1,2,, n
需要根据舍弃旳髙 阶项再分析 采用李雅普诺夫第 二法
举例：用李雅普诺夫第一法判断下列系统旳稳定性
x1 x1 x1x2
x2
x2
x1x2
第一步：令 x1 0, x2 0
求得系统旳平衡状态 x1e (0,0)T , x1e (1,1)T
第二步：将系统在平衡状态x1e附近线性化
f1 f1
（1）V(x)是满足稳定性判据条件的一个正定的标量函数，且 对于 x 应具有连续的一阶偏导数； （2）对于一个给定系统，如果 V(x)可以找到，那么通常是非 唯一的，这并不影响结论的一致性。 （3）V(x)的最简单形式是二次型函数 V(x) = xTP x，其中 P 为 实对称方阵，它的元素可以是定常的或时变的。但 V(x)并不一 定都是简单的二次型。 （4）如果 V(x)为二次型，且可表示为：

自动控制理论 第10章 李雅普诺夫稳定性分析

自动控制理论 第10章 李雅普诺夫稳定性分析

２）如果ｘｅ＝０为系统的平衡状态，则李氏函数应满足Ｖ（ｘｅ）＝ Ｖ（０）＝０。但当ｘ（ｔ）≠ ０
时， 不管其分量大于零或小于零，均能使Ｖ（ｘ）＞０。
基于上述的性质，人们常以状态矢量ｘ的二次型函数Ｖ（ｘ）作为李氏函数
的候选函数，即
式中，ｘ为实变数矢量。只要矩阵Ｐ是正定的，则上式所示的Ｖ（ｘ）就符 合对李氏函数性质的要求。
对于连续定常系统，李雅普诺夫第二方法是根据Ｖ（ｘ）和
的性
质去判别它的稳定性。因此需要研究以下两个问题：
１）具备什么条件的函数才是李雅普诺夫函数，简称李氏函数。
２）怎样利用李氏函数去判别系统平衡状态的稳定性？
由对图10-2所示系统的讨论，可知李氏函数必须要同时具有如下两个性质：
１）李氏函数是自变量为系统的状态矢量ｘ（ｔ）的标量函数。
态是不稳定的。
2021/6/18
第十章 李雅普诺夫稳定性分析
6
为了能更直观地理解上述平衡状态稳定性的概念，
下图在二维状态平面上分别画出了系统平衡状态的稳 定、渐近稳定和不稳定３种情况。
2021/6/18
第十章 李雅普诺夫稳定性分析
7
自动控制理论
第二节 李雅普诺夫第二方法
正定函数
2021/6/18
11
自动控制理论
由上式可见，除了ｘｅ＝０外，系统的能量Ｖ（ｘ）在运动过程中由于 受到了阻尼器的阻尼作用而不断地减小，最后使Ｖ（ｘ）＝０。这个例子很 容易把能量函数Ｖ（ｘ）与实际系统联系起来。然而，对一般的系统而言， 至今还没有一个普遍适用“能量函数” 的表达式。对此，李雅普诺夫提出了 一个虚拟的能量函数，人们称它为李雅普诺夫函数，用Ｖ（ｘ）表示。
则称系统的平衡状态ｘｅ是渐近稳定的。

《现代控制理论》李雅普诺夫稳定性分析

《现代控制理论》李雅普诺夫稳定性分析
向量和矩阵的范数
1、向量空间上的欧几里德范数（即向量长度）
其欧几里德范数定义为：
一般
一、向量和矩阵的范数
预备知识
矩阵范数
矩阵 的范数定义为：
【例】
Hale Waihona Puke ， 则即:矩阵每个元素平方和开根号
预备知识
2、矩阵范数
1．二次型函数：由n个变量
组成的二次齐次多项式，称（n元）二次型函数
2．二次型函数的矩阵表示
则系统在原点处的平衡状态是不稳定的。
为唯一的平衡状态。
定理4：设系统状态方程为
李雅普诺夫主要的稳定性定理
例题
[例] 设系统状态方程为
试确定系统的稳定性。
解 xe=0
,
是该系统惟一的平衡状态。
由于当
时
,所以系统在原点处的平衡状态是
大范围渐近稳定的。
选取
李雅普诺夫主要的稳定性定理
例题
[例] 已知定常系统状态方程为
定义：若所有有界输入引起的零状态响应输出有界，则称系统为有界输入输出稳定。
李雅普诺夫第一方法—间接法
定理3：连续定常系统 传递函数为： 系统 BIBO 稳定的充要条件为：传递函数的所有极点均位于S左半平面。
【例】试分析系统渐近稳定和BIBO稳定。
李雅普诺夫主要的稳定性定理
讨论续
这是一个矛盾的结果,表明
也不是系统的
受扰运动解。综合以上分析可知,
当
时,显然有
根据定理9-12可判定系统的原点平衡状态是大范围渐近稳定的。
李雅普诺夫主要的稳定性定理
线性系统稳定性分析
一.线性定常系统李雅普诺夫稳定性分析
线性定常连续系统
系统状态方程为

李雅普诺夫稳定性理论

李雅普诺夫稳定性理论

❖推论. 1：当 V(x,t) 正定，V( x, t ) 半正定， 且 V[x(t; x0,t),t]在非零状态不恒为零时,则
原点不稳定。
.
❖推论2：V(x,t) 正定，V ( x , t ) 半正定，若
x0 ，V(x,t) 0 ，则原点是李雅普
诺夫意义下稳定(同定理3)。
几点说明：
1) V(x,t)选取不唯一，. 但没有通用办法，V(x,t)
其中是任选的微量，则称系统的平衡状态xe是 渐近稳定的。
定义三 对所有的状态(状态空间的所有点)，如 果由这些状态出发的轨迹都具有渐近稳定性，则 称平衡状态xe为大范围渐近稳定。
定义四 :如果从球域 S( )出发的轨迹，无论球
域选得多么小，只要其中有一条轨迹脱离球域， 则称平衡状态xe为不稳定。
❖线性系统：如果它是渐近稳定的，必是有大 范围渐近稳定性(线性系统稳定性与初始条件的 大小无关)。
例
xx21 kxx21 k 0
V (x ,t)x 1 2 k2 2x(k 0 )
V ( x , t ) 2 x 1 x 1 2 k 2 x 2 x 2 k 1 x 2 x 2 k 1 x 2 x 0
故系统是李雅普诺夫意义下的稳定
定理四 设系统的状态方程为 xf(x,t) f(0 ,t)0 (tt0) 如果存在一个标量函数V(x，t)，V(x，t)对向量x中 各分量具有连续的一阶偏导数，且满足条件：
矩阵P(或V(x))定号性的充要条件是:
(1) 若Δi >0 (i=1,2,…n),则P为正定;
(2) 若
0 i0
ii为 为奇 偶数 数 ，则 P为负定
(3) 若
0 i 0
i1,2,,n1 in
，P 则 为半正定

李雅普诺夫稳定性分析

李雅普诺夫稳定性分析
第四章
李雅普诺夫稳定性分析
李雅普诺夫稳定性理论
李雅普诺夫理论在建立一系列关于稳定性概念的基础上，提出了判断 系统稳定性的两种方法： 间接法：利用线性系统微分方程的解来判断系统稳定性，又称之为李 雅普诺夫第一法； 直接法：首先利用经验和技巧来构造李雅普诺夫函数，进而利用李雅 普诺夫函数来判断系统稳定性，又称为李雅普诺夫第二法。
这表明， 当且仅当‖eAt‖≤ k ＜∞ 时，对任给的一个实数ε > 0，都对应存在和初始时 刻无关的一个实数 δ(ε)= ε /k，使得由满足不等式 ||x0 — xe|| ≤ δ(ε) (4-391) 的任一初态x0出发的受扰运动都满足不等式 xt; x0 ,0 xe e At x0 xe k , t 0 (4 392)
2)
证明 1) 设 xe 为线性定常系统(4-388+)的平衡状态，则由性质 e 0 和 Axe 0 x 可知，对于所有 t≥0 均有（可通过等式两边求微分证明下式）
xe e At xe (4 389) (4 390)
于是，考虑到 x(t; x0, 0) = eAtx0，有
x(t; x0 ,0) xe e At ( x0 xe ), t 0
2 李雅普诺夫意义下的稳定性
设系统初始状态位于以平衡状态xe为球心、δ为半径的闭球域S(δ)内，即 ||x0 - xe|| ≤ δ， t =t0 (4-385) 若能使系统方程的解x(t；x0，t0)在t→∞的过程中，都位于以xe为球心、任意规 定的半径为ε的闭球域S(ε)内，即 ||x(t；x0，t0)-xe|| ≤ ε，t≥t0 (4-386) 则称系统的平衡状态xe在李雅普诺夫意义下是稳定的。式中||· ||为欧几里德范 数，其几何意义是空间距离的尺度。 例如： ||x0 - xe||表示状态空间中， x0 点至 xe 点之间距离的尺度，数学表达式 为： ||x0 - xe|| = [(x10 – x1e)2+ (x20 – x2e)2+… +(xn0 – xne)2]1/2 (4-385)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
非线性系统的分类： 非本质非线性 能够用小偏差线性化方法进行线性化处理的非线性。 本质非线性 用小偏差线性化方法不能解决的非线性。
1.1 非线性系统相关基本概念
非线性系统的稳定性 （1）非线性系统的稳定性，则除了与系统的结构、参数 有关外，很重要的一点是与系统起始偏离的大小密切相连。
（2）不能笼统地泛指某个非线性系统稳定与否，而必须 明确是在什么条件、什么范围下的稳定性。
平衡态为孤 立的平衡态。
1.2 李雅普诺夫稳定性及判别方法
4) 对于线性定常系统 x f [x,t，] 当A为x 非奇异矩阵时，
的解Axe 是0 系统唯xe一存0在的平衡状态，当A为非奇异时，则
会有无穷多个。xe
5) 由于任意一个已知的平衡状态,都可以通过坐标变换将其变
换到坐标原点 xe 处0。所以今后将只讨论系统在坐标原点处的
第一讲 李雅普诺夫稳定性理论
目录
非线性系统相关基本概念 李雅普诺夫关于稳定性的定义
及李雅普诺夫第一，第二方法 拉塞尔不变集理论 Barbalat引理 类李雅普诺夫引理 稳定性分析方法概述 一致最终有界
1.1 非线性系统相关基本概念
非线性系统的定义： 含有非线性元件的系统，称之为非线性系统。
与稳定性相关的几个定义 x xe ：状态向量x与平衡状态 xe 的距离。
点集s()：以xe为中心，为半径的超球体。 若xs() ： 则 x xe ，其中 x xe 为欧几里德范数。 当很小时，则称s()为xe的邻域。 如系统的解 x (t; x0 ,t0 ) 位于球域s()内，则：
(t; x0 , t0 ) xe , t t0 表明系统由初态x0或短暂扰动所引起的自由响应是有界的。
稳定性就可以了。 6) 稳定性问题都是相对于某个平衡状态而言的。(这一点从线 性定常系统中的描述中可以得到理解) 7) 如果一个系统有多个平衡点。由于每个平衡点处系统的稳 定性可能是不同的。对有多个平衡点的系统来说，要讨论该 系统的稳定性必须逐个对各平衡点的稳定性都要逐个讨论。
1.2 李雅普诺夫稳定性及判别方法
1.1 非线性系统相关基本概念
回环（间隙）特性
x1表示输入 x2表示输出
b 表示间隙。
1.1 非线性系统相关基本概念 回环（间隙）特性的影响
降低了定位精度，增大了系统的静差。 使系统动态响应的振荡加剧，稳定性变坏。
1.1 非线性系统相关基本概念 继电器特性
(a)理想继电特性 (b)死区继电特性 (c)一般的继电特性
t的函数；一般f 为时变的非线性函数，如果不含t，则为定常
的非线性函数.。
设(1-1)在给定初始条件 (t0 x0 ) 下,有唯一解：
x (t, x0,t0 )
(1-2)
式(1-2)描述了系统(1-1)在n维状态空间中从初始条件 (t0 x0出) 发
的一条状态运动的轨迹，简称为系统的运动和状态轨线。
减小了系统的开环增益，提高了系统的平稳 性，减弱动态响应的振荡倾向。
1.1 非线性系统相关基本概念
饱和特性
x1 ，a等效增益为常值， 即线性段斜率；
而 x1 ，a输出饱和，等
效增益随输入信号的加 大逐渐减小。
1.1 非线性系统相关基本概念
饱和特性的影响 饱和特性使系统开环增益下降， 对动态响应的平稳 性有利。 如果饱和点过低，则在提高系统平稳性的同时，将 使系统的快速性和稳态跟踪精度有所下降。 带饱和的控制系统，一般在大起始偏离下总是具有 收敛的性质，系统最终可能稳定，最坏的情况就是 自振，而不会造成愈偏愈大的不稳定状态。
1.2 李雅普诺夫稳定性及判别方法
李雅普诺夫根据系统自由响应是否有界把系统的稳定性定义为 四种情况：李雅普诺夫意义下的稳定、渐近稳定、大范围渐近 稳定、不稳定。
几 种 典 型 的 非 线 性 特 性
1.1 非线性系统相关基本概念
不灵敏区（死区）特性
x1表示输入 x2表示输出
△ 表示不灵敏区， 也常称死区。
1.1 非线性系统相关基本概念
不灵敏区（死区）特性的影响
当系统前向通道中串有死区特性的元件时， 最主要的影响是增大了系统的稳态误差，降 低了定位精度。
解析 方法
SISO的代数 分析方法
1892年俄国数 学家李雅普诺夫
Routh判据 Houwitz判据
第一 方法
第二 方法
根据SISO闭环特 征方程的系数判
定系统的稳定性
根据状态方程A阵 判定系统的稳定性
1.2 李雅普诺夫稳定性及判别方法
关于李雅普诺夫稳定性的基本概念
系统的结构
系统的参数
线性系统的稳定性 系统的结构和参数 初始条件 外界信号的类型和大小
1.1 非线性系统相关基本概念
非线性系统的运动形式 （1）非线性系统在小偏离时单调变化，大偏离时 很可能就出现振荡。 （2）非线性系统的动态响应不服从叠加原理。
1.1 非线性系统相关基本概念
非线性系统的自振 非线性系统的自振却在一定范围内能够长期存在，性系统相关基本概念
1.2 李雅普诺夫稳定性及判别方法
系统的平衡状态：若系统(1-1)存在状态矢量 xe ，对所有t，
使得：
f (xe , t) 0
(1-3)
成立，则称 xe 为系统的平衡状态。
说明:
1）对于任一个系统,不一定都存在平衡状态.
2) 如果一个系统存在平衡状态,其平衡状态也不一定是唯一的.
3) 当平衡态的任意小邻域内存在系统的别的平衡态时，称此
1.1 非线性系统相关基本概念
继电器特性的影响
理想继电控制系统最终多半处于自振工作状态。 可利用继电控制实现快速跟踪。 带死区的继电特性，将会增加系统的定位误差，对
其他动态性能的影响，类似于死区、饱和非线性特 性的综合效果。
1.2 李雅普诺夫稳定性及判别方法
线性系统稳定性分析的理论框架 稳定性分析
非线性系统的稳定性
李雅普诺夫第二方法是一种普遍适用于线性系统、非线性 系统及时变系统稳定性的分析的方法。李雅普诺夫给出了 对任何系统都普遍适用的稳定性的一般定义。
1.2 李雅普诺夫稳定性及判别方法
系统状态的运动及平衡状态
状态轨迹：设所研究系统的齐次状态方程为
x f [x,t]
(1-1)
式中：x—n维状态矢量；f—与x同维的矢量函数；是 x和i 时间