五年级数学下册(SJ)【知识点总结】第一单元 简易方程
- 格式:doc
- 大小:669.00 KB
- 文档页数:2

苏教版五年级数学下册第一单元简易方程第一节等式与方程等式的性质和解方程一、基础知识1、等式像50+50=100这样用等号连接表示左右两边相等的式子叫做等式。
2、方程(1)概念:像x+50=150、2x=200这样含有未知数的等式是方程。
(2)特征:①是等式②含有未知数3、等式与方程的关系方程一定是等式,等式不一定是方程,等式包括方程,方程是特殊的等式。
4、等式的性质1等式两边同时加上或减去同一个数,所得结果任然是等式,这是等式的性质1。
5、等式的性质2等式两边同时乘或除以同一个不是0的数,所得结果任然是等式,这是等式的性质2。
6、方程的解使方程左右两边相等的未知数的值叫做方程的解。
7、解方程求方程的解的过程叫做解方程。
8、各方程类型的解法(1)a+x=b(2)b-x=a(3)ax=b(a≠0)(4)x÷a=b(a≠0)第二节 各类型方程的解法及习题一、含有加法或减法的方程解形如b a x =±的方程时,运用等式的性质(1),在方程两边同时减去或加上同一个数,使方程的一边只剩下x ,即可求出未知数x 的值。
b a x =±解:a b a a x =±解方程a b x =方程的解1、将方程的书写格式与脱式计算混淆2、利用等式的性质(1)解方程时,等式两边没有同时加或减同一个数二、形如a x b =-的方程的解法例:解方程920=-x 。
解题步骤:第一步 将方程变为b a x =+的形式。
第二步 解方程第三步 检验结果是否正确。
正确解答 920=-x解:x x x +=+-920x +=920209=+x9-209-9=+x11=x检验:右边,,左边右边,左边=====9911-20-20x 所以11=x 是方程的解。
运用代入法解含2个未知数的方程易错点将等式两边交换位置,把形如a x b =-的方程转化为形如b a x =+的方程拓展提升三、解形如)0(≠=a b ax 的方程解形如)0(≠=a b ax 的方程时,根据等式的性质(2),方程两边应同时除以a 。
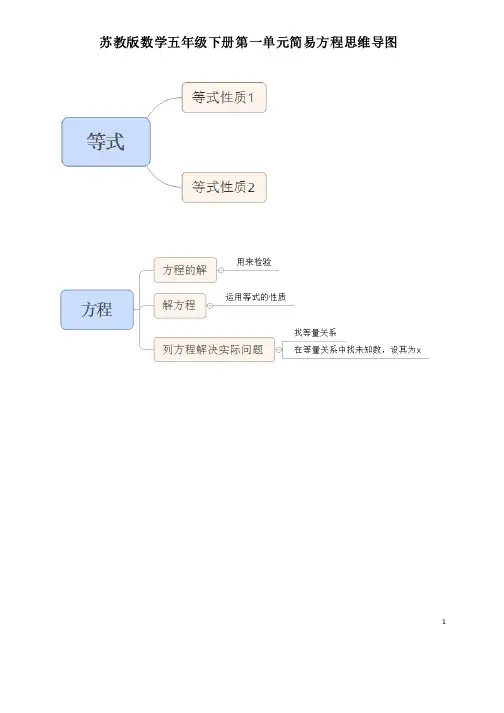
1 苏教版数学五年级下册第一单元简易方程思维导图等式和方程的含义等式和方程的含义等式:表示两个数(量)相等关系的式子。
比如3=3,3+4=7,3a+4a=7a ,4x+5=25,x 2=36方程:含有未知数的的等式叫做方程。
比如4x+5=25,x 2=36。
等式和方程之间的关系:等式不一定是方程,方程一定是等式。
练习一、算一算一、算一算5x+7x 8x+3x+12x 9x-5x 32x-19x-8x4(x+1)+3x 3(2x-3)+5(x+1)6x-(2x-3) 40-(30-5x)小结:化简代数式,也叫做合并同类项,同类的合并,不同类的不能合并。
小结:化简代数式,也叫做合并同类项,同类的合并,不同类的不能合并。
二、填空二、填空1.1. 下面的式子中,是等式的在后面(下面的式子中,是等式的在后面( )里画“√”。
)里画“√”。
X+18=36 X+18=36 (( )) x+2 x+2﹥﹥10 10 (( )) 72-x 72-x (( )) x=3 x=3 (( )) 3+4=7 3+4=7 (( )) 2.2. 下面的式子中,是方程的在后面(下面的式子中,是方程的在后面( )里画“√”。
)里画“√”。
X+18=36 X+18=36 (( )) x+2 x+2﹥﹥10 10 (( )) 72-x 72-x (( )) x=3 x=3 (( )) 3+4=7 3+4=7 (( )) 3.3. 在这一些式子①在这一些式子①5.25.25.2++x=9.8x=9.8,②,②,②4.54.54.5--4=0.54=0.5,③,③,③5x 5x 5x<<9.29.2,④,④,④x x ÷1.61.6,⑤,⑤,⑤4.24.24.2÷÷3=1.43=1.4,⑥,⑥,⑥7x 7x 7x÷÷7>1.11.1,,⑦5x=1005x=100,,⑧7+m -n=15中,等式有( )),方程有( ))。

苏教版五下数学第一单元《简易方程》知识点附练习5套第一单元简易方程1、表示相等关系的式子叫做等式。
2、含有未知数的等式是方程。
3、方程一定是等式;等式不一定是方程。
等式>方程4、等式两边同时加上或减去同一个数,所得结果仍然是等式。
这是等式的性质。
5、使方程左右两边相等的未知数的值叫做方程的解。
6、求方程中未知数的过程,叫做解方程。
7、检验格式:60-4x=20解4x=60-204x=40x=10①检验:把x=10代入原方程,左边=60-4×10=20,右边=20,左边=右边,所以x=10是原方程的解.②检验:方程左边=60-4×10=20方程右边所以,x=10是方程的解。
8、解方程时常用的关系式:一个加数=和-另一个加数减数=被减数-差被减数=减数+差一个因数=积÷另一个因数除数=被除数÷商被除数=商×除数9、五个连续的自然数(或连续的奇数,连续的偶数)的和,等于中间的一个数的5倍。
奇数个连续的自然数(或连续的奇数,连续的偶数)的和÷个数=中间数10、4个连续的自然数(或连续的奇数,连续的偶数)的和,等于中间两个数或首尾两个数的和×个数÷2(高斯求和公式)。
11、列方程解应用题的思路:A、审题并弄懂题目的已知条件和所求问题。
B、理清题目的等量关系。
C、设未知数,一般是把所求的数用X表示。
D、根据等量关系列出方程E、解方程F、检验五年级数学(下)解方程练习(1)1.加数+加数=和加数=和-另一个加数例:20+ⅹ=45(ⅹ是一个加数,应用:加数=和-另一个加数方法来解)解:ⅹ=45-20ⅹ=25练习10题:35+ⅹ=10012.5+ⅹ=4547+ⅹ=305 3.5+ⅹ=30.5 60+ⅹ=160.5ⅹ+25=38ⅹ+2.5=3.8ⅹ+3.2=15ⅹ+52=100ⅹ+0.64=64五年级数学(下)解方程练习(2)2、被减数-减数=差被减数=差+减数减数=被减数-差例:ⅹ-51=43(ⅹ是一个被减数,应用:被减数=差+减数方法来解)解:ⅹ=43+51ⅹ=94例:64-ⅹ=20(ⅹ是一个减数,应用:减数=被减数-差方法来解)解:ⅹ=64-20ⅹ=44练习10题:ⅹ-51=68ⅹ-12.5=5ⅹ-14.25=43ⅹ-3.52=2.48ⅹ-12.5=6.894-ⅹ=2042.32-ⅹ=300.64-ⅹ=0.25 100-ⅹ=0.2580-ⅹ=70五年级数学(下)解方程练习(3)3、因数×因数=积因数=积÷另一个因数例:6ⅹ=48(ⅹ是一个因数,应用:因数=积÷另一个因数方法来解)解:ⅹ=48÷6ⅹ=8练习10题:7ⅹ=630.32ⅹ=1600.6ⅹ=4.8625ⅹ=1008ⅹ=720.25ⅹ=400 2.25ⅹ=90025ⅹ=15ⅹ=0.458ⅹ=1000五年级数学(下)解方程练习(4)4、被除数÷除数=商被除数=商×除数除数=被除数÷商例:ⅹ÷9=53(ⅹ是一个被除数,应用:被除数=商×除数方法来解)解:ⅹ=53×9ⅹ=477例:255÷ⅹ=5(ⅹ是一个除数,应用:除数=被除数÷商方法来解)解:ⅹ=255÷5ⅹ=51练习10题:ⅹ÷12=13ⅹ÷0.9=5.3ⅹ÷0.25=2.14ⅹ÷3.2=17ⅹ÷1.2=1.3300 5÷ⅹ=5 2.55÷ⅹ=0.532.8÷ⅹ=0.21000÷ⅹ=83612÷ⅹ=3五年级数学(下)解方程练习(5)5、稍复杂的方程(一)例:2ⅹ-20=4(先把2ⅹ看成一个整体,2ⅹ看成一个被减数,应用:被减数=差+减数方法来解)(最关键是把含有ⅹ的量看成一个整体,还把它看成一个什么数)2ⅹ-20=4解:2ⅹ=4+202ⅹ=24ⅹ=24÷2ⅹ=12练习10题:2ⅹ-51=674ⅹ-3.52=12.4880-10ⅹ=7092-8ⅹ=202×1.02+ⅹ=35.22×7+2ⅹ=3020ⅹ÷8=1254ⅹ÷12=133005÷2ⅹ=5 2.55÷3ⅹ=0.5五年级数学(下)解方程练习(6)6、稍复杂的方程(二)例:(2.8+ⅹ)×2=10.4(先把(2.8+ⅹ)看成一个整体,(2.8+ⅹ)看成一个因数,首先应用:因数=积÷另一个因数方法来解(最关键是把括号看成一个整体,还把它看成一个什么数)(2.8+ⅹ)×2=10.4解:2.8+ⅹ=10.4÷22.8+ⅹ=5.2ⅹ=5.2-2.8ⅹ=2.4练习9题:2(ⅹ-2.6)=85(ⅹ+1.5)=17.5(ⅹ-3)÷2=7.5(ⅹ-3)÷6=6.32+(ⅹ-2.6)=85+(ⅹ+1.5)=17.5(ⅹ-6.2)-8=41.6(ⅹ-3)-2=7.5(ⅹ-3)÷0.2=7.5。

苏教版五年级下册简易方程知识点梳理及错题好题经典集锦第一单元:简易方程知识点梳理一、字母表示数1.在含有字母的式子里,字母中间的乘号可以记作“·”,也可以省略不写。
加号、减号、除号以及数与数之间的乘号不能省略。
2.a×a可以写作a·a(或a²),a²读作a的平方,表示两个a相乘。
XXX表示a+a。
二、方程的定义及解方程1.方程:含有未知数的等式称为方程。
2.方程的解:使方程左右两边相等的未知数的值,叫做方程的解。
3.解方程:求方程的解的过程叫做解方程。
4.解方程原理:天平平衡。
等式左右两边同时加、减、乘、除相同的数(除外),等式依然成立。
方程两边同时加、减、乘、除一个不等于的数,左右两边仍然相等。
5.解方程需要注意:1)一定要写‘解’字。
2)等号要对齐。
3)两边乘除相同数的时候,这个数不要省略。
三、10个数量关系式:加法:和=加数+加数一个加数=和-另一个加数减法:差=被减数-减数被减数=差+减数减数=被减数-差乘法:积=因数×因数一个因数=积÷另一个因数除法:商=被除数÷除数被除数=商×除数除数=被除数÷商四、方程和等式的关系:含有未知数的等式叫做方程,所有的方程都是等式,但等式不一定都是方程。
五、方程的检验过程:把X=……带入原方程左边=…右边=左边=右边所以X=……是原方程的解练:1.排球队共有a人,女队员有7人,男队员有(a-7)人。
2.1千克大米的价钱是1.50元,买x千克大米应付(1.5x)元。
3.甲数比乙数的3倍还多a,甲数是x,乙数是(x-a÷3);如果乙数是x,那么甲数是(x+a÷3)。
4.省略乘号,写出下面的式子。
3a,9x,4a,5y,3ax5.方程0.6x=3的解是(5)。
6.ac+bc=(a+b)×c7.a与b的和的5倍是(5a+5b)。
8.梯形面积计算公式用字母表示是((a+b)×h÷2),三角形面积计算公式用字母表示是(ah÷2)。

五年级下册数学知识整理第一单元简易方程简易方程是数学中的一种基本概念,用于表示未知数与已知数之间的关系。
在五年级下册数学中,学生将进一步学习和掌握简易方程的解法和应用。
一、简易方程的基本概念1. 未知数:在简易方程中,用字母(通常是x)表示未知数,代表一个待求的数。
2. 已知数:在简易方程中,已知的数值称为已知数,可以直接使用。
3. 等号:简易方程中,未知数和已知数之间的关系通过等号表达,即左右两边的值相等。
二、简易方程的解法1. 逆运算法:根据简易方程的等号两边的关系,使用逆运算逐步消去已知数,求得未知数的值。
2. 一次转移法:通过一次变换,使得方程中的未知数系数为1,然后求得未知数的值。
3. 正确性验证:将求得的未知数值代入原方程,验证等号两边是否相等,以验证解的正确性。
三、简易方程的应用1. 推理和问题解决:通过简易方程的应用,培养学生的逻辑思维能力和问题解决能力。
2. 实际问题的建立和解决:通过将实际问题转化为简易方程,帮助学生理解和解决实际问题。
四、简易方程的例题1. 例题1:某个数与12的差是5,求这个数。
解法:设这个数为x,根据题意列出方程:x - 12 = 5。
使用逆运算法,将已知数12移到右边,得到x = 17。
2. 例题2:某个数的三倍加2等于20,求这个数。
解法:设这个数为x,根据题意列出方程:3x + 2 = 20。
使用一次转移法,将未知数系数变为1,得到x = (20 - 2) / 3 = 6。
3. 例题3:某个数的2倍减去3等于7,求这个数。
解法:设这个数为x,根据题意列出方程:2x - 3 = 7。
使用逆运算法,将已知数3移到右边,得到2x = 7 + 3 = 10。
然后将方程两边同除以2,得到x = 5。
五、简易方程的拓展1. 二元一次方程:两个未知数的方程,例如:2x + y = 10。
2. 多元线性方程:多个未知数的方程,例如:2x + 3y + z = 20。


数学五年级下册苏教版第一单元:简易方程1. 简易方程概述在数学中,简易方程是一种常见的代数问题,它通常用来描述未知数和已知数之间的关系。
在五年级下册苏教版教材中,第一单元就是关于简易方程的学习。
学生在这一单元中将学习如何使用简易方程解决实际生活中的问题。
2. 理解简易方程简易方程可以被表示为一个等式,其中包含了一个未知数和一些已知数以及一些运算符号。
在简易方程"2x + 5 = 11"中,未知数为"x",已知数为"2"、"5"和"11",而运算符号为"+"和"="。
学生需要理解如何根据已知数和运算符号来求解未知数的值。
3. 解决简易方程的方法在五年级下册苏教版教材中,学生将学习如何使用逆运算来解决简易方程。
逆运算是指与某一运算相反的运算,例如加法的逆运算是减法,乘法的逆运算是除法。
通过应用逆运算,学生可以逐步求解简易方程中的未知数。
4. 实际问题的应用在学习简易方程的过程中,教材中也会给出一些实际生活中的问题,让学生应用所学知识来解决这些问题。
一个花坛里有5棵小树,比大树少2棵,那么花园里有多少棵大树。
通过建立简易方程,学生可以找到大树的数量,并且理解数学知识在实际生活中的应用。
5. 练习题和解答在每个教材单元的末尾,一般都会有练习题和解答,在学习简易方程的单元中也不例外。
这些练习题旨在帮助学生巩固所学知识,并通过实际练习提高解决简易方程的能力。
总结简易方程作为数学中的一种代数问题,对于五年级学生来说是一个重要的学习内容。
通过学习简易方程,学生可以培养逻辑思维能力和数学解决问题的能力,在实际生活中也能更好地理解并应用数学知识。
五年级下册苏教版的简易方程单元,不仅仅是纸上的知识,更是对学生综合能力的培养和提高的一次重要的学习机会。
通过五年级下册苏教版的简易方程单元学习,学生们可以逐步掌握解决实际问题的数学方法和技巧,同时也培养了他们的逻辑思维能力和数学解决问题的能力。

苏教版数学五年级下册知识点整理第一单元 简易方程一、知识点梳理(一)方程1.等式的意义:表示相等关系的式子叫做等式。
2.方程的意义:像x +50=150、2x =200 这样含有未知数的等式是方程。
3.方程与等式的关系:方程是等式,但等式不一定是方程,它们之间可以用右图表示:4.方程必须满足的条件:(1)必须是等式。
(2)必须含有未知数。
(二)解方程5.方程的解和解方程:使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
6.等式的性质:(1)等式的两边加上或减去同一个数,所得结果仍然是等式。
(即左右两边仍然相等)(2)等式的两边乘或除以同一个不是0的数,所得结果仍然是等式。
7.四则运算各部分的关系:一个加数=和-另一个加数 减数=被减数-差 被减数=减数+差一个因数=积÷另一个因数 除数=被除数÷商 被除数=商×除数8.解方程的常用方法:(1)等式的性质 (2)四则运算各部分的关系 (3)移项9.方程的检验:将方程的解代入原方程看方程左右两边是否相等。
(三)列方程解决问题10.一般步骤:(1)审:认真审题,理解题意,寻找等量关系。
(2)设:设未知数。
(一般设所求的未知数为x ,如果未知数有几个,可以设其中一个,然后根据关系表示其他未知数;也可以间接设某个量为x ,再通过这个量去求未知数。
)(3)列:根据题中所设的未知数和已知条件,按照等量关系式列出方程(4)解:求出所列方程的解。
(5)验:检验方程的解是否正确,检验方程的解是否符合题意。
(6)答:回答题目所问,写出答句。
11.注意点:(1)找到等量关系是列方程解决问题的关键。
(2)列方程解决问题时一般不把未知数x 单独放在一边。
(3)设未知数x 时要在后面写上单位名称,求出的x 的值不带单位名称。
等式 方程(四)其他相关知识点12.连续的自然数(或连续的奇数,连续的偶数)的和:3个连续自然数(或连续奇数、偶数)的和等于中间的一个数的3倍。
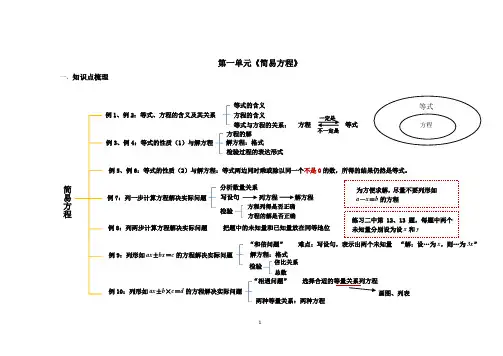
第一单元《简易方程》一、知识点梳理简易方程例1、例2:等式、方程的含义及其关系例3、例4:等式的性质(1)与解方程例5、例6:等式的性质(2)与解方程:等式两边同时乘或除以同一个不是0的数,所得的结果仍然是等式。
例7:列一步计算方程解决实际问题例8:列两步计算方程解决实际问题例9:列形如ax±bx=c的方程解决实际问题例10:列形如ax±b×c=d的方程解决实际问题等式的含义方程的含义等式与方程的关系:方程等式一定是不一定是方程的解解方程:格式检验过程的表达形式分析数量关系写设句列方程解方程检验方程列得是否正确方程的解是否正确把题中的未知量和已知量放在同等地位“和倍问题”难点:写设句,表示出两个未知量“解:设...为x,则 (3x)解方程:格式检验倍比关系总数为方便求解,尽量不要列形如a-x=b的方程“相遇问题”选择合适的等量关系列方程两种等量关系:两种方程画图、列表练习二中第12、13题,每题中两个未知量分别设为设x和y方程等式1二、教学注意事项1.方程的定义含有未知数的等式是方程。
2.等式的定义含有等号的式子叫做等式。
3.等式和方程的关系等式和方程的关系可以用下图表示:4.等式的性质(1)等式的两边同时加上或减去同一个数,所得结果仍然是等式。
(2)等式两边同时乘或除以同一个不是0的数,所得结果仍然是等式。
5.方程的解使方程左右两边相等的未知数的值叫作方程的解,求方程的解的过程叫作解方程。
方程的检验过程:把x=代入原方程,左边= ,左边=右边,所以x= 是原方程的解。
6.列方程解应用题的思路:(1)审题并弄懂题目的已知条件和所求问题。
(2)理清题目的等量关系。
(3)设未知数,一般是问什么就设什么为x。
(4)根据等量关系列方程。
(5)解方程。
(6)检验。
(7)作答。
三、典型试题一条公路长390米。
甲乙两支施工队同时从公路的两端往中间铺柏油,甲队的施工速度是乙队的1.5倍,6天后这条公路全部铺完,乙队每天铺柏油路多少米?思路解析:设乙队每天铺x米,则甲队每天能铺1.5x米,两队一天共可铺(1.5x+x)米,6天后这条公路全部铺完,已知公路全长390米,由此可得出方程。

完整版)苏教版五年级下册数学知识点总结苏教版五年级下册数学知识点总结第一单元:简易方程等式是表示相等关系的式子,含有未知数的等式是方程。
等式的性质有两个:等式两边同时加上或减去同一个数,所得结果仍然是等式;等式两边同时乘或除以同一个不等于的数,所得的结果任然是等式。
使方程左右两边相等的未知数的值叫做方程的解,求方程中未知数的过程叫做解方程。
解方程时常用的关系式有:一个加数=和-另一个加数,一个因数=积÷另一个因数,减数=被减数-差,被减数=减数+差,除数=被除数÷商,被除数=商×除数。
对于方程60-4X=20,解4X=60-20,得到X=10,检验后得知X=10是原方程的解。
第二单元:折线统计图复式折线统计图不仅能看出数量的多少和数量增减变化的情况,而且便于这两组相关数据进行比较。
作复式折线统计图的步骤包括:写标题和统计时间,注明图例,分别描点标数,实线和虚线的区分(画线用直尺)。
注意先画表示实线的统计图,再画虚线统计图,不能同时描点画线,以免混淆。
第三单元:因数和倍数几个非零自然数相乘,每个自然数都叫它们积的因数,积是这几个自然数的倍数。
一个数最小的因数是1,最大的因数是它本身,一个数因数的个数是有限的。
找因数的方法是成对的找。
1、一个分数由分子和分母组成,表示被分成若干份中的一份。
2、分数的大小关系可以通过比较它们的分子和分母的大小关系来确定。
3、分数的化简是指将分子和分母同时除以它们的最大公因数,使得分数变为最简形式。
4、分数的加减法需要先找到它们的公共分母,然后将分子进行加减,再将结果化简为最简形式。
5、分数的乘法是将分子和分母分别相乘,然后将结果化简为最简形式。
6、分数的除法是将除数的分子和被除数的分母相乘,除数的分母和被除数的分子相乘,然后将结果化简为最简形式。
7、分数的倒数是指分子和分母互换位置后得到的新分数。
8、分数的真分数是指分子小于分母的分数,假分数是指分子大于等于分母的分数,带分数是指由整数和真分数组成的分数形式。

第一单元:简易方程一、概述在学习数学的过程中,简易方程是一个非常重要的概念。
它不仅在数学中具有重要的地位,而且在日常生活中也有着广泛的应用。
通过学习简易方程,孩子们可以培养逻辑思维能力和解决问题的能力。
本文将以苏教版五年级下册数学第一单元为基础,探讨简易方程的相关知识,帮助孩子们更好地理解和掌握这一概念。
二、什么是简易方程简易方程指的是具有一个未知数的等式,通过这个等式可以求出未知数的数值。
在简易方程中,通常包括已知数、运算符号和未知数。
孩子们可以通过简易方程来解决一些实际问题,例如找出一个数的两倍是多少,或者一个数加上5等于10。
三、简易方程的表示方法1. 一元一次方程的表示方法一元一次方程是指只含有一个未知数和该未知数的一次幂的方程。
2x + 3 = 7就是一个一元一次方程。
在解一元一次方程时,通常需要用到加减消去、乘除消去等方法,将未知数的系数化为1,最终求出未知数的数值。
2. 用字母表示未知数在表示简易方程时,通常会用字母代表未知数。
用x代表一个数,那么2x + 3 = 7就表示这个数的两倍加3等于7。
通过这种表示方法,可以更好地理解和解决简易方程。
四、解简易方程的方法1. 加减消去法加减消去法是解简易方程的基本方法之一。
通过加减消去法,可以将方程中的未知数系数化为1,从而求出未知数的数值。
以2x + 3 = 7为例,通过减去3和再除以2的操作,可以求出未知数x的数值为2。
2. 乘除消去法乘除消去法也是解简易方程的常用方法之一。
通过乘除消去法,可以将方程中的未知数系数化为1,从而求出未知数的数值。
以2x - 4 = 8为例,通过先加上4再除以2的操作,可以求出未知数x的数值为6。
五、简易方程的应用1. 解决实际问题简易方程在解决实际问题时具有重要的应用价值。
通过简易方程可以求解一些关于数量关系的问题,帮助孩子们更好地理解和应用数学知识。
2. 培养逻辑思维能力通过学习简易方程,孩子们可以培养逻辑思维能力和解决问题的能力。
苏教版五年级下册。
第1单元。
简易方程知识点+重难点提升第一单元简易方程(知识点+重难点分析)1.等式表示相等关系,含有未知数的等式称为方程。
2.方程是一种等式,但等式不一定是方程。
3.等式有两个重要的性质:加减同一个数和乘除同一个非零数不改变等式的结果。
4.解方程是求使方程左右两边相等的未知数的值,解方程时常用的四则运算关系式包括加减乘除运算。
5.解方程的步骤包括写解、上下对齐、利用等式的性质解方程、检验和写答句。
6.列方程解应用题的思路包括审题、找等量关系、设未知数、列方程、解方程、检验和写答句。
7.找等量关系的方法可以根据条件想数量间的相等关系、根据计算公式确定等量关系或者画出线段图找等量关系。
重难点分类解析:类型一:利用等式的性质解方程这种类型的方程解法是利用等式的性质,通过加减乘除同一个数来解方程。
需要注意的是,解完方程后要进行检验,确保所得结果正确。
类型二:用形如ax+b=c的方程解决实际问题这种类型的方程需要根据实际问题设定未知量,并根据已知条件列出方程,然后解方程求解未知量。
需要注意的是,这种类型的方程可能会有多个未知量,需要设定不同的未知量来求解。
反馈练:一个水池分为深、浅两部分,深部分的水是浅部分水的3倍。
如果从深部分取出20升水放到浅部分,这时两部分水的水量正好相等。
原来深、浅两部分各有多少升水?例题2:甲、乙两人同时从A、B两地出发,相向而行,中途相遇后,甲车行驶的路程是乙车行驶路程的1.5倍。
如果两车相遇后,甲车再行驶10千米,乙车再行驶20千米。
这时两车行驶的路程相等。
A、B两地相距多少千米?点拨:这是一道稍复杂的差倍问题,需要先求出两车相遇时的路程差,再根据题意列方程求解。
反馈练:XXX和XXX同时从A、B两地出发,相向而行,中途相遇后,XXX行驶的路程是XXX行驶路程的2倍。
如果两人相遇后,XXX再行驶30千米,XXX再行驶20千米。
这时两人行驶的路程相等。
A、B两地相距多少千米?1.两袋面粉,原来甲袋的质量是乙袋的3倍,现从甲袋中取出34千克,则两袋面粉同样重。
小学数学苏教版-五年级下-第一单元-《简易方程》一、知识点(一)方程的定义及性质1.定义:含有未知数的等式是方程。
2.性质:(1)等式两边同时加上或减去同一个数,所得结果仍然是等式;(2)等式两边同时乘或除以同一个不是0的数,所得结果仍然是等式;3.使方程左右两边相等的未知数的值叫做方程的解,求方程的解的过程叫做解方程。
(二)列方程需要注意的问题列方程解决实际问题:(1)先弄清题意,找出未知量,并用字母表示;(2)要根据题中数量之间的相等关系列方程;(3)求出答案后,还要检验结果是否正确;(4)应用学过的公式、数量关系式或者画图,可以帮助我们寻找等量关系。
二、练习题(一)选择题1.下面式子中,()是方程.A.x+3B.4÷5=0.8C.0.8y+1=7D.10-x>22.下面各式中,()不是方程.A.3x+5x+1=8+1B.2.8+5x=12.8C.3.4x=0D.2x+4<243.a-b=4,7-x=5,5x>6,7y=35,67+a=77这几个式子中有()个方程.A.2B.3C.44.小亮比小强大2岁,比小花小4岁,如果小强是m岁,小花是()岁.A.m-2B.m+2C.m+4D.m+65.爸爸今年x岁,比舅舅大a岁,舅舅今年()岁.A.x+a B.x-a C.a-x6.与方程3x+8=68的解相同的是()A.12x=360B.8+2x=68C.15x=320-x7.方程3x=36的解与下面()的解相同.A.x+12=12B.12÷x=1C.2x+3=248.比x的3倍多1的数是4,列方程是()A.3x-1=4B.3-x=4C.3x+1=49.下面的x的值中,()是方程3x+5=20的解A.x=5B.x=6C.x=710.根据x+4.5=9判断下面()成立.A.x+4.5-5=9+4.5B.(x+4.5)×2=9×3 C.x+4.5-4.5=9-4.5(二)填空题11.一本书有A页,小明每天看18页,看了B天,还剩下页没有看.12.甲数是a,比乙数多5,乙数是.13.小明今年a岁,爸爸的年龄比他的3倍大b岁,爸爸今年岁.14.哪些是等式,哪些是方程.(填写序号)①x+5=40②20-10x③7a=14④160÷8=20⑤9x>80⑥5a⑦(n-2)×180=540等式有方程有.15.已知0.6x+8=20,那么5x-9=.16.按要求在横线上列方程.(1)5与b的和是24.(2)3个y的和是60.17.填上适当的数,使每个方程的解都是x=10x+=91x-=8.9x=5.1x÷=4(三)计算18.直接写出计算结果.x×3=3a+7a= 2.3t-1.3t=x+5.7x=m×m=0.84-0.4=9.6÷0.6=12.5×80=8.48÷0.8=1÷0.01×9.2=19.解方程.3x-48=72 5.9x-2.4x=7x÷2.6=0.84x-6=284x-2x=482x÷9=2520.三个连续整数的和是63,最小数为a,求这三个数.(列方程解答)三、答案及解析1.【答案】C【解析】A、x+3,只是含有未知数的式子,不是等式,不是方程;B、4÷5=0.8,只是等式,不含有未知数,不是方程;C、0.8y+1=7,既含有未知数又是等式,具备了方程的条件,因此是方程;D、10-x>2,虽然含有未知数,但它是不等式,也不是方程.2.【答案】D【解析】A、3x+5x+1=8+1,既含有未知数又是等式,具备方程的条件,因此是方程;B、2.8+5x=12.8,既含有未知数又是等式,具备方程的条件,因此是方程;C、3.4x=0,既含有未知数又是等式,具备方程的条件,因此是方程;D、2x+4<24,只是含有未知数的式子,不是等式,所以不是方程.3.【答案】C【解析】这几个式子中方程有:a-b=4,7-x=5,7y=35,67+a=77,共4个;故选:C.4.【答案】D【解析】m+2+4=m+6(岁).答:小花是(m+6)岁.故选:D.5.【答案】B【解析】舅舅比爸爸小a岁,所以用爸爸的年龄减a就是舅舅的年龄.舅舅今年(x-a)岁.6.【答案】C【解析】3x+8=68解:3x+8-8=68-83x=603x÷3=60÷3x=20A.把x=20代入12x=360,左边=12×20=240,右边=360,左边≠右边,所以它们的解不同;B.把x=20代入8+2x=68,左边=8+2×20=8+40=48,右边=68,左边≠右边,所以它们的解不同;C.把x=20代入15x=320-x,左边=15×20=300,右边=320-20=300,左边=右边,所以它们的解相同7.【答案】B【解析】3x=36解:3x÷3=36÷3x=12A.把x=12代入x+12=12,左边=12+12=24,右边=12,左边≠右边,所以它们的解不同;B.把x=12代入12÷x=1,左边=12÷12=1,右边=1,左边=右边,所以它们的解不同;C.把x=12代入2x+3=24,左边=2×12+3=27,右边=24,左边≠右边,所以它们的解不同。
简易方程知识盘点知识点1:等式和方程的意义1、表示相等关系的式子叫做等式。
从形式是看,含有“=”的式子就是等式。
2、含有未知数的等式是方程。
知识点2:等式和方程的关系方程一定是等式;等式不一定是方程。
知识点3:等式的性质① 等式两边同时加上或减去同一个数,所得结果仍然是等式。
② 等式两边同时乘或除以同一个不等于0的数,所得的结果仍然是等式。
知识点4:解方程1、方程的解:使方程左右两边相等的未知数的值。
2、解方程:求方程中未知数的过程。
3、用等式的性质可以直接解形如x ±a=b 、a x =b 、x ÷a=b 的方程。
4、用等式的性质解形如a x ±b x =c (a±b≠0)的方程的具体解法及书写格式如下:a x ±b x =c解: (a ±b )x =c(a ±b )x ÷(a ±b )=c ÷(a ±b )x =c÷(a ±b )5、解形如a x +ab =c (a≠0)的方程的方法。
(1)解形如a x +ab =c 的方程时,把ax 看作一个整体,先求a x 的值,再求x 的值。
(2)解形如a (x +b )=c 的方程时,把小括号内的x +b 看作一个整体,先求x +b 的值,再求x 的值。
⭐注意 方程具备的特征:①就含有未知数;②等式知识点5:用方程解决实际问题 1、列方程解应用题的思路:①审题并弄懂题目的已知条件和所求问题, ②理清题目的等量关系,③设未知数,一般是把所求的数用x 表示, ④根据等量关系列出方程, ⑤解方程, ⑥检验, ⑦作答。
2、已知数量甲比数量乙的几倍多(或少)几和数量甲,求数量乙的实际问题, 可设数量乙为x ,根据数量乙×倍数±几=数量甲,列出形如a x ±b=c 的方程 进行解答。
3、解决涉及两个未知量的问题时,一般设其中的一个未知量为x (通常设标准量 为x ),另一个未知量用含有x 的式子表示,然后根据等量关系式列方程求解。
第一单元简易方程
1、表示相等关系的式子叫做等式。
2、含有未知数的等式是方程。
3、方程一定是等式;等式不一定是方程。
等式>方程
4、等式两边同时加上或减去同一个数,所得结果仍然是等式。
这是等式的性质。
5、使方程左右两边相等的未知数的值叫做方程的解。
6、求方程中未知数的过程,叫做解方程。
7、检验格式:60-4X=20 解4X=60-20 4 X=40 X=10 ①检验:把X=10代入原方程,
左边=60-4×10=20, 右边=20, 左边=右边,所以,X=10是
原方程的解. ②检验:方程左边=60-4×10=20 =方程右边所以,
X=10是方程的解
8、解方程时常用的关系式:一个加数=和-另一个加数
减数=被减数-差被减数=减数+差一个因数=积÷另一个因数
除数=被除数÷商被除数=商×除数
9、五个连续的自然数(或连续的奇数,连续的偶数)的和,等于
中间的一个数的5倍。
奇数个连续的自然数(或连续的奇数,连
续的偶数)的和÷个数=中间数
10、 10、4个连续的自然数(或连续的奇数,连续的偶数)的和,等于中间两个数或首尾两个数的和×个数÷2(高斯求和公式) 11、列方程解应用题的思路:A、审题并弄懂题目的已知条件和所求问题。
B、理清题目的等量关系。
C、设未知数,一般是把所求的数用X表示。
D、根据等量关系列出方程E、解方程F、检验G、作答。
注意:解完方程,要养成检验的好习惯。