五年级数学上册《简易方程》知识点汇总

第五章五年级上册数学第五单元简易方程【知识回顾】用字母表示数（1）用字母表示数量关系、运算定律和计算公式知识点一、用字母表示数用含有字母的式子表示数量关系时,如果出现字母与数相乘时,要省略乘号时,一般把数写在字母前面。

知识点二、用字母表示运算定律和计算公式（1）乘法交换律：a×b＝b×a → a·b＝b·a 或ab＝ba乘法结合律：（a×b）×c＝a×（b×c）→（a·b）·c＝a·（b·c）或（ab）c＝a（bc）乘法分配律：（a＋b）×c ＝a×c＋b×c→（a＋b）·c ＝a·c＋b·c或（a＋b）·c ＝ac＋bc（2）用S表示面积,用C表示周长。

1）如果用a表示正方形的边长 , 那么这个正方形的周长：C =a·4=4a（省略乘号时,一般把数写在字母前面）这个正方形的面积：S =a·a=（读作：a的平方,表示2个a相乘）2）如果用a表示长方形的长, b表示宽,那么这个长方形的周长：C =（a+b）·2=2（a+b）这个长方形的面积：S = a·b=ab【典题解析】例：（1）读出下面各式,并说明表示的意义．（2）把下面各式写成一个数的平方的形式．5×5（3）省略乘号,写出下面各式．（4）根据运算定律在□填上适当的字母或数．（□＋□）＋□□·（□·□）（5）如果用表示长方形的长,表示宽,那么这个长方形的面积 _____________________,这个长方形的周长 _____________________．【随堂练习】一、我会省略乘号写出下面各式。

ａ×12＝ｂ×ｂ＝ａ×ｂ＝ｘ×ｙ×7＝5×ｘ＝2×ｃ×ｃ＝7ｘ×5＝2×ａ×ｂ＝二、我会判断。

简易方程是指只含有一个未知数的方程，通常以字母x表示未知数，如：2x+3=7、在这个方程中，未知数x的值为多少，是需要我们求解的。

五年级学生会学习如何通过逆向思维推导未知数的值，从而解决简易方程问题。

下面是五年级数学简易方程的主要知识点：1.方程的定义：方程是由等号连接的两个代数式组成的数学式子。

例如：2x+3=72.未知数：在方程中，未知数是我们要求解的对象，通常用字母表示，如x、y 等。

3.等式：方程中等号左右两侧的代数式相等，表示方程的基本关系。

如2x+3=74.解方程的基本方法：解方程的目的是求出未知数的值。

通常需要通过“逆向运算”的方法，逐步将未知数“从一边移到另一边”，直到得到未知数的具体值。

5.逆向运算：在解方程时，当方程中有一项与未知数相乘（或相除）时，可以通过与这项相反的运算，将未知数的系数化为1、例如方程2x=8，可以通过除以2的运算将方程转化为x=46.两侧相等性质：方程中的等号两侧进行相同的运算，结果仍然相等，即方程仍然成立。

例如方程2x=8，如果两侧同时除以2，则得到x=4，这个方程的解与原方程相等。

7.减去常数、乘以常数：方程中可以进行减去常数和乘以常数的运算，不会改变方程的解。

例如方程2x-3=7，如果两侧同时加上3，则得到2x=10，这个方程的解与原方程相等。

8.联立方程：联立方程是指同时解多个方程的问题。

对于两个方程，可以利用消元法或代入法来求解。

9.检验答案：求解方程之后，需要对解进行检验以确认答案的正确性。

将解代入原方程中，检验等号两侧是否相等。

数学五年级上的简易方程是指具有一个未知数的方程，解方程的目的是确定未知数的值。

在五年级上，主要学习了一元一次方程的解法和应用。

接下来，我将对五年级上的简易方程知识点进行总结。

一、一元一次方程一元一次方程指的是只有一个未知数，并且未知数的最高次数为一的方程。

一元一次方程的一般形式如下：ax + b = 0其中，a和b为已知数，x为未知数。

二、解一元一次方程方法与步骤解一元一次方程的方法主要有逆运算法、解方程三大性质法以及方程图法。

下面是逆运算法的步骤：1.对方程两边采取相反的运算，使含有未知数的项变为零；2.化简式子，得到未知数的值。

三、逆运算法逆运算法是解一元一次方程最常用的方法，逆运算指的是对方程两边采取相反的运算。

1.加减法逆运算：对于a+b=c这个方程，如果想求出a的值，只需要对两边同时进行减法运算即可，即a=c-b。

2.乘除法逆运算：对于a*b=c这个方程，如果想求出a的值，只需要对两边同时进行除法运算即可，即a=c/b。

四、解一元一次方程的步骤1.对方程进行加减法逆运算，使含有未知数的项变为零；2.化简式子，得到未知数的值。

五、解方程三大性质法解方程三大性质法是指解一元一次方程时使用的三个性质：等式两边交换位置后仍然成立、等式两边同时加上或减去相同的数后仍然成立、等式两边同时乘以或除以相同的非零数后仍然成立。

1.等式两边交换位置后仍然成立的性质：例如，对于方程a+b=c，如果将a和b交换位置，得到b+a=c，仍然成立。

2.等式两边同时加上或减去相同的数后仍然成立的性质：例如，对于方程a+b=c，如果两边同时加上d，得到a+b+d=c+d，仍然成立。

3.等式两边同时乘以或除以相同的非零数后仍然成立的性质：例如，对于方程a+b=c，如果两边同时乘以d，得到a*d+b*d=c*d，仍然成立。

六、方程图法方程图法是通过绘制方程的解所在的点在平面直角坐标系中的图形，来求解一元一次方程。

首先，将方程的解表示为坐标图上的点，再根据点的特征绘制图形。

五年级上册解简易方程难点归纳一、一步方程只有一步计算的方程，直接逆运算除未知数外的部分.x—6=7 解：x-6+6=7+6x=133x=18解：3x÷3=18÷3x=6x÷4=5解：x÷4×4=5×4x=20难点：当未知数出现在减数和除数时，要先逆运算含未知数的部分.16—x=9 解：16—x+x=9+xx+9=16x+9—9=16—9x=724÷x=4 解：24÷x×x=4×x4x=244x÷4=24÷4x=6二、两步方程两步方程中，若是只有同级运算，也可以先计算，后当做一步方程求解.注意要“带符号移动”，增添括号时还要注意符号的变化.10+x—6=20 解：x+(10—6)=20x+4=20x+4—4=20—4x=16x÷4×8=9.6 解：x×(8÷4)=9.62x=9.62x÷2=9.6÷2x=4.8如果含有两级运算，就“逆着运算顺序”同时变化，如含有未知数的一边是“先乘后减”，则先逆运算减法（即两边同加），再逆运算乘法（即两边同时除以），依此类推.x÷4+6=7.8 解：x÷4+6—6=7.8-6x÷4=1.8x÷4×4=1.8×4x=7.23(x-6)=6.6 解：3(x-6)÷3=6.6÷3x—6=2.2x—6+6=2.2+6x=8.2难点：当未知数出现在减数和除数时，要先把含有未知数的部分看作一个整体（可以看成是一个新的未知数），就相当于简化成了一步方程.6+64÷x=10 解：6+64÷x—6=10—664÷x=464÷x×x=4×x4x=644x÷4=64÷4x=165(7.2—x)=6 解：5(7.2—x)÷5=6÷57.2—x=1.27.2—x+x=1.2+xx+1.2=7.2x+1.2—1.2=7.2—1.2x=6三、三步方程（1）应用乘法分配律，共同因数是已知数的具有乘法分配律的形式，即两个有共同因数的乘积（或具有相同除数的除法式子）相加或相减，而共同因数（或除数）是已知数的，既可以逆用乘法分配律提取共同因数而将其简化为两步方程，也可以直接算出已知部分而化简.2.4x+2.4×8=36解：2.4(x+8)=362.4(x+8)÷2.4=36÷2.4x+8=15x+8-8=15-8x=7 或2.4x+2.4×8=36解：2.4x+19.2=362.4x+19.2-19.2=36—19.22.4x=16.82.4x÷2.4=16.8÷2.4x=7通过比较可以看出，一般来说提取共同因数的方法确实计算量要少一些，不容易算错.（2）应用乘法分配律，共同因数是未知数的具有乘法分配律的形式，即两个有共同因数的乘积（或具有相同除数的除法式子）相加或相减，而共同因数（或除数）是未知数的，只能逆用乘法分配律提取共同因数而将其简化为两步方程.2.4x+3.6x=36解：(2.4+3.6)x=366x=366x÷6=36÷6x=68÷x+12÷x=4 解：(8+12)÷x=420÷x=420÷x×x=4×x4x=204x÷4=20÷4 x=5。

五年级上册第五单元简易方程知识点及基本题型解析1、在含有字母的式子里，字母中间的乘号可以记作“·”，也可以省略不写。

注：加号、减号除号以及数与数之间的乘号不能省略。

例1、省略乘号，写出下面各式。

a×3=(3a) 7×a×b=(7ab) b×3×a=(3ab)2、a×a可以写作a·a或a2读作a的平方。

注： 2a表示a+a ； a2表示a×a例2、7²=（7×7） x·x＝（x²）3、方程：含有未知数的等式称为方程。

例3、（1）4X-8=10（是）方程，（2）4X-8<10（不是）方程，（3）4+2=6（不是）方程。

解析：（1）有未知数，有等式是方程。

（2）有未知数，不是等式不是方程。

（3）没有未知数有等式不是方程。

4、使方程左右两边相等的未知数的值，叫做方程的解。

例4、（X=3）是方程4X-8=4的解。

5、求方程的解的过程叫做解方程。

6、解方程原理：天平平衡。

等式左右两边同时加、减、乘、除相同的数（0除外），等式依然成立。

例5、解下列方程.X+4.8=7.2 X-0.8=8解：X+4.8-4.8=7.2-4.8 解：X-0.8+0.8=8+0.8X=2.4 X=8.87、10个数量关系式：和=加数+加数；一个加数=和-两一个加数差=被减数-减数；被减数=差+减数；减数=被减数-差积=因数×因数；一个因数=积÷另一个因数商=被除数÷除数；被除数=商×除数；除数=被除数÷商例6、解方程：（1）2.5x-2.5=10 （2）1.4×6-3x=1.5解：2.5x-2.5+2.5=10+2.5 解：6.4-3x=1.52.5x=12.5 3x=6.4-1.52.5x÷2.5=12.5÷2.5 3x÷3=3.9÷3x=5 x=1.3（3）12.6x-4.6x-5=123 （4）3.6+(x-5)×1.2=18 解：（12.6-4.6）x-5=123 解：3.6+(x-5)×1.2-3.6=18-3.68x-5+5=123+5 (x-5)×1.2=14.48x=128 (x-5)×1.2÷1.2=14.4÷1.2X=16 x-5+5=12+5X=17 例7.、列方程解文字题：（1）一个数的5.8倍减去这个数本身，差是26.4，这个数是多少？解：设这个数是x。

小学五年级数学简易方程的知识点归纳数学方程是数学中常见的一个概念，它是一个等式，其中包含一个或多个未知数。

在小学五年级的数学学习中，学生开始接触简易方程的概念和解题方法。

本文将对小学五年级数学简易方程的知识点进行归纳。

一、方程的基本概念方程是由等号连接的两个代数式组成，其中至少包含一个未知数。

例如，下面的方程是一个简单的数学方程：2x + 3 = 9在这个方程中，未知数是x，左边的2x + 3是一个代数式，右边的9也是一个代数式。

二、方程的解解方程，就是要找到使得方程成立的未知数的值。

对于简易方程来说，解通常是一个特定的数。

在解方程时，我们必须使用逆运算来保持等式的平衡。

例如，对于上面的方程2x + 3 = 9，我们可以先减去3再除以2来解方程，即：2x + 3 - 3 = 9 - 32x = 62x ÷ 2 = 6 ÷ 2x = 3所以x=3是这个方程的解。

三、方程的变形及性质在解方程的过程中，我们经常需要进行方程的变形。

方程的变形即改变方程的形式，使得方程更易于求解。

常见的方程变形方法包括：1. 合并同类项：将方程中相同的项合并，以简化方程。

2. 移项：将方程中的项按照规则从一边移到另一边，以便合理组织方程形式。

3. 消元：通过适当的运算，使得方程中的某些项相互抵消，以简化方程。

四、常见的简易方程类型1. 一元一次方程：一元一次方程是最简单的方程类型，形式为ax +b = c，其中a、b、c都是已知的实数，且a不等于0。

例如：2x + 3 = 7解这个方程的步骤是：2x + 3 - 3 = 7 - 32x = 42x ÷ 2 = 4 ÷ 2x = 2所以，这个方程的解是x=2。

2. 带括号的一元一次方程：在一元一次方程中，有时方程中带有括号，解这类方程的关键是先去括号再进行求解。

例如：3(x + 2) = 15首先展开括号：3x + 6 = 15然后解方程：3x + 6 - 6 = 15 - 63x = 93x ÷ 3 = 9 ÷ 3x = 3因此，这个方程的解是x=3。

小学五年级上册数学《简易方程》知识点及练习题【#五年级# 导语】方程是指含有未知数的等式。

是表示两个数学式（如两个数、函数、量、运算）之间相等关系的一种等式，使等式成立的未知数的值称为“解”或“根”。

求方程的解的过程称为“解方程”。

简易方程是小学生应该掌握的必要知识之一。

为大家准备了以下内容，希望对大家有帮助。

【篇一】小学五年级上册数学《简易方程》知识点1、方程的意义含有未知数的等式，叫做方程。

2、方程和等式的关系3、方程的解和解方程的区别使方程左右两边相等的未知数的值，叫做方程的解。

求方程的解的过程叫做解方程。

4、列方程解应用题的一般步骤(1)弄清题意，找出未知数，并用表示。

(2)找出应用题中数量之间的相等关系，列方程。

(3)解方程。

(4)检验，写出答案。

5、数量关系式加数=和-另一个加数减数=被减数–差被减数=差+减数因数=积另一个因数除数=被除数商被除数=商除数【篇二】小学五年级上册数学《简易方程》练习题一、填空。

1、某厂计划每月用煤a吨，实际用煤b吨，每月节约用煤( )吨。

2、一本书100页，平均每页有a行，每行有b个字，那么，这本书一共有( )个字。

3、用字母表示长方形的周长公式（）4、根据运算定律写出：9n+5n=( + )n= a×0.8×0.125=(×)ab=ba运用（）定律。

5、实验小学六年级学生订阅《希望报》186份，比五年级少订a份。

186+a 表示（）6、一块长方形试验田有4.2公顷，它的长是420米，它的宽是（）米。

7、一个等腰三角形的周长是43厘米，底是19厘米，它的腰是（）。

8、甲乙两数的和是171.6，乙数的小数点向右移动一位，就等于甲数。

甲数是（）；乙数是（）。

二、判断题。

（对的打√，错的打×）1、含有未知数的算式叫做方程。

（）2、5x表示5个x相乘。

（）3、有三个连续自然数，如果中间一个是a,那么另外两个分别是a+1和a-1。

5简易方程
特别注意:
加号、减号、除号及数与
数之间的乘号不能省略。

提示:
2a与a2的区别:
2a表示a+a,a2表示a×a。

提示:
省略乘号时,一般把数字写
在字母的前面。

举例:x×6可以写成6x。

提示:
1×a省略乘号时,不能写成
1a,要写成a,这里的“1”我们要
省略不写。

温馨提示:
用含有字母的式子表示数
量关系,是加减关系时,如果后
面加单位,必须把这个含有字母
的式子用括号括起来。

注意:
方程必须满足的条件:必须
是等式,必须有未知数,二者缺
一不可。

易错点:
误认为含有未知数的式子
是方程。

举例:
3x-2>18是方程。

( )
正确解答:(✕)
提示:
等式的性质是解方程的重。

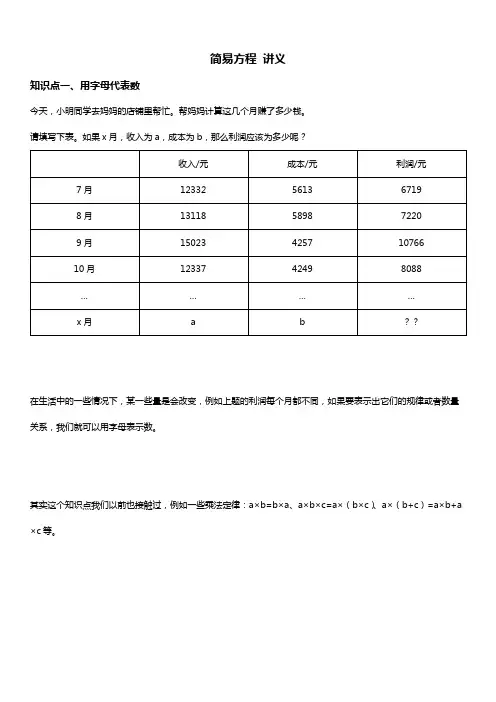
简易方程讲义知识点一、用字母代表数今天，小明同学去妈妈的店铺里帮忙。

帮妈妈计算这几个月赚了多少钱。

请填写下表。

如果x月，收入为a，成本为b，那么利润应该为多少呢？在生活中的一些情况下，某一些量是会改变，例如上题的利润每个月都不同，如果要表示出它们的规律或者数量关系，我们就可以用字母表示数。

其实这个知识点我们以前也接触过，例如一些乘法定律：a×b=b×a、a×b×c=a×（b×c）、a×（b+c）=a×b+a ×c等。

写法规范：1、在含有字母的式子中，字母与字母、数字与字母之间的乘号可以记为“.” ，也可以省略不写。

加号、减号、除号不能省略，数字与数字之间的乘号也不能省略。

例：2×a 可以写作2a ；a ×b 可以写作ab ；但2×3不能．．写作2.3，也不能．．写作23 。

2、如果字母前面的数字是1，则省略这个1。

例：1a 要写成a ；1x 要写成x 。

例1、根据下列要求列式。

（1）比x 的2倍少3的数。

（ ）（2）一列火车每小时行78千米，t 小时行多少千米? （ ）（3）李庄m 公顷的麦田，共收a 千克的小麦，平均每公顷产小麦多少千克? （ ） （4）a 与b 的差除以4的商。

（ ）（5）办公桌每张单价a 元，办公椅每把单价b 元，买m 套办公桌椅共付多少元? （ ）例2、3a+4a=（ ）；5a-3a=（ ）例3、如图所示，用含有字母的式子表示图中阴影部分的面积是（ ）；当b=20厘米，a=18厘米时，阴影部分的面积是（ ）。

例4、小明身高142厘米；比哥哥矮a 厘米；哥哥身高（ ）厘米。

例5、爸爸今年a 岁；比妈妈大3岁；表示妈妈明年岁数的式子是（ ）。

A 、a+3 B 、a-3 C 、a-3+1课堂练习１、a与b的和的9倍用式子表示为（）。

A、a+9bB、9a+bC、9(a+b)2、三个边长都是c厘米的正方形拼成一个长方形，这个长方形的周长是（）厘米。

一、方程的概念方程是一个含有未知数的等式。

方程的解就是能够使得方程成立的数值。

二、一步方程一步方程是指只需要一步运算就能求得未知数的方程。

例如：x+3=7，x-5=9三、积均差商1.积的意义：设一个数为x，另一个数为a，它们的积是m，那么可以用方程表示为：x*a=m。

2.均的意义：设一个数为x，另一个数为a，它们的均值是m，那么可以用方程表示为：(x+a)/2=m。

3.差的意义：设一个数为x，另一个数为a，它们的差是m，那么可以用方程表示为：，x-a，=m。

4.商的意义：设一个数为x，另一个数为a，它们的商是m，那么可以用方程表示为：x/a=m。

四、二步方程二步方程是指需要两步运算才能求得未知数的方程。

例如：2x+3=9，3x-5=7五、解一元一次方程的方法1.通过算式变形等式两边进行等式两边的运算，使得方程等式的形式更简单，进而求得未知数的值。

例如：x-5=10，可以通过加5得到x的值为152.通过倒运算等式两边进行倒运算，得出未知数的值。

例如：2x+3=9，可以通过减去3、除以2来得到x的值为3六、解二元一次方程的方法二元一次方程是含有两个未知数的方程，可以通过联立方程组的方法求解。

例如：x+y=5，2x+3y=10。

七、方程的解的判断在解一元方程或二元方程时，解的唯一性可以通过检验等式两边是否相等来判断。

综上所述，五年级数学简易方程的知识点包括方程的概念、一步方程、积均差商、二步方程、解一元一次方程的方法、解二元一次方程的方法以及方程的解的判断。

通过掌握这些知识点，学生可以解决简单的数学方程问题，提高数学解题的能力。

五年级数学上册简易方程讲义一、用字母表示数1、意义和作用：用字母表示数可以简明地表示数量关系、运算定律和计算公式，为研究和解决问题带来很多方便。

2、用字母表示常见的数量关系路程s, 速度v, 时间t总价a 单价b 数量c工作总量m 工作效率n 工作时间t3、用字母表示运算定律、性质、（1）运算定律(五大定律)：加法交换律：a+b＝b+a加法结合律：（a+b）+c＝a+（b+c）乘法交换律：ab=ba乘法结合律：（ab）c=a（bc）乘法分配律：a（b+c）＝ab+ac（2）运算性质（二大性质）：减法运算性质：a-（b+c）=a-b-c除法运算性质：（a＋b）÷c=a÷c＋b÷c（c≠0）4、用字母表示几何图形公式（1）平面图形（2）立体图形5、用字母表示数的规则1、数字与字母、字母和字母相乘时，乘号可以简写成“·“或省略不写。

数与数相乘，乘号不能省略。

2、当1和任何字母相乘时，“1”省略不写。

3、数字和字母相乘时，将数字写在字母前面。

省略乘号，写出下面各式5×b= c×a= x×6= t×9= 1×a=c×1= 12×a= 10×b= x×x=a³表示（）3a表示（）6、含有字母的式子及求值求含有字母的式子的值或利用公式求值，应注意书写格式。

5x+16x= 8b-3b= 10x-3x= Y+9y=10a-3a+5a= a+2a= 5c-4c= x+7x-4x=【练习】一、用含有字母的式子表示下面各题的数量关系◆ a 与8的和◆30减去b的差◆ c 的4倍◆ a 除以9的商◆比5.8多C的数◆比x的3倍多3◆5个a相加的和◆5个a相乘◆比a少20%二、在括号里填上适当的式子1、一天早晨的温度是X摄氏度，中午比早晨高8摄氏度，中午的温度（）摄氏度2、一个商场运来500辆自行车，总价是b元，单价是（）元3、食堂原计划每月烧煤a吨，实际节约b 吨，实际每月烧煤（）吨。

【篇一】小學五年級上冊數學《簡易方程》知識點1、方程的意義含有未知數的等式，叫做方程。

2、方程和等式的關係3、方程的解和解方程的區別使方程左右兩邊相等的未知數的值，叫做方程的解。

求方程的解的過程叫做解方程。

4、列方程解應用題的一般步驟(1)弄清題意，找出未知數，並用表示。

(2)找出應用題中數量之間的相等關係，列方程。

(3)解方程。

(4)檢驗，寫出答案。

5、數量關係式加數=和-另一個加數減數=被減數–差被減數=差+減數因數=積另一個因數除數=被除數商被除數=商除數【篇二】小學五年級上冊數學《簡易方程》練習題一、填空。

1、某廠計畫每月用煤a噸，實際用煤b噸，每月節約用煤( )噸。

2、一本書100頁，平均每頁有a行，每行有b個字，那麼，這本書一共有( )個字。

3、用字母表示長方形的周長公式（）4、根據運算定律寫出：9n+5n=( + )n= a×0.8×0.125=( ×)ab=ba運用（）定律。

5、實驗小學六年級學生訂閱《希望報》186份，比五年級少訂a份。

186+a表示（）6、一塊長方形試驗田有4.2公頃，它的長是420米，它的寬是（）米。

7、一個等腰三角形的周長是43釐米，底是19釐米，它的腰是（）。

8、甲乙兩數的和是171.6，乙數的小數點向右移動一位，就等於甲數。

甲數是（）；乙數是（）。

二、判斷題。

（對的打√，錯的打×）1、含有未知數的算式叫做方程。

（）2、5x表示5個x相乘。

（）3、有三個連續自然數，如果中間一個是a,那麼另外兩個分別是a+1和a-1。

（）4、一個三角形，底a縮小5倍，高h擴大5倍，面積就縮小10倍。

（）三、解下列方程。

3.5x=140 2x+5=40 15x+6x=1685x＋1.5=4.5 13.7—x=5.29 4.2×3—3x=5.1(寫出檢驗過程)四、列出方程並求方程的解。

（1）、一個數的5倍加上3.2，和是38.2，求這個數。

五年级简易方程笔记整理一、认识简易方程简易方程是一种数学表达式，通过将问题中的已知量和未知量用x和y来表示，从而形成一种简单明了的表达方式。

在五年级的学习中，我们需要掌握如何解一元一次的简易方程，以及如何利用简易方程解决实际问题。

二、简易方程的写法简易方程通常以ax+b=c的形式出现，其中a、b、c为已知量，x 为未知量。

在五年级的学习中，我们需要注意以下几点：1. 系数a可以表示一个常数，也可以表示一个比例关系；2. 方程中的常数项b必须为已知量；3. 方程的解需要满足方程的系数比例关系。

三、解简易方程解简易方程的过程就是通过移项、合并同类项等方法，将简易方程变形为x=k的形式，从而求出未知量的值。

在五年级的学习中，我们需要掌握以下几种解简易方程的方法：1. 直接代入法；2. 数字规律法；3. 换元法。

通过这些方法，我们可以快速准确地解简易方程，从而得到未知量的值。

四、简易方程的应用简易方程在生活中的应用非常广泛，例如行程问题、工程问题、价格问题等都涉及到简易方程。

在学习过程中，我们需要学会如何将实际问题转化为简易方程，并学会利用简易方程解决实际问题。

例如，在行程问题中，我们可以通过简易方程求出两地之间的距离、两人的速度等；在工程问题中，我们可以通过简易方程计算出完成一项工程需要的时间等。

这些问题的解决都需要我们熟练掌握简易方程的相关知识。

五、总结通过对五年级简易方程的学习，我们可以掌握简易方程的相关知识，包括如何写简易方程、如何解简易方程以及简易方程在生活中的应用等。

通过不断地练习和应用，我们可以提高自己的数学素养和解决问题的能力，为未来的学习和工作打下坚实的基础。

期末知识大串讲人教版数学五年级上册期末章节考点复习讲义第五单元简易方程知识点01：用字母表示数1. 用字母表示数量关系（1）可以用来表示一个数或表示数量关系；（2）字母与数字相乘时，把省略。

省略乘号时，一般把前面。

含有字母的式子中的不能省略。

2. 用字母表示运算定律和计算公式（1）在含有字母的式子里，只有之间的“×”才能简写成“.”或者省略不写。

注意：省略乘号后，数字必须写在字母的前边。

（2）应用公式求值解决问题的步骤：第一步：写出第二步：把字母表示的数值第三步：计算出结果，记住写单位3. 用字母表示复杂的数量关系（1）不同的式子可以表示相同的（2）将字母的代入含有字母的式子中,即可求得相应式子的值。

4. 化简含有字母的式子并代入数据求值计算含有字母的式子的时候，可以先运用运算定律将含有字母的式子进行。

知识点02：解简易方程1.方程的意义（1）方程的意义：是方程。

（2）方程必须具备的两个条件：一是；二含有。

2.方程一定是；但等式3. 所有的方程都是，但等式4.等式的性质等式的性质1：。

等式的性质2: 。

5.方程的解，叫做方程的解。

叫做解方程。

考点01：用字母表示数1．（2022秋•龙口市月考）静静今年10岁，妈妈比她大a岁，再过m年，妈妈比静静大（）岁。

A．10+a B．a C．m2．（2022春•遂平县期末）妈妈今年a岁，比笑笑年龄的3倍少5岁，笑笑今年（）岁。

A．3a﹣5 B．（a+5）÷3 C．a÷3﹣s3．（2022•阿荣旗）此图的面积可以表示为，也可以表示为，所以得到等式。

4．（2022春•铜山区期末）为营造温馨的书香氛围，五（1）班捐书x本，五（2）班捐书本数比五（1）班的2倍少12本，五（2）班捐书本，两班共捐书本。

5．（2022•阿荣旗）如果a＝b，那么a÷d＝b÷d。

（判断对错）6．（2022春•鄠邑区期末）阳阳今年a岁，妈妈的年龄是她的5倍，4年后妈妈的年龄是（a+4）×5岁。

五年级数学上册《简易方程》知识点汇总1、在含有字母的式子里，数字和字母中间的乘号，字母和字母之间的乘号，可以记作“·”，也可以省略不写。

加号、减号，除号以及数与数之间的乘号不能省略。

2、a×a可以写作a·a或a ，a 读作a的平方。

2a表示a+a3、方程：含有未知数的等式称为方程。

方程一定是等式，但等式不一定是方程。

使方程左右两边相等的未知数的值，叫做方程的解。

求方程的解的过程叫做解方程。

（解方程要先写“解”）方程的解是一个数；解方程是一个计算过程。

4、解方程的原理：（1）等式的基本性质等式左右两边同时加、减、乘、除相同的数（0除外），等式依然成立。

（2）10个数量关系式：加法：和=加数+加数一个加数=和-两一个加数减法：差=被减数-减数被减数=差+减数减数=被减数-差乘法：积=因数×因数一个因数=积÷另一个因数除法：商=被除数÷除数被除数=商×除数除数=被除数÷商5、方程的检验过程：检验：方程左边=…… =方程右边所以，x=…是方程的解。

6、列方程解应用题的步骤：（1）弄清题意，找出未知数，用x表示。

（2）分析、找出数量之间的等量关系，列出方程；（3）解方程。

（4）检验，写出答案。

根据倍数关系表示为几x。

再根据两个量的和或差列出方程。

2019-04-081、在含有字母的式子里，数字和字母中间的乘号，字母和字母之间的乘号，可以记作“·”，也可以省略不写。

加号、减号，除号以及数与数之间的乘号不能省略。

2、a×a可以写作a·a或a ，a 读作a的平方。

2a表示a+a3、方程：含有未知数的等式称为方程。

方程一定是等式，但等式不一定是方程。

使方程左右两边相等的未知数的值，叫做方程的解。

求方程的解的过程叫做解方程。

（解方程要先写“解”）方程的解是一个数；解方程是一个计算过程。

4、解方程的原理：（1）等式的基本性质等式左右两边同时加、减、乘、除相同的数（0除外），等式依然成立。

简略方程※用字母表示数在数学中，常常用字母来表示数。

加法互换律： a＋b ＝ b ＋a加法联合律：（a＋b）＋ c＝a＋（ b＋c）乘法互换律： a×b＝b×a乘法联合律：（a×b）× c＝a×（ b×c）乘法分派律：（a＋b）× c ＝ a× c＋ b× c在含有字母的式子里，字母中间的乘号能够记作“·”，也能够省略不写。

乘法互换律： a×b＝b×a →a·b＝b·a 或 ab＝ ba乘法联合律：（a×b）× c＝a×（ b×c）→（a·b）·c＝a·（b·c）或（ab）c＝a（bc）乘法分派律：（a＋b）× c ＝ a× c＋ b× c→（a＋ b）·c ＝a·c＋b·c 或（ a＋b）·c ＝ ac＋bc人们常用字母表示计量单位。

长度单位面积单位质量单位千米km平方千米km2吨t 米m平方米m2千克kg 分米dm平方分米dm2克g 厘米cm平方厘米cm2毫米mm平方毫米mm 2用字母表示正方形的面积和周长用 S 表示面积，用 C 表示周长。

（ 1）假如用 a 表示正方形的边长，那么这个正方形的周长：C =a·4=4a （省略乘号时，一般把数写在字母前方）这个正方形的面积：S =a·a= a2（读作： a 的平方，表示 2 个 a 相乘）（2）假如用 a 表示长方形的长， b 表示宽，那么这个长方形的周长：C =（a+b ）·2=2 （a+b ）这个长方形的面积：S = a b=ab·※解简略方程观点：含有未知数的等式，叫做方程。

（等式不必定是方程，方程必定是等式。

）使方程左右两边相等的未知数的值，叫做方程的解。

简易方程知识点归纳
知识点一、用字母表示数
1、在含有字母的式子中，字母与字母、数字与字母之间的乘号可以记为“.” ，也可以省略不写。

加号、减号、除号不能省略，数字与数字之间的乘号也不能省略。

例：2×a 可以写作2a ；a ×b 可以写作ab ；但2×3不能．．写作2.3，也不能．．
写作23 。

2、如果字母前面的数字是1，则省略这个1。

例：1a 要写成a ；1x 要写成x 。

知识点二、方程的概念
1、含有未知数的等式叫做方程。

2、使方程左右两边相等的未知数的值，叫做方程的解。

求方程的解的过程叫做解方程。

知识点三、天平原理
1、等式的性质1：等式两边加上或减去同一个数，左右两边仍然相等。

2、等式的性质2：等式两边乘以同一个数，或除以同一个不为0的数，左右两边仍然相等。

知识点四、解简易方程的步骤
①去括号
②运用等式的性质，将带有未知数的放在左边，不带未知数的放在右边
③合并
④求出未知数的值
解方程格式的注意事项：①一开始要写上“解”字、②上下的“=”要对齐。

温馨提示：如果时间充裕，解完方程后可以将未知数的值代入原方程进行验算。

知识点五、运用方程解应用题
解题步骤：
①设x来表示未知数。

一般可以设“是”、“比”、“占”后面的量为x，或者“的”字前面的量为x，有时候也可以根据题目问什么，就设什么为x 。

②找出等量关系，列方程。

③解答。