圆曲线主点计算

● 圆曲线方法一：sin (1cos )180i i i i i i x R y R l R ϕϕϕπ⎧⎪=⎪=-⎨⎪︒⎪=⋅⎩——i l 为待定点i P 至起点间的弧长i ϕ为i l 所对的圆心角R 为曲线半径方法二：11802l A R π︒=⋅⋅ 2sin l R A =⋅00cos(/)sin(/)x x l A y y l A =+⋅+-⎧⎨=+⋅+-⎩起点方位角左减右加起点方位角左减右加——00(,)x y 为圆曲线起点坐标方法三：180l A R π︒=⋅ 00cos(/)sin(/)x x R B A y y R B A =+⋅+-⎧⎨=+⋅+-⎩——l 为圆曲线上任意一点距起点距离00(,)x y 为圆曲线圆心坐标B 为圆心到圆曲线起点的方位角，A 为任意点对应的圆心角● 缓和曲线522030406l x l R l ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩——l 为曲线上任一点至起点的曲线长R 曲线半径0l 为缓和曲线全长圆曲线、缓和曲线计算方法1、直线段：先由JD1以及JD2的坐标算出JD1到JD2的方位角，即直线段方位角A ，故可算出HZ 、ZH 坐标及其直线段各点坐标。

2、缓和曲线：以HZ 、ZH 为起点，缓和曲线上任意一点离HZ 、ZH 距离为l ，利用公式522003040()6l x l R l l R ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩为缓和曲线全长,为圆曲线半径算出该点的相对起点坐标，利用arctan y x算出该点相对起点的方位角B ，再根据线路走向及直线段方位角可算出该点的方位角C （顺时针加，逆时针减），用可求出该点相对起点的距离D ，最后用00cos sin x x D C y y D C =+⎧⎨=+⎩可求出该点的坐标。

（00(,)x y 为缓和曲线起点的坐标）3、圆曲线：用上述方法求出圆曲线两端点HY 、YH 坐标，算出HY 到YH 的方位角F ，以及两点间的距离E ，用12arccos ER可算出两端点连线与起点到圆心连线的夹角G ，根据线路走向求出起点到圆心的方位角H （H=F+/-G ），00(,)x y 圆曲线为起点坐标，根据00cos sin x x R H y y R H=+⎧⎨=+⎩，求出圆心坐标。

缓和曲线连同圆曲线的曲线主点测设一、缓和曲线常数计算曲线要素计算前，应进行必要的常数计算。

缓和曲线的常数包括：缓和曲线、切垂距m（切线增长值）、内移距p。

切线角β缓和曲线切线角——过HY（或YH）点的切线与ZH（或HZ）点的切线组成的角。

即，圆曲线被缓和曲线所代替的那一段弧长对应的圆心角。

向切线作垂线的垂足到缓和曲线起点的距离。

切垂距——由圆心O2内移距——加缓和曲线后，圆曲线相对于切线的内移量。

缓和曲线常数按下式计算：二、缓和曲线要素计算、切曲差q。

各曲线要缓和曲线要素包括：切线长T、曲线总长L、外矢距E素按下式计算：式中 L′——HY点到YH点的曲线长。

三、主点里程计算主点里程计算是根据交点里程和缓和曲线要素推算而得，如图4.5.2所示。

铁路习惯推算方法：公路习惯推算方法：四、主点测设方法举例【例4.6.1】已知某线路，交点里程为DK281＋578.59，圆曲线半径R＝500m，转向角α右＝18°22′00″，缓和曲线长l＝40 m。

试计算曲线要素与主点里程。

【解】（1）缓和曲线常数计算：（2）缓和曲线要素计算：（3）主点里程计算：校核：（4）主点测设方法：缓和曲线的圆曲线主点测设与单圆曲线主点测设方法基本相同，ZH、HZ、QZ 的测设方法和精度要求与ZY、YZ、QZ相同。

用直角坐标法（即切线支距法）测设HY、YH点。

如图4.7.1所示，HY、YH点的坐标，按式（4.6.12）、（4.6.13）计算，当l＝l0时，则x、y为：置镜于ZH（HZ）点，后视交点方向，沿视线方向测设x，得HY（HY）点的，得HY（HY）垂足，仪器搬到垂足点，后视切线方向，拨90°角，沿视线测设y点。

一、概述圆曲线是道路、铁路等工程中常见的曲线形式，其设计和计算对工程建设具有重要意义。

在圆曲线中，曲线元素的计算是一项关键工作，而主点里程公式则是计算圆曲线主点里程的重要方法之一。

本文将对圆曲线元素计算和主点里程公式进行介绍和分析。

二、圆曲线元素计算圆曲线的设计和建设需要对其曲率、切线角等曲线元素进行精确的计算。

曲线元素的计算是通过复杂的数学方法和公式进行的，主要包括以下几个步骤：1. 曲率半径的计算圆曲线的曲率半径是曲线的一个重要参数，它反映了曲线的弯曲程度。

曲率半径的计算是通过测量曲线的实际弧长以及曲线的夹角来完成的，具体的计算方法是利用三角函数公式来求解。

2. 切线角的计算在圆曲线的设计中，切线角是一个重要的参量，它可以影响车辆或列车在曲线上行驶时的安全性和稳定性。

切线角的计算是通过测量曲线的实际弧长和曲线的曲率半径来完成的，具体的计算方法同样是利用三角函数公式来求解。

3. 圆曲线上任意点的坐标计算在实际的工程设计中，常常需要知道圆曲线上任意点的坐标，以便进行进一步的设计和施工。

圆曲线上任意点的坐标计算是通过数学方法和几何原理进行的，其中涉及到参数方程、极坐标等数学概念和公式。

三、主点里程公式主点里程是指在道路或铁路设计中，与特定主要参考点（如桥梁、隧道等）相对应的里程值。

在圆曲线设计中，计算主点里程是确保设计和施工准确性的重要步骤。

主点里程的计算可以通过主点里程公式来完成，其具体表达式如下：主点里程 = 基准点里程 + 曲线长度 * （1 + （曲线长度 / 2 * 曲线半径）） / 2在这个公式中，基准点里程是从起始点到基准点的里程值，曲线长度是圆弧的长度，曲线半径是圆曲线的曲率半径。

四、总结圆曲线元素计算和主点里程公式是圆曲线设计中两个重要的计算方法。

通过精确的曲线元素计算和主点里程计算，可以确保圆曲线设计的精准性和可靠性。

在实际工程中，工程师和设计人员需要注意这些计算方法的细节和技巧，以保证工程建设的高质量和安全性。

第二节圆曲线及其主点的测设§11—2 圆曲线及其主点的测设一、圆曲线概述1．圆曲线半径铁路：我国《新建铁路测量工程规范》和《铁路技术管理规程》中规定：采用的圆曲线半径为：4000、3000、2500、2000、1800、1500、1200、1000、800、700、600、550、500、450、400和350米。

各级铁路曲线的最大半径为4000米。

Ⅰ、Ⅱ级铁路的最小半径：在一般地区分别为1000米和800米，在特殊地段为400米；Ⅲ级铁路的最小半径：在一般地区为600米，在特殊困难地区为350米。

公路：我国《公路工程技术标准》中规定：高速公路的最小半径：在平原微丘区为650米,在山岭重丘区为250米；一级公路在上述两种地区分别为400米和125米；二级公路分别为250米和60米；三级公路分别为125米和30米；四级公路分别为60米和15米。

2．圆曲线主点圆曲线的主点：ZY——直圆点, 即直线与圆曲线的分界点；QZ——曲中点,即圆曲线的中点；YZ——圆直点,即圆曲线与直线的分界点。

圆曲线的控制点：ZY、QZ、YZ、JD。

JD——两直线方向的交点,也是一个重要的点,但不在线路上。

图11-3圆曲线及其主点和要素3．圆曲线要素T——切线长,即交点至直圆点或圆直点的直线长度(JD--ZY,JD—YZ之距离)；见图11-3L——曲线长,即圆曲线的长度(ZY—QZ—YZ圆弧的长度）；E0——外矢距,即交点至曲中点的距离(JD至QZ之距离)；α——转向角,即直线方向转变的水平角；R——圆曲线半径。

T、L、E0总称为圆曲线要素.4、圆曲线要素的计算：α和R分别根据实际测定和线路设计时选定，可按公式法或查表法确定圆曲线的要素T、L、E o1）公式法：切线长曲线长外矢距2）查表法：在《铁路曲线测设用表》（以下简称曲线表）中以α、R为引数，查得相应的圆曲线要素。

[例11-1]：已知α=55o43'24"，R=500 m，求圆曲线各要素T，L，E o。

简述单圆曲线主点测设方法
单圆曲线主点测设方法是指通过测量和计算圆曲线上的某些点的位置，来确定圆曲线的主点 (即圆曲线上的最大或最小半径点) 的方法。

以下是单圆曲线主点测设的简要步骤:
1. 测量圆曲线的切线长 L 和斜率 k。

使用圆曲线的切线长和斜率可以计算出圆曲线的切线长偏差值ΔL 和斜率偏差值Δk。

2. 测量圆曲线上任意一点 P(x,y) 的位置，并将其转换为极坐标系中的 (r,θ) 坐标系。

使用圆曲线的参数化表示，可以计算出点 P 的极坐标方程。

3. 计算圆曲线上所有已知点的极坐标方程，并筛选出满足以下条件的
点:r>rmin(即最小半径点) 或 r<rmax(即最大半径点):
- 点 P 的极坐标方程与已知的圆曲线主点坐标方程相同;
- 点 P 的横坐标与已知的圆曲线主点横坐标相等;
- 点 P 的纵坐标与已知的圆曲线主点纵坐标相等。

4. 对于筛选出的所有点 P，计算其到圆心的距离 d 和到切线的距离 d2。

根据圆的性质，距离 d 和 d2 相等且互为相反数。

因此，可以使用以下公式计算点 P 到圆心的距离 d:
d = |d2 - 2r| / (2 - √(2))
其中，r 是点 P 的极坐标方程中的半径。

5. 根据计算出的点 P 到圆心的距离 d，可以使用勾股定理计算出点 P 的坐标 x 和 y。

单圆曲线主点测设方法的应用范围广泛，可以用于各种几何测量和工程测量中。

该方法的主要优点是可以快速测量圆曲线的主点，而且测量结果比较准确。

曲线坐标计算一、圆曲线圆曲线要素：a -------------- 曲线转向角R -------------- 曲线半径根据a及R可以求出以下要素：T --------------- 切线长L -------------- 曲线长E -------------- 外矢距q -------------- 切曲差（两切线长与曲线全长之差）各要素的计算公式为:L R180（弧长）E RRsec 1）2（sec a =cos a 的倒数）圆曲线主点里程：ZY=J[> TQZ=ZY + L/2 或QZ=JD —q /2YZ=QZ + L/2 或YZ=JD + T—qJD=QZ + q/2 （校核用）1、基本知识里程：由线路起点算起，沿线路中线到该中线桩的距离。

表示方法：DK26＋284.56 。

“+”号前为公里数，即26km，“ +”后为米数，即284.56m CK ——表示初测导线的里程。

DK ——表示定测中线的里程。

K ——表示竣工后的连续里程。

铁路和公路计算方法略有不同。

2、曲线点坐标计算（偏角法或弦切角法）已知条件：起点、终点及各交点的坐标。

1）计算ZY、YZ 点坐标通用公式：2）计算曲线点坐标①计算坐标方位角i 点为曲线上任意一点li为i点与ZY点里程之差当曲线左转时用“-”，右转时用“ +”② 计算弦长③ 计算曲线点坐标此时的已知数据为：ZY ( xZY , yZY 、？ZY- i 、C 。

根据坐标正算原理：切线支距法 这种方法是以曲线起点ZY 或终点YZ 为坐标原点，以切线为X 轴，以过原点的半径为丫轴，则圆曲线上任意一点的切线支距坐标可通过以下公式求得： 利用坐标平移和旋转，该点在大地平面直角坐标系中的坐标可由以下公式求得: 式中：a 为ZY(YZ)点沿线路前进方向的切线方位角。

当起点为ZY 时“土”取“ + ”，XO=X(ZY),YO=Y(ZY),曲线为左偏时应以yi=-yi 代入；当起点为YZ 时，“土”取“ -”，XO=X(YZ), YO=Y(YZ), 曲线为左偏时应以yi 二yi 代入；弧长所对的圆心角弦切角弦的方位角注：1、同弧所对的圆周角等于圆心角的一半2、切线性质圆的切线与过切点的半径相垂直3、弦切角定理弦切角等于它所夹弧上的圆周角4、弧长公式由L/ n R=n /180 °得L=n°n R/ 180 °=n n R/180二、缓和曲线(回旋线)缓和曲线主要有以下几类：A:对称完整缓和曲线(基本形)------切线长、Is1与ls2都相等。

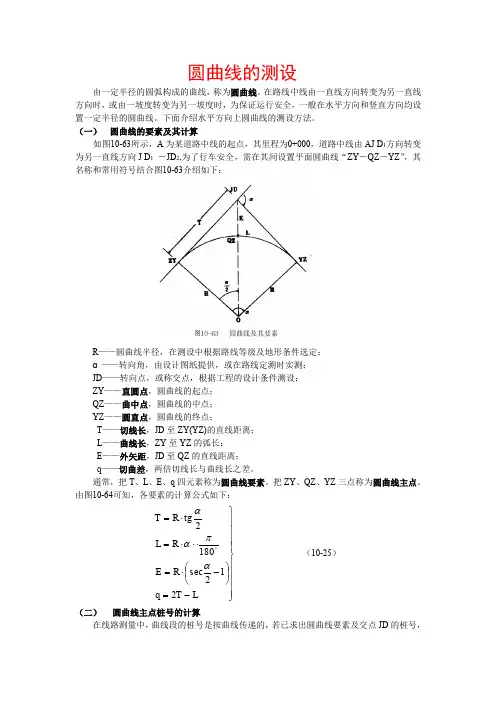
圆曲线的测设由一定半径的圆弧构成的曲线，称为圆曲线。

在路线中线由一直线方向转变为另一直线方向时，或由一坡度转变为另一坡度时，为保证运行安全，一般在水平方向和竖直方向均设置一定半径的圆曲线。

下面介绍水平方向上圆曲线的测设方法。

（一） 圆曲线的要素及其计算如图10-63所示，A 为某道路中线的起点，其里程为0+000，道路中线由AJ D 1方向转变为另一直线方向J D 1 －JD 2,为了行车安全，需在其间设置平面圆曲线“ZY －QZ －YZ ”，其名称和常用符号结合图10-63介绍如下：R ——圆曲线半径，在测设中根据路线等级及地形条件选定；α——转向角，由设计图纸提供，或在路线定测时实测；JD ——转向点，或称交点，根据工程的设计条件测设；ZY ——直圆点，圆曲线的起点；QZ ——曲中点，圆曲线的中点；YZ ——圆直点，圆曲线的终点；T ——切线长，JD 至ZY(YZ)的直线距离；L ——曲线长，ZY 至YZ 的弧长；E ——外矢距，JD 至QZ 的直线距离；q ——切曲差，两倍切线长与曲线长之差。

通常，把T 、L 、E 、q 四元素称为圆曲线要素。

把ZY 、QZ 、YZ 三点称为圆曲线主点。

由图10-64可知，各要素的计算公式如下：⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫-=⎪⎭⎫ ⎝⎛-⋅=⋅⋅⋅=⋅=︒L T q R E R L tg R T 212sec 1802απαα （10-25）（二） 圆曲线主点桩号的计算在线路测量中，曲线段的桩号是按曲线传递的，若已求出圆曲线要素及交点JD 的桩号，则计算圆曲线主点桩号的一般公式如下：⎪⎪⎪⎭⎪⎪⎪⎬⎫+=+=-=22L QZ YZ L ZY QZ T JD ZY 桩号桩号桩号桩号桩号桩号 （10-26） 主点桩号的检核，可用切曲差q 来验算，其公式为：q T JD YZ -+=桩号桩号（三） 圆曲线主点的放样方法求出圆曲线要素之后，可按下述步骤测设圆曲线主点：1. 将经纬仪安置于交点J D 1上（见图10-63），分别瞄准起点A 和交点J D 2，从J D 1起沿切线方向用钢尺测设切线长T ，在地面上分别标定出曲线起点ZY 和曲线终点YZ 。

圆曲线要素及计算公式前言《礼记》有云：大学之道，在明德，在亲民。

在提笔撰写我的毕业设计论文的时候，我也在向我的大学生活做最后的告别仪式。

我不清楚过去的一切留给现在的我一些什么，也无从知晓未来将赋予我什么，但只要流泪流汗，拼过闯过，人生才会少些遗憾！非常幸运能够加入水利工程这个古老而又新兴的行业，即将走向工作岗位的时刻，我仿佛感受到水利行业对我赋予新的历史使命，水利是一项以除害兴利、趋利避害，协调人与水、人与大自然关系的高尚事业。

水利工作，既要防止水对人的侵害，更要防止人对水的侵害；既要化解自然灾害对人类生命财产的威胁，又要善待自然、善待江河、善待水，促进人水和谐，实现人与自然和谐相处。

这种使命，更让我用课堂中的知识用于实际生产中来。

特别是这两个月来的毕业设计，我越发感觉到学会学精测量基础知识对于我贡献水利是多么的重要。

所以，我越发不愿放弃不多的大学时光，努力提高自己的实践动手能力，而本学期的毕业设计，为我提供了绝好的机会，我又怎能放弃？刚刚从老师那里得到毕业设计的题目和任务时，我的心里真的没底。

作为毕业设计的主体工作，我们主要运用电子水准仪对某幢建筑物进行变形观测与计算，布设控制点进行平面控制测量和高程控制测量；用全站仪进行了中心多边行角度和距离的测量，并用条件平差原理进行平差，通过控制点的放样来计算土的挖方量，还有圆曲线的计算与测设。

而我研究的毕业课题是圆曲线测设。

大学的最后一个学期过得特别快，几乎每天扛着仪器，奔走在校园的每个角落，生活亦很有节奏。

今天我提笔写毕业论文，我的毕业设计也接近尾声。

不管成果如何，毕竟心里不再是没底了，挑着两个多月的辛苦换来的数据和成果，并不断的完善他们，心里感觉踏实多了。

在本次毕业设计论文的设计中要感谢水利系为我们的工作提供了测量仪器，还有各指导老师的教导和同学的帮助。

摘要：在公路、铁路的路线圆曲线测设中，一般是在测设出曲线各主点后，随之在直圆点或圆直点进行圆曲线详细测设。

前?????言《礼记》有云：大学之道，在明德，在亲民。

在提笔撰写我的毕业设计论文的时候，我也在向我的大学生活做最后的告别仪式。

我不清楚过去的一切留给现在的我一些什么，也无从知晓未来将赋予我什么，但只要流泪流汗，拼过闯过，人生才会少些遗憾！非常幸运能够加入水利工程这个古老而又新兴的行业，即将走向工作岗位的时刻，我仿佛感受到水利行业对我赋予新的历史使命，水利是一项以除害兴利、趋利避害，协调人与水、人与大自然关系的高尚事业。

水利工作，既要防止水对人的侵害，更要防止人对水的侵害；既要化解自然灾害对人类生命财产的威胁，又要善待自然、善待江河、善待水，促进人水和谐，实现人与自然和谐相处。

这种使命，更让我用课堂中的知识用于实际生产中来。

特别是这两个月来的毕业设计，我越发感觉到学会学精测量基础知识对于我贡献水利是多么的重要。

所以，我越发不愿放弃不多的大学时光，努力提高自己的实践动手能力，而本学期的毕业设计，为我提供了绝好的机会，我又怎能放弃？刚刚从老师那里得到毕业设计的题目和任务时，我的心里真的没底。

作为毕业设计的主体工作，我们主要运用电子水准仪对某幢建筑物进行变形观测与计算，布设控制点进行平面控制测量和高程控制测量；用全站仪进行了中心多边行角度和距离的测量，并用条件平差原理进行平差，通过控制点的放样来计算土的挖方量，还有圆曲线的计算与测设。

而我研究的毕业课题是圆曲线测设。

大学的最后一个学期过得特别快，几乎每天扛着仪器，奔走在校园的每个角落，生活亦很有节奏。

今天我提笔写毕业论文，我的毕业设计也接近尾声。

不管成果如何，毕竟心里不再是没底了，挑着两个多月的辛苦换来的数据和成果，并不断的完善他们，心里感觉踏实多了。

在本次毕业设计论文的设计中要感谢水利系为我们的工作提供了测量仪器，还有各指导老师的教导和同学的帮助。

?摘??要：在公路、铁路的路线圆曲线测设中，一般是在测设出曲线各主点后，随之在直圆点或圆直点进行圆曲线详细测设。